Swing-by: Unterschied zwischen den Versionen

Breaking News
Zufallsbild: daulon / DepositPhotos

Swing-by: Unterschied zwischen den Versionen

imported>FranzR
(2 tote Links wiederbelebt u. a.)
 
imported>M Huhn
K (Relativsatz)
 
Zeile 1: Zeile 1:
{{Lückenhaft|* Das Thema sollte besser veranschaulicht werden.
[[Datei:Swingbyvxy.png|mini|Swing-by mit Ablenkung des Flug­körpers um 180° und 90°. Seine Geschwindig­keit relativ zum Planeten (blauer Pfeil) bleibt im Betrag gleich. Durch vektorielle Addition der Geschwindig­keit des Planeten relativ zur Sonne (gelber Pfeil) erhält man die Geschwindig­keit des Flug­körpers relativ zur Sonne (grauer Pfeil).]]
* Siehe: [[Diskussion:Swing-by#Markierung Lückenhaft|Diskussion:Swing-by]]}}
Der englische Begriff '''Swing-by''' – auch '''Slingshot, Gravity-Assist''' (GA), '''Schwerkraftumlenkung''' oder '''Vorbeischwungmanöver''' genannt – bezeichnet eine Methode der [[Raumfahrt]], bei der ein relativ leichter Raumflugkörper (etwa eine [[Raumsonde]]) dicht an einem sehr viel größeren Körper (etwa einem [[Planet]]en) vorbeifliegt. Bei dieser Variante eines [[Vorbeiflug (Raumfahrt)|Vorbeiflugs]] wird die Flugrichtung der Sonde verändert, wobei auch deren Geschwindigkeit gesteigert oder gemindert werden kann. Ein Swing-by-Manöver kann auch mit einer Triebwerkszündung kombiniert werden. Bei sehr nahen Vorbeiflügen kann unter Umständen eine deutlich höhere Effizienz des Treibstoffs erreicht werden ([[Oberth-Effekt]]).


Der englische Begriff '''Swing-by''' – auch '''Slingshot, Gravity-Assist''' (GA), '''Schwerkraftumlenkung, Gravitationsmanöver''' oder '''Vorbeischwungmanöver''' genannt – bezeichnet eine Methode der [[Raumfahrt]], bei der ein relativ leichter Raumflugkörper (etwa eine [[Raumsonde]]) dicht an einem sehr viel größeren Körper (etwa einem [[Planet]]en) vorbeifliegt. Bei dieser Variante eines [[Vorbeiflug (Raumfahrt)|Vorbeiflugs]] wird die Flugrichtung der Sonde verändert, wobei auch deren Geschwindigkeit gesteigert oder gemindert werden kann. Die Bahn des Planeten wird wegen seiner deutlich größeren Masse nicht merklich verändert. Ein Swing-by-Manöver kann auch mit einer Triebwerkszündung kombiniert werden. Bei sehr nahen Vorbeiflügen kann unter Umständen eine deutlich höhere Effizienz des Treibstoffs erreicht werden (siehe [[Oberth Effect]]).
Der Swing-by-Effekt tritt auch auf, wenn ein Komet, ein Asteroid oder (wie es vermutlich in der frühen Geschichte des Sonnensystems geschah) ein leichterer Planet einen schwereren Planeten in dessen Gravitationsfeld passiert. Wenn die Masse des leichteren Planeten gegenüber dem schwereren nicht vernachlässigbar klein ist, ändert auch der schwerere Planet seine Sonnenumlaufbahn merklich.<ref name="astronews">{{Internetquelle |url=http://www.astronews.com/news/artikel/2011/11/1111-023.shtml |titel=Sonnensystem. Gab es einst fünf Gasriesen? |autor=Stefan Deiters |hrsg=astronews.com |datum=2011-11-16 |zugriff=2014-04-16}}</ref><ref name="suw">{{Internetquelle |url=http://www.sterne-und-weltraum.de/news/der-verstossene-planet/1129062 |titel=Sonnensystem. Der verstoßene Planet |autor=Laura Hennemann |hrsg=sterne-und-weltraum.de |datum=2011-11-15 |zugriff=2014-04-16}} (Der Artikel nennt als Quelle: {{arXiv|1109.2949}})</ref>
 
Der Swing-by-Effekt tritt auch auf, wenn ein leichterer Planet oder ein Asteroid einen schwereren Planeten in dessen Gravitationsfeld passiert. Wenn jedoch die Masse des leichteren Planeten gegenüber dem schwereren nicht vernachlässigbar klein ist, ändert auch der schwerere Planet seine Sonnenumlaufbahn merklich.<ref name="astronews">{{Internetquelle |url=http://www.astronews.com/news/artikel/2011/11/1111-023.shtml |titel=Sonnensystem. Gab es einst fünf Gasriesen? |autor=Stefan Deiters |hrsg=astronews.com |datum=2011-11-16 |zugriff=2014-04-16}}</ref><ref name="suw">{{Internetquelle |url=http://www.sterne-und-weltraum.de/news/der-verstossene-planet/1129062 |titel=Sonnensystem. Der verstoßene Planet |autor=Laura Hennemann |hrsg=sterne-und-weltraum.de |datum=2011-11-15 |zugriff=2014-04-16}} (Der Artikel nennt als Quelle: {{arxiv|1109.2949}})</ref>


== Prinzip ==
== Prinzip ==
Fliegt eine Sonde durch das [[Gravitationsfeld]] eines Planeten, wird sie durch dessen Anziehungskraft abgelenkt und erfährt eine Geschwindigkeitsänderung in dem Bezugssystem, das zur Beschreibung der Planetenbewegung verwendet wird. Je nachdem, ob die Sonde vor oder hinter dem Planeten seine Umlaufbahn überquert, verringert oder erhöht sich ihre Geschwindigkeit in diesem Bezugssystem.
<gallery widths="240" heights="180" class="float-right" caption="Zeitlicher Verlauf der Geschwindigkeit beim Swing-By">
 
Swingby acc anim.gif|Swing-by, um Geschwindigkeit aufzunehmen
Aus Sicht des Planeten wird die Sonde nicht beschleunigt oder gebremst, sondern nur abgelenkt. Der Planet bewegt sich aber auch um die Sonne. Deshalb wurde die Geschwindigkeit der Sonde aus Sicht der Sonne verändert.
Swingby dec anim.gif|Swing-by, um Geschwindigkeit abzubauen
 
</gallery>
[[Datei:Swingbyvxy.png|ohne|gerahmt|Die 1. und 2. Darstellung zeigt einen tangentialen Anflug. Die 3. und 4. Darstellung zeigt als Grenzfall einen radialen Anflug von der Sonne (hier als y-Richtung) und einen tangentialen Abflug zur Planetenbahn. Das relativ kurzzeitige Manöver erlaubt eine Vernachlässigung der Krümmung der Planetenbahn. Die 3. und 4. Darstellung zeigt, dass eine Umlenkung der [[Impuls]]- bzw. Geschwindigkeitskomponente von y letztendlich zu einer Addition oder Subtraktion mit der x-Komponenten führt. So wird die Sonde im Ergebnis schneller oder langsamer. Alle Vorgänge können in der Zeit auch umgekehrt werden, womit sich die jeweilige Wirkung ebenfalls ändert.]]
Bewegt sich eine Sonde durch das [[Gravitationsfeld]] eines Planeten, wird sie durch dessen Anziehungskraft abgelenkt. ''Bezogen auf den Planeten'' verändert sich der Betrag der Geschwindigkeit der Sonde in unendlicher Entfernung zum Planeten ''nicht'', d.&nbsp;h. die Bahnenergie des Raumfahrzeugs bezogen auf den Planeten bleibt konstant. Nur die Richtung der Geschwindigkeit wird durch die Ablenkung verändert.  


=== Fehler der vereinfachten Darstellung ===
Hinzu kommt aber, dass sich der Planet um die Sonne bewegt. Die Geschwindigkeit der Sonde relativ zur Sonne ist die vektorielle Summe der Geschwindigkeit der Sonde relativ zum Planeten und der Geschwindigkeit des Planeten um die Sonne, und diese Summe ändert sich im Betrag. ''Bezogen auf die Sonne'' wird die Sonde somit schneller oder langsamer. Anders ausgedrückt: Die Gravitationskräfte zwischen Sonde und Planeten koppeln die beiden Bewegungen miteinander und ermöglichen einen Austausch von Bahnenergie zwischen beiden.  
Es gelten die Erhaltungssätze für [[Energieerhaltungssatz|Energie]] und [[Impulserhaltungssatz|Impuls]]. Da keine [[Kinetische Energie|Bewegungsenergie]] entsteht, sondern der Planet einen kleinen Teil seiner Bewegungsenergie zur Sonde überträgt (oder umgekehrt), wird die Bahn des Planeten auch verändert, allerdings nur unmerklich, da der Planet eine sehr viel höhere Masse als die Sonde hat.


Das Gravitationsfeld des Planeten reicht außerdem unendlich weit und kann deshalb nie verlassen werden. Mit steigendem Abstand zum Planeten wird aber dessen Anziehungskraft so gering, dass irgendwann die Anziehungskraft der Sonne entscheidender ist und die Sonde sich in einem Orbit um die Sonne befindet.
=== Auswirkungen ===
Grundsätzlich ergeben sich die folgenden Auswirkungen:
* Änderung des Geschwindigkeitbetrages im übergeordneten Bezugssystem, d.&nbsp;h. der Bahnenergie des Raumfahrzeugs
* Änderung der Flugrichtung innerhalb der Bahnebene des Bezugsystems (z.&nbsp;B. der [[Ekliptik]]) zum Anvisieren neuer Ziele
* Änderung der Bahnebene, z.&nbsp;B. Verlassen der Ekliptik


Die Einflüsse weiterer Körper und relativistischer Effekte wurden der Einfachheit halber ebenfalls vernachlässigt.
Aufgrund der erheblich größeren Masse des Planeten verglichen mit dem Raumfahrzeug sind die Auswirkungen auf die Planetenbahn nicht messbar, während die Bahnenergie der Sonde sich erheblich verändern kann.


== Vergleich mit Stoßvorgängen ==
Swing-by-Manöver können damit auf [[Interplanetarer Raum|interplanetaren]] Flügen zur Einsparung von Treibstoff dienen und daher auch Kosten reduzieren. Die Reisezeit kann durch die gewonnene Geschwindigkeit verkürzt werden, infolge von Umwegen aber auch steigen. Am Zielplaneten kann mit Swing-by an einem Trabanten (Mond) die Reisegeschwindigkeit abgebaut werden, um die Sonde in eine Umlaufbahn zu bringen.
Vereinfachend kann zur Veranschaulichung auch der [[Elastischer Stoß|elastische Stoß]] zweier Körper herangezogen werden.<ref name="jpl">{{Internetquelle |url=http://www2.jpl.nasa.gov/basics/grav/primer.php |titel=A Gravity Assist Primer |hrsg=JPL/NASA |zugriff=2014-04-16 |sprache=en |archiv-datum=2016-07-26 |archiv-url=http://web.archive.org/web/20160726045127/http://solarsystem.nasa.gov/basics/grav/primer.php}}</ref> Der Vergleich mit praxisnahen Stoßvorgängen zweier Körper ist allerdings nur möglich, wenn man bei diesen und beim Swing-by-Manöver Reibungsfreiheit voraussetzt und die Betrachtung auf die Beträge und Richtungen der Geschwindigkeiten unmittelbar vor und nach dem Vorgang beschränkt. Dabei müssen beim Swing-by die Vergleichspositionen auch noch im gleichen Abstand zum Planeten in dessen Bezugssystem sein.


Ohne diese Reduktion spielt z.&nbsp;B. beim Tischtennis zusätzlich die Reibung mit dem Schläger und mit der Luft ([[Magnus-Effekt]]) eine große Rolle. Auch beim Swing-by müssen zu diesem Vergleich Brems- oder Schubmanöver unterlassen werden. Der Winkel zwischen An- und Abflug wird beim Swing-by durch Geschwindigkeit und Annäherung bestimmt, dagegen beim Tischtennis durch den Anstellwinkel des Schlägers. Die durchgehenden Bahnformen beim Swing-by mit zwei Körpern folgen den [[Keplersche Gesetze|Keplerschen Gesetzen]], beim Tischtennis dagegen der [[Ballistik]].
=== Vergleich mit Stoßvorgängen ===
[[Datei:Swingbyvxytt.png|ohne|gerahmt|Fallbeispiele, abgeleitet für den Vergleich mit den Beispielen zum Swing-by-Manöver. Der gepunktete Körper beschreibt den Zustand nach dem Stoß mit der Geschwindigkeit v<sub>2</sub>.]]
Vereinfachend kann zur Veranschaulichung der [[Elastischer Stoß|elastische Stoß]] zweier Körper herangezogen werden,<ref name="jpl">{{Internetquelle |url=http://www2.jpl.nasa.gov/basics/grav/primer.php |titel=A Gravity Assist Primer |hrsg=JPL/NASA |zugriff=2014-04-16 |sprache=en |archiv-datum=2016-07-26 |archiv-url=http://web.archive.org/web/20160726045127/http://solarsystem.nasa.gov/basics/grav/primer.php}}</ref> beispielsweise der frontale Kontakt eines Tischtennisballs mit einem Tischtennis&shy;schläger. Wenn der Tischtennis&shy;schläger unbeweglich ruht, prallt der Ball idealisiert (also ohne Berücksichtigung von Reibung) mit gleicher Geschwindigkeit wieder ab. Bewegt der Spieler den Schläger dem Ball entgegen, prallt dieser (aus Sicht des Zuschauers) mit höherer Geschwindigkeit zurück; umgekehrt kann der Spieler durch „Zurücknehmen“ des Schlägers den Ball abbremsen. Aus „Sicht“ (Inertialsystem) des Schlägers prallt er stets mit gleicher Geschwindigkeit zurück, sonst wäre es kein elastischer Stoß.
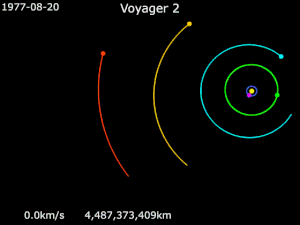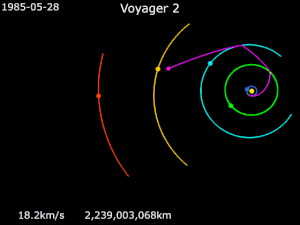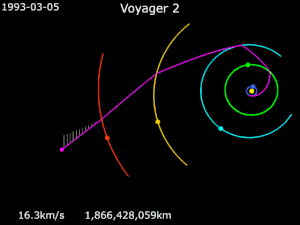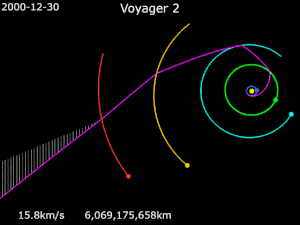
[[Datei:Animation of Voyager 2 trajectory.gif|mini|Trajektorie von Voyager&nbsp;2
{| width="100%"
|-
| style="vertical-align:top;" width="50%" | {{Farblegende|#ff00ff|[[Voyager 2]]|}}{{Farblegende|#ffff00|[[Sonne]]|}}{{Farblegende|#1e90ff|[[Erde]]|}}{{Farblegende|#00ff00|[[Jupiter (Planet)|Jupiter]]|}}
| style="vertical-align:top" | {{Farblegende|#00ffff|[[Saturn (Planet)|Saturn]]|}}{{Farblegende|#ffcc00|[[Uranus (Planet)|Uranus]]|}}{{Farblegende|#ff0000|[[Neptun (Planet)|Neptun]]|}}
|}
]]
Wenn sich Ball und Schläger nicht frontal treffen, muss noch die seitliche Geschwindigkeits&shy;komponente berücksichtigt werden; ebenso ist es beim Swing-by, da die Raumsonde nicht frontal auf den Planeten trifft. Beim Swing-by findet die Wechselwirkung über einen längeren Zeitraum statt, aber das Grundprinzip ist gleich.


== Wirkungen ==
=== Routenplanung ===
Grundsätzlich ergeben sich die folgenden Wirkungen:
Da es sich in der Realität mindestens um ein [[Dreikörperproblem]] handelt (z.&nbsp;B. Sonde, Planet und Sonne), sind die Bahnänderungen nicht analytisch, sondern nur [[Numerische Mathematik|numerisch]] genauer zu berechnen. Da der Flugwinkel und die Geschwindigkeit nach der Passage voneinander abhängen, ist der Spielraum für die Entfernung und die Position des nächsten Zielobjektes begrenzt. Bei Vorgabe mehrerer Ziele und/oder Einschränkung auf eine bestimmte Anflugbahn und Geschwindigkeit beim Ziel entsteht ein Gleichungssystem, das numerisch auf Lösungen überprüft wird. Die Lösungen ([[Trajektorie (Physik)|Trajektorien]]) ergeben zumeist nur schmale Startzeitfenster in der Größenordnung von Tagen oder Wochen, die für die gleichen Missionsziele Jahre oder viele Jahrzehnte auseinander liegen können. Die Startgeschwindigkeit von der Erde und damit die Kosten der Raketen, sowie die Dauer der Mission sind ebenfalls Vorgaben oder Ergebnisse der Berechnungen.
* Änderung der Geschwindigkeit, z.&nbsp;B. für sonnennähere Ziele als die Venus, oder fernere Ziele als der Mars
* Änderung der Flugrichtung innerhalb der Bahnebene der Ekliptik zum Anvisieren neuer Ziele
* Änderung der Bahnebene, d.&nbsp;h. Verlassen der [[Ekliptik]]
Swing-by-Manöver können damit auf [[Interplanetarer Raum|interplanetaren]] Flügen zur Einsparung von Treibstoff dienen und daher auch Kosten reduzieren. Die Reisezeit kann durch die gewonnene Geschwindigkeit verkürzt werden, infolge von Umwegen aber auch steigen. Am Zielplaneten kann mit Swing-by an einem Begleiter (Mond) die Reisegeschwindigkeit abgebaut werden, um die Sonde in eine Umlaufbahn zu bringen.


== Routenplanung ==
Der [[Tisserandparameter]] wird bei der Planung von Gravity-Assists verwendet, um mögliche Partnerkörper zu finden. Es handelt sich um eine näherungsweise Erhaltungsgröße, welche sich aus verschiedenen geometrischen Bahnparametern ergibt und vor und nach einem Gravity-Assist ungefähr gleich ist. Somit ergibt sich eine Einschränkung, welche Bahn überhaupt möglich ist.<ref name="miller_weeks">{{Internetquelle |url=https://arc.aiaa.org/doi/abs/10.2514/6.2002-4717 |titel=Application of Tisserand's Criterion to the Design of Gravity Assist Trajectories |autor=James Miller & Connie Weeks |hrsg=AIAA |werk=AIAA/AAAS Astrodynamics Specialist Conference |datum= 2002 |archiv-url= |archiv-datum= |zugriff=2022-12-15 |sprache=en |format=PDF |offline=}}</ref>
Da es sich in der Realität mindestens um ein [[Dreikörperproblem]] handelt (z.&nbsp;B. Sonde, Planet und Sonne), sind die Bahnänderungen nicht analytisch, sondern nur numerisch genauer zu berechnen. Da der Flugwinkel und die Geschwindigkeit nach der Passage voneinander abhängen, ist der Spielraum für die Entfernung und die Position des nächsten Zielobjektes begrenzt. Bei Vorgabe mehrere Ziele und/oder Einschränkung auf eine bestimmte Anflugbahn und Geschwindigkeit beim Ziel entsteht ein Gleichungssystem, das numerisch auf Lösungen überprüft wird. Die Lösungen ([[Trajektorie (Physik)|Trajektorien]]) ergeben zumeist nur schmale Startzeitfenster in der Größenordnung von Tagen oder Wochen, die für die gleichen Missionsziele Jahre oder viele Jahrzehnte auseinander liegen können. Die Startgeschwindigkeit von der Erde und damit die Kosten der Raketen, sowie die Dauer der Mission sind ebenfalls Vorgaben oder Ergebnisse der Berechnungen.


== Geschichte ==
== Geschichte ==
Die Bedeutung der Swing-by-Manöver für die Raumfahrt wurde 1961 von [[Michael Minovitch]] entdeckt und am [[Jet Propulsion Laboratory]] untersucht.<ref>M. Minovitch: ''[http://www.gravityassist.com/ Gravity Assist.]''</ref> Das erste Swing-by-Manöver wurde 1970 während der [[Apollo 13|Apollo-13-Mission]] durchgeführt. Die Besatzung konnte sich nach der Explosion eines Sauerstofftanks durch ein Swing-by-Manöver um den Mond wieder zurück zur Erde retten. Im Februar 1974 war [[Mariner]]&nbsp;10 die erste Raumsonde, die ein Swing-by-Manöver an einem anderen Planeten durchführte, sie wurde durch den Vorbeiflug an der [[Venus (Planet)|Venus]] genügend abgebremst, um den Planeten [[Merkur (Planet)|Merkur]] zu erreichen. Dadurch konnte einerseits die Raumsonde mit einer (gegenüber der [[Titan (Rakete)|Titan&nbsp;IIIC]]) preiswerteren [[Atlas (Rakete)|Atlas-Centaur]] gestartet und andererseits die Venus mitbesucht werden.<ref>''[http://history.nasa.gov/SP-424/ch2.htm SP-424 Mariner Venus-Mercury Mission.]'' Bei: ''History.NASA.gov.''</ref> Heute nutzen nahezu alle interplanetaren Raumsonden, die nicht den [[Mars (Planet)|Mars]] oder die Venus zum Endziel haben, diese Technik.
[[Datei:Voyager 2 Heliocentric Velocity.png|mini|Geschwindigkeits&shy;profil der Sonde Voyager 2. Erst durch Swing-by am Jupiter konnte die Flucht&shy;geschwindig&shy;keit aus dem Sonnen&shy;system ''(solar escape velocity)'' erreicht werden. Weiterer Geschwin&shy;digkeits&shy;zuwachs erfolgte an Saturn und Uranus. Am Neptun wurde die Sonde nahe an dessen Mond Triton geführt; dabei wurde Geschwin&shy;digkeits&shy;verlust in Kauf genommen.]]
 
Swing-by-Manöver zur Änderung der Flugrichtung fanden schon in der Frühzeit der Raumfahrt statt, so bei der Sonde [[Lunik 3|Luna&nbsp;3]] (1959), die als erste den Mond umrundete und wieder Kurs auf die Erde nahm.<ref name="luna3">{{Internetquelle |url=http://www.planetary.org/multimedia/space-images/charts/luna-3-orbit.html |titel=Luna 3 orbit |autor= |hrsg=The Planetary Society |werk= |datum= |archiv-url= |archiv-datum= |zugriff=2018-12-17 |format= |offline=}}</ref> Auch bei [[Apollo 13|Apollo&nbsp;13]] (1970) wurde ein Swing-by-Manöver verwendet, um den Mond in einer Schleife zu umfliegen und direkt zurückzukehren.<ref>{{Literatur |Autor=W. David Woods |Titel=How Apollo Flew to the Moon |Verlag=Springer |Datum= |Online={{Google Buch |BuchID=x-taL4N0sjIC |Seite=125 |Hervorhebung=free-return}}}}</ref> Bei der Sonnensonde [[Ulysses (Sonde)|Ulysses]] (1990) wurde ein Swing-by am Jupiter dazu genutzt, die [[Bahnneigung|Inklination]] zu ändern, um die Ebene der Ekliptik zu verlassen.
== Beispiele ==
Die [[Voyager-Sonden]] verwendeten zielgerichtet alle Wirkungen in mehreren Swing-by-Manövern zur Erkundung der äußeren Planeten. So sparten sie Treibstoff beim Start, bzw. verkürzten die Missionszeit durch den Beschleunigungseffekt beginnend beim Jupiter. Durch die Änderung der Flugrichtung steuerten sie einen äußeren Planeten nach dem anderen an (Grand Tour). Durch das Swing-by am Saturn erreichten die Sonden die [[Kosmische Geschwindigkeit#Dritte kosmische Geschwindigkeit|dritte kosmische Geschwindigkeit]]. Ohne Swing-by hätte [[Voyager 2|Voyager&nbsp;2]] mehr als doppelt so lange gebraucht, um [[Neptun (Planet)|Neptun]] zu erreichen.
Die Änderung der Bahnebene brachte Voyager 1 näher an den Saturnmond Titan. Mit der Ablenkung aus der Ekliptik fand sich aber nun kein anderer Himmelskörper zur Umkehr per Swing-by-Manöver.


[[Datei:Cassini interplanetary trajectory DE.svg|mini|Flugbahn der [[NASA]]/[[ESA]]-[[Raumsonde]] [[Cassini-Huygens]]: Nach dem Start von der Erde flog sie zweimal an der [[Venus (Planet)|Venus]], einmal an der [[Erde]] und einmal am [[Jupiter (Planet)|Jupiter]] vorbei, bis sie durch diese Swing-by-Manöver genug [[kinetische Energie]] hatte, ihr Ziel, den [[Saturn (Planet)|Saturn]], erreichen zu können.]]
Dass man Raumsonden durch Swing-by zusätzliche Geschwindigkeit verleihen kann, entdeckte 1961 [[Michael Minovitch]], der am [[Jet Propulsion Laboratory]] arbeitete.<ref>M. Minovitch: ''[http://www.gravityassist.com/ Gravity Assist.]''</ref><ref name="histsurvey" /> Zuvor hatte es als ausgeschlossen gegolten, dass man jemals mit konventioneller Raketentechnik die Planeten des äußeren Sonnensystems erreichen könnte. Der Grund dafür ist das theoretisch angenommene energetische Minimum, das durch einen [[Hohmann-Transfer]] gegeben ist,<ref name="histsurvey">{{Internetquelle |url=http://www.gravityassist.com/IAF3-1/revisions083010/IAF3Pub.pdf |titel=The Effect of Gravity-Propelled Interplanetary Space Travel on the Exploration of the Solar System: Historical Survey, 1961 to 2000 |autor=Richard L. Dowling et al |hrsg=Donald C Elder |werk=History of Rocketry and Astronautics, AAS History Series, Vol 28 |seiten=339 |datum= |archiv-url= |archiv-datum= |zugriff=2018-12-17 |sprache=en |format=PDF |offline=}}</ref><ref>{{Literatur |Autor=Reiner Klingholz |Titel=Marathon im All: die einzigartige Reise der Voyager 2 |Auflage= |Verlag=Ullstein |Ort= |Datum=1992 |ISBN=3-548-34870-X |Seiten=23}}</ref> und die Tatsache, dass nach der [[Raketengrundgleichung]] die erforderliche Startmasse des Raumfahrzeugs exponentiell mit der benötigten Endgeschwindigkeit wächst.


Bei Mondmissionen wurden Swing-by-Manöver verwendet, um den Mond in einer Schleife zu umfliegen.<ref>{{Literatur |Titel=How Apollo Flew to the Moon |Autor=W. David Woods |Verlag=Springer |Online={{Google Buch |BuchID=x-taL4N0sjIC |Seite=125 |Hervorhebung=free-return}}}}</ref>
Die ersten interplanetaren Sonden, die diese Technik nutzten, waren [[Pioneer 10|Pioneer&nbsp;10]] (1972: Erde → [[Jupiter (Planet)|Jupiter]] → interstellarer Raum), [[Pioneer 11|Pioneer&nbsp;11]] (1973: Erde → Jupiter → [[Saturn (Planet)|Saturn]] → interstellarer Raum) und [[Mariner 10|Mariner&nbsp;10]] (1973: Erde → [[Venus (Planet)|Venus]] → [[Merkur (Planet)|Merkur]])<ref>''[http://history.nasa.gov/SP-424/ch2.htm SP-424 Mariner Venus-Mercury Mission.]'' Bei: ''History.NASA.gov.''</ref>. Von besonderer Bedeutung wurde Swing-by für die beiden [[Voyager-Programm|Voyager-Sonden]] (1977): Aufgrund einer Planetenkonstellation, wie sie nur alle 176 Jahre vorkommt, konnte [[Voyager 2|Voyager&nbsp;2]] nacheinander die Planeten Jupiter, Saturn, [[Uranus (Planet)|Uranus]] und [[Neptun (Planet)|Neptun]] besuchen und dabei, ebenso wie ihre Schwestersonde [[Voyager 1|Voyager&nbsp;1]], die Jupiter und Saturn besuchte, die [[Kosmische Geschwindigkeit#Dritte kosmische Geschwindigkeit|dritte kosmische Geschwindigkeit]] erreichen, die sie in den interstellaren Raum brachte.


Häufig werden Swing-bys nicht verwendet, um die Reisezeit zu verkürzen, sondern um Raumsonden mit Trägerraketen zu starten, die für den direkten Flug zum Ziel zu schwach sind. Um dennoch zum Ziel zu kommen, muss dann die Raumsonde einen oder mehrere Swing-bys durchführen, um die nötige Geschwindigkeit zu erreichen. Dadurch wird die Flugzeit deutlich länger als bei einem direkten Flug. Meistens ist der Grund für dieses Vorgehen, dass eine größere Trägerrakete teurer wäre als die längere Missionszeit. Nur manchmal, wie z.&nbsp;B. bei [[Cassini-Huygens]], ist die Sonde so schwer, dass selbst die größte Trägerrakete nicht für einen Direktflug reicht.
[[Datei:Cassini interplanetary trajectory DE.svg|mini|Flugbahn der [[NASA]]/[[ESA]]-[[Raumsonde]] [[Cassini-Huygens]]: Nach dem Start von der Erde flog sie zweimal an der [[Venus (Planet)|Venus]], einmal an der Erde und einmal am [[Jupiter (Planet)|Jupiter]] vorbei, bis sie durch diese Swing-by-Manöver genug [[kinetische Energie]] hatte, ihr Ziel, den [[Saturn (Planet)|Saturn]], erreichen zu können.]]


Besonders beim zweiten Grund entstehen große Umwege. So wurde zum Beispiel die Sonde Cassini-Huygens auf dem Weg zum [[Saturn (Planet)|Saturn]] zuerst zweimal von der [[Venus (Planet)|Venus]] und dann einmal von der Erde auf die nötige Geschwindigkeit gebracht.
Mittlerweile sind Raumsonden mit immer komplizierteren [[Trajektorie (Physik)|Trajektorien]] gestartet worden: Die Jupitersonde [[Galileo (Raumsonde)|Galileo]] (1989) flog an der Venus und zweimal an der Erde vorbei, die Saturnsonde [[Cassini-Huygens]] (1997) zweimal an der Venus, an der Erde und am Jupiter. Die [[Rosetta (Sonde)|Rosetta-Mission]] (2004) erreichte über mehrere Swing-by-Manöver an Erde und Mars den Kometen [[Tschurjumow-Gerassimenko]], und die [[Parker Solar Probe]] (2018) nutzt sieben Vorbeiflüge an der Venus zum Abbremsen. Nach insgesamt neun Swing-bys an Erde, Venus und Merkur soll [[BepiColombo]] (2025) in eine Umlaufbahn um Merkur gelangen.<ref>https://sci.esa.int/web/bepicolombo/-/48871-getting-to-mercury</ref>
 
Selten werden Swing-bys dazu genutzt, die [[Bahnneigung|Inklination]] so stark zu ändern wie bei der Sonnensonde [[Ulysses (Sonde)|Ulysses]], um die Ebene der Ekliptik zu verlassen.
 
Die nicht verwirklichte [[Solar Probe +#Solar Probe|Solar Probe]] sollte durch einen Swing-by am [[Jupiter (Planet)|Jupiter]] auf eine polare Sonnenumlaufbahn gebracht werden, deren [[Perihel]] sich nur drei Sonnenradien über der Sonnenoberfläche befinden sollte und deren [[Aphel]] sich auf Höhe der Jupiterumlaufbahn befunden hätte.<ref>{{Internetquelle |hrsg=NASA |url=http://solarprobe.jhuapl.edu/mission/docs/SolarProbe_STDT2005.pdf |format=PDF mit 9,5&nbsp;MB |sprache=en |titel=Solar Probe: Report of the Science and Technology Definition Team |werk=NASA/TM-2005212-786 |seiten=ES-4, 4-1, 4-2 |datum=2005-09-00 |zugriff=2013-11-18 |archiv-url=http://web.archive.org/web/20160111003426/http://solarprobe.jhuapl.edu/mission/docs/SolarProbe_STDT2005.pdf |archiv-datum=2016-01-11}}</ref> Sie hätte damit nicht nur die Inklination wie [[Ulysses (Sonde)|Ulysses]] stark geändert, sondern wäre auch extrem abgebremst worden.
 
Auch für die [[Rosetta (Sonde)|Rosetta-Mission]] waren Swing-by-Manöver vorgesehen. Durch die Nichteinhaltung des ursprünglich berechneten Startzeitfensters zum Kometen [[46P/Wirtanen]] wegen Problemen mit der Rakete, musste eine neue Route gesucht werden, die dann über mehrere Swing-by-Manöver an Erde und Mars zu einer Annäherung an den Kometen [[Tschurjumow-Gerassimenko]] führte.
 
== Swing-bys in Animation ==
Die rote Kurve im jeweils unteren Bildteil zeigt die Geschwindigkeit der Raumsonde über die Zeit.
 
<gallery widths="240" heights="180">
Swingby acc anim.gif|Swing-by, um Geschwindigkeit aufzunehmen
Swingby dec anim.gif|Swing-by, um Geschwindigkeit abzubauen
</gallery>


== Siehe auch ==
== Siehe auch ==
* [[Fly-by-Anomalie]]
* [[Freie Rückkehrbahn]]
*[[Fly-by-Anomalie]]
* [[Gravitational keyhole]]
* [[Gravitational keyhole]]


== Literatur ==
== Literatur ==
* B. Stanek: ''Raumfahrtlexikon.'' Halwag Verlag, Bern (1983), ISBN 3-444-10288-7, S. 331–334.
* B. Stanek: ''Raumfahrtlexikon.'' Halwag Verlag, Bern (1983), ISBN 3-444-10288-7, S.&nbsp;331–334.
* Ernst Messerschmid, Stefanos Fasoulas: ''Raumfahrtsysteme: Eine Einführung mit Übungen und Lösungen.'' Springer Verlag, Berlin Heidelberg 2013, ISBN 978-3-662-09674-1, S.&nbsp;142–150 ({{Google Buch|BuchID=AEUhBgAAQBAJ|Seite=PA142}}).


== Weblinks ==
== Weblinks ==

Aktuelle Version vom 17. Februar 2022, 16:52 Uhr

Swing-by mit Ablenkung des Flug­körpers um 180° und 90°. Seine Geschwindig­keit relativ zum Planeten (blauer Pfeil) bleibt im Betrag gleich. Durch vektorielle Addition der Geschwindig­keit des Planeten relativ zur Sonne (gelber Pfeil) erhält man die Geschwindig­keit des Flug­körpers relativ zur Sonne (grauer Pfeil).

Der englische Begriff Swing-by – auch Slingshot, Gravity-Assist (GA), Schwerkraftumlenkung oder Vorbeischwungmanöver genannt – bezeichnet eine Methode der Raumfahrt, bei der ein relativ leichter Raumflugkörper (etwa eine Raumsonde) dicht an einem sehr viel größeren Körper (etwa einem Planeten) vorbeifliegt. Bei dieser Variante eines Vorbeiflugs wird die Flugrichtung der Sonde verändert, wobei auch deren Geschwindigkeit gesteigert oder gemindert werden kann. Ein Swing-by-Manöver kann auch mit einer Triebwerkszündung kombiniert werden. Bei sehr nahen Vorbeiflügen kann unter Umständen eine deutlich höhere Effizienz des Treibstoffs erreicht werden (Oberth-Effekt).

Der Swing-by-Effekt tritt auch auf, wenn ein Komet, ein Asteroid oder (wie es vermutlich in der frühen Geschichte des Sonnensystems geschah) ein leichterer Planet einen schwereren Planeten in dessen Gravitationsfeld passiert. Wenn die Masse des leichteren Planeten gegenüber dem schwereren nicht vernachlässigbar klein ist, ändert auch der schwerere Planet seine Sonnenumlaufbahn merklich.[1][2]

Prinzip

  • Zeitlicher Verlauf der Geschwindigkeit beim Swing-By

  • Swing-by, um Geschwindigkeit aufzunehmen

  • Swing-by, um Geschwindigkeit abzubauen

Bewegt sich eine Sonde durch das Gravitationsfeld eines Planeten, wird sie durch dessen Anziehungskraft abgelenkt. Bezogen auf den Planeten verändert sich der Betrag der Geschwindigkeit der Sonde in unendlicher Entfernung zum Planeten nicht, d. h. die Bahnenergie des Raumfahrzeugs bezogen auf den Planeten bleibt konstant. Nur die Richtung der Geschwindigkeit wird durch die Ablenkung verändert.

Hinzu kommt aber, dass sich der Planet um die Sonne bewegt. Die Geschwindigkeit der Sonde relativ zur Sonne ist die vektorielle Summe der Geschwindigkeit der Sonde relativ zum Planeten und der Geschwindigkeit des Planeten um die Sonne, und diese Summe ändert sich im Betrag. Bezogen auf die Sonne wird die Sonde somit schneller oder langsamer. Anders ausgedrückt: Die Gravitationskräfte zwischen Sonde und Planeten koppeln die beiden Bewegungen miteinander und ermöglichen einen Austausch von Bahnenergie zwischen beiden.

Auswirkungen

Grundsätzlich ergeben sich die folgenden Auswirkungen:

  • Änderung des Geschwindigkeitbetrages im übergeordneten Bezugssystem, d. h. der Bahnenergie des Raumfahrzeugs
  • Änderung der Flugrichtung innerhalb der Bahnebene des Bezugsystems (z. B. der Ekliptik) zum Anvisieren neuer Ziele
  • Änderung der Bahnebene, z. B. Verlassen der Ekliptik

Aufgrund der erheblich größeren Masse des Planeten verglichen mit dem Raumfahrzeug sind die Auswirkungen auf die Planetenbahn nicht messbar, während die Bahnenergie der Sonde sich erheblich verändern kann.

Swing-by-Manöver können damit auf interplanetaren Flügen zur Einsparung von Treibstoff dienen und daher auch Kosten reduzieren. Die Reisezeit kann durch die gewonnene Geschwindigkeit verkürzt werden, infolge von Umwegen aber auch steigen. Am Zielplaneten kann mit Swing-by an einem Trabanten (Mond) die Reisegeschwindigkeit abgebaut werden, um die Sonde in eine Umlaufbahn zu bringen.

Vergleich mit Stoßvorgängen

Vereinfachend kann zur Veranschaulichung der elastische Stoß zweier Körper herangezogen werden,[3] beispielsweise der frontale Kontakt eines Tischtennisballs mit einem Tischtennis­schläger. Wenn der Tischtennis­schläger unbeweglich ruht, prallt der Ball idealisiert (also ohne Berücksichtigung von Reibung) mit gleicher Geschwindigkeit wieder ab. Bewegt der Spieler den Schläger dem Ball entgegen, prallt dieser (aus Sicht des Zuschauers) mit höherer Geschwindigkeit zurück; umgekehrt kann der Spieler durch „Zurücknehmen“ des Schlägers den Ball abbremsen. Aus „Sicht“ (Inertialsystem) des Schlägers prallt er stets mit gleicher Geschwindigkeit zurück, sonst wäre es kein elastischer Stoß.

Trajektorie von Voyager 2
  • Voyager 2
  • Sonne
  • Erde
  • Jupiter
    		•
  • Saturn
  • Uranus
  • Neptun

    • Wenn sich Ball und Schläger nicht frontal treffen, muss noch die seitliche Geschwindigkeits­komponente berücksichtigt werden; ebenso ist es beim Swing-by, da die Raumsonde nicht frontal auf den Planeten trifft. Beim Swing-by findet die Wechselwirkung über einen längeren Zeitraum statt, aber das Grundprinzip ist gleich.

    Routenplanung

    Da es sich in der Realität mindestens um ein Dreikörperproblem handelt (z. B. Sonde, Planet und Sonne), sind die Bahnänderungen nicht analytisch, sondern nur numerisch genauer zu berechnen. Da der Flugwinkel und die Geschwindigkeit nach der Passage voneinander abhängen, ist der Spielraum für die Entfernung und die Position des nächsten Zielobjektes begrenzt. Bei Vorgabe mehrerer Ziele und/oder Einschränkung auf eine bestimmte Anflugbahn und Geschwindigkeit beim Ziel entsteht ein Gleichungssystem, das numerisch auf Lösungen überprüft wird. Die Lösungen (Trajektorien) ergeben zumeist nur schmale Startzeitfenster in der Größenordnung von Tagen oder Wochen, die für die gleichen Missionsziele Jahre oder viele Jahrzehnte auseinander liegen können. Die Startgeschwindigkeit von der Erde und damit die Kosten der Raketen, sowie die Dauer der Mission sind ebenfalls Vorgaben oder Ergebnisse der Berechnungen.

    Der Tisserandparameter wird bei der Planung von Gravity-Assists verwendet, um mögliche Partnerkörper zu finden. Es handelt sich um eine näherungsweise Erhaltungsgröße, welche sich aus verschiedenen geometrischen Bahnparametern ergibt und vor und nach einem Gravity-Assist ungefähr gleich ist. Somit ergibt sich eine Einschränkung, welche Bahn überhaupt möglich ist.[4]

    Geschichte

    Geschwindigkeits­profil der Sonde Voyager 2. Erst durch Swing-by am Jupiter konnte die Flucht­geschwindig­keit aus dem Sonnen­system (solar escape velocity) erreicht werden. Weiterer Geschwin­digkeits­zuwachs erfolgte an Saturn und Uranus. Am Neptun wurde die Sonde nahe an dessen Mond Triton geführt; dabei wurde Geschwin­digkeits­verlust in Kauf genommen.

    Swing-by-Manöver zur Änderung der Flugrichtung fanden schon in der Frühzeit der Raumfahrt statt, so bei der Sonde Luna 3 (1959), die als erste den Mond umrundete und wieder Kurs auf die Erde nahm.[5] Auch bei Apollo 13 (1970) wurde ein Swing-by-Manöver verwendet, um den Mond in einer Schleife zu umfliegen und direkt zurückzukehren.[6] Bei der Sonnensonde Ulysses (1990) wurde ein Swing-by am Jupiter dazu genutzt, die Inklination zu ändern, um die Ebene der Ekliptik zu verlassen.

    Dass man Raumsonden durch Swing-by zusätzliche Geschwindigkeit verleihen kann, entdeckte 1961 Michael Minovitch, der am Jet Propulsion Laboratory arbeitete.[7][8] Zuvor hatte es als ausgeschlossen gegolten, dass man jemals mit konventioneller Raketentechnik die Planeten des äußeren Sonnensystems erreichen könnte. Der Grund dafür ist das theoretisch angenommene energetische Minimum, das durch einen Hohmann-Transfer gegeben ist,[8][9] und die Tatsache, dass nach der Raketengrundgleichung die erforderliche Startmasse des Raumfahrzeugs exponentiell mit der benötigten Endgeschwindigkeit wächst.

    Die ersten interplanetaren Sonden, die diese Technik nutzten, waren Pioneer 10 (1972: Erde → Jupiter → interstellarer Raum), Pioneer 11 (1973: Erde → Jupiter → Saturn → interstellarer Raum) und Mariner 10 (1973: Erde → Venus → Merkur)[10]. Von besonderer Bedeutung wurde Swing-by für die beiden Voyager-Sonden (1977): Aufgrund einer Planetenkonstellation, wie sie nur alle 176 Jahre vorkommt, konnte Voyager 2 nacheinander die Planeten Jupiter, Saturn, Uranus und Neptun besuchen und dabei, ebenso wie ihre Schwestersonde Voyager 1, die Jupiter und Saturn besuchte, die dritte kosmische Geschwindigkeit erreichen, die sie in den interstellaren Raum brachte.

    Flugbahn der NASA/ESA-Raumsonde Cassini-Huygens: Nach dem Start von der Erde flog sie zweimal an der Venus, einmal an der Erde und einmal am Jupiter vorbei, bis sie durch diese Swing-by-Manöver genug kinetische Energie hatte, ihr Ziel, den Saturn, erreichen zu können.

    Mittlerweile sind Raumsonden mit immer komplizierteren Trajektorien gestartet worden: Die Jupitersonde Galileo (1989) flog an der Venus und zweimal an der Erde vorbei, die Saturnsonde Cassini-Huygens (1997) zweimal an der Venus, an der Erde und am Jupiter. Die Rosetta-Mission (2004) erreichte über mehrere Swing-by-Manöver an Erde und Mars den Kometen Tschurjumow-Gerassimenko, und die Parker Solar Probe (2018) nutzt sieben Vorbeiflüge an der Venus zum Abbremsen. Nach insgesamt neun Swing-bys an Erde, Venus und Merkur soll BepiColombo (2025) in eine Umlaufbahn um Merkur gelangen.[11]

    Siehe auch

    Literatur

    • B. Stanek: Raumfahrtlexikon. Halwag Verlag, Bern (1983), ISBN 3-444-10288-7, S. 331–334.
    • Ernst Messerschmid, Stefanos Fasoulas: Raumfahrtsysteme: Eine Einführung mit Übungen und Lösungen. Springer Verlag, Berlin Heidelberg 2013, ISBN 978-3-662-09674-1, S. 142–150 (eingeschränkte Vorschau in der Google-Buchsuche).

    Weblinks

    Commons: Gravitational slingshots – Sammlung von Bildern, Videos und Audiodateien
    • Michael Müller: Swing-by. Im Archiv von: Erkenntnishorizont.de.

    Einzelnachweise

    1. ↑ Stefan Deiters: Sonnensystem. Gab es einst fünf Gasriesen? astronews.com, 16. November 2011, abgerufen am 16. April 2014.
    2. ↑ Laura Hennemann: Sonnensystem. Der verstoßene Planet. sterne-und-weltraum.de, 15. November 2011, abgerufen am 16. April 2014. (Der Artikel nennt als Quelle: arxiv:1109.2949)
    3. ↑ A Gravity Assist Primer. JPL/NASA, archiviert vom Original am 26. Juli 2016; abgerufen am 16. April 2014 (Lua-Fehler in Modul:Multilingual, Zeile 149: attempt to index field 'data' (a nil value)).
    4. ↑ James Miller & Connie Weeks: Application of Tisserand's Criterion to the Design of Gravity Assist Trajectories. (PDF) In: AIAA/AAAS Astrodynamics Specialist Conference. AIAA, 2002, abgerufen am 15. Dezember 2022 (Lua-Fehler in Modul:Multilingual, Zeile 149: attempt to index field 'data' (a nil value)).
    5. ↑ Luna 3 orbit. The Planetary Society, abgerufen am 17. Dezember 2018.
    6. ↑ W. David Woods: How Apollo Flew to the Moon. Springer (eingeschränkte Vorschau in der Google-Buchsuche).
    7. ↑ M. Minovitch: Gravity Assist.
    8. ↑ 8,0 8,1 Richard L. Dowling et al: The Effect of Gravity-Propelled Interplanetary Space Travel on the Exploration of the Solar System: Historical Survey, 1961 to 2000. (PDF) In: History of Rocketry and Astronautics, AAS History Series, Vol 28. Donald C Elder, S. 339, abgerufen am 17. Dezember 2018 (Lua-Fehler in Modul:Multilingual, Zeile 149: attempt to index field 'data' (a nil value)).
    9. ↑ Reiner Klingholz: Marathon im All: die einzigartige Reise der Voyager 2. Ullstein, 1992, ISBN 3-548-34870-X, S. 23.
    10. ↑ SP-424 Mariner Venus-Mercury Mission. Bei: History.NASA.gov.
    11. ↑ https://sci.esa.int/web/bepicolombo/-/48871-getting-to-mercury
    Abgerufen von „https://www.cosmos-indirekt.de/physik_137/index.php?title=Swing-by&oldid=14526“