Gezeitenkraft
Gezeitenkräfte treten auf, wenn sich ein ausgedehnter Körper in einem äußeren Gravitationsfeld befindet, dessen Stärke räumlich variiert. Die auf der Erde nachweisbaren Gezeitenkräfte werden durch Mond und Sonne verursacht und rufen (unter anderem) die Gezeiten der Meere hervor.
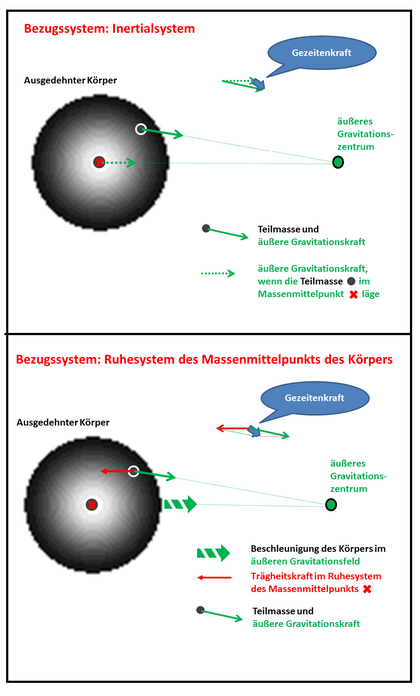
Die Gezeitenkraft auf einen bestimmten Teil des ausgedehnten Körpers ist die Differenz der äußeren Gravitationskraft, die auf diesen Teil an seinem Ort wirkt, und der Gravitationskraft, die auf ihn wirken würde, wenn er sich am Ort des Massenmittelpunktes des ausgedehnten Körpers befände (siehe Abbildung, oberer Teil). Drei dazu äquivalente Definitionen sind: (1) Die Gezeitenkraft auf einen Teil des Körpers ist die Summe aus der äußeren Gravitationskraft und der Trägheitskraft, die sich aus der Beschleunigung des Massenmittelpunkts des ausgedehnten Körpers ergibt (siehe Abbildung, unterer Teil). (2) Die Gezeitenkraft ist die äußere Gravitationskraft, wie sie sich in dem beschleunigten Bezugssystem auswirkt, in dem der Massenmittelpunkt des ausgedehnten Körpers ruht. (3) Die Gezeitenkräfte ergeben sich aus den Gezeitenbeschleunigungen, das sind die Unterschiede in der Fallbeschleunigung, die verschiedene Teile des ausgedehnten Körpers in dem äußeren Gravitationsfeld erfahren.
Gezeitenbeschleunigungen sind relativ klein im Vergleich zu der Beschleunigung, die der ausgedehnte Körper als Ganzes durch das äußere Gravitationsfeld erfährt. Bemerkbar werden Gezeitenkräfte vor allem dann, wenn das System keinen weiteren äußeren Kräften unterworfen ist, sich also z. B. in einer Umlaufbahn frei bewegt oder, allgemein gesagt, sich im freien Fall befindet.
In der Allgemeinen Relativitätstheorie wird das durch den Riemannschen Krümmungstensor der Raum-Zeit beschriebene Verhalten benachbarter Geodäten, die aufgrund der Raumzeitkrümmung aufeinander zulaufen oder sich voneinander entfernen, ebenfalls als Gezeitenkraft bezeichnet.
Wirkung von Gezeitenkräften
Die Gezeitenkräfte bewirken eine Verformung ausgedehnter Körper oder Systeme. Beispiele für die Wirkung von Gezeitenkräften sind, neben den Gezeiten, die Abbremsung der Erdrotation, die gebundene Rotation des Erdmondes, der Vulkanismus des Jupitermondes Io und das Auseinanderreißen von Kometen (siehe z. B. Shoemaker-Levy 9) oder Galaxien bei Beinahezusammenstößen (siehe z. B. Antennen-Galaxien).
Ein typisches inhomogenes Gravitationsfeld ist das Zentralfeld, das durch einen entfernten Körper erzeugt wird. Ein ausgedehnter Körper, der darin frei fällt, wird parallel zur Richtung des Fallens (im Bild waagerecht) gestreckt, senkrecht dazu gestaucht. Ein einfacher Probekörper zur Erkundung der Gezeitenbeschleunigung ist eine Hantel in Gestalt zweier starr verbundener Punktmassen. Die Hantel gerät unter eine Zugspannung (ihre Massen streben auseinander), wenn sie radial, also parallel zur Fallbeschleunigung orientiert ist. Dagegen gerät sie unter eine Druckspannung von der halben Größe dieser Zugspannung, wenn sie quer zur Fallrichtung orientiert ist. Liegt sie schräg zu einer dieser Richtungen, erfährt sie ein Drehmoment, das sie in die radiale Orientierung dreht. Dies gilt entsprechend auch für näherungsweise kugelförmige Körper, wenn sie gestreckt oder gestaucht sind. Für eine Anwendung siehe Stabilisierung (Raumfahrt).
Ein kugelsymmetrischer Körper erfährt insgesamt kein Drehmoment. Die Gezeitenkräfte an seiner Oberfläche sind an den beiden Punkten des kleinsten bzw. größten Abstands zum Mittelpunkt des Zentralfelds radial nach außen gerichtet. In gewissem Abstand von diesen beiden Punkten sind die Gezeitenkräfte parallel zur Oberfläche und auf diese Punkte hin gerichtet. Auf der Erde, die im Gezeitenpotential von Mond und Sonne rotiert, erzeugen sie in den Wassermassen der Ozeane periodisch Strömungen, die an den Küsten Ebbe und Flut verursachen, eben die Gezeiten.
In der Geophysik und Planetologie gibt die Messung von Verformungen durch Gezeitenkräfte auch Hinweise auf die Elastizität und den inneren Aufbau von Planeten. In den 1980er Jahren wurden mathematisch-physikalische Erdmodelle entwickelt, die den Unterschied zwischen starrer und elastischer Erde mittels Shida- und Love-Zahlen beschreiben. Neben den Ozeanen hebt sich auch die feste Erdkruste 2 × täglich um ±(30 bis 50) cm. Heute ist diese Theorie auf einige mm genau und dient zur Reduktion aller geodätischen Erdbeobachtungen und sogar von Satellitenbahnen.
Maximale Werte der Gezeitenbeschleunigung an einem Trabanten
Ein Zentralkörper der Masse M verursacht auf der Oberfläche eines Trabanten, der den Radius R hat und sich mit seinem Mittelpunkt im Abstand r befindet, im nächsten und fernsten Punkt die Gravitationskraft:
- (1) $ a_{g}\approx \mp \ 2R\ {\frac {GM}{r^{3}}} $
Das Vorzeichen ist hier auf den Mittelpunkt des Zentralkörpers bezogen. Vom Mittelpunkt des Trabanten aus gesehen weist die Gezeitenbeschleunigung hingegen an beiden Punkten nach außen.
Herleitung
Die mittlere Gravitationsbeschleunigung $ a_{m} $, die auf den ganzen Trabanten wirkt, ist
- (2) $ a_{m}={\frac {GM}{r^{2}}}{\text{ }} $.
Der dem Zentralkörper nächste Punkt an der Oberfläche des Trabanten hat den Abstand $ r-R $, der fernste $ r+R{\text{ }} $. Die Gravitationsbeschleunigung $ a_{r} $ an diesen Punkten ist daher
- (3) $ a_{r}={\frac {GM}{(r\pm R)^{2}}}{\text{ }}. $
Dies ist die größte bzw. kleinste Gravitationsbeschleunigung, die auf ein Massenelement des Trabanten wirkt. Sie ist im „vorderen“ Punkt also größer und im „hinteren“ kleiner als $ a_{m} $.
Die Gezeitenbeschleunigung an jedem Punkt ist ganz allgemein die vektorielle Differenz zwischen der dort herrschenden Gravitationsbeschleunigung und der mittleren Gravitationsbeschleunigung des Körpers. Da alle drei Beschleunigungen im vorliegenden Fall parallel sind, folgt:
- (4) $ a_{g}={\frac {GM}{(r\pm R)^{2}\ }}-{\frac {GM}{r^{2}}}={\frac {GM}{r^{2}}}\left({\frac {1}{(1\pm R/r)^{2}}}-1\right) $
Wenn $ R\ll r $ gilt, wie in den meisten Fällen, kann man den Bruch durch
- (5) $ {\frac {1}{(1\pm R/r)^{2}}}=1\mp \ 2R/r+3(R/r)^{2}\mp \dots $
wiedergeben und die unendliche Reihe näherungsweise nach dem linearen Glied abbrechen. Es folgt:
- (6) $ a_{g}\approx \ {\frac {GM}{r^{2}}}((1\mp \ 2R/r)-1)=\mp \ 2R{\frac {GM}{r^{3}}} $
Die Gezeitenbeschleunigung weist auf beiden Seiten vom Mittelpunkt des Trabanten weg. Sie ist genau genommen nicht auf beiden Seiten gleich groß, wie man sieht, wenn man die Näherung bis zum quadratischen Glied oder gleich die ungenäherte Formel nimmt.
Eine Gezeitenbeschleunigung zum Mittelpunkt des Trabanten ergibt sich für die Punkte der Oberfläche, die vom Zentralkörper den gleichen Abstand haben. Dort sind zwar die Beträge der Gravitationsbeschleunigung zum Zentralkörper gleich groß wie die mittlere Beschleunigung, aber nicht ihre Richtungen. Verglichen mit der am Mittelpunkt angreifenden Beschleunigung $ a_{m} $ haben sie eine nach innen gerichtete Komponente der Größe $ a_{m}{\tfrac {R}{r}} $, also der Hälfte des Wertes für die Punkte mit minimalem oder maximalem Abstand zum Zentralkörper.
Roche-Grenze
Ist der Abstand eines Trabanten zu seinem Zentralkörper sehr klein, so werden die Gezeitenkräfte sehr stark.
Um die Stabilität eines Körpers zu untersuchen, betrachtet man die Gezeitenkräfte im Vergleich zu den Gravitationskräften, die den Körper selbst zusammenhalten. Im Stabilitätsbereich sind die Gezeitenkräfte nicht größer als die Gravitationskräfte, wobei man zur Abschätzung den Trabanten in zwei Teilkörper unterteilt, mit jeweils der halben Trabantenmasse $ M_{t}/2 $ in einem Abstand, der seinem Radius $ R_{t} $ entspricht:
- $ G{\frac {M_{t}^{2}}{4R_{t}^{2}}}\geq cG{\frac {MM_{t}}{r^{3}}}\cdot R_{t} $
mit dem Abstand r von der Zentralmasse $ M $, c ist hierbei eine Konstante von der Größenordnung 1. Mit den mittleren Dichten ρ und ρt des Zentralkörpers und des Trabanten sowie dem Radius R des Zentralkörpers erhält man:
- $ {\frac {r}{R}}\geq (4c)^{1/3}\left({\frac {\rho }{\rho _{t}}}\right)^{1/3} $
Eine genauere Rechnung ergibt:
- $ {\frac {r}{R}}\geq 2{,}44\left({\frac {\rho }{\rho _{t}}}\right)^{1/3} $
Bei einem Abstand von weniger als dem 2,44-Fachen des Radius seines Zentralkörpers wird ein Trabant mit gleicher Dichte durch die Gezeitenkräfte auseinandergerissen bzw. kann sich gar nicht erst bilden. Dieser Abstand wird nach Édouard Albert Roche, der diese Abschätzung erstmals durchgeführt hat, „Roche-Grenze“ genannt.
Diese Überlegungen gelten für die eigene Schwerkraft als relevanten Gegenspieler der Gezeitenkraft, der für Zusammenhalt sorgt, also für den Fall größerer Körper (vgl. Zwergplanet). Bei kleineren Körpern überwiegt jedoch die Stabilisierung durch Kohäsionskräfte.
Bei künstlichen Satelliten ist die eigene Gravitation für die Betrachtung des Zusammenhalts vernachlässigbar gegenüber der Zug- und Druckfestigkeit und Steifigkeit der Konstruktionsmaterialien. Wo keine mechanisch feste Verbindung besteht, können Gezeitenkräfte spürbar werden: Beim Schweben eines Astronauten außerhalb oder auch innerhalb der Kapsel, beim Entschweben von Werkzeug ohne Fangleine, bei einem Koppelmanöver von zwei Raumfahrzeugen, bei Flüssigkeit in einem halbvollen Tank.
Kosmische Beispiele
Roche-Grenze unterschritten
Die Saturnringe liegen zum großen Teil innerhalb der Roche-Grenze des Saturns. Dies ist neben den Hirtenmonden, deren Stabilität durch innere Kohäsionskräfte erhöht wird, der Hauptgrund für die Stabilität des Ringsystems.
Der Komet Shoemaker-Levy 9 passierte im Juli 1992 den Planeten Jupiter und zerbrach dabei in 21 Fragmente zwischen 50 und 1000 m Größe, die sich auf einer mehrere Millionen Kilometer langen Kette aufreihten. Zwischen dem 16. und dem 22. Juli 1994 tauchten diese Bruchstücke dann in Jupiter ein.
Bei engen Begegnungen von Sternen mit einem Abstand, der geringer ist als die Roche-Grenze, werden diese in einer sogenannten Sternkollision stark verändert, meist wird der kleinere zerrissen.
Roche-Grenze nicht unterschritten
Die Gezeitenwirkung des Jupiters verhindert, dass sich der Asteroidengürtel zu einem Planeten zusammenballt. Wenn zum Beispiel zwei Asteroiden Jupiter passieren, zieht dieser den ihm näher gelegenen stärker an als den entfernteren. Die Distanz zwischen den Asteroiden vergrößert sich.
Auf der Erde führen die Gezeiten in den Meeren zu Ebbe und Flut. Die Gezeiten wirken jedoch auch auf den Erdmantel selbst, sodass auch die Kontinente den Gezeiten mit einer Verzögerung von zwei Stunden folgen, allerdings ist der Effekt mit Vertikalbewegungen von 20 bis 30 Zentimeter deutlich geringer als die mehrere Meter hohen Tiden der Meere.
Durch die Gezeiten in großen Meeren können durch den Tidenhub lokal sehr starke Strömungen entstehen. Die dabei vorhandene kinetische Energie kann mittels eines Gezeitenkraftwerks genutzt werden.
Gezeitenreibung (Roche-Grenze nicht unterschritten)
Die Gravitationskräfte, die einander umkreisende Körper aufeinander ausüben, bewirken eine meist schwache Kopplung von Rotation und Revolution. Dadurch wird meist Rotationsdrehimpuls in Bahndrehimpuls verwandelt – selten umgekehrt, weil Rotationen typischerweise größere Winkelgeschwindigkeiten besitzen als die Bahnbewegung. Folgende Darstellung des Mechanismus, also der Ursache des Drehmomentes zwischen Rotation und Revolution, spricht dabei von einem rotierenden und einem „fernen“, vereinfacht gesagt dem „anderen“, meist größeren Körper (z. B. dem betreffenden Zentralgestirn), wobei, falls beide rotieren, der Effekt auch mit vertauschten Rollen auftreten kann.
Unter der Gezeitenbeschleunigung des fernen Körpers nimmt der rotierende Körper eine leicht längliche (prolate) Form an. Aufgrund innerer Reibung bei der Verformung ist die Längsachse nicht auf den fernen Körper ausgerichtet, sondern in Rotationsrichtung verdreht. Die Wechselwirkung des fernen Körpers mit dem ihm zugewandten Ende des rotierenden Körpers ist stärker als mit dem abgewandten Ende. Der effektive Angriffspunkt für die Gesamtkraft, das sogenannte Gravizentrum, liegt nicht mehr auf der Verbindungslinie der Baryzentren der beiden Körper, sondern ist etwas in Rotationsrichtung verschoben, was das Drehmoment erklärt.
Das Zeitintegral des Drehmoments ist der Drehimpuls, den der rotierende Körper verliert. Drehimpuls ist eine vektorielle Erhaltungsgröße. Was der rotierende Körper an Drehimpuls verliert, addiert sich vektoriell zum Bahndrehimpuls des Systems. Dadurch nimmt der Bahndrehimpuls betragsmäßig zu, falls die Richtungen passen (oder ab, falls der ferne Körper schneller umläuft als der Zentralkörper sich dreht, Beispiel Phobos, oder gegen die Rotationsrichtung umläuft, Beispiel Triton). Höherer Bahndrehimpuls bewirkt nicht etwa eine höhere, sondern eine geringere Bahngeschwindigkeit – auf einer größeren Bahn, siehe das dritte Keplersche Gesetz.
Auf lange Sicht kann die Rotation in eine gebundene Rotation übergehen. Dieses Schicksal trifft meist den kleineren Körper zuerst, wie beim Erdmond. Solange die Rotation noch viel schneller ist als die Revolution, wird der größte Teil der Rotationsenergie, die der rotierende Körper verliert, nicht als Arbeit am fernen Körper geleistet, sondern geht überwiegend als Wärme verloren. Im Fall des retrograd umlaufenden Triton wird auch Bahnenergie und gravitative Bindungsenergie als Wärme frei – der Mond driftet nach innen, zur Roche-Grenze seines Planeten Neptun, wo er in weniger als einer Milliarde Jahre in ein Ringsystem zerrissen wird.
Beispiel Erde-Mond-System
Zum Drehmoment zwischen Erde und Mond tragen hauptsächlich die Gezeiten bei. Die Verformung des Erdmantels ist auf der kurzen Zeitskala der Erdrotation weit überwiegend elastisch und daher wenig phasenverschoben gegenüber der Gezeitenbeschleunigung. Die Atmosphäre dagegen hat zu wenig Masse, um viel beizutragen. Für Zahlenangaben zu aktuellen Änderungsraten siehe Langfristige Änderungen der Erdrotation und Säkulare Akzeleration der Mondbahn.
Zusammenfassung der Auswirkungen
- Durch Gezeitenkräfte verformen sich Himmelskörper, sie werden geringfügig auf der Linie durch ihren Schwerpunkt und den des anderen Körpers in die Länge gezogen. Rotiert der Himmelskörper, so wird er dabei „durchgewalkt“, ähnlich wie ein platter Reifen am Auto. Dadurch wird Rotationsenergie in Wärme umgewandelt; die Rotation verlangsamt sich dadurch so lange, bis sich eine gebundene Rotation einstellt. Der Erdmond weist der Erde aufgrund dieses Effektes immer die gleiche Seite zu, und der Erdkern wird erhitzt. Beim Jupitermond Io sind es Gezeitenkräfte, die die Wärmeenergie für den Vulkanismus bereitstellen.
- Die Verformung des Erdkörpers ist gering, dagegen ist die Auswirkung auf das beweglichere Wasser an seiner Oberfläche deutlich. Es entstehen die maritimen Gezeiten, woher der Name Gezeitenkraft stammt.
- In Doppelsternsystemen können Gezeitenkräfte einen Materiefluss von einem Stern zum anderen verursachen, was in bestimmten Fällen zu einer Supernova (Typ 1a) führen kann.
- Sind die Gezeitenkräfte stärker als die Kräfte, die ein Objekt zusammenhalten, so können sie auch zum Zerreißen des Objekts führen, so geschehen beim Kometen Shoemaker-Levy 9 (siehe Roche-Grenze).
Siehe auch
- Spaghettisierung (extreme Verformung eines Objekts, das in die Nähe eines Schwarzen Lochs gerät)
Literatur
- David E. Cartwright: Tides – a scientific history. Cambridge Univ. Press, Cambridge 1999, ISBN 0-521-62145-3 (englisch).
- Rainer Müller: Klassische Mechanik. 3. Auflage. de Gruyter, Berlin 2015, Kap. 12.
- Georg Hamel: Theoretische Mechanik. Berichtigter Reprint. Springer, Berlin / Heidelberg / New York 1978. ISBN 3-540-03816-7. Kap. VIII, S. 379.
- Friedhelm Kuypers: Klassische Mechanik. 9. Auflage. WILEY-VCH, Weinheim 2010, ISBN 978-3-527-40989-1, S. 182 f., 553–557.
Weblinks
- Die Gezeiten. (Memento vom 17. April 2008 im Internet Archive).
- N. Gasch: Rhythmen des Mondes – Geologische Zeugnisse aus alter Zeit.
- Gezeiten-Simulation auf beltoforion.de (Javascript)
- Gezeiten-Simulation auf wissen.swr.de (Flash Player)
