Radialgeschwindigkeit
Bei vektorieller Darstellung einer beliebigen Bewegung in Polar- oder Kugelkoordinaten bezeichnet die Radialgeschwindigkeit (von lat. radius »Stab«, »Radspeiche«) die Geschwindigkeitskomponente entlang des Strahls (Radius), der vom Koordinatenursprung zum betrachteten Objekt zeigt.
Die anderen Geschwindigkeitskomponenten sind dabei zeitlich veränderliche Winkel, also Rotationen, während es sich bei der Radialgeschwindigkeit um eine Translation handelt.
Bei Beobachtungen kann die Radialgeschwindigkeit direkt aus der Frequenzverschiebung des zur Beobachtung verwendeten Trägersignals geschlossen werden (Dopplereffekt). Dabei beobachtet man entweder die Veränderung einer vom Objekt reflektierten Welle (Sonar, Radar) oder die Veränderung einer vom Objekt ausgesendeten Welle (beobachtende Astronomie), sofern deren Ursprungsfrequenz bekannt ist. Als Besonderheit tritt die Dopplerfrequenz bei einer reflektierten Welle auf dem Hin- und auf dem Rückweg auf, hat also den doppelten Wert wie bei einer vom Objekt ausgesendeten Welle.
Radar- und Sonartechnik
In der Radar- und Sonartechnik ist die Radialgeschwindigkeit das Maß für eine dem Sendesignal auferlegte Dopplerfrequenz. Die Auswertung der Dopplerfrequenz wird zur Unterscheidung von bewegten und unbewegten Objekten verwendet (Moving Target Indication): die Eigenschaft „bewegt“ kann nur erkannt werden, wenn eine Radialgeschwindigkeit vorliegt; bewegt sich ein Objekt nur mit einer Tangentialgeschwindigkeit, so wird es nur als unbewegtes Objekt erkannt.
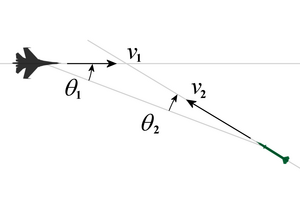
Wenn ein Radar von einer bewegten Plattform aus betrieben wird, so fließen beide Geschwindigkeiten in die Radialgeschwindigkeit ein, es müssen beide Bewegungsrichtungen durch eine Cosinus-Beziehung berücksichtigt werden. Als Radialgeschwindigkeit wird bei in etwa entgegengesetzter Bewegungsrichtung gemessen:
- $ v_{r}=v_{1}\cdot \cos {\theta _{1}}+v_{2}\cdot \cos {\theta _{2}} $
wobei v1 und v2 die jeweiligen Geschwindigkeiten von Radar und reflektierendem Objekt, die Winkel θ1 und θ2 die Winkelabweichungen der Kurse von der direkten Sichtlinie zueinander sind. Haben Plattform und reflektierendes Objekt annähernd gleiche Bewegungsrichtung, so ändert sich in der Gleichung mindestens ein Vorzeichen, da einer der Winkel größer als 90° wird und dessen Cosinus deshalb negativ wird.
Astronomie
Analog zu der allgemeinen Definition ist in der Astronomie die Radialgeschwindigkeit die Geschwindigkeitskomponente eines Himmelskörpers in Richtung der Sichtlinie eines Beobachters. Das Licht eines Objekts mit erheblicher Radialgeschwindigkeit unterliegt dem Dopplereffekt:
| Objekt … | … entfernt sich | … nähert sich |
|---|---|---|
| Radialgeschwindigkeit | $ v_{r}>0 $ | $ v_{r}<0 $ |
| Wellenlänge $ \lambda $ des Lichts … |
… wird vergrößert | … wird verkleinert |
| Verschiebung der Spektrallinien |
Rotverschiebung $ (z>0) $ |
Blauverschiebung $ (z<0) $ |
| Frequenz des Lichts … |
… sinkt | … steigt |
Die Radialgeschwindigkeit eines Sterns oder eines anderen leuchtenden, entfernten Objekts kann präzise gemessen werden, indem ein hochaufgelöstes Spektrum von ihm aufgenommen wird und dessen Spektrallinien mit den aus Laborversuchen bekannten Spektrallinien verglichen werden. Die daraus ermittelte Rot- bzw. Blauverschiebung lässt sich direkt in eine Geschwindigkeit umrechnen. Auf diesem Weg ist es allerdings nur möglich, die Geschwindigkeitskomponente in Richtung zur Sonne zu ermitteln, nicht die Komponente senkrecht zur Sichtlinie (Tangentialgeschwindigkeit).
Räumliche Dynamik von Sternsystemen und Galaxien
Die Messung von Radialgeschwindigkeiten (abgekürzt RG) ist u. a. ein wesentlicher Beitrag zur Erforschung der Dynamik von Sternhaufen, in größerem Maßstab auch von Galaxien und für die Kosmologie. Wenn von Himmelskörpern die räumliche Position (Koordinaten α, δ plus Entfernung) sowie die zwei Komponenten der Eigenbewegung bekannt sind, gibt die RG den vollständigen Geschwindigkeitsvektor.
Damit lassen sich im Rahmen der Himmelsmechanik verschiedene Bewegungsmodelle erstellen, beispielsweise für Doppel- und Mehrfachsterne, für Sternhaufen und Sternströme, für die Rotation der Milchstraße, die Verteilung der Dunklen Materie oder die Gezeitenkräfte zwischen Galaxien.
Einige Beispiele für Radialgeschwindigkeiten:
- Naher Stern Arktur (α im Sternbild Bootes): −5 km/s.
- Wildentenhaufen M 11, ein offener Sternhaufen: +22 km/s.
- Andromedagalaxie M 31: −301 km/s, sie bewegt sich also auf uns zu.
- Galaxie Messier 66 (30 Millionen Lichtjahre): +727 km/s.
Die 3 erstgenannten Radialgeschwindigkeiten sind heliozentrisch, wie sie sich aus spektroskopischen Messungen der Blau- bzw. Rotverschiebung von Spektrallinien des jeweiligen Objekts im Jahresverlauf ergeben (dazu ist eine geeignete Mittelbildung erforderlich). Für die Nachbargalaxie M 31 und fernere Galaxien sind aber weitere Reduktionen vorzunehmen:
Da nämlich die Sonne (und damit die erdgebundene Beobachtung) mit hoher Geschwindigkeit um das galaktische Zentrum kreist, entspricht die heliozentrische Radialgeschwindigkeit nicht der Geschwindigkeit, mit der sich M31 und die Milchstraße aufeinander zubewegen; dieser Wert liegt mit −114 km/s deutlich niedriger.
Spektroskopische Doppelsterne und Exoplaneten
Bei Doppelsternsystemen bewirkt die Umlaufbewegung der beteiligten Sterne eine fortwährende Veränderung ihrer Radialgeschwindigkeiten. Dadurch ist auch bei teleskopisch nicht trennbaren Sternen feststellbar, dass es sich um Zwei- oder Mehrfachsysteme handelt (→ spektroskopische Doppelsterne). Durch genaue Analyse der Radialgeschwindigkeiten können die Massenverhältnisse und einige Bahnelemente, wie Exzentrizität und große Halbachse abgeschätzt werden.
Die gleiche Methode wurde sehr erfolgreich verwendet, um ansonsten unsichtbare Planeten (Exoplaneten) um Sterne nachzuweisen.[1] Auch die Rotationsgeschwindigkeiten größerer astronomischer Objekte, wie Galaxien und Galaxienhaufen, lassen sich mit Hilfe der unterschiedlichen Radialgeschwindigkeiten des enthaltenen Materials bestimmen.
Einzelnachweise
- ↑ Chris Kitchin: Exoplanets, Finding, Exploring and Understanding Alien Worlds, Springer 2012, Seite 71 ff.
Siehe auch
- Hubble-Effekt
- Eigenbewegung