Entfernungsmessung

Unter Entfernungsmessung, Abstandsmessung oder Längenmessung versteht man die Messung des Abstandes zweier Punkte im Raum durch direkten oder indirekten Vergleich mit einer Längenmaßeinheit wie beispielsweise dem Meter. Der Bereich möglicher Längen beginnt bei der sogenannten Planck-Länge von rund $ 10^{-35} $ Meter. Das ist die kleinste Länge, in die sich der Raum einteilen lässt. Der physikalisch relevante Bereich beginnt bei $ 10^{-18} $ Metern, der Größe der Elementarteilchen, und reicht bis $ 10^{26} $ Meter. Er überspannt damit $ 44 $ Größenordnungen – von der Atomphysik über die Biologie und Technik bis zu den fernsten Galaxien. Daraus ergibt sich, dass eine sehr große Zahl unterschiedlicher Verfahren notwendig ist, um Entfernungen zu messen.

Kombiniert man Entfernungs- und Richtungsmessung, kann die Lage von Punkten in einem ebenen oder räumlichen Koordinatensystem festgelegt werden – siehe Geometrie, Vermessung, Ortung, Navigation und Astrometrie.

Das folgende Schaubild gibt einen Überblick über die Einheitenvorsätze bei Längen- und Entfernungsmessungen, enthält Beispiele für die Größenbereiche und ordnet die jeweiligen Messprinzipien zu.

Messprinzipien

Entfernungsmessen beim Militär (1903)

Direkte Messung

Die unmittelbarste Form der Entfernungsmessung ist die sogenannte direkte Messung. Darunter versteht man den direkten Vergleich der zu bestimmenden Entfernung mit einem Maßstab. Diese Art der Messung ist nur in einem begrenzten Längenbereich möglich, da Vergleichsmaßstäbe nicht in beliebiger Größe hergestellt werden können. Die kleinsten Maßstäbe werden mit lithografischen Methoden erzeugt und sind nur wenige Mikrometer groß. Sie können unter einem Mikroskop wie ein normales Maßband benutzt werden oder werden mit optischen Vorrichtungen automatisiert abgelesen (s. Glasmaßstab). Die längsten Maßstäbe werden aus flexiblem Stahlband in Längen bis über 100 Meter hergestellt.

Alle diese Maßstäbe werden auf ein Längennormal (früher das Urmeter, heute die Definition des Meter mithilfe der Licht-Laufzeit) zurückgeführt. Diesen Prozess bezeichnet man als Kalibrierung. Die Definition des Meters ermöglicht die weltweite Vergleichbarkeit von Längenmessungen.

Rechentechnisch ist die direkte Entfernungsmessung als Schrägstrecke zu behandeln, die für ihre Umrechnung in eine horizontalen Strecke noch die Messung ihrer Neigung oder des Höhenwinkels erfordert.

Im Folgenden werden einige Verfahren der direkten Entfernungsmessung aufgeführt und kurz erläutert.

Interferometrie

Die Interferometrie mit kohärenten Wellen ist sehr präzise bei der Messung von Längenänderungen. Die Genauigkeit hängt im Wesentlichen von der benutzten Wellenlänge ab. In der Praxis werden Licht- und Radiowellen genutzt. Um mit einem Interferometer auch Entfernungen messen zu können, werden unter anderem das Phasenschiebeverfahren, die Weißlichtinterferometrie oder auch die konoskopische Holografie eingesetzt. Die Interferometrie ist eine direkte Messtechnik, da die zu bestimmende Entfernung mit der Wellenlänge des eingesetzten Lichtes verglichen wird. Die Wellenlänge ist an das internationale Einheitensystem angebunden.

Konfokale Abstandsmessung

Die Konfokaltechnik wird in verschiedenen technischen Ausführungen genutzt, um sehr kleine Abstände im Nanometer- bis Millimeterbereich zu bestimmen. Sie basiert auf dem Effekt der Tiefendiskriminierung: Ein Konfokalsensor liefert ein Signal, das umso größer ist, je näher sich das Messobjekt an der Fokusebene der Optik befindet. Die Konfokaltechnik ist eine direkte Messung, da sie Objekt oder Optik um die Messlänge verschiebt und die Verschiebung mit einem Referenzmaßstab vergleicht.

Indirekte Messung

Die direkte Messung kann in vielen Fällen nicht eingesetzt werden. Schon bei der Bestimmung des Abstandes zweier Inseln vom Festland aus scheitert sie, da die beiden Punkte nicht gleichzeitig zugänglich sind. Universeller und meist auch komfortabler einzusetzen sind indirekte Methoden.

Alle indirekten Methoden haben gemeinsam, dass sie nicht die Entfernung selbst messen, sondern eine von ihr abhängige Größe – beispielsweise die Laufzeitmessung eines Signals oder Echos (Laser, Radar), die Richtung einer Peilung oder die Helligkeit eines Sterns. Indirekt werden auch alle Änderungen der Entfernung gemessen, etwa mittels Dopplereffekt (siehe auch Annäherung). Indirekte Messungen müssen durch den Vergleich mit bekannten Maßstäben kalibriert werden, damit die Vergleichbarkeit mit anderen Messungen gewährleistet bleibt.

Hodometrie

Messrad

Kurvimeter

Die Hodometrie, oft auch nach dem Englischen als Odometrie bezeichnet, ist eine sehr einfache und alte Methode der indirekten Wegmessung, die eingeschränkt auch für die Entfernungsmessung verwendet werden kann. Dabei werden die Umdrehungen eines Rades mit bekanntem Umfang gezählt, das auf der Messstrecke abgerollt wird. Die Anzahl der Umdrehungen, multipliziert mit dem Umfang ergibt die gemessene Wegstrecke. Im Alltag wird diese Methode beispielsweise für Kilometerzähler von Autos oder Messrädern in der Vermessung eingesetzt.
(Siehe auch: Kurvimeter, Gerät zur Messung von kurvigen Wegstrecken in Landkarten)

Inertialnavigation

Inertialnavigation baut darauf auf, dass eine Bewegung, die nicht gleichförmig ist, immer mit einer Beschleunigung des bewegten Objektes verbunden ist. Integriert man alle Beschleunigungen, die ein Objekt erfahren hat, richtungsabhängig über der Zeit, kann man daraus nach der einfachen Formel Geschwindigkeit gleich Beschleunigung mal Zeit und Weg gleich Geschwindigkeit mal Zeit die zurückgelegte Wegstrecke berechnen (zweimalige numerische Integration). Dieses Verfahren setzt man in Fahr- und Flugzeugen aller Art ein, um eine umgebungsunabhängige Wegmessung zu ermöglichen. Allerdings summieren sich über der Zeit auch die Messfehler auf, weshalb die Position in regelmäßigen Abständen mit Informationen aus anderer Quelle abgeglichen werden muss.

Triangulation

Prinzip der Triangulation

Bei der dreifachen Angulation oder Triangulation peilt man den gesuchten Messpunkt von mindestens zwei verschiedenen Standorten mit bekanntem Abstand mit Hilfe eines Theodoliten oder eines anderen Winkelmessers an. Der Objektpunkt P und die beiden Standpunkte (1 und 2) bilden ein Dreieck, dessen Basislänge $ b $ und dessen Basiswinkel $ \alpha $ und $ \beta $ man kennt. Damit kann man alle anderen Größen im Dreieck berechnen. Die Basislänge bildet dabei den Maßstab der Triangulation. Die drei Winkel des Dreiecks geben der Methode den Namen 'Triangulation'.

In Umkehrung dieses Verfahrens können auch die Endpunkte einer hochgenauen Referenzstrecke, einer sogenannten Basislatte von einem Punkt aus angepeilt werden. Die Basislatte bildet damit die Basislänge eines gleichschenkligen Dreiecks.

Bereits im Altertum wurde die Triangulation zur Landvermessung eingesetzt und wird bis auf technische Neuerungen auch heute noch dafür verwendet. Hinzugekommen sind Verfahren der optischen Messtechnik wie die Streifenprojektion und die Photogrammetrie, die andere Anwendungsbereiche erschlossen haben.

Das Messverfahren selbst benutzt direkte (optische) oder indirekte (funktechnische) Winkelmessungen, messtechnisch jeweils als Phasenvergleiche (mehrdeutig) bei bekannter Länge der Messbasis realisiert. Aus der räumlichen Lage jeweils zweier Winkel kann der Abstand zur Basis bekannter Länge berechnet werden. Auch Abstandssensoren nutzen das Prinzip der Triangulation (siehe Lasertriangulation bzw. Abstandsmessung (optisch)). Eine einfache Variante zur Schätzung von Entfernungen ohne technische Hilfsmittel ist der Daumensprung; er setzt nur voraus, dass man die ungefähre Größe des Zielobjektes kennt.

Trilateration

Die Trilateration ist ein der Triangulation vergleichbares Verfahren, das ebenfalls drei Größen eines Dreiecks zu dessen Beschreibung benutzt, nämlich dessen Seiten. Daraus lassen sich wiederum alle anderen Größen berechnen, die das Dreieck definieren.

Das Messverfahren selbst benutzt direkte (optische) oder indirekte (funktechnische) Entfernungsmessungen, messtechnisch jeweils als Laufzeitmessungen (eindeutig) oder zusätzlich durch Phasenvergleiche (mehrdeutig) realisiert. Aus der räumlichen Lage zweier Punkte kann auf Grund geometrischer Beziehungen im Dreieck ihr Abstand berechnet werden. Die Methode dient vornehmlich dazu, die räumliche Lage von Messpunkten zueinander auf der Basis von einfachen Abstandsmessungen schnell und mit hinreichender Genauigkeit zu bestimmen.

Für die Bestimmung der Lage eines unbekannten Punktes im dreidimensionalen Raum sind vier bekannte Punkte erforderlich, auf einer Fläche genügen drei bekannte Punkte und entlang einer Trajektorie genügen zwei bekannte Punkte. Kann zwischen mehreren mathematisch korrekten Lösungen anhand von Nebenbedingungen ausgewählt werden, lässt sich die Zahl der notwendigen bekannten Punkte um die Zahl der nutzbaren Nebenbedingungen reduzieren.

Die Trilateration ist die Grundlage der Entfernungsmessung beispielsweise in Systemen der Satellitennavigation oder in Global Navigation Satellite Systems. Im Sinne der klassischen Geodäsie ist die Trilateration kein eigenständiges Vermessungsverfahren, wohl hingegen in der Satellitengeodäsie (siehe auch Satellite Laser Ranging und SECOR).

Laufzeitmessung

Prinzip der Laufzeitmessung

Die Laufzeitmessung beruht darauf, dass sich elektromagnetische und akustische Wellen mit endlicher, bekannter Geschwindigkeit ausbreiten. Sendet man ein Signal zu einem Messobjekt, von dem es reflektiert wird, und misst die Zeit, die es für den Hin- und Rückweg benötigt, so kann man aus der Laufzeit $ \Delta t $ und der Ausbreitungsgeschwindigkeit $ c $ des Signals, das ist die Gruppengeschwindigkeit der Welle, die Objektentfernung $ r $ berechnen:

$ r={\frac {c\cdot \Delta t}{2}} $

Die Messungen werden von der Umgebung beeinflusst. Wird ein Medium durchdrungen, wird die Lichtgeschwindigkeit gegenüber der Lichtgeschwindigkeit im Vakuum reduziert. Sind die Materialeigenschaften temperaturabhängig oder anisotrope Tensoren, werden Messungen der Laufzeit von Änderungen der Parameter oder der Orientierung gestört. Beispielsweise ist die Schallgeschwindigkeit stark temperaturabhängig, elektromagnetische Wellen werden von elektrisch leitenden Schichten der Atmosphäre abgelenkt.

Besonders problematisch ist die Bestimmung des Laufweges: Nur direkte Laufwege liefern die direkte Distanz. Alle Umwege über sekundäre Reflektoren liefern längere Laufzeiten und damit falsche Messdaten.

Beispiele:

• Fledermäuse und Ultraschall-Distanzsensoren bzw. -messgeräte nutzen Ultraschallsignale, um die Entfernung von Hindernissen und Beutetieren zu bestimmen.
• Das Echolot und das Sonar nutzen Schallsignale im Wasser für die Tiefenmessung unter Schiffen, für die Entfernungsmessung unter Wasser (U-Boote) und für die Ortung von Fischschwärmen.
• Radaranlagen nutzen elektromagnetische Wellen im Funkwellenlängenbereich zur Entfernungsmessung. Dabei unterscheidet man zwischen Impulsgeräten für große und Dauerstrichradargeräten für geringe Entfernungen. Siehe z. B. Distance Measuring Equipment, Satellitennavigation (z. B. GPS), Zeitbereichsreflektometrie
• Auch Licht ist für dieses Verfahren geeignet, siehe Satellite Laser Ranging, LIDAR, Laserpistole, Abstandsmessung (optisch).

Chromatisch-konfokale Abstandsmessung

Die chromatisch-konfokale Abstandsmessung nutzt die Dispersion von weißem, also spektral breitbandigem Licht in einem optischen System zur Bestimmung des Abstands zwischen Messobjekt und Sensor. Zur Messung dienen dabei die aufgrund der Dispersion in der Fokuslinse unterschiedlichen Brennweiten für verschiedene spektrale Anteile des Sensorlichts.

Kapazitive Abstandsmessung

Die Entfernung zwischen zwei leitfähigen Teilen kann anhand der zwischen ihnen bestehenden Kapazität bestimmt werden. Dazu müssen die Teile voneinander isoliert sein; sie werden zur Kapazitätsmessung in einen elektrischen Schwingkreis oder einen Ringoszillator einbezogen, dessen Frequenz empfindlich von der Kapazität abhängt. Anwendung finden sich bei der Fokuslageregelung an Laser-Schneidemaschinen, zur Positionsregelung in Nanopositioniersystemen und zur Kraftmessung.

Parallaxe

Zur Bestimmung von Entfernungen, die über den Maßstab des Sonnensystems hinausgehen, werden verschiedene Parallaxenmethoden verwendet. Das Wort „Parallaxe“ wird hier im Sinne von „Entfernung“ gebraucht. Man unterscheidet dabei zwischen den folgenden:

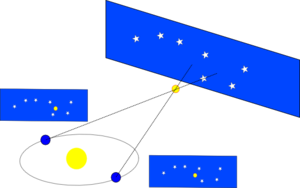
Trigonometrische Parallaxe

Entstehung der Parallaxe beim Umlauf der Erde um die Sonne

Die trigonometrische Parallaxe ist die Veränderung der Blickrichtung zu einem Objekt gegenüber dem Himmelshintergrund, der durch die jährliche Bewegung der Erde um die Sonne hervorgerufen wird. Die trigonometrische Parallaxe basiert somit auf der Triangulation, ihre Basislänge ist der Durchmesser der Erdbahn. Darüber hinaus spricht man auch von der täglichen Parallaxe, die durch die Rotation der Erde hervorgerufen wird. Je weiter das Objekt entfernt ist, desto kleiner ist die Parallaxe. Aus ihr lässt sich direkt die Entfernung berechnen:

$ r=1/\pi $

wobei hier die Entfernung r in Parsec (pc) und die Parallaxe $ \pi $ in Bogensekunden angegeben ist.

Die erste Parallaxenmessung eines Sterns konnte 1838 von Friedrich Wilhelm Bessel für den Stern 61 Cygni durchgeführt werden. Er bestimmte einen Wert von etwa 0,3 Bogensekunden und somit eine Entfernung von etwa 3,3 pc. Proxima Centauri, der Stern, der der Erde am nächsten ist, hat eine Parallaxe von 0,762 Bogensekunden, was einer Entfernung von etwa 1,31 pc entspricht. Normalerweise lässt sich die trigonometrische Parallaxe bis zu Entfernungen von etwa 100 pc bestimmen. Mit modernen Methoden sind heute aber auch schon Parallaxen von einigen Millibogensekunden gemessen worden. Zwischen 1989 und 1993 hat der Satellit Hipparcos etwa 100.000 Sterne bis zu einer Helligkeit von 9 mag vermessen und ihre Parallaxen bestimmt. Er erreichte dabei einen Fehler von nur 0,001 Bogensekunden. Die bisher (2005) kleinste Parallaxe konnte für den Pulsar PSR B1508+55 mit einem Radioteleskop bestimmt werden: sie betrug 0,415 Millibogensekunden (=0,000415 Bogensekunden) – das entspricht einer Entfernung von rund 2.400 pc oder etwa 7.800 Lichtjahren.^[1]

Spektroskopische Parallaxe

Bei der spektroskopischen oder photometrischen Parallaxe wird nicht wie bei der trigonometrischen Parallaxe die Richtung des Lichtes untersucht, sondern die Qualität. Neben der Temperatur eines Sterns hängt die Intensität des auf der Erde ankommenden Lichts natürlich auch von der Entfernung ab, wodurch es auch möglich ist, die Entfernung zu messen. Natürlich ist die Helligkeit eines Sternes, die direkt beobachtet werden kann, nur die sogenannte scheinbare Helligkeit m. Ein sehr heller Stern, der weit entfernt ist, und ein sehr naher Stern, der aber nur schwach leuchtet, können einem irdischen Beobachter beide gleich hell erscheinen. Deswegen ist es notwendig, die absolute Helligkeit M zu definieren: sie entspricht der scheinbaren Helligkeit, die ein Objekt hätte, wenn es genau 10 pc von der Erde entfernt wäre. Zwischen scheinbarer und absoluter Helligkeit besteht folgender Zusammenhang:

$ m-M=-5+5\cdot \log r $

wobei die Entfernung r in Parsec angegeben werden muss. Ist die absolute Helligkeit eines Objekts bekannt, lässt sich die Entfernung sofort aus der gemessenen scheinbaren Helligkeit berechnen. Die absolute Helligkeit lässt sich durch den Vergleich von Spektren bestimmen. Dabei wird das Spektrum des Objekts mit bekannter Entfernung als Maßstab verwendet – d. h. die spektroskopische Parallaxe baut direkt auf der trigonometrischen Parallaxe auf.

Dynamische Parallaxe

Die dynamische Parallaxe wird zur Entfernungsbestimmung von visuellen Doppelsternen verwendet. Dazu muss die Bahngeschwindigkeit $ v $, die sich spektroskopisch ermitteln lässt, bekannt sein; aus dem scheinbaren Abstand der beiden Sterne $ a $ und der Umlaufperiode $ T $ der Sterne um ihren Massenmittelpunkt kann man nun die Entfernung $ r $ berechnen.

Rotverschiebung

Die Entfernungsbestimmung mit Hilfe der Rotverschiebung des Lichts wird bei sehr weit entfernten Objekten wie Galaxien oder Quasaren angewandt. Für diese Entfernungen stehen keine alternativen Messverfahren zur Verfügung. Für die Rotverschiebung müssen bekannte Spektrallinien im Spektrum einer Galaxie identifiziert werden und ihre genaue Wellenlänge vermessen werden. Die Entfernung $ r $ lässt sich mittels der Hubble-Konstante $ H_{0} $ mit der folgenden Formel berechnen:

$ r={\frac {z\cdot c}{H_{0}}} $

wobei $ z={\frac {\lambda _{\text{beobachtet}}-\lambda _{0}}{\lambda _{0}}} $ die Rotverschiebung und $ c $ die Vakuumlichtgeschwindigkeit sind.

Anwendungen

Für jeden Entfernungsbereich werden geeignete Messmittel benötigt. Im Folgenden wird ein Überblick über die verschiedenen Anwendungen der Entfernungsmessung gegeben.

Entfernungsmessung im Alltag

Internationaler Meterprototyp, Standardbarren aus Platin-Iridium. Dies waren die Längennormale (Urmeter) bis 1960. (NIST)

Die direkte Messung ist die gebräuchlichste Methode der Entfernungsmessung im Alltag. Man vergleicht die zu messende Entfernung mit einem Vielfachen des Längennormals. Das erfolgt üblicherweise nicht mit einem Replikat des rechts dargestellten Urmeters, sondern mit einem preiswerten und handlichen Gliedermaßstab, Maßband oder Lineal. Mit diesen Messmitteln können auch längere Strecken bestimmt werden, indem man die Maßstäbe mehrfach hintereinander setzt. Dadurch vergrößert sich natürlich auch der Messfehler. Für sehr kleine Längen im Alltag von 0,1 Millimeter bis 200 Millimeter verwendet man mechanische Präzisionsmessinstrumente wie Messschieber oder Mikrometerschrauben. An unzugänglichen Stellen z. B. zwischen Maschinenteilen können auch deformierbare Wachsstreifen, sogenannte Plastigauges eingesetzt werden.

Zurückgelegte Wegstrecken

Die Entfernungsmessung auf gefahrenen Wegstrecken erfolgt meist mit einem Hodometer, der durch Zählung der Radumdrehungen die Strecke ermittelt. Solche Kilometerzähler sind bei Kraftfahrzeugen und Fahrrädern üblich. Das Verfahren impliziert zwar Ungenauigkeiten von bis zu einigen Prozent der Wegstrecke (z. B. hat ein abgefahrener Autoreifen einen etwas kleineren Durchmesser als ein neuer); für einfache Berechnungen zur Navigation oder des Treibstoffverbrauches reicht es aber aus. Genauere Messungen ermöglicht ein sogenanntes Peiselerrad. Für einfache geodätische Messungen wird die Hodometrie mit einem Messrad praktiziert. Für Wanderer gibt es Pedometer (Schrittzähler). In jüngerer Zeit verbreiten sich im Kraftfahrzeug, bei Wanderern und Radfahrern GPS-basierte Navigationssysteme, die Wegstrecken messen und aufzeichnen können. Spezielle Systeme können auch Höhenprofile messen und aufzeichnen, was für Bergwanderer, Radfahrer und Mountainbiker von Interesse sein kann. Auch Drachenflieger, Segelflieger und Gleitschirmflieger verwenden solche Systeme.

Je steiler eine zurückgelegte Wegstrecke ist, desto größer ist die Abweichung zwischen der tatsächlichen und der vom GPS-System angezeigten Strecke (für letztere findet sich die Bezeichnung Pseudo distance; ein deutsches Synonym hat sich wohl noch nicht etabliert).

Bezeichnungen am rechtwinkligen Dreieck

Dazu ein Zahlenbeispiel mit dem Satz des Pythagoras

(Sind $ a $, $ b $ und $ c $ die Seitenlängen eines rechtwinkligen Dreiecks, wobei $ a $ und $ b $ die Längen der Katheten und $ c $ die Länge der Hypotenuse ist, so gilt $ a^{2}+b^{2}=c^{2} $.)

Die Strecke b sei 4 Längeneinheiten; die Strecke a sei 3 LE. Dann ist c 5 LE lang. Die Strecke c sei eine steile Passstraße. Ein Navigationssystem behauptet, der Verkehrsteilnehmer habe nur 4 LE zurückgelegt: die von ihm für Rechenzwecke genutzte Landkarte ist plan, das heißt, sie ignoriert die zurückgelegten Höhenunterschiede und damit auch die dadurch entstehenden Wegverlängerungen (im Zahlenbeispiel: 5 LE statt 4 LE).

Landvermessung

Bei Strecken von einigen Kilometern, wie man sie in der Landesvermessung bestimmen muss, greift man zur geodätischen Triangulation. Hierbei entscheidet die Genauigkeit der Winkelmessung und die Länge des Vergleichsmaßstabes über die erreichbare Messgenauigkeit. Ein Triangulationsnetz kann eine relative Genauigkeit von einem Millionstel (0, 000 001) der gemessenen Länge besitzen. Eine Vermessung von Deutschland, das von Nord nach Süd rund 1000 Kilometer lang ist, würde also einen Fehler von rund einem Meter aufweisen. Zusätzlich muss aber noch der Maßstabsfehler berücksichtigt werden, der durch den Referenzmaßstab eingeführt wird.

Triangulatorische Abstandssensoren arbeiten nach dem Prinzip der Lasertriangulation, oft wird bei geringen Anforderungen hier auch eine Leuchtdiode als Strahlquelle eingesetzt.

Flugentfernungen

Radaranlage

Mit Radarwellen können Entfernungen zwischen wenigen Zentimetern und mehreren Millionen Kilometern gemessen werden, weshalb sie häufig in der Luftfahrt eingesetzt werden. Die Antenne sendet kurze Impulse bei einer Frequenz von einigen Gigahertz ($ 10^{9} $ Hertz) und misst die Zeit bis zum Empfang des vom Messobjekt reflektierten Signals. Neben der Entfernung können auch noch die Geschwindigkeit und die Richtung des Objektes gemessen werden.

Statt Funkwellen kommen auch verschiedene Arten der optischen Abstandsmessung zum Einsatz. Es kommen Blitzlampen, Laser und Leuchtdioden zum Einsatz. Beispiele sind die Wolkenhöhenmessung mit reflektierten Blitzsignalen einer Blitzlampe, die Laserpistole sowie LIDAR und die Lasertriangulation, die bei geringen Anforderungen auch mit einer Leuchtdiode arbeitet.

Unter Wasser und in der Erde

Entfernungen unter Wasser bestimmt man meist mit Schallwellen, beispielsweise mit einem Sonar oder Echolot. Für seismografische Untersuchungen innerhalb der Erde verwendet man u. a. Druckluft-Impulsschallquellen oder Sprengladungen und bestimmt die Laufzeiten zu mehreren Mikrofonen.

Fotografie

Leica I-Kleinbildkamera (1927) mit in den Zubehörschuh eingeschobenem Entfernungsmesser

In der Fotografie ist es notwendig, das verwendete Objektiv auf die korrekte Entfernung zum Motiv einzustellen. Es existiert eine Vielzahl von Ansätzen, dieses Problem technisch umzusetzen. Für die Bestimmung des Aufnahmeabstandes werden häufig optische Entfernungsmesser eingesetzt. Viele sind direkt in den Sucher eingebaut oder werden ins Sucherbild eingespiegelt.

Mikro- und Nanometerbereich

Die sichtbare Welt ist durch die Wellenlänge des Lichts beschränkt. Dinge, die kleiner sind als etwa die halbe Lichtwellenlänge von rund 0,5 Mikrometer, sind nicht mehr direkt beobachtbar. Bis zu dieser Grenze kann man aber noch sehr gut direkte Messungen vornehmen. Dazu verwendet man Messmikroskope für vertikale Messungen oder Messokulare für laterale Messungen sowie mikroskopische Maßstäbe, sogenannte Objektmikrometer, die man direkt mit der Objektgröße vergleicht.

Die optische Abstandsmessung bietet viele verschiedene Verfahren, die im Bereich bis ein Mikrometer und sogar deutlich darunter praktikabel sind. Das Phasenschiebeverfahren ermöglicht Abstandsmessungen bis zu einem Hundertstel der Lichtwellenlänge und wird in Interferometern oder Weißlichtinterferometern eingesetzt.

Atome und Elementarteilchen

Atome und Elementarteilchen füllen den Raum unterhalb von einem Nanometer ($ 10^{-9} $ Meter). Die Größe von Atomen und Elementarteilchen bestimmen die Physiker mit Hilfe von Streuexperimenten oder ausgefeilten Instrumenten wie Rasterkraftmikroskopen. Geht es aber um kleine Längenänderungen, auch bei sehr großen Referenzstrecken, so lassen sich die Methoden der Interferometrie so weit verfeinern, wie das beim GEO600-Experiment geschehen ist, das damit einer Genauigkeit von nur $ 6\cdot 10^{-19} $ Metern bei einer Referenzstrecke von 600 Metern zu den genauesten Messinstrumenten der Welt gehört.

Sonnensystem

Für sehr große, über die Erde hinausreichende Entfernungen hat die Astronomie eine große Fülle von Messverfahren entwickelt, die teilweise auf sehr spezielle Anwendungsfälle zugeschnitten sind:

Entfernung des Mondes

Der Laser-Reflektor, der von der Apollo-11-Besatzung auf dem Mond stationiert wurde (NASA).

Das 2,7-Meter-Harlan-J.-Smith-Teleskop des McDonald-Observatoriums (USA) wird benutzt, um mit einem Laser die auf dem Mond stationierten Reflektoren anzumessen. (Credit: McDonald Observatory)

Der Mond nimmt bei der Entfernungsmessung unter den Himmelskörpern im Sonnensystem eine Sonderstellung ein.

Seit etwa 1900 ist die große Halbachse der Mondbahn mit etwa 384.000 km bekannt, um 1965 wurde der Wert – auch aufgrund genauerer Erdparameter durch die Satellitengeodäsie – auf 384.400 km korrigiert ^[2]. Inzwischen können langfristige Veränderungen der Mondbahn sogar auf wenige Dezimeter erfasst werden.

Seit der ersten Mondlandung 1969 ist eine äußerst exakte Entfernungsbestimmung möglich. Von der Besatzung der Apollo 11 wurde damals eine Anordnung von Retroreflektoren, das sogenannte lunar laser ranging retroreflector array, auf der Mondoberfläche im Mare Tranquillitatis aufgestellt (siehe Bild). Dadurch ist es möglich, die Entfernung des Mondes auf wenige Zentimeter genau zu bestimmen. Dazu wird von der Erdoberfläche ein Laserstrahl ausgesandt (siehe Bild), der genau auf den Reflektor auf der Mondoberfläche gerichtet ist. Durch dessen Struktur wird der Laserstrahl wieder exakt zum Sender zurückgeworfen. Im Normalfall kommen vom ausgesandten Signal nur wenige Photonen, manchmal sogar nur ein einziges, zurück, die dort detektiert werden können. Aus der Zeit, die zwischen Aussendung und der Rückkehr des reflektierten Signals vergeht, lässt sich dann die Entfernung genau bestimmen.^[3]

Neben dem Reflektor der Apollo-11-Mission wurden später noch vier weitere Laserspiegel auf der Mondoberfläche aufgestellt: Zwei durch die NASA während der Apollo-14-Mission (1971 nördlich des Kraters Fra Mauro) und der Apollo-15-Mission (1971 östlich an der Hadley-Rille); zusätzlich enthielten die beiden sowjetischen Lunochod-Mondfahrzeuge je einen Laser-Reflektor, doch anders als bei Lunochod 2, das 1973 während der unbemannten Mondmission Luna 21 im Mondkrater Le Monnier stationiert wurde, konnte vom Reflektor von Lunochod 1 im Rahmen der unbemannten Luna-17-Mission nach Abschluss der Aktivitäten 1970/1971 im Mare Imbrium über Jahrzehnte kein Laserecho mehr empfangen werden. Im März 2010 wurden Luna 17 und Lunochod 1 schließlich auf Aufnahmen der Sonde Lunar Reconnaissance Orbiter entdeckt. Dadurch wurde auch eine Berechnung der Parkposition möglich: 38,2473° N; 325,002° E für Luna 17 und 38,32507° N; 324,9949° E für Lunochod 1.^[4] Nach der Neuberechnung der Parkposition konnte der Reflektor wieder benutzt werden.^[5][6] Am 22. April 2010 wurden vom Apache-Point-Observatorium erfolgreich Lasermessungen durchgeführt.^[7]

Durch die seit mehr als 35 Jahren andauernden Messungen konnte nicht nur die Mondentfernung äußerst exakt bestimmt werden, sondern es wurden auch Erkenntnisse auf vielen anderen Gebieten gewonnen. So konnte z. B. festgestellt werden, dass sich der Mond um etwa 3,8 cm pro Jahr von der Erde entfernt.^[8] Grund dafür ist die Gezeitenreibung, die den Drehimpuls der Erde verringert. Durch die genaue Messung des Abstandes konnte auch der numerische Wert der Gravitationskonstanten sehr genau errechnet werden. Seit Beginn der Messungen unterscheiden sich die so bestimmten Werte nur um einen Faktor von $ 10^{-10} $. Auch die Gültigkeit der allgemeinen Relativitätstheorie ließ sich durch die exakten Abstandsmessungen bestätigen. 2003 wurde die APOLLO (Apache Point Observatory Lunar Laser-ranging Operation) gegründet: Mit dem 3,5-Meter-Teleskop der Apache-Point-Sternwarte in New Mexico liegt seit 2006 die Genauigkeit der bisher gesammelten Daten im Millimeterbereich.^[9]

Radarmessungen

Für die inneren Planeten Merkur, Venus und Mars sowie die Asteroiden können die Astronomen aktive Laufzeitmessungen verwenden. Dabei greifen sie auf eine verfeinerte Radar-Entfernungsmessung zurück. Bei weiter entfernten Objekten versagt das aber, da die Signallaufzeit zu lange und die reflektierte Energie zu klein wird.

Die Milchstraße

Bei Entfernungen, die über das Sonnensystem hinausreichen, hilft zunächst ein Verfahren, das auch in der Landvermessung gebräuchlich ist: Die Triangulation, die in der Astronomie als Trigonometrische Parallaxe bezeichnet wird. Mit ihr sind Entfernungen bis zu $ 10^{19} $ Meter bestimmbar. Das genügt, um die Entfernung der benachbarten Regionen der Milchstraße zu vermessen.

Die Galaxien und das Weltall

Für Entfernungen über 1 Zetameter (rund 100 000 Lichtjahre), jenseits der Milchstraße, benutzen die Astronomen die fotometrische Parallaxe. Um diese Verfahren zu kalibrieren, werden sogenannte „Standardkerzen“ verwendet. Das sind Sterne, die eine bekannte absolute Helligkeit besitzen, aus der sich dann durch Messung der scheinbaren Helligkeit die Entfernung bestimmen lässt. Bekannt ist die absolute Helligkeit beispielsweise bei den Cepheiden, da bei ihnen die so genannte Perioden-Leuchtkraft-Beziehung besteht.

Die Entfernung von Kugelsternhaufen kann mittels ihrer Farbe und Helligkeit und dem Farben-Helligkeits-Diagramm bestimmt werden.

Um schließlich die Ausdehnung des Universums zu vermessen, wird die Rotverschiebung der Galaxien bestimmt. Mit ihr wird ein Bereich bis rund $ 10^{26} $ Meter erfasst.

Quellen

Literatur

• Fritz Deumlich, Rudolf Staiger: Instrumentenkunde der Vermessungstechnik, 9. Aufl., Wichmann, Heidelberg, 2001, ISBN 3-87907-305-8
• Walter Grossmann: Winkel- und Streckenmessgeräte, de Gruyter, Berlin – New York 1983, ISBN 3-11-009601-3
• Karl Kraus: Photogrammetrie. de Gruyter, 2004, ISBN 3-11-017708-0
• Thomas Luhmann: Nahbereichsphotogrammetrie. Wichmann, Heidelberg, 2003, ISBN 3-87907-398-8
• McGlone, Mikhail, Bethel (Hrsg.): Manual of Photogrammetry, 5th edition. ASPRS, 2004, ISBN 1-57083-071-1
• Rudolf Sigl: Geodätische Astronomie, Wichmann, Karlsruhe 1975, ISBN 3-87907-041-5
• Hans Zetsche: Elektronische Entfernungsmessung, Konrad Wittwer, Stuttgart 1979, ISBN 3-87919-127-1

Weblinks

• Überblick über Methoden der Entfernungsmessung in der Astronomie