Modulationsübertragungsfunktion: Unterschied zwischen den Versionen
- Bildgebung
- Bildverarbeitung
imported>Summ (kein bildgebendes Verfahren für sich) |
imported>Bicycle Tourer K (Klammern korrigiert) |
||
| Zeile 1: | Zeile 1: | ||
Die '''Modulationsübertragungsfunktion''' (auch '''Modulationstransferfunktion''' (MTF, | Die '''Modulationsübertragungsfunktion''' (auch '''Modulationstransferfunktion''' (MTF, englisch ''Modulation Transfer Function'') oder '''Kontrastübertragungsfunktion''') ist die mathematische Beschreibung des Vergleiches zwischen dem [[Schärfe (Fotografie)#Kontrast|Detailkontrast]] an Kanten eines Objektes und dem Detailkontrast dessen bildlicher Darstellung. Es wird immer ein Detailkontrastverlust festgestellt. Dies ist nicht zu verwechseln mit dem Kontrast im allgemeinen Sprachgebrauch, wie er sich durch Bildbearbeitung (oder in der chemischen Fotografie z. B. durch die Wahl des Papiers) beliebig verändern, insbes. sogar über den Motiv-Originalkontrast hinaus erhöhen, lässt. | ||
[[ | [[Datei:Kontrastverlust.jpg|mini|360px|Durch das bildgebende System ([[Objektiv (Optik)|Objektiv]], [[Kamera]], [[Teleskop]], [[Fotolabor]], [[Dia (Fotografie)|Dia]] usw.) entsteht immer ein Detailkontrastverlust. Während beim gescannten Dia durch Bildbearbeitung der bildglobale Kontrast verringert wurde (hier nicht von Interesse), erkennt man im Hauptbild eine Schwächung des Detailkontrasts (insbes. der Äste im Himmels-Gegenlicht).]] | ||
== Prinzip == | == Prinzip == | ||
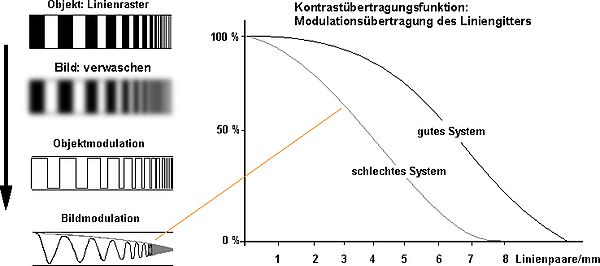
[[Datei:MBq MTF.jpg|mini|600px|Modulationsübertragungsfunktion, grafische Darstellung]] | |||
Das kontrastreiche Linienraster eines Objektes hat (siehe rechte Grafik) in der bildlichen Darstellung an Kontrast verloren (verwaschen). In der mathematischen Darstellung entspricht das Linienraster (des Objektes) einem eckigen Kurvenverlauf ''Objektmodulation''. | |||
Durch den Kontrastverlust verändert sich dieser Kurvenverlauf. Der neue Kurvenverlauf (des Bildes mit dem Kontrastverlust) wird idealisiert als [[Sinus und Kosinus|Sinuskurve]] dargestellt (Bildmodulation). | |||
Durch den Kontrastverlust verändert sich dieser Kurvenverlauf. Der neue Kurvenverlauf (des Bildes mit dem Kontrastverlust) wird idealisiert als [[ | |||
Mit [[Modulation (Technik)|Modulation]] ist in diesem Zusammenhang gemeint: | Mit [[Modulation (Technik)|Modulation]] ist in diesem Zusammenhang gemeint: | ||
* die mathematische Darstellung eines Signals (in diesem Fall eines optischen Signals). | * die mathematische Darstellung eines Signals (in diesem Fall eines optischen Signals). | ||
* die Veränderung des Signals (durch das [[ | * die Veränderung des Signals (durch das [[Bildgebendes Verfahren|bildgebende System]]). | ||
Beide Modulationen (Objekt- und Bildmodulation) werden miteinander verglichen. Das Ergebnis drückt die Höhe des Kontrastverlustes aus. | Beide Modulationen (Objekt- und Bildmodulation) werden miteinander verglichen. Das Ergebnis drückt die Höhe des Kontrastverlustes aus. | ||
Mit der ''Heynacher-Zahl'' (nach E. Heynacher von [[Carl Zeiss (Unternehmen)|Carl Zeiss]]) wird versucht, die Modulationsübertragungsfunktion auf das Sehvermögen des menschlichen Auges zu beziehen.<ref>E. Heynacher: ''Einige Bemerkungen zum Problem der Optischen Bildbeurteilung'' | Mit der ''Heynacher-Zahl'' (nach E. Heynacher von [[Carl Zeiss (Unternehmen)|Carl Zeiss]]) wird versucht, die Modulationsübertragungsfunktion auf das Sehvermögen des menschlichen Auges zu beziehen.<ref>E. Heynacher: ''Einige Bemerkungen zum Problem der Optischen Bildbeurteilung.'' In: Journal of Modern Optics, Volume 7, Issue 2 April 1960, S. 173–178.</ref> Eine andere psychophysikalisch begründete Größe ist SQF (''[[Subjective Quality Factor]]'').<ref>H. H. Nasse: ''[https://lenspire.zeiss.com/photo/app/uploads/2018/02/Article-MTF-Part1-2008-DE.pdf Wie liest man MTF-Kurven?]'' (PDF; 614 kB). In: Carl Zeiss, Geschäftsbereich Photo-Objektive, Dezember 2008.</ref> | ||
== Mathematische Beschreibung == | == Mathematische Beschreibung == | ||
<math>\mathrm{MTF}(f) = \frac{\mathrm{Bildkontrast}(f)}{\mathrm{Objektkontrast}(f)}</math> | <math>\mathrm{MTF}(f) = \frac{\mathrm{Bildkontrast}(f)}{\mathrm{Objektkontrast}(f)}</math> | ||
:mit ''f'', der [[Ortsfrequenz]] der Modulation. | : mit ''f'', der [[Ortsfrequenz]] der Modulation. | ||
Das Ergebnis ist ein [[ | Das Ergebnis ist ein [[Schärfe (Fotografie)#Das klassische Zählmaß|Zählmaß]] mit folgenden Eigenschaften: | ||
* Vorteil: Vergleichbarkeit von Messergebnissen | * Vorteil: Vergleichbarkeit von Messergebnissen | ||
* Nachteil: Die Messergebnisse setzen [[ | * Nachteil: Die Messergebnisse setzen [[Schärfe (Fotografie)#Definierte Randbedingungen|idealisierte Bedingungen]] voraus.<ref>"Die Schärfe des Röntgenbildes ist subjektiv definiert. Seit Anbeginn der klinischen Radiologie wurde immer wieder die Abbildung von Kanten zur Definition der Schärfe einer Abbildung herangezogen. Infolge unterschiedlicher Wirkungen der die Abbildung bestimmenden Einflüsse auf das Bild einer Kante konnten jedoch keine allgemein befriedigenden Kriterien aufgestellt werden. Grund dafür ist die Tatsache, dass der menschliche Sehprozess selbst einen Einfluss auf den Schärfeeindruck hat. Objektive Kriterien, die jedoch den Begriff der Schärfe nicht voll erfassen, sind das Auflösungsvermögen z. B. von Strichrastern oder besser die Modulationsübertragungsfunktion."<br />[http://download.sstmed.com/Tools/Aufnahmehelfer.pdf Handbuch Radiographie, Dr. Buchmann, 1996 (PDF-Datei; 3,6 MB)]</ref> | ||
== Spezifikationen == | == Spezifikationen == | ||
[[Datei:CSF1.png|mini|Die Modulationsübertragungsfunktion eines Betrachters kann mit einer [[zweidimensional]]en, [[sinus]]förmigen und [[Amplitudenmodulation|amplitudenmodulierten]] Objektvorlage abgeschätzt werden. Die Ortsfrequenz steigt in der originalen [[Bildauflösung]] (= 4096 × 4096 [[Pixel]]) von links nach rechts [[Logarithmische Darstellung|logarithmisch]] von 1 auf 2048 Linienpaare pro Bildbreite. Der Objektkontrast auf der untersten Linie beträgt 100 Prozent und nimmt nach oben [[Linearität|linear]] auf 0 Prozent ab. Die Kurve, bei der der Betrachter gerade noch Helligkeitsunterschiede wahrnehmen kann, wird durch die [[Kontrastempfindlichkeitsfunktion]] beschrieben (CSF = Contrast Sensitivity Function). Das menschliche Auge ist bei rund 200 Linienpaare pro Bildbreite am empfindlichsten.<ref>[[b:Digitale bildgebende Verfahren: Grundlagen#Kontrastempfindlichkeitsfunktion|Kontrastempfindlichkeitsfunktion]], Wikibook ''Digitale bildgebende Verfahren'', Kapitel ''Grundlagen'', abgerufen am 5. Juli 2018.</ref>]] | |||
Für den Vergleich der Modulationen (des Kontrastes) können verschiedene Objektmodulationen (= Kurvenverläufe) benutzt werden. Typische Muster sind der eckige Kurvenverlauf und die Sinuskurve. Durch die bildgebenden Systeme wird der gewählte Kurvenverlauf immer geändert. | Für den Vergleich der Modulationen (des Kontrastes) können verschiedene Objektmodulationen (= Kurvenverläufe) benutzt werden. Typische Muster sind der eckige Kurvenverlauf und die Sinuskurve. Durch die bildgebenden Systeme wird der gewählte Kurvenverlauf immer geändert. | ||
Andere Messvariationen berücksichtigen weitere Parameter. <ref>"… es kann einem passieren, dass man mit zwei Objektiven, die gleiche MTF-Daten haben, von einem Detail des Gegenstandes ganz verschiedene Bilder erhält." (zeiss.com: [ | Andere Messvariationen berücksichtigen weitere Parameter.<ref>"… es kann einem passieren, dass man mit zwei Objektiven, die gleiche MTF-Daten haben, von einem Detail des Gegenstandes ganz verschiedene Bilder erhält." (zeiss.com: [https://lenspire.zeiss.com/photo/app/uploads/2018/02/Article-MTF-Part1-2008-DE.pdf Wie liest man MTF-Kurven?])</ref> | ||
== Anwendungen == | == Anwendungen == | ||
In der Röntgendiagnostik muss die MÜF für die bildgebenden Systeme regelmäßig geprüft werden. Kenngrößen sind die ''Grenzauflösung'' (Ortsfrequenz, bei der die Modulation unter 2 % sinkt) und die ''charakteristische Modulation'' (Modulation in Prozent bei der Ortsfrequenz 1 Linienpaar/mm). | |||
Bei der Entwicklung von Linsensystemen oder Optiken ist die Berechnung und Optimierung der optischen Übertragungsfunktion essentiell und entscheidet über die Güte des Gerätes. Zur Vereinfachung dieser Entwicklungsarbeiten wird die MÜF meistens nicht mehr experimentell, sondern per Computermodell berechnet.<ref>zeiss.com: [https://lenspire.zeiss.com/photo/app/uploads/2018/02/Article-MTF-Part1-2008-DE.pdf Wie liest man MTF-Kurven?]</ref> Da es sich bei MÜF um idealisierte Werte handelt, tut das dem Grundprinzip – ein Vergleichswert zu sein – keinen Abbruch. | |||
Professionelle Kameras verfügen über aufwendige Linsensysteme, um bei hoher Lichtausbeute möglichst geringe Abbildungsfehler zu erzeugen, was mit der MÜF spezifiziert werden kann. Hat zum Beispiel das Objektiv einen sehr starken Abfall zu hohen Frequenzen hin (ähnlich dem Muster in der oberen Grafik), dann hilft es nicht, die Auflösung des Detektors zu steigern, um eine bessere [[Auflösung (Fotografie)|Auflösung]] zu erreichen. | |||
Professionelle Kameras verfügen über aufwendige Linsensysteme, um bei hoher Lichtausbeute möglichst geringe Abbildungsfehler zu erzeugen, was mit der MÜF spezifiziert werden kann. Hat zum Beispiel das Objektiv einen sehr starken Abfall zu hohen Frequenzen hin (ähnlich dem Muster in der oberen Grafik), dann hilft es nicht, die Auflösung des Detektors zu steigern, um eine bessere [[ | |||
Bei der Internetrecherche zu MÜF-Werten empfiehlt sich das Stichwort „Datenblatt“ (als zusätzlicher Suchbegriff). | Bei der Internetrecherche zu MÜF-Werten empfiehlt sich das Stichwort „Datenblatt“ (als zusätzlicher Suchbegriff). | ||
=== Hybridbilder === | === Hybridbilder === | ||
[[Datei:wikigolfball.jpg| | [[Datei:wikigolfball.jpg|mini|120px|Golfball als Hybridbild]] | ||
Bei [[Hybridbild]]ern wird bei der Überlagerung zweier ähnlicher Bilder mit Hilfe der Manipulation der Kontrastübertragungsfunktionen eine [[optische Täuschung]] hervorgerufen. | |||
Bei [[Hybridbild]]ern wird bei der Überlagerung zweier ähnlicher Bilder mit Hilfe der Manipulation der Kontrastübertragungsfunktionen eine [[ | |||
== Normen == | |||
* [[DIN 58185]], Optische Übertragungsfunktion | * [[DIN 58185]], Optische Übertragungsfunktion | ||
** Teil 1: Formelzeichen, Begriffe, mathematische Zusammenhänge | ** Teil 1: Formelzeichen, Begriffe, mathematische Zusammenhänge | ||
| Zeile 58: | Zeile 50: | ||
** Teil 3: Durchführung der Messung | ** Teil 3: Durchführung der Messung | ||
** Teil 4: Darstellung | ** Teil 4: Darstellung | ||
* [[ISO 11421]] (1997): Optik und optische Instrumente | * [[ISO 11421]] (1997): Optik und optische Instrumente – Genauigkeit von Messungen der optischen Übertragungsfunktion | ||
* [[ISO 15529]] (2010): Optik und Photonik | * [[ISO 15529]] (2010): Optik und Photonik – Optische Übertragungsfunktion – Messung der Modulationsübertragungsfunktion (MTF) von abtastenden Abbildungssystemen | ||
== Literatur == | |||
* Theodor Laubenberger: ''Technik der medizinischen Radiologie: Diagnostik, Strahlentherapie, Strahlenschutz.'' 7. Auflage. Deutscher Ärzteverlag, Köln 1999, ISBN 3-7691-1132-X. | |||
== Weblinks == | == Weblinks == | ||
| Zeile 66: | Zeile 61: | ||
* [http://www.trioptics.com/de/knowledgebase/mtf.php Grundlagen der MTF-Messung] | * [http://www.trioptics.com/de/knowledgebase/mtf.php Grundlagen der MTF-Messung] | ||
* [http://www.foto-net.de/net/objektive/test.html Modulationsübertragungsfunktion] | * [http://www.foto-net.de/net/objektive/test.html Modulationsübertragungsfunktion] | ||
* Markus Bautsch: [ | * Markus Bautsch: [[b:Digitale bildgebende Verfahren: Grundlagen#Modulationsübertragung|Modulationsübertragung]], in: Wikibooks ''Digitale bildgebende Verfahren – Grundlagen'' | ||
== Einzelnachweise == | |||
<references /> | |||
{{SORTIERUNG:Modulationsubertragungsfunktion}} | |||
[[Kategorie:Bildgebung]] | [[Kategorie:Bildgebung]] | ||
[[Kategorie:Bildverarbeitung]] | [[Kategorie:Bildverarbeitung]] | ||
Aktuelle Version vom 11. Januar 2021, 01:16 Uhr
Die Modulationsübertragungsfunktion (auch Modulationstransferfunktion (MTF, englisch Modulation Transfer Function) oder Kontrastübertragungsfunktion) ist die mathematische Beschreibung des Vergleiches zwischen dem Detailkontrast an Kanten eines Objektes und dem Detailkontrast dessen bildlicher Darstellung. Es wird immer ein Detailkontrastverlust festgestellt. Dies ist nicht zu verwechseln mit dem Kontrast im allgemeinen Sprachgebrauch, wie er sich durch Bildbearbeitung (oder in der chemischen Fotografie z. B. durch die Wahl des Papiers) beliebig verändern, insbes. sogar über den Motiv-Originalkontrast hinaus erhöhen, lässt.

Prinzip
Das kontrastreiche Linienraster eines Objektes hat (siehe rechte Grafik) in der bildlichen Darstellung an Kontrast verloren (verwaschen). In der mathematischen Darstellung entspricht das Linienraster (des Objektes) einem eckigen Kurvenverlauf Objektmodulation.
Durch den Kontrastverlust verändert sich dieser Kurvenverlauf. Der neue Kurvenverlauf (des Bildes mit dem Kontrastverlust) wird idealisiert als Sinuskurve dargestellt (Bildmodulation).
Mit Modulation ist in diesem Zusammenhang gemeint:
- die mathematische Darstellung eines Signals (in diesem Fall eines optischen Signals).
- die Veränderung des Signals (durch das bildgebende System).
Beide Modulationen (Objekt- und Bildmodulation) werden miteinander verglichen. Das Ergebnis drückt die Höhe des Kontrastverlustes aus.
Mit der Heynacher-Zahl (nach E. Heynacher von Carl Zeiss) wird versucht, die Modulationsübertragungsfunktion auf das Sehvermögen des menschlichen Auges zu beziehen.[1] Eine andere psychophysikalisch begründete Größe ist SQF (Subjective Quality Factor).[2]
Mathematische Beschreibung
$ \mathrm {MTF} (f)={\frac {\mathrm {Bildkontrast} (f)}{\mathrm {Objektkontrast} (f)}} $
- mit f, der Ortsfrequenz der Modulation.
Das Ergebnis ist ein Zählmaß mit folgenden Eigenschaften:
- Vorteil: Vergleichbarkeit von Messergebnissen
- Nachteil: Die Messergebnisse setzen idealisierte Bedingungen voraus.[3]
Spezifikationen

Für den Vergleich der Modulationen (des Kontrastes) können verschiedene Objektmodulationen (= Kurvenverläufe) benutzt werden. Typische Muster sind der eckige Kurvenverlauf und die Sinuskurve. Durch die bildgebenden Systeme wird der gewählte Kurvenverlauf immer geändert.
Andere Messvariationen berücksichtigen weitere Parameter.[5]
Anwendungen
In der Röntgendiagnostik muss die MÜF für die bildgebenden Systeme regelmäßig geprüft werden. Kenngrößen sind die Grenzauflösung (Ortsfrequenz, bei der die Modulation unter 2 % sinkt) und die charakteristische Modulation (Modulation in Prozent bei der Ortsfrequenz 1 Linienpaar/mm).
Bei der Entwicklung von Linsensystemen oder Optiken ist die Berechnung und Optimierung der optischen Übertragungsfunktion essentiell und entscheidet über die Güte des Gerätes. Zur Vereinfachung dieser Entwicklungsarbeiten wird die MÜF meistens nicht mehr experimentell, sondern per Computermodell berechnet.[6] Da es sich bei MÜF um idealisierte Werte handelt, tut das dem Grundprinzip – ein Vergleichswert zu sein – keinen Abbruch.
Professionelle Kameras verfügen über aufwendige Linsensysteme, um bei hoher Lichtausbeute möglichst geringe Abbildungsfehler zu erzeugen, was mit der MÜF spezifiziert werden kann. Hat zum Beispiel das Objektiv einen sehr starken Abfall zu hohen Frequenzen hin (ähnlich dem Muster in der oberen Grafik), dann hilft es nicht, die Auflösung des Detektors zu steigern, um eine bessere Auflösung zu erreichen.
Bei der Internetrecherche zu MÜF-Werten empfiehlt sich das Stichwort „Datenblatt“ (als zusätzlicher Suchbegriff).
Hybridbilder
Bei Hybridbildern wird bei der Überlagerung zweier ähnlicher Bilder mit Hilfe der Manipulation der Kontrastübertragungsfunktionen eine optische Täuschung hervorgerufen.
Normen
- DIN 58185, Optische Übertragungsfunktion
- Teil 1: Formelzeichen, Begriffe, mathematische Zusammenhänge
- Teil 2: Gerätegrundlagen
- Teil 3: Durchführung der Messung
- Teil 4: Darstellung
- ISO 11421 (1997): Optik und optische Instrumente – Genauigkeit von Messungen der optischen Übertragungsfunktion
- ISO 15529 (2010): Optik und Photonik – Optische Übertragungsfunktion – Messung der Modulationsübertragungsfunktion (MTF) von abtastenden Abbildungssystemen
Literatur
- Theodor Laubenberger: Technik der medizinischen Radiologie: Diagnostik, Strahlentherapie, Strahlenschutz. 7. Auflage. Deutscher Ärzteverlag, Köln 1999, ISBN 3-7691-1132-X.
Weblinks
- Hubert Nasse: Wie liest man MTF-Kurven? Teil 1 (PDF; 614 kB), Teil 2 (PDF; 296 kB), MTF-Bilder (ZIP; 28,8 MB), Carl Zeiss AG
- Erläuterung für MTF von Filmen und Linsen (englisch)
- Grundlagen der MTF-Messung
- Modulationsübertragungsfunktion
- Markus Bautsch: Modulationsübertragung, in: Wikibooks Digitale bildgebende Verfahren – Grundlagen
Einzelnachweise
- ↑ E. Heynacher: Einige Bemerkungen zum Problem der Optischen Bildbeurteilung. In: Journal of Modern Optics, Volume 7, Issue 2 April 1960, S. 173–178.
- ↑ H. H. Nasse: Wie liest man MTF-Kurven? (PDF; 614 kB). In: Carl Zeiss, Geschäftsbereich Photo-Objektive, Dezember 2008.
- ↑ "Die Schärfe des Röntgenbildes ist subjektiv definiert. Seit Anbeginn der klinischen Radiologie wurde immer wieder die Abbildung von Kanten zur Definition der Schärfe einer Abbildung herangezogen. Infolge unterschiedlicher Wirkungen der die Abbildung bestimmenden Einflüsse auf das Bild einer Kante konnten jedoch keine allgemein befriedigenden Kriterien aufgestellt werden. Grund dafür ist die Tatsache, dass der menschliche Sehprozess selbst einen Einfluss auf den Schärfeeindruck hat. Objektive Kriterien, die jedoch den Begriff der Schärfe nicht voll erfassen, sind das Auflösungsvermögen z. B. von Strichrastern oder besser die Modulationsübertragungsfunktion."
Handbuch Radiographie, Dr. Buchmann, 1996 (PDF-Datei; 3,6 MB) - ↑ Kontrastempfindlichkeitsfunktion, Wikibook Digitale bildgebende Verfahren, Kapitel Grundlagen, abgerufen am 5. Juli 2018.
- ↑ "… es kann einem passieren, dass man mit zwei Objektiven, die gleiche MTF-Daten haben, von einem Detail des Gegenstandes ganz verschiedene Bilder erhält." (zeiss.com: Wie liest man MTF-Kurven?)
- ↑ zeiss.com: Wie liest man MTF-Kurven?