Kraft und Drehmoment

Moment einer Kraft

Es ist schwierig, eine Mutter mit den Fingern festzuziehen. Aber mit einem Schraubenschlüssel hast du ein Werkzeug zur Hand, mit dem du dir das Leben erheblich erleichtern kannst.

Die Wirkung ist noch größer, wenn man die Kraft erhöht oder einen längeren Schraubenschlüssel benutzt. Die Drehwirkung einer Kraft wird in der Physik als Moment oder Drehmoment bezeichnet. Es wird wie folgt berechnet:

Moment = Kraft $\cdot$ Entfernung vom Drehpunkt

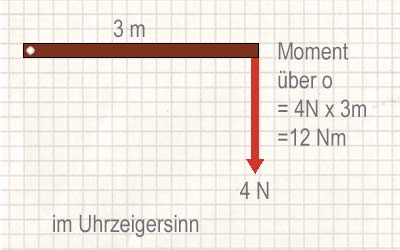
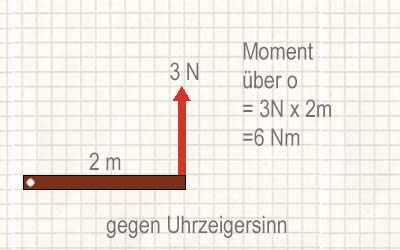
Unten werden einige Beispiele für Kräfte und ihre Drehmomente gezeigt. Drehmomente werden je nach ihrer Richtung im Uhrzeigersinn oder gegen den Uhrzeigersinn beschrieben.

Das Prinzip des Moments von Kräften

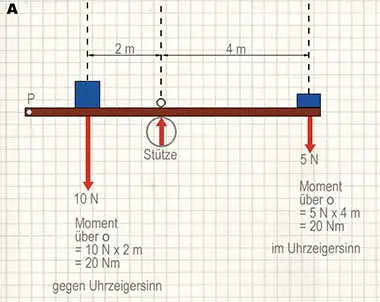
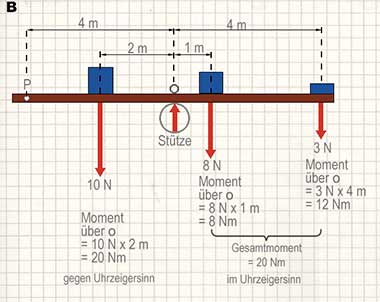
In Diagramm A (weiter unten) ist der Balken in einem Zustand des Gleichgewichts. Beachte, dass das Drehmoment um o gegen den Uhrzeigersinn gleich dem Drehmoment im Uhrzeigersinn ist. Eine Drehwirkung gleicht die andere aus. In Diagramm B wirken mehrere Kräfte, aber der Balken ist wiederum im Gleichgewicht. Diesmal ist das gesamte Drehmoment um o im Uhrzeigersinn gleich dem Drehmoment gegen den Uhrzeigersinn.

Diese Beispiele veranschaulichen das Prinzip der Momente. Wenn ein Objekt im Gleichgewicht ist, dann gilt:

Die Summe der Drehmomente um einen beliebigen Punkt im Uhrzeigersinn ist gleich der Summe der Drehmomente um diesen Punkt gegen den Uhrzeigersinn.

Gleichgewichtsbedingungen

Wenn ein Objekt im Gleichgewicht ist, müssen die Kräfte, die darauf wirken, genauso ausgeglichen sein wie ihre Drehmomente. Damit:

• Die Summe der Kräfte in einer Richtung muss der Summe der Kräfte in der entgegengesetzten Richtung entsprechen
• Das Prinzip der Momente muss gelten.

Zum Beispiel muss im Diagramm A die Aufwärtskraft vom Balken 15 N betragen, um die 10 N + 5 N Gesamtabwärtskraft auszugleichen. Auch wenn du die Drehmomente um irgendeinen Punkt bestimmst, zum Beispiel P, muss das gesamte Drehmoment im Uhrzeigersinn dem gesamten Drehmoment gegen den Uhrzeigersinn entsprechen.

Wenn du die Drehmomente um P bestimmst, musst du das Drehmoment der Aufwärtskraft vom Balken mit einschließen. Dies gilt aber nicht, wenn du das Drehmoment um O bestimmen willst, weil die Kraft kein Drehmoment um diesem Punkt hat.

Rechenbeispiel

Eine Person mit einem Gewicht von 500 N steht auf einem Brett, das auf zwei Böcken liegt. Berechne die Aufwärtskräfte X und Y, die von den Bünden auf das Brett wirken. (Wir vernachlässigen das Gewicht des Bretts)

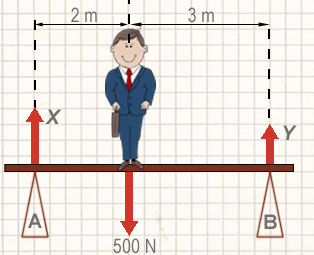
Das System ist im Gleichgewicht, also gilt das Prinzip der Drehmomente. Du kannst die Drehmomente um jeden Punkt bestimmen. Aber bei der Bestimung der Drehmomente um Stütze A oder Stütze B wird man eine Unbekannte (X oder Y) los

Drehmomente um Stütze A:

im Uhrzeigersinn =
$500\mathrm{N}\cdot 2\mathrm{m}=1000\mathrm{Nm}$

gegen den Uhrzeigersinn =
$Y\cdot 5\mathrm{m}$

Da die Drehmomente ausgeglichen sind:

$5Fm=1000\mathrm{Nm}$

Damit:

$Y=200\mathrm{N}$

Von hier aus gibt es zwei Methoden, um X zu bestimen. Entweder bestimmst du die Drehmomente um Stütze B und machst eine Berechnung wie oben. Oder du machst dir die Tatsache zunutze, dass X + Y der 500 N großen Kraft nach unten entsprechen muss.

Beide Methoden ergeben:

$X=300\mathrm{N}$

Fragen

1. Das Drehmoment (Drehwirkung) einer Kraft hängt von zwei Faktoren ab. Welche sind das?

Richtig ist:

• von der Kraft, die auf einen Drehpunkt wirkt
• von der Entfernung vom Drehpunkt zu dem Punkt, an dem die Kraft ansetzt

2. Was ist das Prinzip der Momente? Welche andere Regel gilt noch, wenn ein Objekt im Gleichgewicht ist?

Richtig ist:

1. Die Summe der Drehmomente um einen beliebigen Punkt im Uhrzeigersinn ist gleich der Summe der Drehmomente um diesen Punkt gegen den Uhrzeigersinn

3. Stell dir vor, unten versucht eine Person ein Brett ins Gleichgewicht zu bringen.

1. Berechne das Drehmoment der 4 N großen Kraft um o.
2. Berechne das Drehmoment der 6 N großen Kraft um o.
3. Wird sich das Brett ausgleichen? Wenn nicht, in welcher Weise wird es sich bewegen?
4. Welche zusätzliche Kraft wird am Punkt P benötigt, um das Brett auszubalancieren?
5. In welche Richtung muss diese Kraft wirken?

Richtig ist:

1. 16 Nm
2. 12 Nm
3. Nein, es wird sich im Uhrzeigersinn bewegen
4. 1 N
5. Nach unten

4. Betrachte das Diagramm B weiter oben.

1. Wie groß ist die Aufwärtskraft von der Stütze?
2. Wenn die Drehmomente um Punkt P bestimmt werden, welche Kräfte haben Drehmomente im Uhrzeigersinn? Was ist das Gesamtdrehmoment um P?
3. Welche Kraft oder Kräfte haben Drehmomente um P gegen den Uhrzeigersinn? Was ist das Gesamtdrehmoment um P gegen den Uhrzeigersinn?
4. Wenn du die Drehmomente um P vergleichst, gilt dann das Prinzip der Drehmomente?

Richtig ist:

1. 21 N
2. 10 N, 8 N, 3 N, 84 Nm
3. 21 N
4. 1 N
5. Ja, das Prinzip gilt