Kraft, Gewicht und Gravitation

Gravitationskraft

Wenn du ein Gewicht an einer Federwaage aufhängst, dann wird es von der Erde angezogen. Dieser Zug in Richtung Erdmittelpunkt wird als Gravitationskraft oder einfach Gravitation bezeichnet.

Auch Teilchenphysiker wissen bis heute nicht genau, was die Gravitation eigentlich verursacht, aber hier sind einige ihrer wichtigsten Merkmale:

Alle Massen ziehen sich gegenseitig an.
Je größer die Masse, desto stärker die Anziehungskraft.
Je näher sich die Massen sind, desto stärker die Anziehungskraft.

Die Gravitation zwischen kleinen Massen ist extrem schwach. Sie beträgt weniger als $\mathrm {10^{-7} \ N}$ zwischen dir und einer Katze auf deinem Schoß! Aber die Erde ist so massiv, dass ihr Gravitationszug stark genug ist, um die meisten Dinge fest auf dem Boden zu halten.

Gewicht

Gewicht ist ein anderer Name für die Gravitationskraft der Erde auf ein Objekt. Wie andere Kräfte auch, wird das Gewicht in Newton (N) angegeben.

In der Nähe der Erdoberfläche hat ein Objekt mit der Masse 1 kg ein Gewicht von etwa 9,81 N - das hängt aber vom Ort der Messung ab. Für viele alltägliche Berechnungen verwendet man meist 10 N, so auch auf dieser Homepage. Größere Massen haben größere Gewichte. Hier sind einige Beispiele:

Gravitationsfeldstärke, g

Die Erde hat ein Gravitationsfeld, das eine Kraft auf jede Masse in und auf ihr ausübt. In der Nähe der Erdoberfläche wirkt eine Gravitationskraft von 10 Newton auf jedes Kilogramm Masse: Die Gravitationsfeldstärke der Erde beträgt also 10 Newton pro Kilogramm ($\mathrm {\frac {N}{kg}}$).

Die Gravitationsfeldstärke wird durch das Symbol $g$ dargestellt.
Also: Gewicht = Masse $\cdot$ g

Schreibweise in Symbolen:

$W \ = \ m \ \cdot \ g$

Symbole und Einheiten:

$W$ = Gewicht in Newton ($\mathrm N$)
$m$ = Masse in Kilogramm ($\mathrm {kg}$)
$g$ = Gravitationsfeldstärke, $\mathrm {10 \ \frac {N}{kg}}$ in der Nähe der Erdoberfläche

In der alltäglichen Sprache verwenden wir oft das Wort "Gewicht", wenn es eigentlich "Masse" heißen sollte. Sogar Waagen, die eigentlich das Gewicht ermitteln, sind normalerweise in Masseneinheiten unterteilt. Aber die beiden Fallschirmspringer oben "wiegen" nicht 100 Kilogramm, sondern haben eine Masse von 100 Kilogramm und ein Gewicht von 1000 Newton.

Beispiel:

Wie groß die Beschleunigung der abgebildeten Rakete?

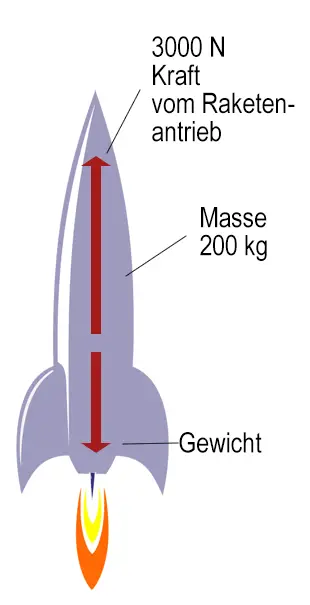
Um die Beschleunigung der Rakete zu bestimmen, musst du die resultierende Kraft kennen. Und um die herauszufinden, musst du wissen wieviel die Rakete wiegt.

Gewicht = $mg \ = \ \mathrm {200 \ kg \ \cdot \ 10 \ \frac {N}{kg} \ = 2000 \ N}$

Daraus folgt:

resultierende Kraft (nach oben) = $\mathrm {3000 \ N \ - \ 2000 \ N \ = \ 1000 \ N}$

Aber:

resultierende Kraft = Masse $\cdot$ Beschleunigung

Also:

$\mathrm {1000 \ N \ = \ 200 \ kg \ \cdot \ Beschleunigung}$

Die umgestellte Gleichung ergibt:

Beschleunigung der Rakete = $\mathrm {5 \ \frac {m}{s^2}}$

Veränderliches Gewicht, unveränderliche Masse

Auf dem Mond wäre dein Gewicht (in Newton) viel geringer als auf der Erde, weil das Gravitationsfeld des Mondes schwächer ist.

Auch auf der Erde kann dein Gewicht von Ort zu Ort leicht variieren, weil die Gravitationsfeldstärke der Erde nicht überall gleich ist. Wenn du dich von der Erde entfernst, nimmt dein Gewicht ab. Wenn du tief in den Weltraum fliegen würdest und du frei von jeglichem Gravitationszug wärst, wäre dein Gewicht null.

Ob auf der Erde, auf dem Mond oder tief im Weltraum, dein Körper hat immer den gleichen Widerstand gegen eine Bewegungsänderung. So ändert sich deine Masse ($\mathrm {kg}$) nicht - zumindest nicht unter normalen Umständen. Aber...

nach Einsteins Relativitätstheorie kann sich auch die Masse ändern. Zum Beispiel erhöht sie sich, wenn ein Objekt an Geschwindigkeit zulegt. Allerdings ist die Veränderung viel zu klein, um sich bei Geschwindigkeiten deutlich unter der Lichtgeschwindigkeit bemerkbar zu machen. Für alle praktischen Zwecke können wir also davon ausgehen, dass Masse konstant ist.

Zwei Bedeutungen für g

Die Beschleunigung eines jeden Objektes kann mit Hilfe der Gleichung Kraft = Masse x Beschleunigung bestimmt (Bild ganz oben). Zum Beispiel wirkt auf die Masse von 2 kg ein 20 N starke Kraft, also beträgt ihre Beschleunigung $\mathrm {10 \ \frac {m}{s^2}}$.

Das Ergebnis gilt auch für alle anderen Objekte auf dem Bild, auch für die beiden Fallschirmspringer. Die Beschleunigung liegt immer bei $\mathrm {10 \ \frac {m}{s^2}}$ oder $g$ (wobei $g$ die Gravitationsfeldstärke der Erde, $\mathrm {10 \ \frac {N}{kg}}$), ist.

Also hat das Symbol $g$ zwei Bedeutungen:

$g$ ist die Gravitationsfeldstärke ($\mathrm {10 \ \frac {N}{kg}}$).
$g$ ist die Beschleunigung im freien Fall ($\mathrm {10 \ \frac {m}{s^2}}$).

Ort	Masse	Gewicht
im Weltraum	100 kg	Null
auf dem Mond	100 kg	160 N
auf der Erde	100 kg	1000 N