Dehnen und Komprimieren
Plastisch und elastisch
Wenn du ein Lineal leicht biegst und es losläßt, springt es zurück in seine ursprüngliche Form. Materialien, die sich so verhalten, sind elastisch. Allerdings sind solche Materialien nicht mehr elastisch, wenn sie zu weit gebogen oder gestreckt werden. Sie brechen oder werden dauerhaft deformiert (aus der Form gebracht).
Kraft und Gewicht - Grundlegendes
- Eine Kraft wird in Newton (N) angegeben.
- Das Gewicht ist eine Kraft.
- Auf der Erde beträgt das Gewicht eines Objekts 10 N für jedes Kilogramm seiner Masse.
Wenn Plastilin gezogen oder gebogen wird, behält es seine neue Form. Materialien, die sich so verhalten, sind plastisch. (Materialien, die wir "Plastik" nennen, haben diesen Namen, weil sie plastisch und formbar sind, wenn sie heiß sind.)

Eine Feder dehnen
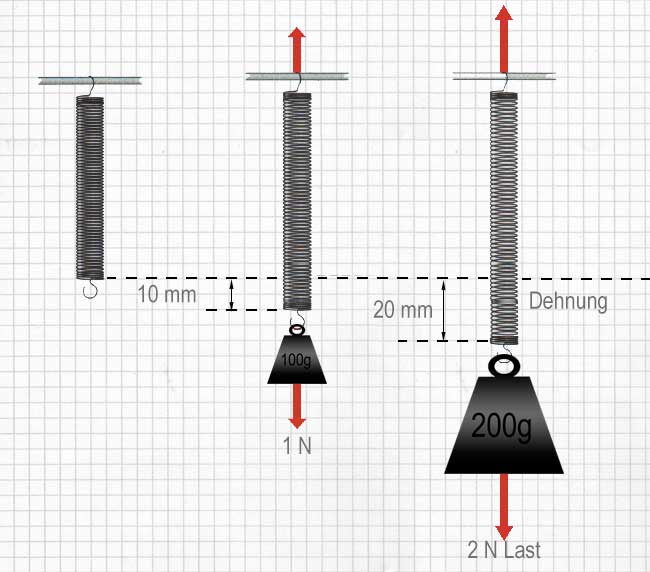
In dem folgenden Experiment wird eine Stahlfeder gestreckt, indem an eine Ende ein Gewicht gehängt wird. Die Kraft, die auf die Feder ausgeübt wird, nennt man Last. Weil g = 10 $\mathrm {\smash {\tfrac {N}{kg}}}$, beträgt die Last 1 N je 100 g Masse.
Wenn die Last erhöht wird, dehnt sich die Feder immer mehr. Ihre Ausdehnung ist der Unterschied zwischen der gestreckten und der ungestreckten Länge.
| Last | Dehnung |
|---|---|
| 0 | 0 |
| 1 | 10 |
| 2 | 20 |
| 3 | 30 |
| 4 | 40 |
| 5 | 58 |
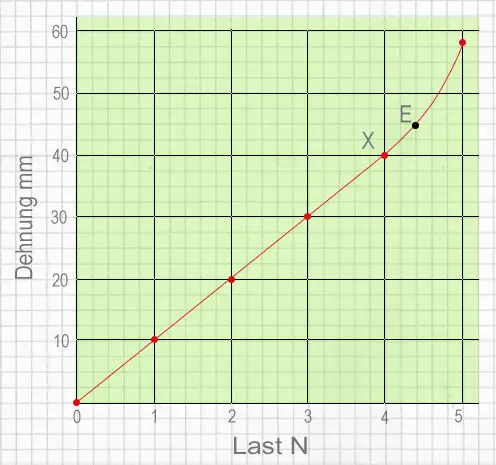
Die Wertepaare in der Tabelle können als Grafik dargestellt werden. Bis zu Punkt X hat die Linie folgende Merkmale:
- Die Linie ist gerade und geht durch den Ursprung.
- Wenn die Last verdoppelt wird, verdoppelt sich die Ausdehnung.
- Ausdehnung $\div$ Last ergibt immer den gleichen Wert (10 $\mathrm {\tfrac {mm}{N}}$).
- Jeder Anstieg der Last um 1 N erzeugt die gleiche Ausdehnung (10 mm).
Mathematisch können diese Merkmale wie folgt zusammengefasst werden:
Bis zu Punkt X verhält sich die Ausdehnung proportional zur Last.
Punkt E markiert eine weitere Veränderung im Verhalten der Feder. Bis zu diesem Punkt verhält sich die Feder elastisch und kehrt zu ihrer ursprünglichen Länge zurück, wenn die Last entfernt wird. E ist also die elastische Grenze der Feder. Jenseits von E bleibt die Feder dauerhaft gedehnt, auch wenn die Last entfernt wird.
Hookesches Gesetz
Im 17. Jahrhundert untersuchte Robert Hooke, wie Federn und Drähte sich dehnen, wenn Gewichte angehängt werden. Er stellte fest, dass bei vielen Materialien Ausdehnung und Belastung proportional zueinander sind, sofern die Elastizitätsgrenze nicht überschritten wird:
Ein Material gehorcht dem Hookeschen Gesetz, wenn unter seiner Elastizitätsgrenze seine Verlängerung proportional zur Last ist.
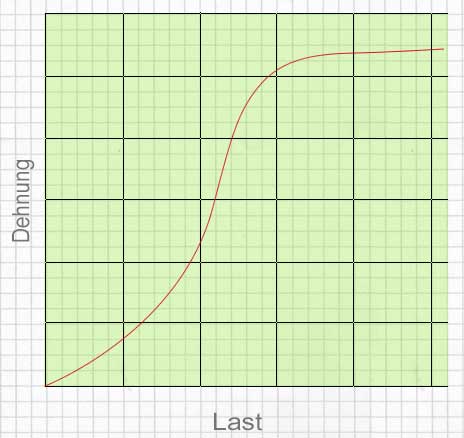
Stahldrähte dehnen sich nicht so weit wie Stahlfedern, aber auch sie gehorchen dem Hookeschen Gesetz genauso wie Glas und Holz, aber nicht Gummi.
Materialien können sowohl zusammengedrückt als auch gedehnt werden. Stahl ist fest, ob zusammengedrückt oder gedehnt (gespannt). Beton hält zwar einen großen Druck aus, aber keine große Spannung. So zerbricht er leicht, wenn er gedehnt oder gebogen wird. Um ihm eine größere Zug- (Streck-) Festigkeit zu verleihen, wird Beton mit Stahlstangen verstärkt.

Mehr über gedehnte Federn
In der graphischen Darstellung weiter oben erkennt man, dass Last $\div$ Dehnung immer den gleichen Wert ergibt, nämlich 0,1 $\mathrm {\smash{\tfrac {N}{mm}}}$, allerdings nur bis zu Punkt X. Dieser gleichbleibende Wert wird als Federkonstante bezeichnet:
Last = Federkonstante $\cdot$ Ausdehnung
Wenn du eine Feder dehnst (oder zusammendrückst), überträgst du Energie, die in der Feder gespeichert wird. Einige Spielzeugautos haben eine Feder, die man spannen kann. Wenn die Feder sich wieder entspannt, wird Energie freigesetzt und erzeugt Bewegung.
Die bis zu Punkt X gespeicherte Energie kann wie folgt berechnet werden:
Gespeicherte Energie (in Joule) = $\mathsf {\tfrac {1}{2} \cdot}$ Last (in N) $\cdot$ Ausdehnung (in m)
Fragen
Richtig ist:
Bis zu einem gewissen Punkt der Dehnung kehrt es immer wieder in seine Ausgangsform zurück
Richtig ist:
Dehnt man ein Material über seine Elastizitätsgrenze hinaus, kehrt es nicht wieder in seine Ausgangsform zurück
Richtig ist:
Nein
Die Last-Dehnungskurve für Gummi hat zu Beginn keinen Abschnitt mit einer geraden Linie. Somit verhält sich die Dehnung nicht proportional zur Last
- 40 mm
- Von 0 mm bis 88 mm
- 3,89 N
- 2,78 N
| Last (N) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Länge (mm) | 40 | 49 | 58 | 67 | 76 | 88 | 110 |
| Ausdehnung (mm) | 0 | 9 | 18 | 27 | 36 | 48 | 70 |