Der freie Fall (1)
Die Beschleunigung im freien Fall, g
Wenn du ein Bleigewicht und eine Feder fallen lässt, fallen zwar beide wegen der Schwerkraft nach unten, doch die Feder fällt wegen des Luftwiderstands viel langsamer.
Das Video oben zeigt, was passiert, wenn es keinen Luftwiderstand gibt. Beide Objekte fallen mit der gleichen Abwärtsbeschleunigung nach unten: 9,8 $\mathsf {\tfrac {m}{s^2}}$. Diese Größe nennt man Beschleunigung im freien Fall. Sie gilt für alle Objekte in der Nähe der Erdoberfläche, egal ob leicht oder schwer.
Die Beschleunigung im freien Fall wird mit dem Symbol $g$ dargestellt. Sein Wert variiert leicht von Ort zu Ort, weil auch die Erdanziehungskraft nicht überall gleich ist. Die Unterschiede machen jedoch weniger als 1% aus. Je weiter sich ein Objekt von der Erde weg in den Weltraum bewegt, umso mehr nimmt $g$ ab
Beachte, dass der Wert von $g$ in der Nähe der Erdoberfläche nahe bei 10 $\mathsf {\tfrac {m}{s^2} }$ liegt. Diese einfache Zahl ist für viele Berechnungen genau genug und wird auf dieser Homepage auch verwendet.

Bestimmung von $g$
Ein Experiment, wie man $g$ bestimmen kann, wird auf der linken Seite gezeigt. Im Prinzip wird die Zeit gemessen, wie lange die Kugel aus einer bekannten Höhe benötig, um zu Boden zu fallen, und um daraus die Beschleunigung zu berechnen. Der Luftwiderstand ist bei einer kleinen, schweren Kugel, die aus geringer Höhe fällt, sehr gering und hat wenig Einfluss auf die Beschleunigung der Kugel.

Die Kugel fällt, sobald der Strom für den Elektromagneten abgeschaltet wird. Der elektronische Timer schaltet sich automatisch ein, sobald die Kugel durch die obere Lichtschranke fällt, und wird automatisch abgeschaltet, sobald die Kugel die zweite Lichtschranke auf dem Boden erreicht hat. Ist die Fallhöhe $h$ und die Zeit $t$ bekannt, kann man mit dieser Gleichung $g$ berechnen:
${g \ = \ \frac {\Large {2h}}{\Large {t^2}}}$
Auf und ab
Im folgenden Beispiel sei $g$ 10 $\mathsf {\tfrac {m}{s^2}}$ und es gibt keinen Luftwiderstand.
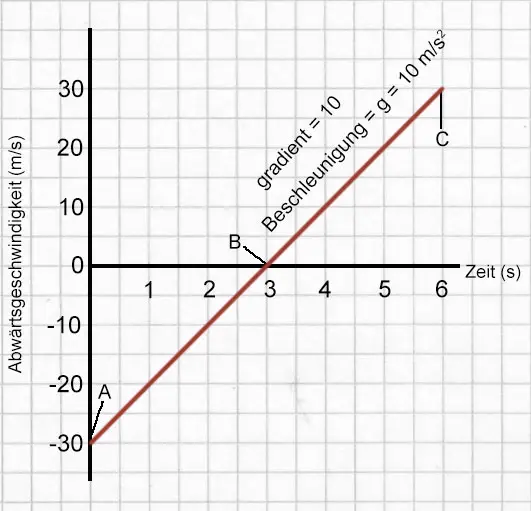
Die Billard-Kugel rechts wird mit einer Geschwindigkeit von 30 $\mathsf {\tfrac {m}{s}}$ nach oben geworfen. Das Diagramm unten zeigt die Geschwindigkeit der Kugel in jeder Sekunde während sie bis zum höchsten Punkt hochfliegt und dann in die Hand zurückfällt.
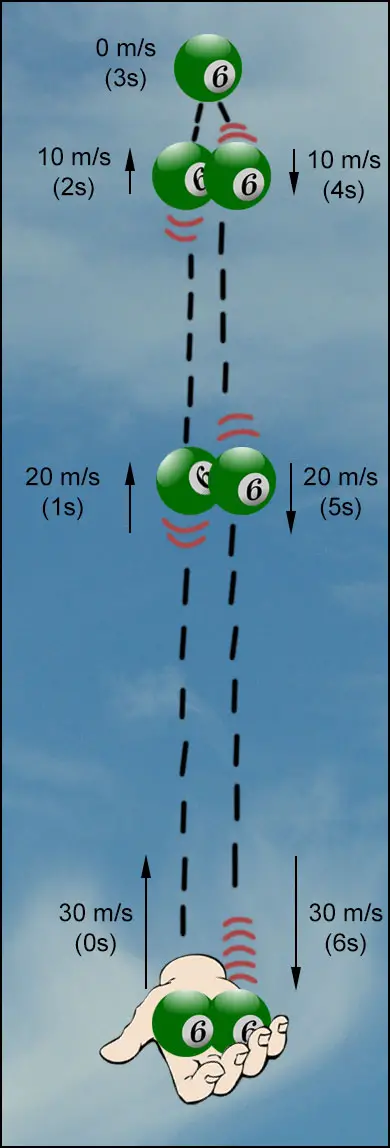
Da die Aufwärtsgeschwindigkeit mit 30 $\mathsf {\tfrac {m}{s}}$ genau so groß ist wie die Abwärtsgeschwindigkeit mit -30 $\mathsf {\tfrac {m}{s}}$, kann die Bewegung der Kugel wie folgt beschrieben werden:
| Bei 0 s . . . . | -30 $\mathsf {\tfrac {m}{s}}$ |
| Nach 1 s . . . . | -20 $\mathsf {\tfrac {m}{s}}$ |
| Nach 2 s . . . . | -10 $\mathsf {\tfrac {m}{s}}$ |
| Nach 3 s . . . . | 0 $\mathsf {\tfrac {m}{s}}$ |
| Nach 4 s . . . . | 10 $\mathsf {\tfrac {m}{s}}$ |
| Nach 5 s . . . . | 20 $\mathsf {\tfrac {m}{s}}$ |
| Nach 6 s . . . . | 30 $\mathsf {\tfrac {m}{s}}$ |
| Die Abwärtsgeschwindigkeit erhöht sich jede Sekunde um 10 $\mathsf {\tfrac {m}{s}}$ | |
Egal ob sich die Kugel nach oben oder unten bewegt, die Abwärtsgeschwindigkeit nimmt mit einer Geschwindigkeit von 10 $\mathsf {\tfrac {m}{s}}$ pro Sekunde zu. Also hat sie immer eine Abwärtsbeschleunigung von 10 $\mathsf {\tfrac {m}{s^2}}$, was unserem gesuchten $g$ entspricht. Auch wenn die Billard-Kugel nach oben fliegt oder an ihrem höchsten Punkt scheinbar still steht, erfährt sie immer noch eine Beschleunigung.
Unten siehst du ein Geschwindigkeits-Zeit-Diagramm für diese Bewegung.