Geschwindigkeit und Beschleunigung

Geschwindigkeit

Einige alltägliche Geschwindigkeiten im Vergleich:

Benötigte Zeit, um 1 km (1000 m) zurückzulegen
	Schnecke 330 h $\thickapprox$ 20.000 s
Sportler: 150 s	Formel 1 Auto: 10 s
Militär-Jet: 1,5 s	Space Shuttle: 0,1 s

Die durchschnittliche Geschwindigkeit eines Objekts berechnet man so:

$\mathrm {durchschnittliche \ Geschwindigkeit \ = \ \frac {\Large {zurückgelegter \ Weg}}{\Large Zeit}}$

Da der zurückgelegte Weg in Metern (m) und die dafür benötigte Zeit in Sekunden (s) gemessen wird, gibt man die Geschwindigkeit in Metern pro Sekunde $(\mathsf {\tfrac {m}{s}})$ an.

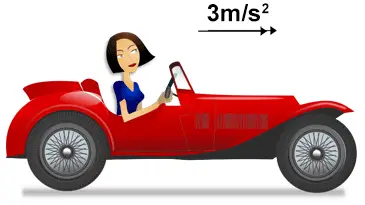
Zeit	Geschwindigkeit
0 s	0 $\mathrm {\tfrac {m}{s}}$
1 s	3 $\mathrm {\tfrac {m}{s}}$
2 s	6 $\mathrm {\tfrac {m}{s}}$
3 s	9 $\mathrm {\tfrac {m}{s}}$
4 s	12 $\mathrm {\tfrac {m}{s}}$

Zum Beispiel:
Wenn ein Auto 90 m in 3 s zurücklegt, dann fährt es mit einer durchschnittlichen Geschwindigkeit von:

$\mathrm {\large {\tfrac{90 m}{3 s}} = 30 \tfrac {m}{s}}$

Bei den allermeisten Autofahrten wird die Geschwindigkeit wohl variieren, so dass in der Regel die tatsächliche Geschwindigkeit zu jedem Zeitpunkt von der durchschnittlichen Geschwindigkeit abweicht. Um die tatsächliche Geschwindigkeit zu berechnen, musst du herausfinden, wie weit das Auto in der kürzesten Zeit fährt. Das kann man messen.

Zum Beispiel:
wenn sich ein Auto 0,20 Meter in 0,01 s fortbewegt gilt:

Geschwindigkeit = $\mathrm {\tfrac{\Large {0,20 \ m}}{\Large {0,01 \ s}} \ = \ 20 \ \tfrac {m}{s}}$

Manchmal muß man neben der Geschwindigkeit auch die Richtung angeben, in die sich ein Objekt bewegt. Beispielsweise könnte eine Durchsage der Polizei so lauten: "Der Einbrecher fährt mit 80 km/h nach Osten". Auf dem Papier kann die Fluchtrichtung und Geschwindigkeit des Bösewichts mit einem Pfeil dargestellt werden:

$\mathrm {\overrightarrow {\large {80 \frac {km}{h}}}}$

Eine physikalische Größe wie die Geschwindigkeit, die sowohl eine Richtung (z.B. nach rechts) als auch einen Betrag (z.B. 10 $\mathrm {\tfrac {m}{s}}$) hat, nennt man Vektor.

Beschleunigung

Ein Körper beschleunigt, wenn sich seine Geschwindigkeit ändert. Die Beschleunigung wird wie folgt berechnet:

$\mathsf {durchschnittliche \ Beschleunigung \ = \ \frac {Änderung \ der \ Geschwindigkeit}{Zeit}}$

Das Auto rechts oben beispielsweise beschleunigt von 0 auf 12 $\mathrm {\frac {m}{s}}$ in 4 s.

Also:

durchschnittliche Beschleunigung = $\mathrm { \frac {\Large {12 \frac {m}{s}}}{\Large {4 \ s}} \ = \ 3 \ \frac {m}{s^2}}$

Beachte, dass die Beschleunigung in Meter pro Sekunde² ($\mathrm {\tfrac {m}{s^2}}$) angegeben wird. Sie ist eine vektorielle, also gerichtete Größe. Dies zeigt man in der Regel mit einem Pfeil an. Auch kann man ein Plus-Zeichen (+) oder ein Minus-Zeichen (-) verwenden, um anzuzeigen ob sich die Geschwindigkeit erhöht oder verringert:

+ 3 $\mathrm {\tfrac {m}{s^2}}$ (Geschwindigkeit erhöht sich jede Sekunde um 3 $\mathrm {\tfrac {m}{s}}$)

- 3 $\mathrm {\tfrac {m}{s^2}}$(Geschwindigkeit verlangsamt sich jede Sekunde um 3 $\mathrm {\tfrac {m}{s}}$)

Eine negative Beschleunigung nennt man Verzögerung oder Verlangsamung. Eine gleichmäßige Beschleunigung bedeutet eine konstante (stetige) Beschleunigung.

Beispielrechnung

Das Auto unten fährt an Laterne A mit einer Geschwindigkeit von 12 $\mathrm {\tfrac {m}{s}}$ vorbei. Wie hoch ist seine Geschwindigkeit bei Laterne B nach 5 s, wenn seine Beschleunigung konstant 3 $\mathrm {\tfrac {m}{s^2}}$ beträgt?

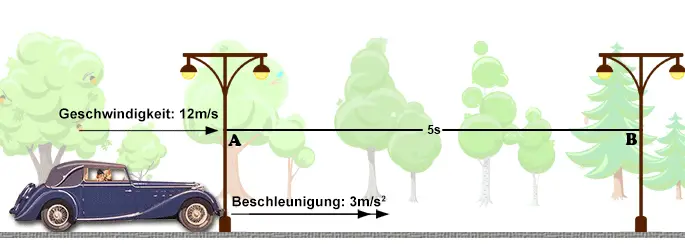
Die Geschwindigkeit des Autos nimmt jede Sekunde um 3 $\mathrm {\tfrac {m}{s}}$ zu. Nach 5 s Beschleunigung ist es also um 15 $\mathrm {\tfrac {m}{s}}$ schneller geworden. Die Geschwindigkeit bei Laterne B beträgt nun 27 $\mathrm {\tfrac {m}{s}}$.

So wird die Endgeschwindigkeit berechnet:

$\mathsf {\small {Endgeschwindigkeit \ = \ Anfangsgeschwindigkeit \ + \ extra \ Geschwindigkeit}}$

Also:

$\mathsf {\small {Endgeschwindigkeit \ = \ Anfangsgeschwindigkeit \ + \ (Beschleunigung \ \cdot \ Zeit)}}$

Die Gleichung gilt auch für eine Verlangsamung. Wenn das Auto bremst und sich um 3 $\mathrm {\tfrac {m}{s^2}}$ verlangsamt, hat es eine negative Beschleunigung: -3 $\mathrm {\tfrac {m}{s^2}}$.

1. Ein Auto fährt 600 m weit in 30 s.

1. Was ist seine durchschnittliche Geschwindigkeit?
2. Warum ist seine durchschnittliche Geschwindigkeit normalerweise immer anders als seine momentane, tatsächliche Geschwindigkeit?

Richtig ist:

1. 20 $\mathrm {\tfrac {m}{s}}$
2. Na klar, bei dem Verkehr in unseren Städten und Autobahnen muß ein Autofahrer immer entweder bremsen oder beschleunigen.

2. Ein Auto bewegt sich konstant mit 8 $\mathrm {\tfrac {m}{s}}$ fort

1. Welche Strecke legt das Auto in 8 s zurück?
2. Wie lang braucht das Auto um 160 m zurückzulegen?

Richtig ist:

1. 64 m
2. 20 s

3. Berechne die durchschnittliche Geschwindigkeit folgender Objekte für eine Strecke von 1 km:

a. Sportler benötigen dafür etwa 150 s	b. Ein Formel 1 Auto benötigt dafür etwa 10 s
c. Ein Militär-Jet benötigt dafür etwa 1,5 s	d. Das ehemalige Space Shuttle benötigte dafür etwa 0,1 s

Richtig ist:

1.     6,67 $\mathrm {\tfrac {m}{s}}$
2.      100 $\mathrm {\tfrac {m}{s}}$
3.      667 $\mathrm {\tfrac {m}{s}}$
4. 10.000 $\mathrm {\tfrac {m}{s}}$

4. Ein Auto hat eine Beschleunigung von $\mathrm {\overrightarrow {+2 \tfrac {m}{s^2}}}$

1. Was sagt das über die Geschwindigkeit und die Fahrtrichtung des Autos aus?
2. Was meint man mit einer Beschleunigung von -2 $\mathrm {\tfrac {m}{s^2}}$

Richtig ist:

1. Das Auto legt jede Sekunde 2 $\mathrm {\tfrac {m}{s}}$ an Geschwindigkeit zu
2. Das Auto bremst jede Sekunde um 2 $\mathrm {\tfrac {m}{s}}$ ab

5. Ein Auto benötigt 8 s um seine Geschwindigkeit von 10 $\mathrm {\tfrac {m}{s}}$ auf 30 $\mathrm {\tfrac {m}{s}}$ zu erhöhen.

Wie groß ist seine durchschnittliche Beschleunigung?

Richtig ist:

2,5 $\mathrm {\tfrac {m}{s^2}}$

6. Ein Motorrad, das mit 20 $\mathrm {\tfrac {m}{s}}$ fährt, braucht 5 s um zu stoppen. Wie groß ist seine durchschnittliche Verlangsamung?

Richtig ist:

4 $\mathrm {\tfrac {m}{s^2}}$

7. Ein Flugzeug hat beim Start eine konstante Beschleunigung von 3 $\mathrm {\tfrac {m}{s^2}}$.

1. Um wieviel schneller ist das Flugzeug nach 4 s?
2. Wenn das Flugzeug eine Leuchtmarkierung auf der Startbahn mit einer Geschwindigkeit von 20 $\mathrm {\tfrac {m}{s}}$ passiert, wie groß ist seine Geschwindigkeit 8 s später?

Richtig ist:

1. 12 $\mathrm {\tfrac {m}{s}}$
2. 44 $\mathrm {\tfrac {m}{s}}$

8. Ein Lkw fährt mit 25 $\mathrm {\tfrac {m}{s}}$. Nun bremst der Fahrer 4 s lang, was zu einer Verlangsamung des LKW um 2 $\mathrm {\tfrac {m}{s^2}}$ führt. Auf welche Geschwindigkeit fällt der LKW?

Richtig ist:

17 $\mathrm {\tfrac {m}{s}}$