Druck
Die Blöcke A und B ruhen auf einem weichen Untergrund. Beide wiegen das gleiche und üben die gleiche Kraft auf den Boden aus. Aber die Kraft, die von Block B ausgeht, ist über eine größere Fläche verteilt, die Kraftwirkung auf jeden einzelnen Quadratmeter reduziert wird. Der Druck unter Block B ist kleiner als der unter Block A.
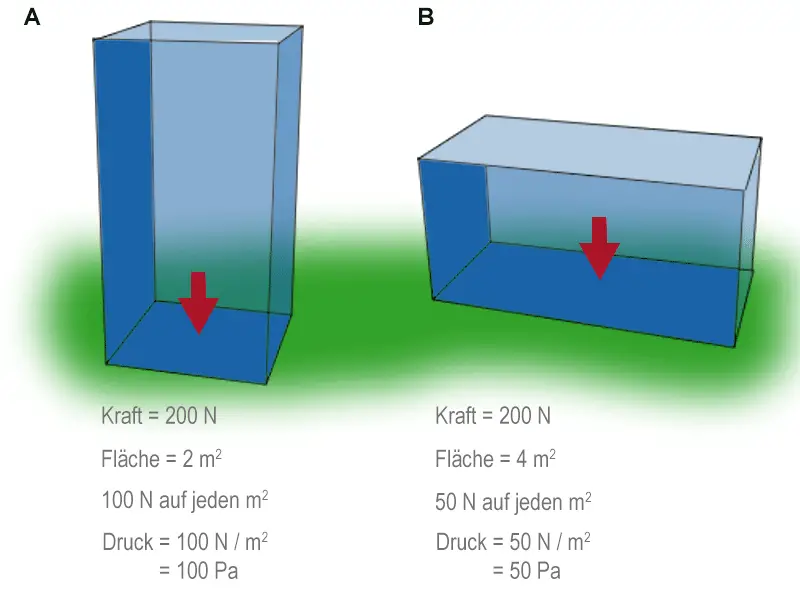
Für eine rechtwinklig zu einer Oberfläche wirkende Kraft wird der Druck wie folgt berechnet:
Druck = $\large {\mathsf {\tfrac {Kraft}{Fläche}}}$
In Symbolen:
$\mathrm p \ = \ \frac {F}{A}$
Wenn die Kraft in Newton (N) und die Fläche in Quadratmetern (m2) angegeben wird, so wird der Druck in Newton pro Quadratmeter ($\mathrm {\smash{\tfrac {N}{m^2}}}$) angegeben. 1 $\mathrm {\smash{\tfrac {N}{m^2}}}$ ist 1 Pascal (Pa).
| Wenn eine Kraft | über eine Fläche verteilt wird | beträgt der Druck |
| 100 N | 1 m2 | 100 Pa |
| 100 N | 2 m2 | 50 Pa |
| 100 N | 0,2 m2 | 500 Pa |
| 200 N | 0,2 m2 | 1000 Pa |
Für die meisten Druckmessungen ist das Pascal eine sehr kleine Einheit. In praktischen Situationen ist es oft bequemer, das Kilopascal (kPa) zu verwenden. 1 kPa = 1000 Pa.
| Erhöhung des Drucks durch Verkleinerung der Fläche | Verkleinerung des Drucks durch Erhöhung der Fläche |
|---|---|
 |
 |
| Die Bolzen auf einem Fußballstiefel haben nur einen kleinen Kontaktbereich mit dem Boden. Der Druck unter den Bolzen ist hoch genug, damit sie in den Boden sinken, was extra Griff gibt. | Skis haben eine große Fläche, um den Druck auf den Schnee zu reduzieren, damit sie nicht zu weit sinken. |
 |
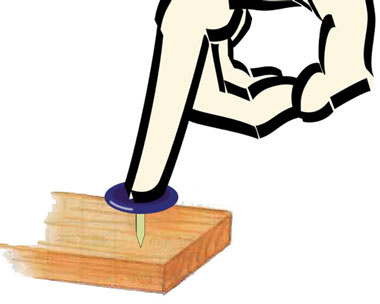 |
| Die Fläche unter dem Rand eines Messerblattes ist extrem klein. Darunter ist der Druck hoch genug, damit die Klinge leicht durch das Material schieben kann. | Unter dem winzigen Bereich der Spitze eines Ziehstiftes ist der Druck viel zu hoch für das Holz zu widerstehen. |
Typische Drücke

Rechenbeispiele
Beispiel 1
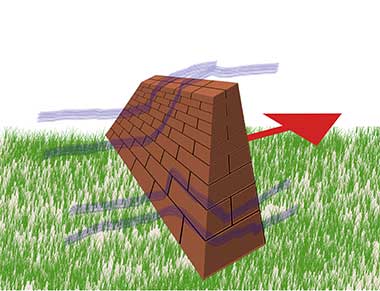
Der Winddruck auf die Mauer beträgt 100 Pa. Wenn die Mauer eine Fläche von 6 m2 hat, wie groß ist die Kraft, die auf sie wirkt?
Um dieses Problem zu lösen, musst du die Formel für den Druck umstellen:
$p \ = \ \frac {F}{A} \big | \cdot A$
$p \ \cdot \ A \ = \ F$
$\mathrm {100 \ Pa \ \cdot \ 6 \ m^2 \ = \ 600 \ N}$
Also beträgt die Kraft, die gegen die Mauer drückt, 600 N.
Beispiel 2
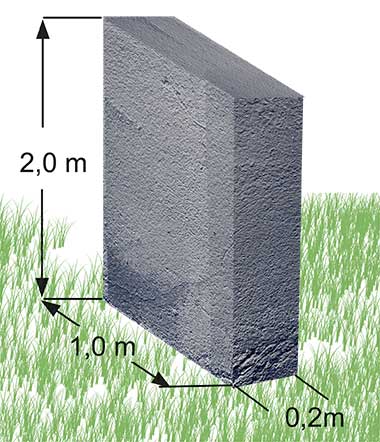
Ein Betonblock hat eine Masse von 2600 kg. Wenn der Block die Abmessung 0,2 m $\cdot$ 1,0 m $\cdot$ 2,0 m hat, was ist der maximale Druck, den er auf den Boden ausüben kann?
Weil g = 10 $\mathrm {\smash{\tfrac {N}{kg}}}$, hat der Betonblock mit einer Masse von 2600 kg ein Gewicht von 26.000 N, so dass die Kraft, die auf den Boden wirkt, auch 26.000 N ist.
Um den maximalen Druck auszuüben, muss der Block auf der Seite mit der kleinsten Fläche liegen. Diese Seite hat die Abmessung 1,0 m $\cdot$ 0,2 m und somit eine Fläche von 0,2 m2.
Damit:
Druck = $\large {\mathsf {\tfrac {Kraft}{Fläche}}}$
$\mathrm {p \ = \ \tfrac {26.000 \ N}{0,2 \ m^2} \ = \ 130.000 \ Pa}$
So beträgt der maximale Druck des Betonblocks auf den Boden 130.000 Pa oder 130 kPa.
Fragen
Richtig ist:
- 50 Pa
- 100 Pa
Richtig ist:
- 200 N
- 400 N
Richtig ist:
Die dicken Reifen des Traktors verteilen sein Gewicht auf eine größere Fläche
- 300 N
- 7500 Pa
- 500 Pa