Mehr über Vektoren

Vektoren und Skalare

Physikalische Größen, die sowohl eine Richtung als auch einen Betrag haben (wie eine Kraft), werden Vektoren genannt.

Zwei Kraftvektoren, die an einem Punkt wirken, können durch einen einzelnen Vektor mit demselben Effekt ersetzt werden. Man nennt diese Kraft kurz Resultierende oder Resultante. Untens kannst du sehen, wie man in zwei einfachen Fällen die Resultierende bestimmt. Die Suche nach der Resultierenden von zwei oder mehr Vektoren nennt man Addieren der Vektoren.

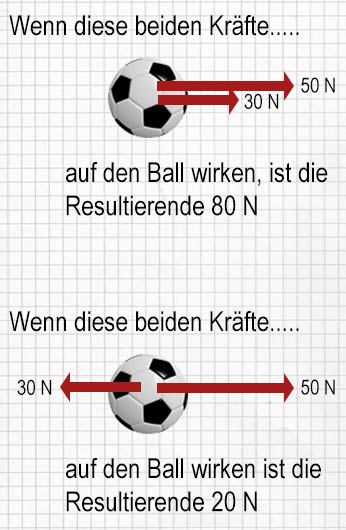
Physikalische Größen wie Masse und Volumen, die zwar einen Betrag, aber keine Richtung haben, werden Skalare genannt. Das Addieren von Skalaren ist einfach. Eine Masse von 30 kg, die zu einer Masse von 40 kg hinzugefügt wird, ergibt immer eine Masse von 70 kg.

Addieren von Vektoren: das Kräfteparallelogramm

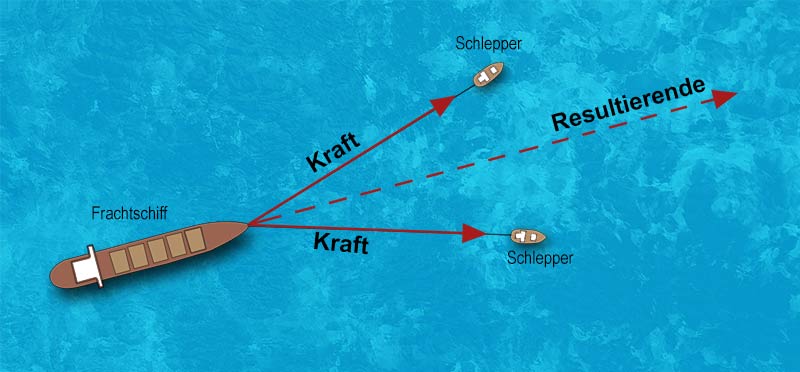
Das Kräfteparallelogramm ist eine geometrische Methode, um die Resultierende in Situationen wie oben zu bestimmen, wo die Vektoren nicht in einer Linie verlaufen. Dies funktioniert so:

Um die Resultiernde von zwei Vektoren zu bestimmen (z. B. Kräfte von 60 N und 80 N, die an einem Punkt O wirken, wie im Diagramm weiter unten):

Ziehe mit dem Lineal zwei rote Linien von Punkt O, um die Vektoren (Kräfte) darzustellen.
Ziehe zwei schwarze Linien, um ein Parallelogramm zu zeichnen.
Ziehe eine Diagonale von O und bestimme ihre Länge mit dem Lineal. Die Diagonale ist das Ergebnis sowohl in Größe als auch in Richtung.

Unten ist das Ergebnis: Die resultierende Kraft beider Kräfte ist 124 N.

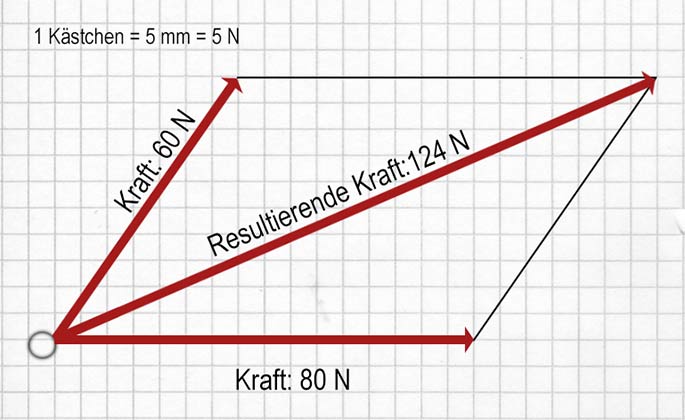
Du kannst die Diagonale auch berechnen:

Resultierende = $\mathrm {\sqrt{(a+x)^2 + h^2}}$

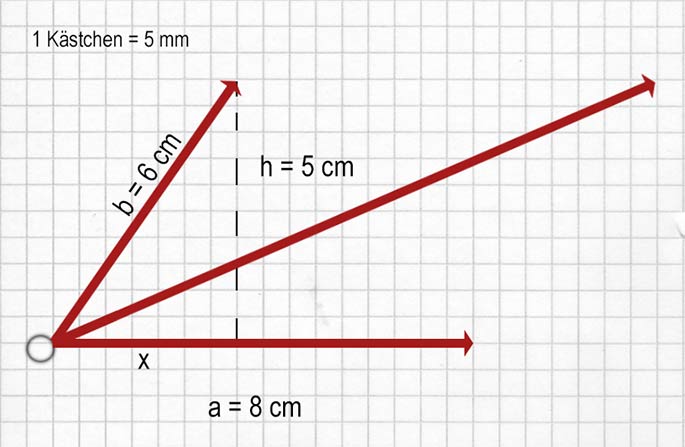
Wir nehmen den Satz des Pythagoras zu Hilfe und berechnen x:

$x^2 + h^2 = b^2 \ \big| \ - h^2$

$x^2 = b^2 - h^2$

$x^2 = \mathrm {(6 cm \cdot 6cm) - (5 cm \cdot 5cm) = 11 cm^2}$

$x = \mathrm {\sqrt {11cm^2} = 3,317 cm}$

Nun können wir nach obiger Gleichung die Länge der Diagonalen berechnen:

$\sqrt{(a+x)^2 + h^2} = \mathrm { \sqrt{(11,317 cm)^2} + 25 cm^2 = \sqrt{153,07 cm^2} = 12,37 cm}$

Oder man verwendet die Trigonometrie

Die horizontalen und vertikalen Komponenten einer Kraft F können auch mithilfe der Trigonometrie berechnet werden:

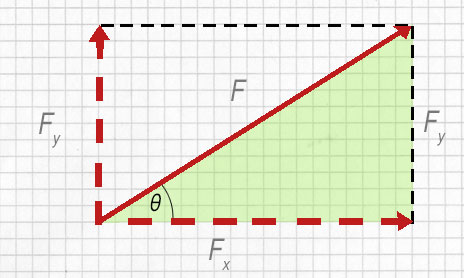
Im grünen Dreieck oben:

$\cos \ θ \ = \ \frac{F_x}{F}$

und

$\sin \ θ \ = \ \frac{F_y}{F}$

Also:

$F_x \ = \ F \cos \ θ$

und

$F_y \ = \ F \sin θ$

Die horizontalen und vertikalen Komponenten von F sind daher wie folgt:

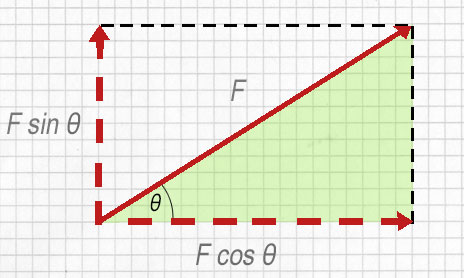
Komponenten eines Vektors

Die Parallelogramm-Methode funktioniert auch, wenn man eine einzelne Kraft durch zwei Kräfte ersetzen will. Wissenschaftlich gesehen ist es kein Problem, einen Vektor in zwei Komponenten zu zerlegen. Wenn man ein Kräfteparallelogramm verwendet, so beschreibt die Diagonale den Vektor, den man in zwei Komponenten zerlegen will.

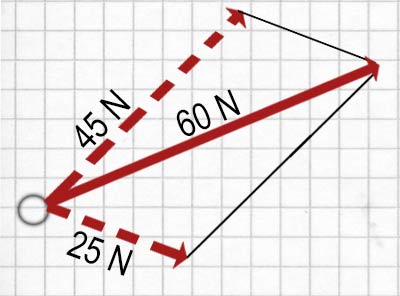
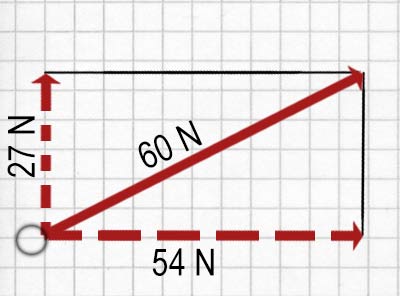
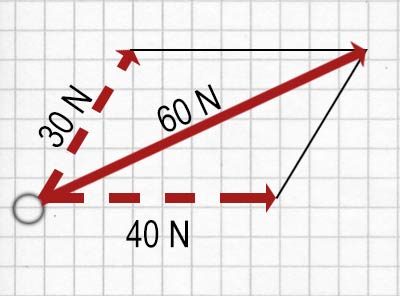
Oben siehst du einige der Möglichkeiten, wie eine Kraft von 60 N in zwei Komponenten zerlegt werden kann. Es gibt noch endlose andere Möglichkeiten.

Komponenten im rechten Winkel

Bei der Ausarbeitung der Auswirkungen einer Kraft hilft es manchmal, die Kraft in Komponenten rechtwinklig zu zerlegen. Wenn ein Hubschrauber beispielsweise seinen Hauptrotor kippt, hat die Kraft vertikale und horizontale Komponenten, die den Hubschrauber heben und ihn nach vorne bewegen.

Fragen

Antworten können aufgeklappt werden