Dichte und Volumen
Volumen
Den Raum, den ein Objekt einnimmt, nennt man Volumen.
Die Basiseinheit des Volumens ist der Kubikmeter (m3). Allerdings ist 1 Kubikmeter für die alltägliche Arbeit der Physiker ein ziemlich großes Volumen, so dass oft kleinere und bequemere Einheiten verwendet werden, wie in den folgenden Abbildungen dargestellt:
| Kubikmeter (m3) | Liter (l) | Kubikzentimeter oder Milliliter (cm3 oder ml) |
|---|---|---|
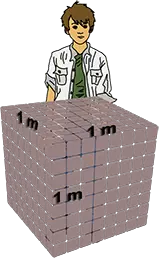
| 1 Kubikmeter (m3) ist das Volumen eines Würfels mit 1 m Kantenlänge | 1 Liter entspricht dem Volumen von 1 Kubikdezimeter (dm3) | 1 Kubikzentimeter entspricht dem Volumen eines Würfels mit 1 cm Kantenlänge |
 |

|

|
| 1 Kubikmeter (m3) = 1000 Liter (l) | 1 Liter (l) = 1000 Kubikzentimeter (cm3) = 1000 Milliliter (ml) | 1 Kubikzentimeter = 1 Milliliter |
Dichte
Ist Blei schwerer als Wasser? Nicht unbedingt! Es hängt davon ab, wie die Blei- und Wassermengen miteinander verglichen werden. Denn Blei hat eine höhere Dichte als Wasser und so sind In jedem Kubikmeter Blei mehr Kilogramm als in einem Kubikmeter Wasser "verpackt".

Die Dichte eines Materials wird so berechnet:
$\mathrm {Dichte \ = \ \frac {\Large Masse}{\Large Volumen}}$
Im Falle des Wassers bedeutet dies folgendes:
- 1000 kg Wasser nimmt ein Volumen von 1 m3 ein,
- 2000 kg Wasser haben ein Volumen von 2 m3,
- 3000 kg Wasser haben ein Volumen von 3 m3 usw.
Wenn man sich diese Werte anschaut, kann man leicht erkennen, dass die Dichte von Wasser 1000 kg / m3 beträgt.
Wenn die Masse in Gramm (g) und das Volumnen in Kubikzentimeter (cm3) gemessen werden, ist es einfacher, die Dichte in g / cm³ zu anzugeben. Die Umrechnung in kg / m3 ist einfach:
$\mathrm {1 \ g/cm^{3} \ = \ 1000 \ kg/m^{3}}$
Die Dichte des Wassers beträgt 1 g/cm3. Dieser so einfach erscheinende Wert ist kein Zufall. Das Kilogramm (1000 g) wurde ursprünglich als die Masse von 1000 cm3 Wasser (rein und bei 4 °C) definiert. Allerdings haben sich bei den frühen Messungen kleine Fehler eingeschlichen, so dass dies nicht mehr als Definition des Kilogramms verwendet wird.
| Stoff | Dichte kg / m3 |
Dichte g / cm3 |
Stoff | Dichte kg / m3 |
Dichte g / cm3 |
|---|---|---|---|---|---|
| Luft | 1,3 | 0,0013 | Granit | 2700 | 2,7 |
| Expandiertes Polystyrol | 14 | 0,014 | Aluminium | 2700 | 2,7 |
| Holz der Buche | 750 | 0,75 | rostfreier Stahl | 7800 | 7,8 |
| Benzin | 800 | 0,80 | Kupfer | 8900 | 8,9 |
| Eis (0 °C) | 920 | 0,92 | Blei | 11.400 | 11,4 |
| Polyethylen | 950 | 0,95 | Quecksilber | 13.600 | 13,6 |
| Wasser (4 °C) | 1000 | 1,0 | Gold | 19.300 | 19,3 |
| Beton | 2400 | 2,4 | Platin | 21.500 | 21,5 |
| Glas (variiert) | 2500 | 2,5 | Osmium | 22.600 | 22,6 |
Die Dichte berechnen
Die Gleichung, welche Dichte, Masse und Volumen verbindet, kann mit Symbolen dargestellt werden:
$\rho \ = \ \frac {\Large m}{\Large V}$
$\rho$ = Dichte, m = Masse und V = Volumen
Diese Formel kann man umstellen:
$\mathrm {V \ = \ \frac {\Large m}{\Large \rho}}$
und
$\mathrm {m \ = \ V \ \cdot \ \rho} $
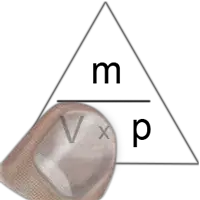
Dies ist nützlich, wenn zwar die Dichte bekannt ist, aber das Volumen oder die Masse berechnet werden soll. Auf der rechten Seite ist eine Methode, wie man alle drei Gleichungen findet. Beispiel:
Nimm die Tabelle oben zu Hilfe und berechne die Masse von Stahl, wenn er das gleiche Volumen einnimmt wie 5400 kg Aluminium.
Zuerst berechnet man das Volumen 5400 kg Aluminium. Dichte von Aluminium laut Tabelle: 2700 kg/m3, die Masse ist bekannt: 5400 kg, und das Volumen soll berechnet werden. Damit:
$ \mathrm {V \ = \ \frac {\Large m}{\Large \rho} \ = \ \mathrm {\frac {\Large {5400 \ kg}}{\Large {2700 \ kg/m^3}} \ = \ 2 \ m^3}} $
Wir wollen also wissen, wieviel Masse haben 2 m3 Stahl? Dichte von Stahl laut Tabelle: 7800 kg/m3, das Volumen ist bekannt: 2 m3, und die Masse soll berechnet werden. Damit:
$m \ = \ V \rho \ = \ \mathrm {7800 \ kg/m^3 \ \cdot \ 2 \ m^3 \ = \ 15.600 \ kg} $
Die Masse von 2 m3 Stahl beträgt also 15.600 kg!
Fragen
Antworten können aufgeklappt werden
| a) Liter | b) cm3 | c) ml |
| a) 200 l | b) 2 x 105 cm3 | c) 2 x 105 ml |
| a) Wieviel ist das in g/cm3 ? | b) Wieviel Masse haben 20 cm3 Aluminium ? |
| c) Welches Volumen hat eine Masse von 27 g Aluminium ? | |
| a) 2,7 g/cm3 | b) 54 g | c) 10 cm3 |
Nimm die Dichte-Tabelle weiter oben zu Hilfe und beantworte folgende Fragen: