Berechnung von potentieller und kinetischer Energie
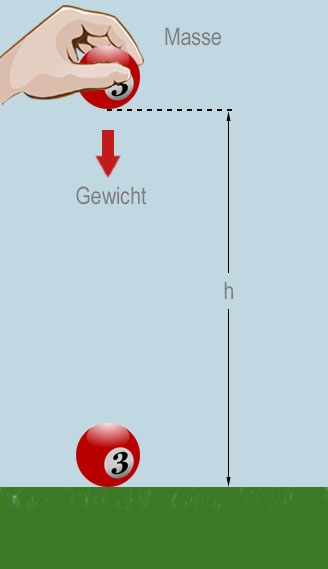
Die Kugel unten hat wegen der Gravitationskraft der Erde und ihrer Position über dem Boden potentielle Energie. Wenn die Kugel fällt, erhält sie kinetische Energie. Sowohl potentielle Energie als auch kinetische Energie können berechnet werden.
Berechnung der potentiellen Energie
Die potentielle Energie der Kugel ist gleich der Arbeit, die verrichtet würde, wenn sie zu Boden fällt. Unter der Annahme, dass es keinen Luftwiderstand gibt, ist die potentielle Energie ebenfalls gleich der Arbeit, die beim Anheben der Kugel um den Weg h vom Boden verrichtet würde:
Gewichtskraft der Kugel = $m \cdot g$
Also:
Benötigte Kraft zum Anheben der Kugel = $m \cdot g$
Also:
verrichtete Arbeit beim Anheben der Kugel = Kraft $\cdot$ Weg = $m \cdot g \cdot h$
Für ein Objekt der Masse m in einer vertikalen Höhe h über dem Boden gilt also:
Potentielle Energie = $\scriptsize m \cdot g \cdot h$
Beispiel:
Wenn sich eine Masse von 2 kg in 3 m Höhe über dem Boden befindet und g = 10 $\mathsf {\smash {\frac{N}{kg}}}$ ist die potentielle Energie:
2 kg $\cdot$ 3 m $\cdot$ 10 $\mathsf {\smash {\frac{N}{kg}}}$ = 60 J
Berechnung der kinetischen Energie

Die kinetische Energie der Kugel ist gleich der Arbeit, die sie bei der Beschleunigung von $null$ auf $v$ verrichtet:
$\mathsf {Arbeit} \ (W) =$
| $= \mathsf {Kraft} \ (F)$ | $\cdot \ \mathsf {Weg} \ (s)$ | ||
| $= \mathsf {Masse} \ (m)$ | $\cdot \ \mathsf {Beschleunigung} \ (a)$ | $\cdot \ \mathsf {Weg} \ (s)$ | |
| $= \mathsf {Masse} \ (m)$ | $\require{cancel} \cdot \ \frac{\large {\mathsf {Änderung \ der \ Geschwindigkeit}}}{\large {\mathsf {\cancel{Zeit}}}}$ | $\cdot \ \mathsf {Geschwindigkeit}$ | $\require{cancel} \cdot \ \mathsf {\cancel{Zeit}}$ |
| $= \mathsf {Masse} \ (m)$ | $\cdot \ \mathsf {Änderung \ der \ Geschwindigkeit}$ | $\cdot \ \mathsf {Geschwindigkeit}$ | |
| $= \ m$ | $\cdot \ v$ | $\cdot \ \frac{1}{2} v$ | |
| $= \ \frac{1}{2} mv^2$ |
Wird ein Körper der Masse $m$ aus der Ruhe heraus auf die Geschwindigkeit $v$ beschleunigt, so muss man dafür die Beschleunigungsarbeit $W$ verrichten. Bei konstanter Kraft gilt:
$W = Fs$
Die Kraft erteilt dem Körper eine gleichmäßige Beschleunigung $a$, nach der Grundgleichung der Mechanik ist $F=ma$. Nach einer Zeit $t$ ist die Geschwindigkeit $v=at$ und es wurde der Weg $s= \tfrac 1 2 a t^2$ zurückgelegt.
Alles oben eingesetzt ergibt die Beschleunigungsarbeit:
$W = m a \cdot \frac 1 2 \ a t^2 = \frac 1 2 \ m v^2$
Da die kinetische Energie in Ruhe den Wert Null hat, erreicht sie nach dem Beschleunigungsvorgang genau diesen Wert $W$. Folglich gilt für einen Körper der Masse $m$ mit der Geschwindigkeit $v$:
$\mathrm {Kinetische \ Energie} \ (E_\mathrm{kin}) \ = \ \frac{1}{2} mv^2$
Skalare Energie
Energie ist eine skalare Größe: sie hat einen Betrag, aber keine Richtung. Du musst also bei der Berechnung von Energie keine Richtung berücksichtigen.
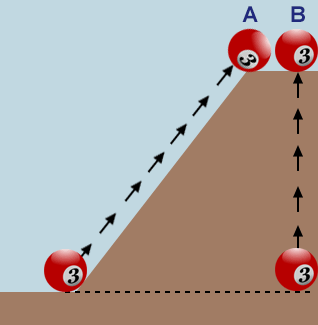
Die Kugeln A und B haben die gleiche Masse und befinden sich auf gleicher Höhe über dem Boden. Kugel B wurde vertikal angehoben, Kugel A wurde eine glatte Steigung hinauf gerollt. Obwohl Kugel A weiter bewegt werden musste, wurde weniger Kraft benötigt, um sie zu bewegen, und die Arbeit war die gleiche, die bei Kugel B verrichtet wurde. Beide Kuglen haben daher die gleiche potentielle Energie.
Die potentielle Energie (mgh) hängt von der vertikalen Zunahme der Höhe h ab und nicht von einem bestimmten Weg, der zum Erreichen dieser Höhe zurückgelegt wird.
Probleme mit der potentiellen und kinetischen Energie
Beispiel:
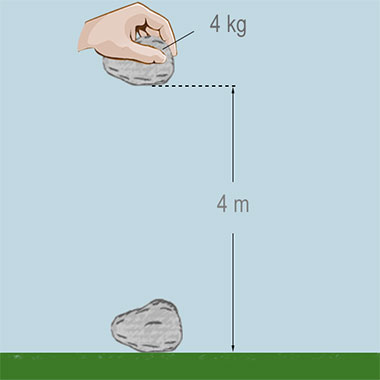
Wie groß ist die kinetische Energie des Steins, wenn er bis zur Hälfte des Weges zum Boden gefallen ist? (g = 10 $\mathrm {\smash {\frac{N}{kg}}}$)
Bei Problemen wie diesem musst du zur Berechnung nicht unbedingt die Gleichung
$\smash {E_\mathrm{kin} \ = \ \frac{1}{2} mv^2}$
verwenden.
Wenn der Stein fällt, ist die Zunahme seiner kinetischen Energie gleich dem Verlust seiner potentiellen Energie.
Also kannst du stattdessen so vorgehen:
Höhenverlust des Steins = 2 m
Also:
Verlust von potentieller Energie = $m \cdot g \cdot \ h \ = \ \mathrm {4 kg \ \cdot 10 \frac{N}{kg} \ \cdot \ 2 m \ = \ 80 \ J}$
Also:
Zunahme an kinetischer Energie = 80 J
Da der Stein zu Beginn keine kinetische Energie hatte, ist 80 J die kinetische Energie des Steines auf halbem Weg.
Beispiel:
Der Stein rutscht einen kleinen Abhang hinunter. Welche Geschwindigkeit hat er, wenn er den Boden erreicht? (g = 10 $\mathrm {\smash {\frac{N}{kg}}}$)
Diese Aufgabe kann ebenfalls unter Berücksichtigung der Änderungen der Energie gelöst werden.
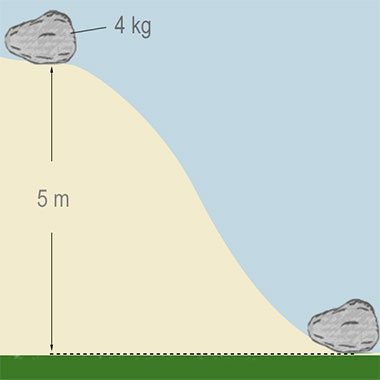
Oben am Hang hat der Stein eine zusätzliche potentielle Energie.
Wenn er den Boden erreicht, wurde all die potentielle Energie in kinetische Energie umgewandelt.
potentielle Energie am oberen Ende der Steigung:
$m \cdot g \cdot \ h \ = \ \mathrm {4 kg \ \cdot 10 \frac{N}{kg} \ \cdot \ 5 m \ = \ 200 \ J}$
Also:
kinetische Energie am unteren Ende der Steigung = 200 J
Also:
$\frac{1}{2} mv^2 \ = \ 200 \ \mathrm J$
Dies ergibt:
$v \ = \ \mathrm {10 \frac{m}{s}}$
Die Geschwindigkeit des Steins am unteren Ende der Steigung beträgt also $\mathrm {10 \frac{m}{s}}$.
Anmerkung: Wenn der Stein senkrecht fällt, würde er mit der gleichen potentiellen Energie beginnen und mit der gleichen kinetischen Energie enden, so dass seine Endgeschwindigkeit immer noch $\mathrm {10\frac{m}{s}}$ betragen würde.
Fragen
Angenommen g ist $\mathrm {10 \frac{N}{kg}}$ und der Luftwiderstand und andere Reibungskräfte sind vernachlässigbar.
Richtig ist:
- 240 J
- 360 J
Richtig ist:
- 75 J
- 300 J
Richtig ist:
$\mathrm {20 \frac{m}{s}}$
Richtig ist:
- 25 J
- 25 J
- 5 m
- 5 m