Bewegungsgleichungen
Verschiebung
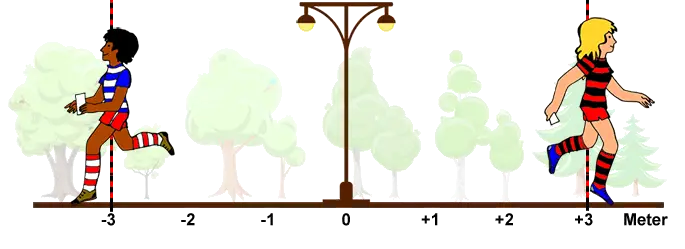
Wenn sich ein Objekt in eine bestimmte Richtung bewegt, so nennt man den zurückgelegten Weg von einer Stelle zur anderen Stelle Verschiebung. Dabei handelt es sich um einen Vektor. In einfachen Fällen kann die Vektorrichtung mit einem Plus-Zeichen (+) oder einem Minus-Zeichen (-) angezeigt werden. Oben zum Beispiel ist die eine Person von der Laterne um -3 m verschoben, die andere Person ist um +3 m (oft ohne das + Zeichen dargestellt) von der Laterne verschoben.
Gleichungen, die s, u, v, a und t in Zusammenhang bringen
u = Anfangsgeschwindigkeit ($\mathsf {\tfrac {m}{s}}$)
v = Endgeschwindigkeit ($\mathsf {\tfrac {m}{s}}$)
a = Beschleunigung ($\mathsf {\tfrac {m}{s^2}}$)
t = Zeit (s)
Bitte s, die Verschiebung in Meter, nicht mit dem Symbol für Sekunde (ebenfalls s) verwechseln
Viele Probleme mit bewegten Objekten können mit nur vier Gleichungen gelöst werden. Sie gelten aber nur, wenn die Bewegung in einer geraden Linie verläuft und die Beschleunigung gleichmäßig (konstant) ist.
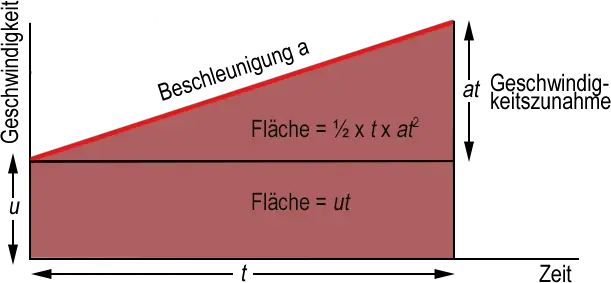
In den Gleichungen werden fünf Symbole verwendet. Das Diagramm auf der linken Seite zeigt, was sie bedeuten: Das Auto hat eine Beschleunigung a. Es passiert den ersten Marker (A) mit der Geschwindigkeit u, (seiner Anfangsgeschwindigkeit). t Sekunden später passiert es den zweiten Marker (B) mit der Geschwindigkeit v (seiner Endgeschwindigkeit). Es hat sich dann um den Wert s verschoben.
Hier sind die Gleichungen. Jede verbindet vier der fünf Größen:
| ${v \ = \ u \ + at}$ | ohne s |
| ${s \ = \ ut \ + \ \frac {l}{2}at^2}$ | ohne v |
| ${s \ = \ \frac {l}{2}(u \ + \ v)t}$ | ohne a |
| ${v^2 \ = \ u^2 \ + \ 2as}$ | ohne t |
Wenn die Werte von drei dieser Größen bekannt sind, kannst du den Wert der vierten Größe mit der entsprechenden Gleichung berechnen.
Ein Auto beschleunigt auf einer geraden Straße aus dem Stillstand mit 3 $\mathrm {\tfrac {m}{s^2}}$. Wie weit ist das Auto nach 4 s gefahren?
In diesem Fall ist:
- s der zu bestimmende Wert (Verschiebung)
- u ist null, weil das Auto aus dem Stillstand anfährt
- a ist 3 $\mathsf {\tfrac {m}{s^2}}$
- t ist 4 s
Die Gleichung, die s, u, a und t, aber nicht v enthält, lautet:
$s \ = \ ut \ + \ \frac {l}{2}at^2 \ = \ \mathrm {(0 \ \cdot \ 4) \ + \ (\frac {l}{2} \ \cdot \ 3 \ \cdot \ 4^2) = 24 \ m}$
Negative und positive Verschiebung
u, v, a und s sind Vektoren, also musst du die Richtung berücksichtigen, wenn du in die Gleichungen Zahlen einsetzt. Grundsätzlich geht man davon aus, dass alle vier Vektoren in die gleiche Richtung zeigen (z. B. nach rechts). Wenn also irgendwelche Vektoren in die entgegengesetzte Richtung zeigen, musst du sie als negativ (-) bezeichnen.
Eine Verlangsamung ist beispielsweise eine negative Beschleunigung. Mathematisch gesehen ist eine negative Beschleunigung eine Beschleunigung in die entgegengesetzte Richtung.
Beispiel:
Das Auto (Bild unten) fährt mit 20 $\mathrm {\tfrac {m}{s}}$ entlang einer geraden Straße. Der Fahrer tritt für 5 s auf die Bremse. Wenn der Bremsvorgang eine Verlangsamung des Autos von 3 $\mathrm {\tfrac {m}{s^2}}$ zur Folge hat, wie hoch ist die Endgeschwindigkeit des Autos?
In diesem Fall:
- u ist 20 $\mathsf {\tfrac {m}{s}}$ (positiv, weil sich das Auto nach rechts bewegt)
- v ist die gesuchte Endgeschwindigkeit
- a ist -3 $\mathsf {\tfrac {m}{s^2}}$ (negativ, weil es eine Verlangsamung ist)
- t ist 5 s
Die Gleichung, die u, v, a und t enthält, aber nicht s, lautet
$v \ = \ u \ + \ at \ = \ \mathrm {20 \ + \ (-3 \ \cdot \ 5) \ = \ 20 \ - \ 15 \ = \ 5 \frac {m}{s}}$
Folglich: Endgeschwindigkeit = 5 $\mathsf {\tfrac {m}{s}}$ (Das Auto fährt nach rechts, weil das Ergebnis positiv ist)
Erklärung der Gleichungen
| ${v \ = \ u \ + \ at}$ | ${s \ = \ ut \ + \ \frac {1}{2}at^2}$ |
| $\mathrm {at}$ (Beschleunigung x Zeit) ist die Zunahme der Geschwindigkeit. Diese Gleichung sagt also folgendes aus: Endgeschwindigkeit = Anfangsgeschwindigkeit + Geschwindigkeitszunahme |
Diese Gleichung findet man, indem man die Fläche unter einem Geschwindigkeit-Zeit-Diagramm für ein Objekt ausrechnet, das von einer Geschwindigkeit zur anderen beschleunigt. Die Fläche gibt die zurückgelegte Strecke und damit die Verschiebung wider. |
| $\mathrm {s \ = \ \frac {1}{2}(u \ + \ v)t}$ |
 |
| $\mathrm {\frac {1}{2}(u \ + \ v)}$ ist die durchnittliche Geschwindigkeit. Diese Gleichung sagt also folgendes aus: Zurückgelegter Weg = Durchschnittsgeschwindigkeit x benötigte Zeit |
|
| $\mathrm {v^2 \ = \ u^2 \ + \ 2as}$ | |
| Diese Gleichung findet man durch die Kombination der beiden Gleichungen oben unter Eliminierung von t |