Der freie Fall (2)
Bestimmen von $g$
| $v \ = \ u \ + \ at$ | s = Verschiebung u = Anfangsgeschwindigkeit v = Endgeschwindigkeit t = Zeit a = Beschleunigung (g) |
| $s \ = \ ut \ + \ \frac {1}{2} \ at^2 $ | |
| $s \ = \ \frac {1}{2}(u \ + \ v)t)$ | |
| $v^2 \ = \ u^2 \ + \ 2as$ | |
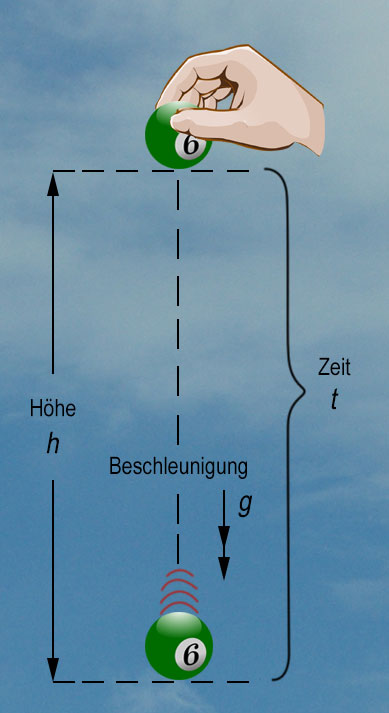
Die zweite Gleichung oben kann man zur Bestimmung von $g$ verwenden, sobald man die Zeit gemessen hat, die ein Objekt benötigt, um aus einer Höhe $h$ auf den Boden zu fallen (siehe unten links). In diesem Fall ist $a \ = \ g$, $s \ = \ h$ und $u \ = \ 0$, weil die Billard-Kugel aus dem Ruhezustand herabfällt.
Mit dieser Gleichung kann $g$ aus den Messungen von $h$ und $t$ berechnet werden (siehe vorherige Freier Fall - 1).
Aufgaben lösen
Beispiel:
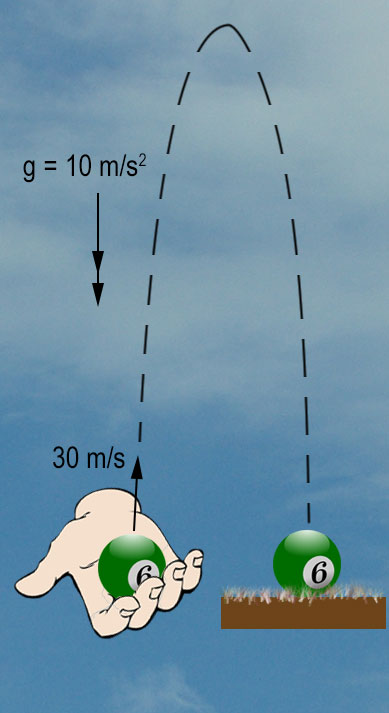
Auf dem Bild oben rechts wird eine Billard-Kugel aus Bodennähe mit einer Geschwindigkeit von 30 $\mathsf {\tfrac {m}{s}}$ in die Höhe geworfen. Nach wieviel Sekunden wird sie wieder auf den Boden aufschlagen? (Wir nehmen an, dass g = 10 $\mathrm {\tfrac {m}{s^2}}$ und dass der Luftwiderstand vernachlässigbar ist.)
Bei der Verwendung der Gleichungen der Bewegung, um solche Probleme zu lösen, findest Du diese Tipps vielleicht hilfreich:
- Verwende ein Plus (+) - Zeichen, um die Abwärtsrichtung anzuzeigen. Bei der Problemstellung oben ist die Anfangsgeschwindigkeit der Kugel nach oben also $u \ = \ \mathrm {-30 \ \tfrac {m}{s}}$. Die Kugel beschleunigt nach unten, also $a \ = \ g \ = \ \mathrm {+10 \ \tfrac {m}{s^2}}$.
- Denke daran, dass $s$ für die Verschiebung vom Ausgangspunkt steht, und nicht für die zurückgelegte Gesamtstrecke. Die Kugel legt eine Strecke von vielen Metern zurück, aber wenn sie zum Ausgangspunkt zurückkehrt, ist seine vertikale Verschiebung 0.
- Achte auf nützliche "versteckte" Informationen. Wenn zum Beispiel ein Objekt am höchsten Punkt ist, ist seine Geschwindigkeit Null. Wenn es zu seinem Ausgangspunkt zurückgekehrt ist, ist seine Verschiebung Null.
Für die obige Frage gilt:
$u \ = \ \mathrm {-30 \ \frac {m}{s}}$, $a \ = \ \mathrm {+10 \ \frac {m}{s^2}}$, $s \ = \ 0$ und $t$ ist zu bestimmen.
Wir verwenden also die Gleichung:
$s \ = \ ut \ + \ \frac {1}{2} \ at^2 $
und lassen der Einfachheit halber die Einheiten weg:
$0 \ = \ - 30 \ t \ + (\frac {1}{2} \ \cdot \ 10 \ \cdot \ t^2)$
Umgestellt und vereinfacht ergibt sich:
$t(t \ - \ 6) \ = \ 0$
Dies hat zwei Lösungen zur Folge: $t \ = \ 6$ und $t \ = \ 0$
So schlägt die Billard-Kugen nach 6 Sekunden wieder auf Boden auf. (Das Ergebnis $t \ = \ 0$ tritt auf, weil die Kugel auch null Verschiebung hatte, als sie zum ersten Mal geworfen wurde.)
Nach unten und zur Seite
Auf dem Bild unten siehst du was passiert, wenn eine Billard-Kugel fallen gelassen wird und eine andere zeitgleich geworfen wird (unter der Annahme, dass es keinen Luftwiderstand gibt). Die Positionen der Kugeln sind in regelmäßigen Zeitabständen dargestellt.

- Die beiden Kugeln haben die gleiche vertikale Bewegung. Beide treffen gleichzeitig auf den Boden, weil beide die gleiche Abwärtsbeschleunigung (g) haben.
- Die zweite Kugel bewegt sich horizontal mit konstanter Geschwindigkeit über den Boden - sie hat eine gleichmäßige horizontale Geschwindigkeit.
Die Merkmale der Bewegung sind oben beschrieben. Ergebnisse wie diese zeigen, dass, wenn ein Objekt frei fällt, seine vertikalen und horizontalen Bewegungen unabhängig voneinander sind.
Beispiel:
Jemand wirft einen Speer horizontal von der Spitze einer Klippe. Berechne den horizontalen Weg des Speers, bevor er auf die Wasseroberfläche trifft. (Wir nehmen an, dass g = 10 $\mathsf {\tfrac {m}{s^2}}$ und dass der Luftwiderstand vernachlässigbar ist.)
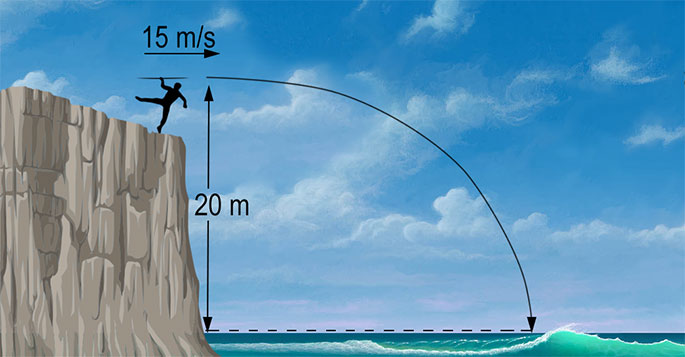
Betrachte zuerst die vertikale Bewegung und ermittle die Zeit, die der Speer benötigen würde, wenn man ihn senkrecht auf die Wasseroberfläche fallen lassen würde. In diesem Fall:
$s \ = \ 20 \ m$ (weil die vertikale Verschiebung des Speers gleich der Höhe der Klippe ist)
$u \ = \ 0$ (weil der Speer am Anfang keine vertikale Geschwindigkeit hat) und
$a \ = \ g \ = \ \mathrm {10 \ \tfrac {m}{s^2}}$.
Wir verwenden die Gleichung:
$s \ = \ ut \ + \ \tfrac {1}{2} \ at^2 $:
$20 \ = \ (0 \ \cdot \ t) + \ (\tfrac {1}{2} \ \cdot \ 10 \ \cdot \ t^2)$
Umgestellt und vereinfacht ergibt sich $t$ = 2 Sekunden.
Als nächstes betrachte die horizontale Bewegung und berechne, wie weit der Speer in 2 $s$ bei einer konstanten horizontalen Geschwindigkeit von 15 $\mathrm {\tfrac {m}{s}}$ fliegen würde (zurückgelegter, horizontaler Weg = horizontale Geschwindigkeit $\cdot$ benötigte Zeit):
Also:
zurückgelegter, horizontaler Weg = $\mathrm {15 \frac {m}{s} \ \cdot \ 2 \ s \ = \ 30 \ m}$