Druck in Flüssigkeiten

Druck und Gewicht - Grundlegendes

Für eine Kraft, die rechtwinklig auf eine Fläche wirkt, gilt folgende Formel:

$\mathsf {Druck \ = \ \tfrac {Kraft}{Fläche}}$

Wenn die Kraft in Newton (N) und die Fläche in Quadratmetern (m²) angegeben wird, dann gibt man den Druck in Pascal (Pa) an.

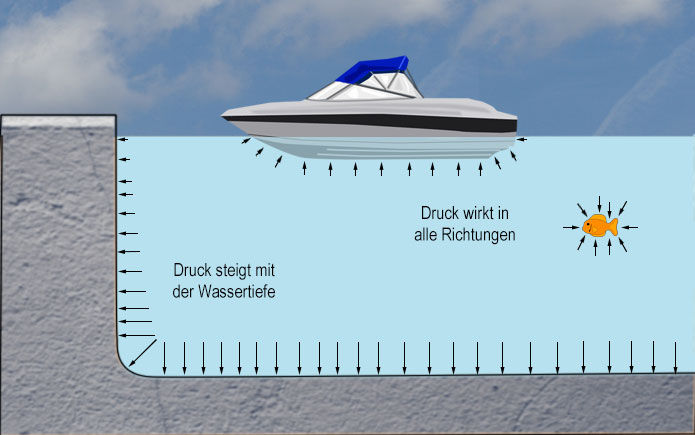
Eine Flüssigkeit wird in ihrem Behälter durch ihr Gewicht gehalten. Dies verursacht Druck auf den Behälter und Druck auf jedes Objekt, das sich in der Flüssigkeit befindet.

Die folgenden Eigenschaften gelten für jede stehende Flüssigkeit in einem offenen Behälter. Die Experimente zeigen zwei von ihnen.

Druck wirkt in alle Richtungen

Die Flüssigkeit drückt auf jede Fläche, die mit ihr in Berührung kommt, egal wohin die Oberfläche zeigt. Zum Beispiel muss das Tiefsee-Schiff unten dem zerquetschenden Effekt des Meerwassers standhalten, das von allen Seiten Druck ausübt, nicht nur nach unten.

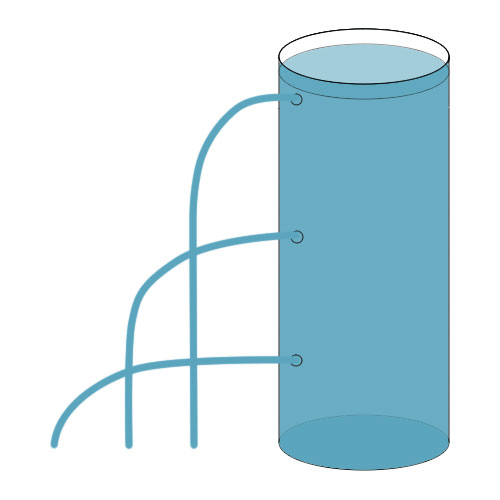
Wasserdruck in einem Behälter mit drei Löchern, Druck nimmt mit der Tiefe zu

Druck steigt mit der Tiefe

Je tiefer ein Objekt in einer Flüssigkeit ist, desto größer ist das Gewicht der Flüssigkeit darüber und desto höher ist der Druck. Dämme an der Unterseite sind dicker, um dem höheren Druck dort zu widerstehen.

Druck hängt von der Dichte der Flüssigkeit ab

Je dichter die Flüssigkeit ist, desto höher der Druck in einer bestimmten Tiefe.

Druck hängt nicht von der Form des Behälters ab

Unabhängig von der Form oder Breite eines Behälters ist der Druck in einer bestimmten Tiefe immer gleich.

Tauchboot Druck wirkt an jeder Stelle — Tiefsee-Tauchboote sind so gebaut, dass sie der zerquetschenden Wirkung des Wassers widerstehen können. Der Wasserdruck wirkt aus allen Richtungen auf das Tauchboot.
Foto: NOAA Photo Library, wikimedia.org

Nützliche Zusammenhänge

Bei Berechnungen ist es immer gut zu wissen, in welcher Beziehung physikalische Größen zueinander stehen:

Volumen (in m³)

Dichte (in $\mathsf {\tfrac {kg}{m^3}}$)

Masse (in kg)

Gewicht (in N)

g (10 $\mathsf {\tfrac {N}{kg}}$)

Es könnte zum Beispiel sein, dass du das Volumen und die Dichte einer Flüssigkeit kennst, aber das Gewicht der Flüssigkeit herausfinden musst. Dazu kannst du die folgenden Gleichungen anwenden:

$\mathrm {Dichte \ = \ \frac {Masse}{Volumen}}$

$\mathrm {Gewicht \ = \ Masse \ \cdot \ g}$

Aus diesen Gleichungen folgt:

$\mathrm { Masse \ = \ Dichte \ \cdot \ Volumen }$

$\mathrm { Gewicht \ = \ Dichte \ \cdot \ Volumen \ \cdot \ g }$

Berechnung des Drucks in einer Flüssigkeit

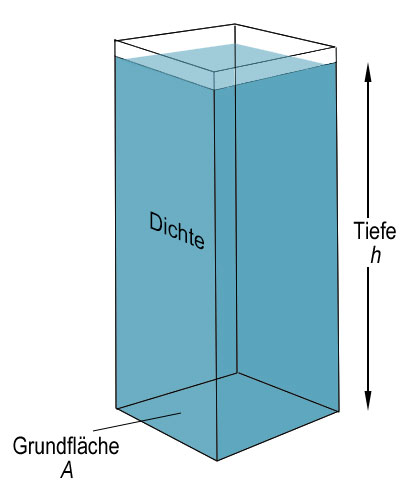
offener Flüssigkeitsbehälter mit Kantenlängen

Der Behälter oben hat die Grundfläche A. Er ist bis zu einer Tiefe h mit einer Flüssigkeit der Dichte $\rho$ (griechischer Buchstabe 'rho') gefüllt. Um den herrschenden Druck auf die Grundfläche (aufgrund der Flüssigkeit) zu berechnen, musst du zuerst das Gewicht der Flüssigkeit kennen:

Volumen der Flüssigkeit =
Grundfläche $\cdot$ Tiefe =
$A \ \cdot \ h$

Masse der Flüssigkeit = Dichte $\cdot$ Volumen =
$\rho \ \cdot \ A \ \cdot \ h$

Gewicht der Flüssigkeit = Masse $\cdot$ g =
$\rho \ \cdot \ g \ \cdot \ A \ \cdot \ h$

Also: Kraft auf Grundfläche = pgAh

Diese Kraft wirkt auf eine Fläche A.

Druck = $\mathsf {\tfrac {Kraft}{Fläche}} \ = \ \tfrac {\rho \cdot g \cdot A \cdot h}{A} \ = \ \rho \cdot \ g \cdot h$

In einer Tiefe h in einer Flüssigkeit der Dichte $\rho$ gilt:

$\mathsf {Druck} \ = \ \rho \cdot \ g \cdot h$

Beispiel

Wenn die Dichte des Wassers 1000 $\mathrm {\tfrac {kg}{m^3}}$ ist, wie hoch ist der Wasserdruck in einem 2 m tiefen Schwimmbecken?

$\mathsf {Druck} \ = \ \rho \cdot \ g \cdot h \ = \ \mathrm {1000 \ \tfrac {kg}{m^3} \ \cdot 10 \ \tfrac {N}{kg} \ \cdot \ 2 \ m \ = \ 20000 \ Pa}$

Fragen

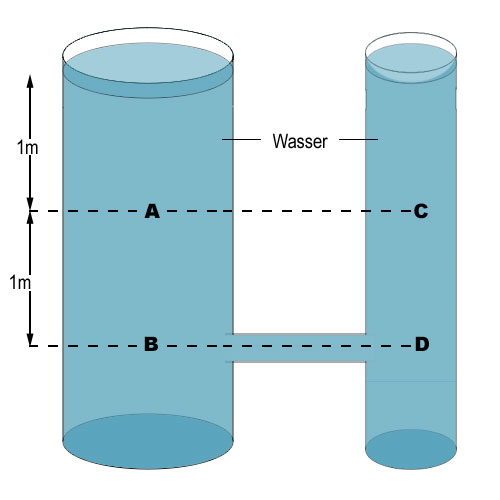
Wasserbehälter mit Angaben zu den Abmessungen