Schwerpunkt

Wie alle anderen Gegenstände auch besteht der Balken (unten) aus vielen winzigen Partikeln, auf die jeweils kleine Gravitationskräfte wirken. Der Balken ist ausbalanciert, weil er an einem ganz bestimmten Punkt (G) aufgehängt ist. An diesem Punkt haben die Gravitationskräfte Drehmomente, die sich gegenseitig aufheben.

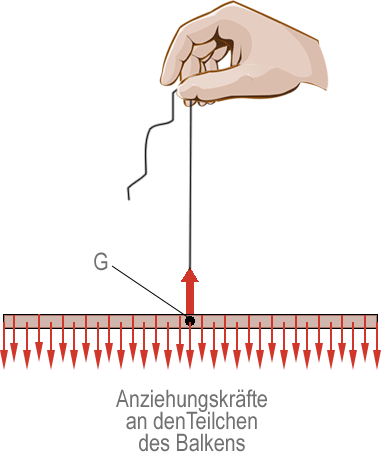
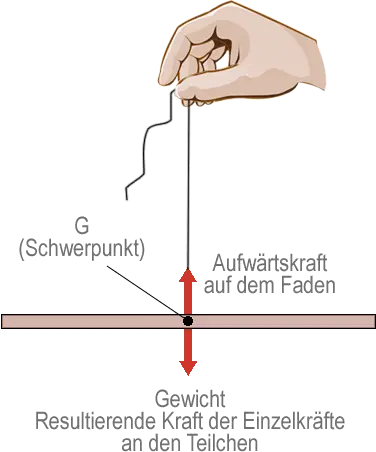
Gemeinsam wirken die kleinen Gravitationskräfte am Punkt G wie eine einzige Kraft. Mit anderen Worten, sie haben bei G eine Resultierende Kraft, und die ist das Gewicht des Balkens. G ist der Schwerpunkt (oder die Mitte der Masse).

Den Schwerpunkt finden

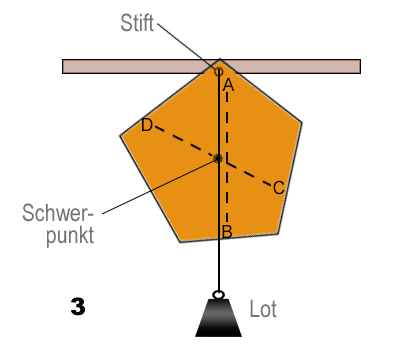
Im Diagramm 1 kann der fünfeckig ausgeschnittene Karton frei um den Befestigungsstift schwingen. Wenn der Karton losgelassen wird, üben die Kräfte eine Drehwirkung auf ihn aus, bis sein Schwerpunkt senkrecht unter dem Stift liegt (siehe Diagramm 2). Unabhängig davon, an welchem Punkt der Karton befestigt wird, er wird immer mit seinem Schwerpunkt vertikal unter dem Stift hängen. Diese Tatsache kann man sich zunutze machen, um den Schwerpunkt zu bestimmen.

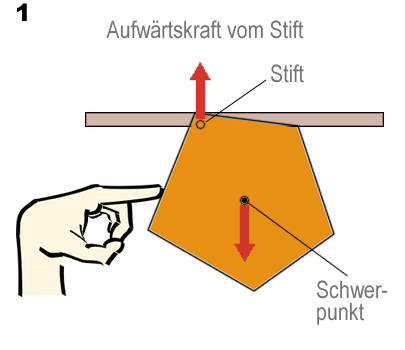
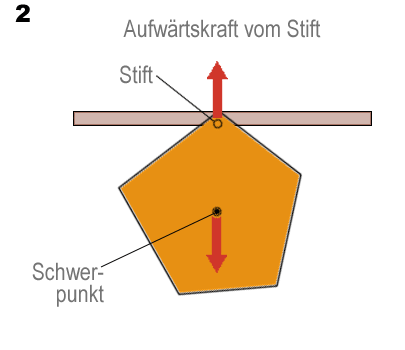
In Diagramm 3 liegt der Schwerpunkt irgendwo auf der senkrechten Linie, die von A nach B verläuft. Wenn der Karton an einem anderen Punkt befestigt wird, kann eine zweite Linie gezogen werden, die von C nach D verläuft. Der Schwerpunkt muss auch auf dieser Linie liegen, und zwar an der Stelle, wo sich die Linien AB und CD kreuzen.

Problem mit einem schweren Balken

Bei einfachen Beispielen wird oft gesagt, dass der ausbalancierte Balken ein vernachlässigbares Gewicht hat. Bei komplizierteren Aufgabenstellungen musst du dieses Gewicht allerdings berücksichtigen.

Beispiel:

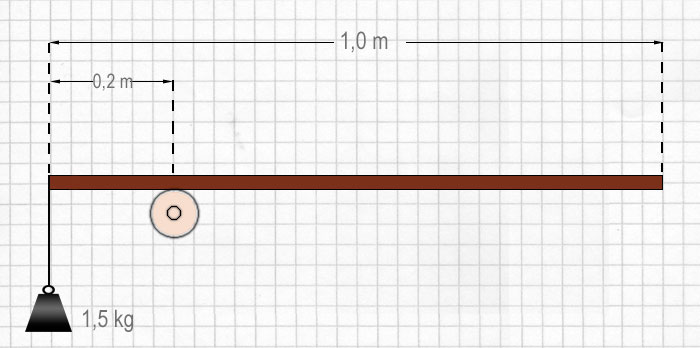
Wenn an einem gleichförmigen und ausbalancierten Balken an einem Ende eine Masse von 1,5 kg hängt, wie groß ist dann sein Gewicht? (g = 10 $\mathrm {\smash{\tfrac {N}{kg}}}$)

Um die Aufgabe zu lösen, zeichne das Diagramm neu, um alle Kräfte und Distanzen aufzuzeigen (wie im unteren Diagramm). Da g = 10 $\mathrm {\smash {\frac {N}{kg}}}$, haben die 1,5 kg Masse ein Gewicht von 15 N.

"Gleichförmig" bedeutet in diesem Fall, dass das Gewicht des Balkens gleichmäßig verteilt ist, so dass der Schwerpunkt des Balkens sich an seinem Mittelpunkt befindet, und zwar 0,5 m vom linken Ende entfernt. An dieser Stelle wirkt das Gewicht W des Balkens.

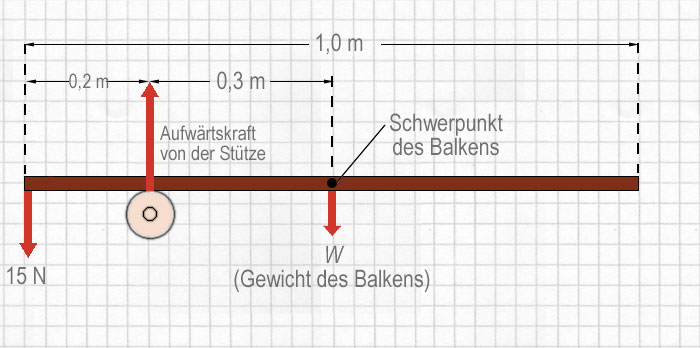
Bestimme nun die Drehmomente um die Stütze o. Die Aufwärtskraft hat um diesen Punkt kein Drehmoment, aber es gibt ein Drehmoment gegen den Uhrzeigersinn:

$\mathrm {15 \ N \ \cdot \ 0,2 \ m}$

und eines im Uhrzeigersinn:

$W \ \cdot \ \mathrm {0,3 \ m}$

Da der Balken im Gleichgewicht ist gilt:

$\mathrm {15 \ N \ \cdot \ 0,2 \ m} \ = \ W \ \cdot \ \mathrm {0,3 \ m}$

Also ist das Gewicht W des Balkens 10 N.

Stabilität

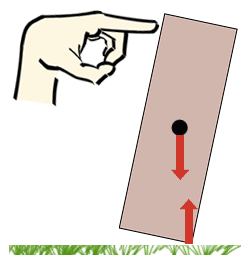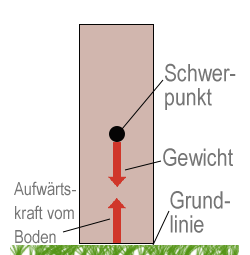
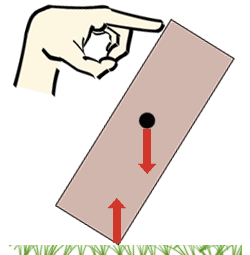
Diese Schachtel ist im Gleichgewicht. Die Kräfte, die auf sie wirken, sind ausgeglichen, ebenso die Drehmomente.	Bei einer kleinen Neigung drehen die Kräfte die Schachtel wieder in ihre ursprüngliche Position.

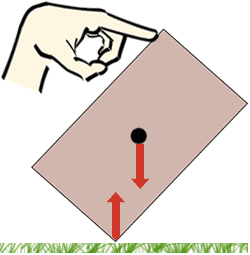Bei einer großen Neigung bewirken die Kräfte, dass die Schachtel umkippt.	Eine Schachtel mit einer breiteren Basis und einem niedrigerem Schwerpunkt kann etwas weiter geneigt werden, bevor sie umkippt.

Wenn die Schachtel oben mit dem Finger nur ein wenig geneigt und dann wieder freigegeben wird, fällt sie wieder in ihre ursprüngliche Position zurück. Die Position war stabil. Wenn die Schachtel etwas weiter geneigt wird, fällt sie um. Sie fängt an zu kippen, sobald sich der Schwerpunkt über den Rand der Basis bewegt. Von da an haben die Kräfte, die auf die Schachtel wirken, einen Dreheffekt, der sie noch weiter kippt. Eine Schachtel mit einer breiteren Basis und/oder einem niedrigeren Schwerpunkt ist stabiler. Sie kann in einem größeren Winkel geneigt werden, bevor sie anfängt zu kippen.

Drei Arten von Gleichgewicht
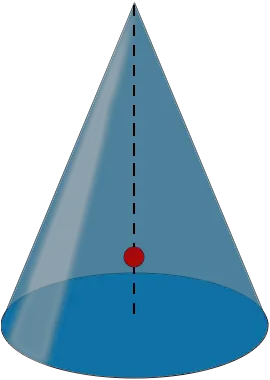
Stabiles Gleichgewicht Wenn du den Kegel ein wenig kippst, bleibt der Schwerpunkt über der Basis. So fällt der Kegel in seine ursprüngliche Position zurück.
Neutrales Gleichgewicht Ohne Krafteinwirkung, bleibt der Ball dort, wo er ist. Wenn er bewegt wird, so bleibt er danach in seiner neuen Position stehen. Wo immer sich der Ball befindet, sein Schwerpunkt liegt immer genau über dem Punkt, der seine "Basis" ist.
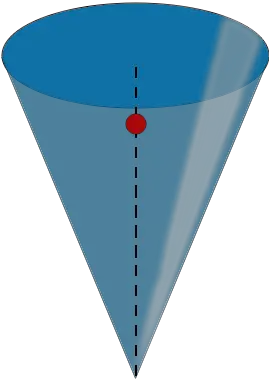
Unstabiles Gleichgewicht Der Kegel ist auch hier im Gleichgewicht, aber nur kurz! Seine spitze "Basis" ist so klein, dass der Schwerpunkt sofort darüber hinausgeht.

Fragen

1. Der Hocker ist gerade im Begriff umzufallen.

1. Zeichne den Hocker nach (oder drucke ihn aus) und zeichne die Lage des Schwerpunkts ein.
2. Wie würdest du den Hocker umbauen, um ihn stabiler zu machen? Nenne zwei Möglichkeiten.

Richtig ist:

2. Man kann ihn breiter machen oder niedriger machen.

2. An einem gleichmäßigen Meterstab hängt an einem Ende ein Gewicht von 4 N. Der Meterstab hält die Waage, wenn er an einem Punkt aufgehängt wird, der 0,1 m von diesem Ende entfernt ist.

1. Zeichne ein Diagramm, um die Kräfte zu zeigen, die auf den Meterstab wirken.
2. Berechne das Gewicht des Meterstabs.

Richtig ist:

1.  
2. 1 N

3. Zeichne ein Diagramm, das einen Bleistift in einem stabilen, instabilen und neutralen Gleichgewicht zeigt.