Bewegungsdiagramme

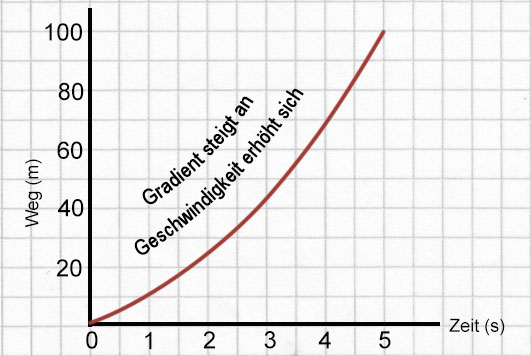
Weg-Zeit Diagramm

 

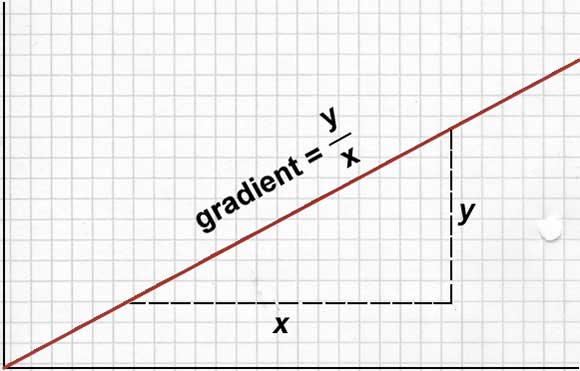
Diagramme können bei der Untersuchung von Bewegungsabläufen sehr hilfreich sein. Auf dem Bild unten fährt ein Auto entlang einer geraden Straße vorbei an einer Laterne. Der Abstand des Autos von der Laterne wird jede Sekunde gemessen. Die Diagramme und Grafiken zeigen vier verschiedene Beispiele dafür, wie sich das Auto bewegen könnte.

In einem Diagramm wird der Anstieg der Linie auf der vertikalen Achse geteilt durch den Anstieg auf der horizontalen Achse als Gradient bezeichnet (siehe links). In einem Weg-Zeit-Diagramm zeigt dir die Steigung an, wie viel zusätzlicher Weg jede Sekunde zurückgelegt wird. Also:

In einem Weg-Zeit-Diagramm ist der Gradient der Linie numerisch gleich der Geschwindigkeit.

A) Das Auto fährt mit konstanter Geschwindigkeit

Zeit (s)	0	1	2	3	4	5
Weg (m)	0	10	20	30	40	50

B) Das Auto fährt mit konstanter Geschwindigkeit, jedoch schneller

Zeit (s)	0	1	2	3	4	5
Weg (m)	0	20	40	60	80	100

C) Der Fahrer tritt aufs Gaspedal, das Auto beschleunigt

Zeit (s)	0	1	2	3	4	5
Weg (m)	0	10	25	45	70	100

D) Der Fahrer hat das Auto abgestellt, es steht.

Zeit (s)	0	1	2	3	4	5
Weg (m)	50	50	50	50	50	50

Geschwindigkeit-Zeit-Diagramme

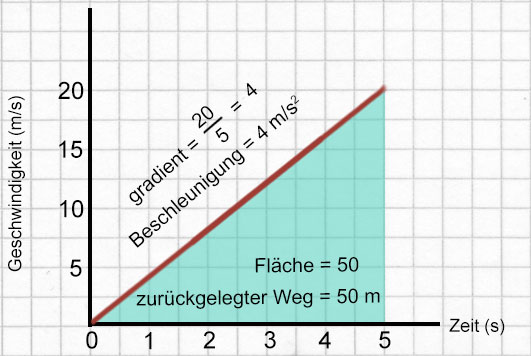
Jedes der beiden Geschwindigkeit-Zeit-Diagramme unten steht für ein Auto, das entlang einer geraden Straße fährt. Die Steigung sagt dir, wie viel Geschwindigkeit jede Sekunde zugelegt wird. Damit:

In einem Geschwindigkeit-Zeit-Diagramm ist der Gradient der Linie numerisch gleich der Beschleunigung.

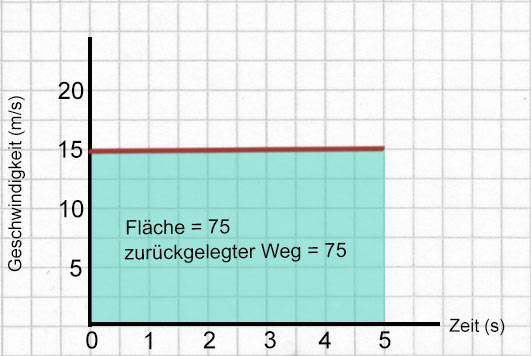
In Grafik E fährt das Auto für 5 s mit einer konstanten Geschwindigkeit von 15 $\mathrm {\tfrac {m}{s}}$, so dass die zurückgelegte Strecke 75 m beträgt. Die Fläche des schattierten Rechtecks, berechnet unter Verwendung der Skalenzahlen, ist ebenfalls 75. Dieses Prinzip funktioniert auch für kompliziertere Diagramme. In Grafik F ist die Fläche des schattierten Dreiecks $\mathsf {\tfrac {1}{2} \cdot \ Grundlinie \ \cdot \ Höhe}$, ergibt 50. Somit ist die zurückgelegte Strecke 50 Meter.

In einem Geschwindigkeit-Zeit-Diagramm ist die Fläche unter der Linie numerisch gleich der zurückgelegten Strecke.

E) Das Auto fährt mit konstanter Geschwindigkeit

Zeit (s)	0	1	2	3	4	5
Geschwin- digkeit (m/s)	15	15	15	15	15	15

F) Der Fahrer bewegt das Auto mit konstanter Beschleunigung

Zeit (s)	0	1	2	3	4	5
Geschwin- digkeit (m/s)	0	4	8	12	16	20