Kreisbewegungen
Zentripetalkraft
Auf dem Bild unten läßt jemand einen Ball an einer Schnur über seinem Kopf in einem horizontalen Kreis mit einer gleichmäßigen Geschwindigkeit kreisen. Da sich der Ball in einer kreisförmigen Bahn bewegt, muß es eine nach innen gerichtete Kraft geben, die den Ball davon abhält, einfach davonzufliegen. Verantwortlich dafür ist die Spannung in der Schnur, die den Ball auf seiner Bahn hält. Wie es Newtons erstes Bewegungsgesetz vorhersagt, würde der Ball ohne diese Kraft in einer geraden Linie davonfliegen. Das ist genau das, was passiert, wenn die Schnur reißt.
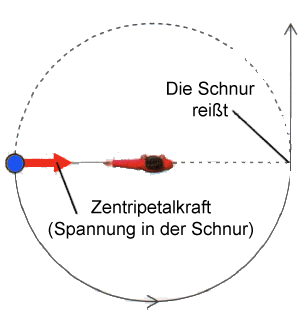
Diese nach innen gerichtete Kraft, die notwendig ist um ein Objekt in einer Kreisbahn zu halten, heißt Zentripetalkraft.
Eine größere Zentripetalkraft ist erforderlich, wenn:
- die Masse des Objekts erhöht wird
- die Geschwindigkeit des Objekts erhöht wird
- der Radius des Kreises verkleinert wird.

Geschwindigkeitsänderung
Ein Objekt muss nicht unbedingt beschleunigen oder verlangsamen, um seine Geschwindigkeit zu ändern. Eine Änderung der Geschwindigkeit kann auch eintreten, wenn das bewegte Objekt seine Richtung ändert:
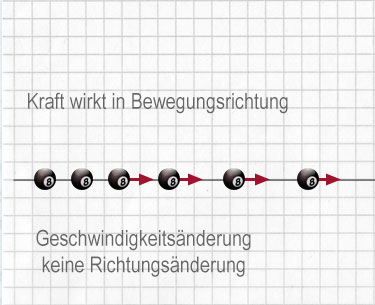
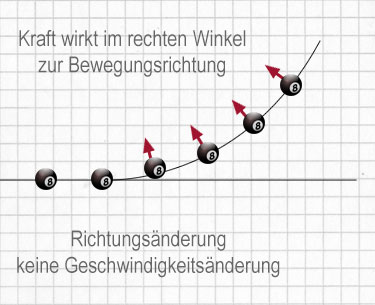
Oben siehst du, wie eine resultierende Kraft eine Geschwindigkeitsänderung bewirken kann. Das Bild rechts zeigt, was bei einer kreisförmigen Bewegung geschieht.
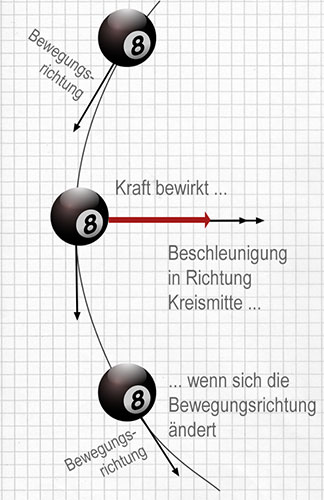
Zentripetalkräfte werden nicht durch Kreisbewegungen erzeugt. Die Zentripetalkraft ist die Kraft, die aufgewendet werden muss, um ein Objekt in einem Kreis zu bewegen, anstatt in einer geraden Linie.
... und Zentrifugalkraft
Wenn du einen Ball an einer Schnur über deinem Kopf kreisen läßt, fühlst du eine nach außen ziehende Kraft in deiner Hand. Diese Kraft wirkt nicht auf den Ball selbst, denn wenn die Schnur reißt, bewegt sich der Ball entlang einer Tangente. Er wird also nicht nach außen geschleudert
Wenn sich die Geschwindigkeit eines Objekts in irgendeiner Weise ändert, beschleunigt das Objekt. Der Vektor der Beschleunigung zeigt in die gleiche Richtung wie die resultierende Kraft.
Beschleunigung nach innen
Die Bewegung eines Objekts auf einer Kreisbahn ist ein Beispiel für eine Kraft, die eine Beschleunigung bewirkt.
Wenn sich etwas in einem Kreis bewegt, erzeugt die innere Zentripetalkraft eine nach innen gerichtete Beschleunigung (Bild rechts). Es kann schwierig sein, sich einen Ball vorzustellen, der in Richtung der Mitte eines Kreises beschleunigt, ohne dieser Mitte näher zu kommen. Aber der Ball bewegt sich tatsächlich konstant nach innen, und zwar von der Position aus, die er gehabt hätte, wenn er in einer geraden Linie sich bewegte.
Satelliten in der Umlaufbahn
Die Anziehungskraft der Erde (Gravitation) bewirkt eine Zentripetalkraft, die der Grund dafür ist, warum sich Satelliten in einer Kreisbahn um die Erde zu bewegen. Wenn ein Satellit in eine kreisförmige Umlaufbahn gebracht wird, hat man vorher seine Geschwindigkeit sorgfältig festgelegt, so dass sein Gewicht genau die richtige Zentripetalkraft liefert.
Die Masse eines Satelliten beeinflusst nicht die Geschwindigkeit, die für eine bestimmte Umlaufbahn erforderlich ist. Wenn die Masse des Satelliten verdoppelt würde, so ist zwar doppelt so viel Zentripetalkraft erforderlich, aber die wird durch die dann doppelte Anziehungskraft der Erde erzeugt.
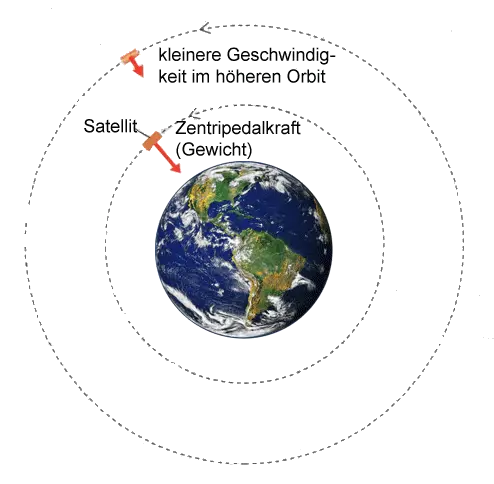
Die Zeit für eine Umlaufbahn nennt man Periode $(T)$. Sie ist mit der Geschwindigkeit des Satelliten $(v)$ und dem Radius $(r)$ seiner Umlaufbahn durch folgende Gleichung verbunden:
$T \ = \ \frac {2 \ \cdot \ \Large \pi \ \cdot \ r}{\Large v}$
Umso größer ist der Radius der Umlaufbahn, und je langsamer die Geschwindigkeit, desto länger die Periode.
Berechnung der ...
...Zentripetalbeschleunigung
Es gibt eine Gleichung zur Berechnung der Zentripetalbeschleunigung. Wenn sich ein Objekt mit der Geschwindigkeit v im Kreis des Radius r bewegt, dann gilt:
Zentripetalbeschleunigung = $\mathrm {\frac {v^2}{r}}$
Anmerkung: Wenn sich das Objekt in einer Kreisbahn mit kleinerem Radius schneller bewegt, dann erhöht sich seine Zentripetalbeschleunigung.
... und Zentripetalkraft
Kraft = Masse $\cdot$ Beschleunigung.
Also, wenn das Objekt, das sich in einem Kreis bewegt, eine Masse m hat, dann:
Erforderliche Zentripetalkraft = $\mathrm {\frac {mv^2}{r}}$
Fragen
Richtig ist:
Richtig ist:
die Reibung zwischen den Reifen und der Straße
Richtig ist:
- sie wäre kleiner
- sie ist kleiner
- sie ist größer
Richtig ist:
- die Geschwindigkeit würde gleich bleiben
- die Geschwindigkeit wäre niedriger
- die Zentripetalkraft wäre niedriger