Anpassungsdämpfung: Unterschied zwischen den Versionen

Aktuelle Version vom 4. August 2021, 17:51 Uhr

Anpassungsdämpfung (engl.: matching attenuation) ist in der Hochfrequenztechnik eine Dämpfung durch Reflexion. Die Anpassungsdämpfung tritt auf, wenn eine Leitung nicht mit ihrer Wellenimpedanz abgeschlossen ist oder Leitungen mit unterschiedlichen Wellenimpedanzen gekoppelt werden. Am Ort der Fehlanpassung entsteht im Hochfrequenzbereich durch Reflexion eine zum Leitungsanfang zurück laufende Welle als Störung.

Teilweise Reflexion und Transmission eines Impulses an der sprunghaften Änderung der Wellenimpedanz. Der Anteil der reflektierten und transmittierten Intensität hängt vom Unterschied der Wellenimpedanzen ab

Bei jeder Schnittstelle bildet der Ausgangswiderstand der Quelle mit dem Eingangswiderstand der Last eine Anpassungsdämpfung, die auch Schnittstellendämpfung genannt wird. Mit

R_{\mathrm {i} }

= Innenwiderstand der Quelle

R_{\mathrm {a} }

= Außenwiderstand der Last

ist die Anpassungsdämpfung $$ r $$

r={\frac {R_{\mathrm {a} }}{R_{\mathrm {a} }+R_{\mathrm {i} }}}

und das Anpassungsdämpfungsmaß

\Delta L=\ln {\frac {1}{r}}=-20\;\lg r{\text{ dB}}

In der Tontechnik

Eine Anpassungsdämpfung gibt es auch im Audio-Bereich, also in der Tontechnik. Beispielsweise erleidet ein Mikrofon, das in den Eingang einer Soundkarte gesteckt wird eine Anpassungsdämpfung. Wie gut, wenn das Mikrofon niederohmig ist, also einen niedrigen Ausgangswiderstand (Quellwiderstand $R_{\mathrm {i} }$ , Innenwiderstand) von 50 Ω besitzt und es sich um Niederfrequenz im Hörbereich bis maximal 40 kHz (Doppelte Hörgrenze) handelt. Als Lastwiderstand $R_{\mathrm {a} }$ tritt der Eingangswiderstand des Mischpults (Mikrofonvorverstärker) mit 1000 bis 2000 Ω auf. Eine Anpassungsdämpfung von kleiner 1 dB ist problemlos.

Besonders ist der wichtige Dämpfungsfaktor bei der Schnittstelle vom Endverstärker mit 0,1 Ω Ausgangswiderstand zum üblichen 8-Ω-Lautsprecher als Anpassungsdämpfung zu beachten. Hier gibt es keine Leistungsanpassung.

Weblinks

@@ Zeile 1: / Zeile 1: @@
 '''Anpassungsdämpfung''' (engl.: ''matching attenuation'') ist in der [[Hochfrequenztechnik]] eine Dämpfung durch [[Reflexion (Physik)|Reflexion]]. Die Anpassungsdämpfung tritt auf, wenn eine Leitung nicht mit ihrer Wellenimpedanz abgeschlossen ist oder Leitungen mit unterschiedlichen Wellenimpedanzen gekoppelt werden. Am Ort der [[Fehlanpassung]] entsteht im Hochfrequenzbereich durch Reflexion eine zum Leitungsanfang zurück laufende Welle als Störung.
-[[Image:Partial transmittance.gif|thumb|300px|Teilweise Reflexion und Transmission eines Impulses an der sprunghaften Änderung der [[Wellenimpedanz]]. Der Anteil der reflektierten und transmittierten Intensität hängt vom Unterschied der Wellenimpedanzen ab]]
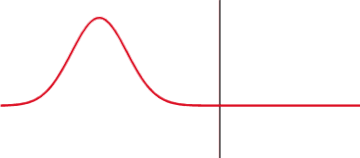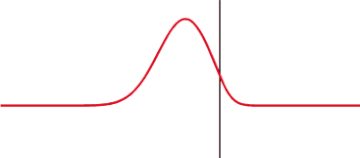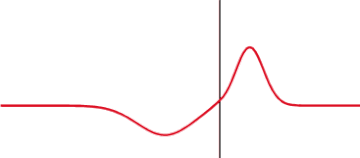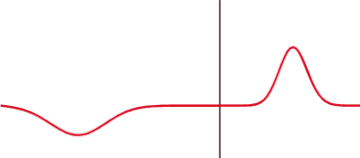
+[[Bild:Partial transmittance.gif|mini|hochkant=1.2|Teilweise Reflexion und Transmission eines Impulses an der sprunghaften Änderung der [[Wellenimpedanz]]. Der Anteil der reflektierten und transmittierten Intensität hängt vom Unterschied der Wellenimpedanzen ab]]
-Bei jeder [[Schnittstelle]] bildet der [[Ausgangswiderstand]] der Quelle mit dem [[Eingangswiderstand]] der Last eine Anpassungsdämpfung, die auch Schnittstellendämpfung genannt wird. Die Anpassungsdämpfung in dB ist:
+Bei jeder [[Schnittstelle]] bildet der [[Ausgangswiderstand]] der Quelle mit dem [[Eingangswiderstand]] der Last eine Anpassungsdämpfung, die auch Schnittstellendämpfung genannt wird. Mit
-:<math>
-\text{Anpassungsdämpfung} = 20 \log \left( \frac{R_\mathrm{a}}{R_\mathrm{a} + R_\mathrm{i}} \right)
-</math>
-wobei gilt:
 :<math>R_\mathrm{i}</math> = Innenwiderstand der Quelle
-:<math>R_\mathrm{a}</math> = Aussenwiderstand der Last
+:<math>R_\mathrm{a}</math> = Außenwiderstand der Last
+ist die Anpassungsdämpfung <math>r</math>
+:<math>r=\frac{R_\mathrm a}{R_\mathrm a + R_\mathrm i}</math>
+und das Anpassungs[[dämpfungsmaß]]
+:<math>\Delta L=\ln \frac1r =-20\;\lg r\text{ dB}</math>
 == In der Tontechnik ==
+Eine Anpassungsdämpfung gibt es auch im Audio-Bereich, also in der [[Tontechnik]]. Beispielsweise erleidet ein Mikrofon, das in den Eingang einer [[Soundkarte]] gesteckt wird eine Anpassungsdämpfung. Wie gut, wenn das Mikrofon niederohmig ist, also einen niedrigen [[Ausgangswiderstand]] (Quellwiderstand <math>R_\mathrm{i}</math>, Innenwiderstand) von 50&nbsp;Ω besitzt und es sich um Niederfrequenz im Hörbereich bis maximal 40&nbsp;kHz (Doppelte Hörgrenze) handelt. Als Lastwiderstand <math>R_\mathrm a</math> tritt der [[Eingangswiderstand]] des [[Mischpult]]s ([[Mikrofonvorverstärker]]) mit 1000 bis 2000&nbsp;Ω auf. Eine Anpassungsdämpfung von kleiner 1&nbsp;dB ist problemlos.
-Eine Anpassungsdämpfung gibt es auch im Audio-Bereich, also in der [[Tontechnik]]. Beispielsweise erleidet ein Mikrofon, das in den Eingang einer [[Soundkarte]] gesteckt wird eine Anpassungsdämpfung. Wie gut, wenn das Mikrofon niederohmig ist, also einen niedrigen [[Ausgangswiderstand]] (Quellwiderstand <math>R_\mathrm{i}</math>, Innenwiderstand) von 50&nbsp;Ohm besitzt und es sich um Niederfrequenz im Hörbereich bis maximal 40&nbsp;kHz (Doppelte Hörgrenze) handelt. Als Lastwiderstand Ra tritt der [[Eingangswiderstand]] des [[Mischpult]]s ([[Mikrofonvorverstärker]]) mit 1000 bis 2000&nbsp;Ohm auf. Eine Anpassungsdämpfung von kleiner 1&nbsp;dB ist problemlos.
+Besonders ist der wichtige [[Dämpfungsfaktor]] bei der Schnittstelle vom [[Endverstärker]] mit 0,1&nbsp;Ω Ausgangswiderstand zum üblichen 8-Ω-Lautsprecher als Anpassungsdämpfung zu beachten. Hier gibt es keine [[Leistungsanpassung]].
-Besonders ist der wichtige [[Dämpfungsfaktor]] bei der Schnittstelle vom [[Endverstärker]] mit 0,1&nbsp;Ohm Ausgangswiderstand zum üblichen 8-Ohm-Lautsprecher als Anpassungsdämpfung zu beachten. Hier gibt es keine [[Leistungsanpassung]].
-==Weblinks==
+== Weblinks ==
 *[http://www.sengpielaudio.com/Rechner-anpassungsdaempfung.htm Berechnung der Anpassungsdämpfung]
 *[http://www.sengpielaudio.com/Rechner-spannungsanpassung.htm Zusammenschaltung von zwei Geräten - Anpassungsdämpfung bei einer Schnittstelle beim Aufeinandertreffen von Ri und Ra]