Steinmetzformel

Mit der Steinmetz-Formel lassen sich Kernverluste induktiver Bauelemente berechnen. Sie trägt den Namen ihres Entdeckers, des deutsch-amerikanischen Ingenieurs Karl Steinmetz, der als erstes diese Verluste durch Hysterese und Wirbelströme berechnete.^[1]

Entdeckung der Formel

Wirbelströme, die in den Eisenkernen von Transformatoren sowie den eisernen Spulenkörpern von Generatoren beziehungsweise Elektromotoren auftreten, verursachten in den Anfängen der Elektrotechnik große Probleme, weil sie zum einen den Wirkungsgrad der Anlagen verschlechterten und zum anderen zu einer Erwärmung der Bauteile führten. Der Aufbau der Spulenkörper aus voneinander isolierten Eisenplättchen anstelle eines massiven Eisenkörpers verringerte zwar die Wirbelströme, dennoch wurde in den Transformatoren viel elektrische Energie in Wärme umgewandelt. Weil nämlich die Eisenkerne des Transformators unter dem Einfluss des magnetischen Wechselfeldes der Spulen magnetisiert werden und die Magnetisierung nicht vollständig zurückgeht, wenn das Magnetfeld seine Richtung im Takt der Wechselstrom-Frequenz ändert, bleibt eine Restmagnetisierung bestehen. Die sogenannte Remanenz muss durch das umgepolte Magnetfeld erst überwunden werden, woraus die zusätzlichen Wärmeverluste entstehen. Die Lösung hierfür fand Karl Steinmetz in der Hysterese.^[1]

Hysterese-Kurve

typische Hysteresekurve

Die Atome ferromagnetischer Materialien haben ein magnetisches Moment. Im unmagnetisierten Zustand sind die magnetischen Momente der Atome in alle Raumrichtungen ausgerichtet, wobei Atome in begrenzten Zellen (Weiß’sche Zellen) eine Vorzugsrichtung aufweisen. Die Grenzen dieser Zellen bezeichnet man als Blochwände. Legt man nun ein externes magnetisches Feld an, werden die magnetischen Momente entlang der Magnetfeldrichtung ausgerichtet, indem die Weiß’schen Zellen mit magnetischem Moment in Feldrichtung auf Kosten benachbarter Zellen wachsen. Man spricht auch vom Verschieben von Blochwänden. In bestimmten Grenzen ist dies ein reversibler Prozess. Bei Erhöhung der Feldstärke springen die Blochwände von Fehlstelle zu Fehlstelle, was nicht mehr reversibel ist. Sind alle Zellen ausgerichtet, werden bei einer weiteren Erhöhung des Magnetfeldes die magnetischen Momente aus ihrer Kristallrichtung in die Feldrichtung gedreht. Dieses Verhalten, man spricht hier von Drehprozessen, spiegelt sich in der Hysterese-Kurve (auch B-H-Kurve genannt) wider, deren Verlauf materialabhängig ist.

Im unteren Bereich der Neukurve herrschen reversible Blochwand-Verschiebungen vor. Im mittleren Bereich, in dem die magnetische Flussdichte $ B $ nahezu linear mit der magnetischen Feldstärke $ H $ wächst, erkennt man die irreversiblen Sprünge der Blochwände. Im Sättigungsbereich, bei dem das Ansteigen der magnetischen Flussdichte sehr viel langsamer erfolgt, herrschen die Drehprozesse vor. Zum Erreichen der Sättigungsflussdichte muss eine Sättigungsfeldstärke $ H_{s} $ anliegen. Bei Reduzierung der Feldstärke bleiben viele der verschobenen Blochwände an Fehlstellen hängen, die magnetische Flussdichte nimmt entlang einer anderen Kurve ab. Es ist noch magnetischer Fluss vorhanden, auch wenn die Feldstärke auf Null zurückgegangen ist. Um die sogenannte Remanenzflussdichte $ B_{R} $ auf Null zurückzusetzen, muss man eine bestimmte negative Feldstärke aufbringen, die Koerzitivfeldstärke $ H_{C} $.^[2]

Steinmetzformel bei sinusförmiger Erregung

Steinmetz erkannte, dass die Fläche innerhalb der Hysterese-Kurve den Kernverlusten (in mW pro cm³) pro Zyklus entspricht und setzte diese Tatsache in folgende Formel um:

$ P_{core}=k\cdot f^{a}\cdot B^{b} $

Dabei ist $ P_{core} $ die mittlere Verlustleistung pro Volumeneinheit, $ B $ der Spitzenwert der Induktion, $ k $ die Kernkonstante und $ f $ die Frequenz der sinusförmigen Messspannung. Die Koeffizienten $ a $ und $ b $ sind materialabhängig. Bei Ferriten beispielsweise liegt der Koeffizient $ a $ zwischen 1,1 und 1,9, der Koeffizient $ b $ im Bereich von 1,6 bis 3.^[2]

Anhand der „einfachen“ Steinmetz-Formel lassen sich die Kernverluste von Induktivitäten berechnen, deren Kernbauformen auf Industriestandard basieren. Diese Standardkerne weisen die gleiche Geometrie auf, weshalb auch ihre Kernkonstanten identisch sind. Lediglich die entsprechenden Materialcharakteristika müssen in die Gleichung eingesetzt werden. Eine Ausnahme dabei bilden allerdings Komposit-Induktivitäten, denn auch bei gleicher Kerngröße variieren bei diesen Bauelementen die Geometrieparameter je nach Induktivitätswert. Der Grund: Anders als bei Ringkernkonstruktionen oder den sogenannten E-Kernen wird bei einer Komposit-Induktivität der Kupferdraht zunächst zu einer Luftspule gewickelt. Da jede Spule einen anderen Durchmesser und eine andere Höhe aufweist, gelten für jede Induktivität andere Geometrieparameter und die Kernkonstanten müssen individuell ermittelt werden.^[3]

Steinmetzformel bei nichtsinusförmiger Erregung

Komposit-Induktivitäten werden häufig in nicht galvanisch getrennten DC/DC-Wandlern eingesetzt, welche nicht mit sinusförmigem Wechselstrom, sondern mit gepulstem Gleichstrom arbeiten. Zu der Tatsache, dass der für den Kernverlust mitverantwortliche Strom nun einen dreieckigen Zeitverlauf ausweist, gesellt sich noch ein weiterer Verlustfaktor: Der Einfluss der Betriebstemperatur. Weil DC/DC-Wandler immer öfter auch bei höheren Umgebungstemperaturen zum Einsatz kommen, muss die Induktivität nicht nur den Temperaturanstieg infolge interner Leistungsverluste verkraften, sondern auch höhere Umgebungstemperaturen. Dies beeinflusst den Eisenkern dahingehend, dass Eisenpulver bei höheren Temperaturen schneller altert, wodurch die Kernverluste steigen. Um die Auswirkungen der thermischen Alterung zu minimieren, empfiehlt es sich, die maximale Betriebstemperatur der Induktivität unter +125 °C zu halten.^[3] Um die Betriebsbedingungen an den oberen Temperaturgrenzen der jeweiligen Anwendung / Schaltung zu bestimmen, kann die für sinusförmige Signale geltende Steinmetz-Formel auch unter Berücksichtigung der vorherrschenden Temperaturen angewandt werden:

$ P_{core}=k\cdot f^{a}\cdot B^{b}(c_{t2}T^{2}-c_{t1}T+c_{t0}) $

$ a $ und $ b $ sind wieder die sogenannten Steinmetz-Frequenz- beziehungsweise Steinmetz-Induktionskoeffizienten, welche für Betriebsbedingungen spezifiziert sind, $ k $, $ c_{t1} $, $ c_{t2} $ und $ c_{t0} $ sind Materialkonstanten, $ f $ die Frequenz und $ T $ die Betriebstemperatur.^[4]

Für nicht sinusförmige Signale gilt:

$ P_{core}=f\cdot k\cdot f_{sin_{e}q}^{a-1}\cdot B^{b}(c_{t2}T^{2}-c_{t1}T+c_{t0}) $

Relativer Fehler

Beispiel für den Fehler der Steinmetzformel bei Duty-Cycle >50 % (f=100 kHz; MnZn-Kern)

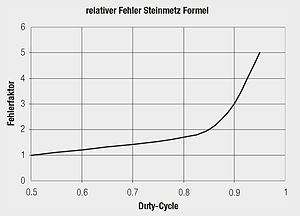
Das sogenannte „Volt-µsec-Produkt“ gibt den Maximalwert an, bis zu dem Speicherdrosseln aufgrund ihrer magnetisch wirksamen Fläche angesteuert werden können. Oder anders ausgedrückt: je höher das Volt-µsec-Produkt, desto höher die Verluste. Mit zunehmender Schaltfrequenz wird das notwendige Vµsec-Produkt der Speicherdrossel geringer; mit steigender Eingangsspannung jedoch größer. Da zur Berechnung der Kernverluste neben dem Volt-µsec-Produkt auch das Tastverhältnis (Duty-Cycle) und die Arbeitsfrequenz der Schaltung essenziell sind, haben diese auch Einfluss auf die Genauigkeit der Steinmetz-Formel. Die Genauigkeit der Steinmetz-Formel ist bei einem Duty-Cycle von 50 % schon geringer, bei kleinen oder großen Duty-Cyclen können Fehler von über 100 % entstehen. Ebenso führen eine Vernachlässigung der Harmonischen oder der DC-Vormagnetisierung zu Ungenauigkeiten bei den errechneten Kernverlusten. Ursachen dafür sind, dass sich eine andere B-H-Kurve einstellt, dass sich ein falsches Vμsec-Produkts ergibt und die Temperaturabhängigkeit nicht berücksichtigt wird.

Verlustberechnung und Softwarewerkzeuge

Um Entwicklern die Auswahl der passenden Induktivitäten zu erleichtern beziehungsweise die in Frage kommenden Bauelemente einzugrenzen, bieten einige Hersteller passiver Bauelemente Tools zur Berechnung an, mit denen sich auch die zu erwartenden Kernverluste ermitteln lassen.

Einzelnachweise