Chemische Welle
- Wikipedia:Vorlagenfehler/Vorlage:Cite journal/Parameter language fehlt
- Biophysik
- Nichtgleichgewichtsthermodynamik
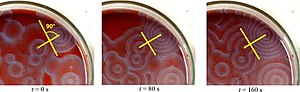
Chemische Wellen sind ein Phänomen der Nichtgleichgewichtsthermodynamik (bzw. der Chemie und Biologie) und ein Spezialfall dissipativer Strukturen.[1] Dabei treten in einem Medium (z. B. einem Reaktionsgemisch oder einer Kolonie von Zellen) räumlich und zeitlich wandernde Konzentrationsänderungen auf, die durch eine selbstverstärkende bzw. positiv rückgekoppelte Reaktion im Medium erzeugt und aufrechterhalten werden. Die Energie für die Aufrechterhaltung kommt nicht wie bei klassischen Wellen (z. B. Schall- oder elektromagnetische Wellen) von außen, sondern aus dem Medium selbst (selbst-erregte Oszillationen). Bekannte Beispiele hierfür sind Konzentrationswellen in oszillierenden chemischen Reaktionen, wie der Belousov-Zhabotinsky-Reaktion,[2] und die Erregungsausbreitung im Herzmuskel.[3]
In Teilgebieten der Physikalischen Chemie und der Theoretischen Biologie wird die Kurzbezeichnung autowave verwendet und auf andere Beispiele für Strukturbildung in aktiven Medien angewandt. Der deutsche Übersetzungsversuch Autowelle ist unüblich. Dabei wurde autowave in Analogie zum englischen auto-oscillations, also selbst-erregte Oszillationen gewählt.[2]
Physikalische Beschreibung
Chemische Wellen treten in Systemen auf, die typischerweise durch ein nicht-lineares, (positiv) rückgekoppeltes Reaktionssystem mit räumlicher Kopplung durch einen Transportprozess charakterisiert sind. In vielen Fällen ist der Transportprozess normale Diffusion. Mathematisch lässt sich ein solches System etwa durch eine Reaktionsdiffusionsgleichung beschreiben. Ohne die Nichtlinearität und Rückkopplung würde das System ohne Musterbildung einem Gleichgewichtszustand zustreben. Ohne die räumlichen Kopplung, wären keine räumlichen Phänomene, wie etwa Wellenausbreitung möglich und es können maximal zeitliche Oszillationen beobachtet werden (z. B. wenn das Reaktionsgemisch einer oszillierenden Reaktion ständig gerührt wird). Für das Auftreten von chemischen Wellen ist weiterhin notwendig, dass sich das Systemen fernab vom thermodynamischen Gleichgewicht befinden. Das bedeutet insbesondere, dass es Energie enthält die für die Strukturbildung aufgewendet werden kann. Dies lässt sich durch eine Entropiebetrachtung verstehen: Geordnete Strukturen, wie etwa Wellen, führen zu einer lokalen Erniedrigung der Entropie. Nach dem 2. Hauptsatz der Thermodynamik ist eine solche Entropieerniedrigung nur möglich, wenn dafür Energie aufgewendet wird. Im hier beschriebenen Fall kommt diese Energie aus der nicht-reversiblen Annäherung des Systems an den stationären Gleichgewichtszustand (z. B. indem nicht-reversible chemische Reaktionen ablaufen), bei der Energie freigesetzt wird. Typischerweise sind chemische Wellen in einem geschlossenen System daher nicht stabil und können nur für eine gewisse Zeit beobachtet werden. Der Vorgang endet, wenn sich das System einem Gleichgewichtszustand nähert bzw. wenn alle Reaktionsedukte verbraucht sind.[1][4] In einem offenen System, ausgehend von einem Fließgleichgewicht, sind chemische Wellen dagegen stabil, da von außen Energie zu ihrer Aufrechterhaltung zugeführt wird (z. B. in Form „frischer“ Reaktionsedukte). Daher können die Wellen immer wieder erregt werden und das System bleibt fern dem Gleichgewicht. In beiden Fällen stammt die Energie für die Strukturbildung also aus dem Medium selbst.
Aufgrund ihres selbst-verstärkenden Charakters genügen schon kleine lokale Störungen, etwa mikroskopische Konzentrations- oder Temperaturunterschiede, beispielsweise das Erhitzen des Reaktionsgemisches mit einer heißen Nadel, um chemische Wellen auszulösen. Daher wird vielfach vom „spontanen Auftreten“ solcher Strukturen gesprochen. Diese Störungen wirken als Erregerzentren, von denen sich Reaktionsfronten ausbreiten. In diesen schreitet die Reaktion in einer anderen Phase voran als im umliegenden Medium. Beispielsweise läuft am Beginn der Front ein erster Reaktionsschritt ab, der zu einem Farbumschlag führt. Die Produkte dieses Schrittes reagieren später weiter und werden teilweise im Sinne einer Autokatalyse wieder zurückgebildet, was zu einem erneuten Farbumschlag führen kann. Verschiedene Teilreaktionen laufen also an verschiedenen Stellen der Front unterschiedlich schnell ab.
Die Sichtbarkeit chemischer Wellen ist oft auf lokale Konzentrationsunterschiede einer farbigen Komponente des Reaktionsgemisches zurückzuführen. Alternativ werden Indikatoren zugegeben, die auf die lokalen Konzentrationen mit einem Farbumschlag reagieren.
Dabei sind chemische Wellen von anderen Phänomenen zu unterscheiden: Es können z. B. rein zeitliche Oszillationen auftreten, die aufgrund der fehlenden räumlichen Ausbreitung keine Welle darstellen. Auch rein räumliche, zeitlich stationäre Muster, sogenannte Turing-Muster sind davon verschieden.[5][6] Alle diese Phänomene werden oft unter dem Begriff Dissipative Strukturen zusammengefasst,[1] für deren Untersuchung Ilya Prigogine 1977 den Nobelpreis für Chemie erhielt. Gerhard Ertl erhielt 2007 den Nobelpreis für Chemie unter anderem für die Untersuchung von chemischen Wellen bei der Oxidation von Kohlenmonoxid auf Platin-Oberflächen.[7]
Eigenschaften
Als Lösung einer nicht-linearen Differentialgleichung weisen chemische Wellen einige Eigenschaften auf, die sie von den üblichen "linearen Wellen" (z. B. Wasserwellen, Licht und andere elektromagnetische Wellen) unterscheiden. In anderen Eigenschaften ähneln sie sich:
- Analog zu konventionellen Wellen können in diesen sich ausbreitenden Mustern meist eine Wellenlänge, Frequenz und Ausbreitungsgeschwindigkeit definiert werden.
- Treffen zwei gegenläufige chemische Wellenfronten aufeinander, so löschen sie sich gegenseitig oft aus, während sich konventionelle Wellen ungestört überlagern. Das Superpositionsprinzip gilt also nicht, wie der nicht-lineare Charakter der beschreibenden Differentialgleichung zeigt.
- Für bestimmte chemische Wellen wurden Reflexions- und Brechungsphänomene beobachtet, die sich in einigen Punkten von analogen Eigenschaften linearer Wellen unterscheiden.[8][9][10]
- Als besondere Wellenform treten Spiralwellen auf, Vortexwellen oder (bei dreidimensionalen Wellen) auch scrollwaves genannt.[3][7][11]
Beispiele

Chemische Wellen können in vielen Systemen beobachtet werden:
- nicht-homogenisierte (nicht-gerührte) Ansätze oszillierender Reaktionen, wie der Belousov-Zhabotinsky-Reaktion[2] oder etwa der Oxidation arseniger Säure mit Iodat[12]
- bei der Oxidation von Kohlenstoffmonoxid auf Platin-Oberflächen[7] werden solitonische Wellen[13] beobachtet
- biochemische Weiterleitung von Impulsen im Nervensystem
- Ausbreitung des Schleimpilzes Dictyostelium discoideum[14]
- Erregungswellen im Herzmuskel[3]
- Modelle zur Musterbildung (z. B. Farbmuster auf Muschelschalen) in biologischen Organismen[15][16]
- Ein einfaches und oft diskutiertes theoretisches Beispiel für ein autokatalytisches Reaktionssystem, das mit einem Diffusionsterm Wellenausbreitung zeigt, ist der sogenannte Brüsselator (siehe Animation rechts).
- Hantz-Reaktionen, eine Klasse von musterbildenden Präzipitationsreaktionen in Gelen, die ein Reaktionsdiffusionssystem implementieren
Es gibt einige nicht-chemische Vorgänge, die eine ähnliche Phänomenologie zeigen und durch ähnliche Differentialgleichungen beschrieben werden können:
- die „Stadionwelle“ La ola (die Fans sind zugleich Erreger und Übermittler)[17]
- Staubildung im Straßenverkehr[18]
- viele zelluläre Automaten zeigen Wellenphänomene, die chemischen Wellen entsprechen,[19] z. B. Conways Spiel des Lebens oder Wator
Einzelnachweise
- ↑ 1,0 1,1 1,2 Dilip Kondepudi, Ilya Prigogine: Modern Thermodynamics. From Heat Engines to Dissipative Structures. John Wiley & Sons, Chichester u. a. 1998, ISBN 0-471-97393-9.
- ↑ 2,0 2,1 2,2 A.M. Zhabotinsky, A.N. Zaikin: Autowave processes in a distributed chemical system. In: Journal of Theoretical Biology. 40. Jahrgang, Nr. 1, Juli 1973, S. 45–61, doi:10.1016/0022-5193(73)90164-1.
- ↑ 3,0 3,1 3,2 Jorge M. Davidenko, Arcady V. Pertsov, Remy Salomonsz, William Baxter, José Jalife: Stationary and drifting spiral waves of excitation in isolated cardiac muscle. In: Nature. 355. Jahrgang, Nr. 6358, 23. Januar 1992, S. 349–351, doi:10.1038/355349a0.
- ↑ Irving Robert Epstein, John Anthony Pojman: An Introduction to Nonlinear Chemical Dynamics. Oscillations, Waves, Patterns, and Chaos Oxford University Press, 1998, ISBN 0-19-509670-3
- ↑ A. M. Turing: The Chemical Basis of Morphogenesis. In: Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences. 237. Jahrgang, Nr. 641, 14. August 1952, S. 37–72, doi:10.1098/rstb.1952.0012 (jstor.org).
- ↑ Mikhail Bushev: Synergetics: Chaos, Order, Self-Organization. World Scientific, 1994, ISBN 981-02-1286-0, S. 6 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ 7,0 7,1 7,2 S. Jakubith, H. Rotermund, W. Engel, A. von Oertzen, G. Ertl: Spatiotemporal concentration patterns in a surface reaction: Propagating and standing waves, rotating spirals, and turbulence. In: Physical Review Letters. Band 65, Nr. 24, Dezember 1990, S. 3013–3016, doi:10.1103/PhysRevLett.65.3013.
- ↑ Anatol M. Zhabotinsky, Matthew D. Eager, Irving R. Epstein: Refraction and reflection of chemical waves. In: Physical Review Letters. 71. Jahrgang, Nr. 10, 1993, S. 1526–1529, doi:10.1103/PhysRevLett.71.1526 (brandeis.edu [PDF]).
- ↑ Joaquim Sainhas, Rui Dilão: Wave Optics in Reaction-Diffusion Systems. In: Physical Review Letters. 80. Jahrgang, Nr. 23, S. 5216–5219, doi:10.1103/PhysRevLett.80.5216.
- ↑ Lingfa Yang, Irving R. Epstein: Chemical Wave Packet Propagation, Reflection, and Spreading. In: The Journal of Physical Chemistry A. 106. Jahrgang, Nr. 47, 2002, S. 11676–11682, doi:10.1021/jp0260907 (brandeis.edu [PDF]).
- ↑ Arthur T. Winfree: Spiral Waves of Chemical Activity. In: Science. 175. Jahrgang, Nr. 4022, 2. November 1972, S. 634–636, doi:10.1126/science.175.4022.634 (sciencemag.org).
- ↑ Adel Hanna, Alan Saul, Kenneth Showalter: Detailed studies of propagating fronts in the iodate oxidation of arsenous acid. In: Journal of the American Chemical Society. Band 104, Nr. 14, Juli 1982, S. 3838–3844, doi:10.1021/ja00378a011.
- ↑ M. Baer, M. Eiswirth, H.-H. Rotermund, G. Ertl: Solitary-wave phenomena in an excitable surface reaction. In: Physical Review Letters. Band 69, Nr. 6, August 1992, S. 945–948, doi:10.1103/PhysRevLett.69.945.
- ↑ K. Tomchik, P. Devreotes: Adenosine 3',5'-monophosphate waves in Dictyostelium discoideum: a demonstration by isotope dilution--fluorography. In: Science. Band 212, Nr. 4493, 24. April 1981, S. 443–446, doi:10.1126/science.6259734.
- ↑ A. Gierer, H. Meinhardt: A theory of biological pattern formation. In: Biological Cybernetics. 12. Jahrgang, Nr. 1, 1972, S. 30–39, doi:10.1007/BF00289234.
- ↑ Hans Meinhardt; Przemyslaw Prusinkiewicz (Hrsg.): The algorithmic beauty of sea shells, Berlin, New York: Springer Verlag, 2003., ISBN 978-3-540-44010-9 (Deutsche Ausgabe: Wie Schnecken sich in Schale werfen).
- ↑ I. Farkas, D. Helbing, T. Vicsek: Social behaviour: Mexican waves in an excitable medium. In: Nature. 419. Jahrgang, Nr. 6903, 12. September 2002, S. 131–132, doi:10.1038/419131a (nature.com).
- ↑ Takashi Nagatani: Density waves in traffic flow. In: Physical Review E. 61. Jahrgang, Nr. 4, 1. April 2000, S. 3564–3570, doi:10.1103/PhysRevE.61.3564.
- ↑ Jörg R Weimar: Simulation with cellular automata Berlin : Logos-Verlag, 2003., ISBN 3-89722-026-1.