Anti-de-Sitter-Raum

Der Anti-de-Sitter-Raum (AdS) ist eine Raumzeit mit negativer kosmologischer Konstante. Die Namensgebung erfolgte als Gegenstück (positive kosmologische Konstante) zum De-Sitter-Raum, benannt nach dem niederländischen Astronomen Willem de Sitter. Die Energieform des Anti-de-Sitter-Raumes ist im Gegensatz zum De-Sitter-Raum anziehend. Dies entspricht der üblichen Wirkung von Gravitation.

Der Anti-de-Sitter-Raum ähnelt dem hyperbolischen Raum zuzüglich einer zeitlichen Dimension. Im Gegensatz zu unserem Universum kann ein Anti-de-Sitter-Raum weder expandieren noch kontrahieren – er sieht zu allen Zeiten gleich aus.

Trotz dieses Unterschieds erweist sich der Anti-de-Sitter-Raum als sehr nützlich bei der Suche nach Quantentheorien für Raumzeit und Gravitation. So ist das Universum in den Randall-Sundrum-Modellen ein fünfdimensionaler Anti-de-Sitter-Raum.

Definition

2-dimensionaler Anti-de-Sitter-Raum. Die Zeit wächst in azimutaler Richtung.

Der $ d $-dimensionale Anti-de-Sitter-Raum ist definierbar als das Hyperboloid

$ u^{2}+v^{2}=\left(a^{2}+\mathbf {x} ^{2}\right)/c^{2}, $

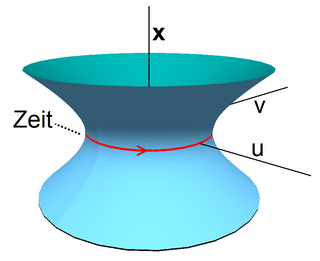
mit Linienelement $ {d\tau }^{2}=du^{2}+dv^{2}-d\mathbf {x} ^{2}/c^{2} $. Hierbei ist $ \mathbf {x} $ ein $ d-1 $-dimensionaler isotroper räumlicher Vektor, $ a $ ist eine Konstante, $ c $ ist die Lichtgeschwindigkeit. Für konstantes $ \mathbf {x} $ besteht der Anti-de-Sitter-Raum aus einem Kreis parallel zur $ u-v $-Ebene, d.h. die Zeit verläuft in einem Kreis $ S^{1} $ um das Hyperboloid.

Die Topologie des AdS-Raums ist $ S^{1}\times \mathbb {R} ^{d-1} $. Dass die Zeit zyklisch ist, ist kein Problem, da man anstelle des Hyperboloids auch seine universelle Überlagerung verwenden kann.

Die intrinsische Struktur des AdS-Raums kommt besser durch sogenannte globale Koordinaten $ (t=a\arctan \left(v/u\right),r=\mathbf {\left|x\right|} ,{\hat {\mathbf {\Omega } }}_{d-2}=\mathbf {x} /r) $ zum Ausdruck, d.h. $ u={\sqrt {a^{2}+r^{2}}}\cos \left(t/a\right) $, $ v={\sqrt {a^{2}+r^{2}}}\sin \left(t/a\right). $ Zur Vereinfachung ist hier $ c=1 $ gesetzt. Die Zeitvariable $ t $ ist zunächst $ 2\pi a $-periodisch. Das Linienelement wird

$ d\tau ^{2}=\left(1+r^{2}/a^{2}\right)dt^{2}-\left(1+r^{2}/a^{2}\right)^{-1}dr^{2}-r^{2}d\Omega _{d-2}^{2}, $

wobei $ d\Omega _{d-2}^{2} $ das Linienelement der $ d-2 $ -dimensionalen Einheitssphäre ist.

Penrose-Diagramm des Anti-de-Sitter-Raums. Die radiale Richtung ist konform auf ein endliches Intervall kompaktifizert. Alle Geodäten sind periodisch in der Zeit. Masselose Teilchen bewegen sich in diagonaler Richtung und erreichen in einer Periode 2mal den Rand.

Der kausale Zusammenhang des AdS-Raums ist aus seinem Penrose-Diagramm ersichtlich. Dieses entsteht aus den globalen Koordinaten mit Hilfe von $ r=\tan(\rho ) $. Die $ \rho $-Koordinate kompaktifiziert die radiale Richtung auf das Intervall $ |\rho |\leq \pi /2 $, das Linienelement erhält bis auf einen konformen Faktor Minkowski-Form. Für Anwendungen ist von Bedeutung, dass der Rand von AdS zeitartig ist, und damit als Bühne eines $ d-1 $-dimensionalen physikalischen Modells in Frage kommt.

Poincaré-Koordinaten

Dieser Typ intrinsischer Koordinaten $ \left\{X^{1},...,X^{d}\right\} $ beschreibt nur eine Hälfte des AdS-Raums, hat aber eine besonders einfache Form für das Linienelement. Es sei $ \mathbf {X} _{\left(d-2\right)}=\left\{X^{1},...,X^{d-2}\right\} $. Die Einbettung einer Hälfte des $ d $-dimensionalen AdS-Raums in den $ d+1 $-dimensionalen Raum ist dann mit $ X^{d-1}>0 $ gegeben durch

$ {\begin{aligned}\mathbf {x} &={\frac {1}{X^{d-1}}}\left\{a\mathbf {X} _{\left(d-2\right)},\;{\frac {1}{2}}\left(\mathbf {X} _{\left(d-2\right)}^{2}+\left(X^{d-1}\right)^{2}-\left(X^{d}\right)^{2}-a^{2}\right)\right\},\\u&=aX^{d}/X^{d-1},\\v&={\frac {1}{2X^{d-1}}}\left(\mathbf {X} _{\left(d-2\right)}^{2}+\left(X^{d-1}\right)^{2}-\left(X^{d}\right)^{2}+a^{2}\right).\end{aligned}} $

Das Linienelement

$ d\tau ^{2}={\frac {a^{2}}{\left(X^{d-1}\right)^{2}}}\left(\left(dX^{d}\right)^{2}-d\mathbf {X} _{\left(d-1\right)}^{2}\right) $

ist konform äquivalent zum Minkowski-Linienelement. Für konstante Zeitvariable $ X^{d} $ handelt es sich um einen hyperbolischen Raum, beschrieben durch Poincaré-Halbraum-Koordinaten.

Die besonderen physikalischen Eigenschaften

Wenn man irgendwo frei in einem solchen Raum schwebt, hat man den Eindruck, sich am Boden eines Gravitationspotentials aufzuhalten: jedes Objekt, das man fortschleudert, kehrt wie ein Bumerang zurück. Noch überraschender ist, dass die Zeit bis zur Rückkehr nicht von der Wucht des Wurfs abhängt: das Objekt entfernt sich auf seiner Rundreise zwar desto weiter, je mehr Schwung man ihm gibt, aber die Rückkehrzeit bleibt stets dieselbe. Wenn man einen Lichtblitz aussendet, der aus Photonen mit der maximal möglichen Geschwindigkeit besteht, so entfernt er sich unendlich weit und kehrt dennoch in endlicher Zeit wieder zurück. Der Grund für dieses seltsame Phänomen ist eine Art Zeitkontraktion, die mit der Entfernung vom Beobachter zunimmt.^[1]

Der Anti-de-Sitter-Raum und die holografische Theorie

Wenn wir den hyperbolischen Raum durch gestapelte Scheiben approximieren, dann gleicht die Anti-de-Sitter-Raumzeit einem Stapel dieser Scheiben, die einen Zylinder bilden. Längs der Zylinderachse vergeht die Zeit.

Am einfachsten ist, sich die Scheiben zunächst als zweidimensional und ihren Rand als Kreislinie vorzustellen. Ein hyperbolischer Raum kann jedoch mehr als zwei Dimensionen haben. Der Anti-de-Sitter-Raum, der unserer Raumzeit mit ihren drei räumlichen Dimensionen am meisten ähnelt, erzeugt eine dreidimensionale Projektion dieser „Scheiben“ als Querschnitt des vierdimensionalen Zylinders.

Im vierdimensionalen Anti-de-Sitter-Raum ist die Grenze des Raums – bezogen auf das Universum – zu jedem Zeitpunkt eine sehr große Kugeloberfläche. Auf dieser Grenze liegt das Hologramm der holografischen Theorie. Dies entspricht der Idee, dass eine Quantengravitationstheorie im Inneren eines solchen Raumes äquivalent zu einer gewöhnlichen Quantenfeldtheorie von Punktteilchen ist, die auf dem Rand gilt. Wenn dies zutrifft, kann man eine relativ gut beherrschbare „Quantenteilchentheorie“ nutzen, um eine hypothetische Quantengravitationstheorie zu definieren, über die wir praktisch nichts wissen.

Siehe auch

• De-Sitter-Raum
• De-Sitter-Modell

Literatur

• Ugo Moschella: The de Sitter and anti-de Sitter Sightseeing Tour. In: Thibault Damour (Hrsg.): Einstein, 1905–2005 - Poincaré Seminar 2005. Birkhäuser, Basel 2005, ISBN 978-3-7643-7435-8, S. 120–134.
• Birgit Jovanović: Masses of anti-de Sitter spacetimes. Dipl.-Arb., Techn. Univ. Wien, 2008 (PDF, abgefragt 17. Februar 2009; 477 kB)
• Carlos Barceló, Matt Visser: Living on the edge: cosmology on the boundary of anti-de Sitter space. In: Physics Letters B. Vol. 482, Issue 1–3, 1. Juni 2000, S. 183–194, DOI:10.1016/S0370-2693(00)00520-7, arxiv:hep-th/0004056.

Einzelnachweis