Eintrittspupille: Unterschied zwischen den Versionen
- Wikipedia:Redundanz Juli 2021
- Geometrische Optik
imported>KaiKemmann |
imported>Olivenmus (Parameter zur betreffenden Redundanzdiskussion ergänzt) |
||
| Zeile 1: | Zeile 1: | ||
{{Redundanztext|3=Eintrittspupille|4=Austrittspupille|2=Juli 2021}} | |||
{{Redundanztext | |||
|3= | |||
|4 | |||
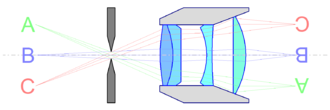
Die '''Eintrittspupille''' ist eine reelle oder virtuelle Öffnung, welche die in ein [[optisches System]] einfallenden Strahlenbündel begrenzt. | Die '''Eintrittspupille''' ist eine reelle oder virtuelle Öffnung, welche die in ein [[optisches System]] einfallenden Strahlenbündel begrenzt. | ||
Sie ist mit der [[Aperturblende]] identisch, falls sich diese in Lichtrichtung vor den [[Optische Abbildung|abbildenden]] Elementen ([[Linse (Optik)|Linsen]] oder Spiegeln) befindet. Anderenfalls entsteht die Eintrittspupille als Bild der Aperturblende, indem diese von den vor ihr liegenden Elementen in den [[Objektraum]] abgebildet wird. | Sie ist mit der [[Blende (Optik)#Aperturblende|Aperturblende]] identisch, falls sich diese in Lichtrichtung vor den [[Optische Abbildung|abbildenden]] Elementen ([[Linse (Optik)|Linsen]] oder Spiegeln) befindet. Anderenfalls entsteht die Eintrittspupille als Bild der Aperturblende, indem diese von den vor ihr liegenden Elementen in den [[Objektraum]] abgebildet wird. | ||
== Bedeutung des Durchmessers der Eintrittspupille == | == Bedeutung des Durchmessers der Eintrittspupille == | ||
Der Durchmesser der Eintrittspupille ist eine Kenngröße der an der optischen Abbildung beteiligten Lichtbündel und somit eine Kenngröße für die übertragene [[Leuchtdichte]]. Je nach | Bei unendlich weit entferntem Objekt ist der Durchmesser des davon ausgehenden achsparallelen Strahlenbündels gleich dem Durchmesser der EP. Der Durchmesser der Eintrittspupille (EP) ist eine Kenngröße der an der optischen Abbildung beteiligten Lichtbündel und somit eine Kenngröße für die übertragene [[Leuchtdichte]]. Je nach Art des optischen Systems wird der Durchmesser der EP unterschiedlich verrechnet. | ||
=== | === Afokales System === | ||
[[Afokales Linsensystem|Afokale]] Systeme wie z. B. [[Fernrohr]]e haben keine Brennweite bzw. diese ist unendlich. Hier wird der EP-Durchmesser meist direkt als Kenngröße angegeben. | |||
=== | === Objektiv für große Objektentfernung === | ||
Hier gibt man in der Regel die Blendenzahl ''k'' an, also den Quotienten aus bildseitiger [[Brennweite]] und EP-Durchmesser. Die [[Lichtstärke (Fotografie)|Lichtstärke]] von Fotoobjektiven ist der Quotient aus größtem einstellbarem EP-Durchmesser und Brennweite. | |||
=== Objektlage nah === | === Objektlage nah === | ||
Bei [[Mikroskop]]en oder allgemein bei optischen Systemen, bei denen die Objektdistanz sehr gering ist, bestimmt der Durchmesser der | Bei [[Mikroskop]]en oder allgemein bei optischen Systemen, bei denen die Objektdistanz sehr gering ist, bestimmt der Durchmesser der EP zusammen mit der Objektdistanz über eine Winkelfunktion den Öffnungswinkel und damit die [[numerische Apertur]]. | ||
== Bedeutung der Position der Eintrittspupille == | == Bedeutung der Position der Eintrittspupille == | ||
Aufgrund der Position der | |||
Aufgrund der Position der EP unterscheidet man drei Perspektiven oder auch Strahlengänge: | |||
=== Die entozentrische Perspektive === | === Die entozentrische Perspektive === | ||
Dies ist, was gemeinhin unter perspektivischer Abbildung verstanden wird. Sie liegt beim menschlichen [[Auge]], bei fotografischen Objektiven sowie vielen anderen optischen Geräten vor. | Dies ist, was gemeinhin unter perspektivischer Abbildung verstanden wird. Sie liegt beim menschlichen [[Auge]], bei fotografischen Objektiven sowie vielen anderen optischen Geräten vor. Sie zeichnet sich dadurch aus, dass weit entfernte Objekte in der Bildebene kleiner abgebildet werden als nähere, gleich große Objekte. | ||
Sie entsteht, wenn sich die EP in Abbildungsrichtung hinter den abzubildenden Objekten befindet, also näher an der Kamera ist (in der Regel liegt sie innerhalb des Objektivs). (Man beachte, dass Abbildungsrichtung und "Blickrichtung" gegenläufig sind.) | |||
Sie entsteht, wenn sich die | |||
=== Die telezentrische Perspektive === | === Die telezentrische Perspektive === | ||
| Zeile 45: | Zeile 36: | ||
[[Datei:Telezentrische.Abbildung.objektseitig.png|miniatur|Objektseitiger telezentrischer Strahlengang]] | [[Datei:Telezentrische.Abbildung.objektseitig.png|miniatur|Objektseitiger telezentrischer Strahlengang]] | ||
'''Beim telezentrischen Strahlengang im Objektraum''' werden gleich große, hintereinanderliegende Objekte in der Bildebene mit dem gleichen Abbildungsmaßstab (d. h. gleich groß) abgebildet. | '''Beim telezentrischen Strahlengang im Objektraum''' werden gleich große, hintereinanderliegende Objekte in der Bildebene mit dem gleichen Abbildungsmaßstab (d. h. gleich groß) abgebildet. Dieser Strahlengang entsteht, wenn die EP im objektseitigen Unendlichen liegt. Die Aperturblende muss entweder innerhalb des Systems und in der [[Fokus|Brennebene]] des davor befindlichen Teilsystems liegen, oder in der Brennebene des Gesamtsystems und damit hinter dem System. | ||
Dies findet zum Beispiel bei Messobjektiven (Messmikroskope) Anwendung, bei denen die Abmessungen von Objekten in unterschiedlichen Objektdistanzen verglichen werden sollen. | Dies findet zum Beispiel bei Messobjektiven (Messmikroskope) Anwendung, bei denen die Abmessungen von Objekten in unterschiedlichen Objektdistanzen verglichen werden sollen. | ||
[[Datei:Telezentrische.Abbildung.bildseitig.png|miniatur|Bildseitiger telezentrischer Strahlengang]] | [[Datei:Telezentrische.Abbildung.bildseitig.png|miniatur|Bildseitiger telezentrischer Strahlengang]] | ||
| Zeile 57: | Zeile 46: | ||
Dieses findet zum Beispiel bei großformatigen Projektionen ([[Autokino]]) Anwendung, bei denen eine zur optischen Achse parallele Bewegung der Bildebene (Leinwand) zu störenden, lokalen Größenänderungen des Bildes führen würde. | Dieses findet zum Beispiel bei großformatigen Projektionen ([[Autokino]]) Anwendung, bei denen eine zur optischen Achse parallele Bewegung der Bildebene (Leinwand) zu störenden, lokalen Größenänderungen des Bildes führen würde. | ||
Dieser Strahlengang entsteht, wenn sich die | Dieser Strahlengang entsteht, wenn sich die Aperturblende im objektseitigen [[Fokus|Brennpunkt]] befindet, und somit mit der Eintrittspupille identisch ist. In diesem Fall liegt die [[Austrittspupille]] im bildseitigen Unendlichen. | ||
=== Die | === Die [[Liste griechischer Präfixe|peri-/hyper]]zentrische Perspektive === | ||
Bei dieser Darstellung werden weiter entfernte | Bei dieser Darstellung werden weiter entfernte Objekte in der Bildebene größer dargestellt als nähere, gleich große. | ||
Sie entsteht, wenn die | Sie entsteht, wenn die EP in Abbildungsrichtung vor den Objekten liegt, also weiter als diese von der Kamera entfernt ist. | ||
In der [[Bildverarbeitung]] werden hyperzentrische Objektive verwendet, um die Mantelflächen zylinderförmiger Objekte (Tablettendosen, Gewinde | In der [[Bildverarbeitung]] werden hyperzentrische Objektive verwendet, um die Mantelflächen zylinderförmiger Objekte (Tablettendosen, Gewinde etc.) von der Stirnseite des Zylinders aus zu betrachten. | ||
Dabei befindet sich die Objektachse im Idealfall auf der optischen Achse des Objektivs. Kreise mit Objektradius und Mittelpunkt auf der Zylinderachse werden in diesem Fall in [[Konzentrizität|konzentrische Kreise]] abgebildet und Schraubengewinde werden auf eine Spirale abgebildet. | Dabei befindet sich die Objektachse im Idealfall auf der optischen Achse des Objektivs. Kreise mit Objektradius und Mittelpunkt auf der Zylinderachse werden in diesem Fall in [[Konzentrizität|konzentrische Kreise]] abgebildet und Schraubengewinde werden auf eine Spirale abgebildet. | ||
Die Frontlinsen hyperzentrische Objektive müssen | Die Frontlinsen hyperzentrische Objektive müssen größer als die betrachteten Objekte sein. | ||
''Siehe auch:'' [[Blende (Optik)]], [[Austrittspupille]], [[Telezentrisches Objektiv]] | ''Siehe auch:'' [[Blende (Optik)]], [[Austrittspupille]], [[Telezentrisches Objektiv]] | ||
| Zeile 74: | Zeile 63: | ||
=== Panoramafotografie === | === Panoramafotografie === | ||
Die Kenntnis der Lage der Eintrittspupille ist wichtig für die Erstellung von [[Panoramabild|Panoramen]] aus mehreren Einzelbildern. Nur wenn die Kamera zwischen der Aufnahme verschiedener, sich überlappender Teilbilder um die Eintrittspupille als Drehpunkt geschwenkt wird, können diese später am Computer | Die Kenntnis der Lage der Eintrittspupille ist wichtig für die Erstellung von [[Panoramabild|Panoramen]] aus mehreren Einzelbildern. Nur wenn die Kamera zwischen der Aufnahme verschiedener, sich überlappender Teilbilder um die Eintrittspupille als Drehpunkt geschwenkt wird, können diese später am Computer bei der [[Bildbearbeitung]] ohne Parallaxenfehler zu einem Panoramabild zusammengesetzt werden.<ref>[http://www.janrik.net/PanoPostings/NoParallaxPoint/TheoryOfTheNoParallaxPoint.pdf Littlefield: Theory of the "No-Parallax" Point in Panorama Photography]</ref> Im Englischen wird dieser spezielle Drehpunkt auch als „No-Parallax-Point“ bezeichnet, weil es der Punkt ist, bei dem der [[Parallaxenfehler]] vermieden wird.<ref>[https://pt4pano.com/blog/2010/nodalpunkt-npp-oder-lpp Nodalpunkt, NPP oder LPP?] Blogbeitrag von E.Hopf auf pt4pano.com, abgerufen am 29. September 2021</ref> | ||
Bei ausschließlich sehr weit oder gleich weit entfernten | Bei ausschließlich sehr weit oder gleich weit entfernten Objekten fällt es nicht unbedingt ins Gewicht, wenn um einen vom Eintrittspupillenzentrum abweichenden Punkt – z. B. um das Bildzentrum oder einen der beiden [[Nodalpunkte]] − verschwenkt wird, bei der gleichzeitigen Abbildung von weit entfernten und in der Nähe befindlichen Objekten hingegen schon. Dies kann sich später beim Zusammensetzen der Bilder in Form von so genannten ''Geisterbildern'' bemerkbar machen. | ||
==== Nodalpunktadapter ==== | ==== Nodalpunktadapter ==== | ||
Da die Eintrittspupille bei den meisten Kameras nicht über dem Stativgewinde liegt, sind für präzise | Da die Eintrittspupille bei den meisten Kameras nicht über dem Stativgewinde liegt, sind für präzise Panoramaaufnahmen spezielle (und oft teure) [[Einstellschlitten]] bzw. ''Nodalpunkt-[[Adapter]]'' erforderlich, die zwischen [[Stativ]] und Kamera angebracht werden. Sie erlauben es, ein Objektiv mitsamt der Kamera um einen frei wählbaren Drehpunkt (innerhalb der mechanischen Grenzen des Adapters) zu verschwenken. Im Gegensatz dazu stehen einfache Drehteller oder Teilscheiben, die durch eine gleichmäßige Gradaufteilung beim Schwenken gleichmäßige Aufnahmen ermöglichen, aber keine freie Wahl des Drehpunkts erlauben. | ||
Neben der Drehung um die Eintrittspupille erlauben Nodalpunktadapter auch die Wahl eines anderen Drehpunktes – natürlich auch | Neben der Drehung um die Eintrittspupille erlauben Nodalpunktadapter auch die Wahl eines anderen Drehpunktes – natürlich auch einen der beiden [[Nodalpunkte]]. Die Bezeichnung ''Nodalpunkt-Adapter'' rührt möglicherweise daher, dass der Begriff Nodalpunkt früher fälschlicherweise für das Zentrum der Eintrittspupille verwendet wurde. Im Zusammenhang mit Panoramafotografie haben die Nodalpunkte jedenfalls keine Bedeutung. | ||
== Siehe auch == | == Siehe auch == | ||
* [[ | * [[Blendenzahl]] | ||
* [[Blende (Optik)]] | * [[Blende (Optik)]] | ||
* [[Kritische Blende]] | * [[Kritische Blende]] | ||
== Einzelnachweise == | |||
<references /> | |||
[[Kategorie:Geometrische Optik]] | [[Kategorie:Geometrische Optik]] | ||
Aktuelle Version vom 6. Januar 2022, 20:47 Uhr
Die Eintrittspupille ist eine reelle oder virtuelle Öffnung, welche die in ein optisches System einfallenden Strahlenbündel begrenzt.
Sie ist mit der Aperturblende identisch, falls sich diese in Lichtrichtung vor den abbildenden Elementen (Linsen oder Spiegeln) befindet. Anderenfalls entsteht die Eintrittspupille als Bild der Aperturblende, indem diese von den vor ihr liegenden Elementen in den Objektraum abgebildet wird.
Bedeutung des Durchmessers der Eintrittspupille
Bei unendlich weit entferntem Objekt ist der Durchmesser des davon ausgehenden achsparallelen Strahlenbündels gleich dem Durchmesser der EP. Der Durchmesser der Eintrittspupille (EP) ist eine Kenngröße der an der optischen Abbildung beteiligten Lichtbündel und somit eine Kenngröße für die übertragene Leuchtdichte. Je nach Art des optischen Systems wird der Durchmesser der EP unterschiedlich verrechnet.
Afokales System
Afokale Systeme wie z. B. Fernrohre haben keine Brennweite bzw. diese ist unendlich. Hier wird der EP-Durchmesser meist direkt als Kenngröße angegeben.
Objektiv für große Objektentfernung
Hier gibt man in der Regel die Blendenzahl k an, also den Quotienten aus bildseitiger Brennweite und EP-Durchmesser. Die Lichtstärke von Fotoobjektiven ist der Quotient aus größtem einstellbarem EP-Durchmesser und Brennweite.
Objektlage nah
Bei Mikroskopen oder allgemein bei optischen Systemen, bei denen die Objektdistanz sehr gering ist, bestimmt der Durchmesser der EP zusammen mit der Objektdistanz über eine Winkelfunktion den Öffnungswinkel und damit die numerische Apertur.
Bedeutung der Position der Eintrittspupille
Aufgrund der Position der EP unterscheidet man drei Perspektiven oder auch Strahlengänge:
Die entozentrische Perspektive
Dies ist, was gemeinhin unter perspektivischer Abbildung verstanden wird. Sie liegt beim menschlichen Auge, bei fotografischen Objektiven sowie vielen anderen optischen Geräten vor. Sie zeichnet sich dadurch aus, dass weit entfernte Objekte in der Bildebene kleiner abgebildet werden als nähere, gleich große Objekte.
Sie entsteht, wenn sich die EP in Abbildungsrichtung hinter den abzubildenden Objekten befindet, also näher an der Kamera ist (in der Regel liegt sie innerhalb des Objektivs). (Man beachte, dass Abbildungsrichtung und "Blickrichtung" gegenläufig sind.)
Die telezentrische Perspektive
Bei der telezentrischen Perspektive unterscheidet man den telezentrischen Strahlengang im Objekt- und im Bildraum.
Beim telezentrischen Strahlengang im Objektraum werden gleich große, hintereinanderliegende Objekte in der Bildebene mit dem gleichen Abbildungsmaßstab (d. h. gleich groß) abgebildet. Dieser Strahlengang entsteht, wenn die EP im objektseitigen Unendlichen liegt. Die Aperturblende muss entweder innerhalb des Systems und in der Brennebene des davor befindlichen Teilsystems liegen, oder in der Brennebene des Gesamtsystems und damit hinter dem System.
Dies findet zum Beispiel bei Messobjektiven (Messmikroskope) Anwendung, bei denen die Abmessungen von Objekten in unterschiedlichen Objektdistanzen verglichen werden sollen.
Der telezentrische Strahlengang im Bildraum ist das seitenvertauschte Gegenstück zum telezentrischen Strahlengang im Objektraum, das heißt, ein Objekt wird in unterschiedlichen Bildebenen gleich groß abgebildet.
Dieses findet zum Beispiel bei großformatigen Projektionen (Autokino) Anwendung, bei denen eine zur optischen Achse parallele Bewegung der Bildebene (Leinwand) zu störenden, lokalen Größenänderungen des Bildes führen würde.
Dieser Strahlengang entsteht, wenn sich die Aperturblende im objektseitigen Brennpunkt befindet, und somit mit der Eintrittspupille identisch ist. In diesem Fall liegt die Austrittspupille im bildseitigen Unendlichen.
Die peri-/hyperzentrische Perspektive
Bei dieser Darstellung werden weiter entfernte Objekte in der Bildebene größer dargestellt als nähere, gleich große. Sie entsteht, wenn die EP in Abbildungsrichtung vor den Objekten liegt, also weiter als diese von der Kamera entfernt ist.
In der Bildverarbeitung werden hyperzentrische Objektive verwendet, um die Mantelflächen zylinderförmiger Objekte (Tablettendosen, Gewinde etc.) von der Stirnseite des Zylinders aus zu betrachten.
Dabei befindet sich die Objektachse im Idealfall auf der optischen Achse des Objektivs. Kreise mit Objektradius und Mittelpunkt auf der Zylinderachse werden in diesem Fall in konzentrische Kreise abgebildet und Schraubengewinde werden auf eine Spirale abgebildet.
Die Frontlinsen hyperzentrische Objektive müssen größer als die betrachteten Objekte sein.
Siehe auch: Blende (Optik), Austrittspupille, Telezentrisches Objektiv
Panoramafotografie
Die Kenntnis der Lage der Eintrittspupille ist wichtig für die Erstellung von Panoramen aus mehreren Einzelbildern. Nur wenn die Kamera zwischen der Aufnahme verschiedener, sich überlappender Teilbilder um die Eintrittspupille als Drehpunkt geschwenkt wird, können diese später am Computer bei der Bildbearbeitung ohne Parallaxenfehler zu einem Panoramabild zusammengesetzt werden.[1] Im Englischen wird dieser spezielle Drehpunkt auch als „No-Parallax-Point“ bezeichnet, weil es der Punkt ist, bei dem der Parallaxenfehler vermieden wird.[2]
Bei ausschließlich sehr weit oder gleich weit entfernten Objekten fällt es nicht unbedingt ins Gewicht, wenn um einen vom Eintrittspupillenzentrum abweichenden Punkt – z. B. um das Bildzentrum oder einen der beiden Nodalpunkte − verschwenkt wird, bei der gleichzeitigen Abbildung von weit entfernten und in der Nähe befindlichen Objekten hingegen schon. Dies kann sich später beim Zusammensetzen der Bilder in Form von so genannten Geisterbildern bemerkbar machen.
Nodalpunktadapter
Da die Eintrittspupille bei den meisten Kameras nicht über dem Stativgewinde liegt, sind für präzise Panoramaaufnahmen spezielle (und oft teure) Einstellschlitten bzw. Nodalpunkt-Adapter erforderlich, die zwischen Stativ und Kamera angebracht werden. Sie erlauben es, ein Objektiv mitsamt der Kamera um einen frei wählbaren Drehpunkt (innerhalb der mechanischen Grenzen des Adapters) zu verschwenken. Im Gegensatz dazu stehen einfache Drehteller oder Teilscheiben, die durch eine gleichmäßige Gradaufteilung beim Schwenken gleichmäßige Aufnahmen ermöglichen, aber keine freie Wahl des Drehpunkts erlauben.
Neben der Drehung um die Eintrittspupille erlauben Nodalpunktadapter auch die Wahl eines anderen Drehpunktes – natürlich auch einen der beiden Nodalpunkte. Die Bezeichnung Nodalpunkt-Adapter rührt möglicherweise daher, dass der Begriff Nodalpunkt früher fälschlicherweise für das Zentrum der Eintrittspupille verwendet wurde. Im Zusammenhang mit Panoramafotografie haben die Nodalpunkte jedenfalls keine Bedeutung.
Siehe auch
- Blendenzahl
- Blende (Optik)
- Kritische Blende
Einzelnachweise
- ↑ Littlefield: Theory of the "No-Parallax" Point in Panorama Photography
- ↑ Nodalpunkt, NPP oder LPP? Blogbeitrag von E.Hopf auf pt4pano.com, abgerufen am 29. September 2021