Multipendel: Unterschied zwischen den Versionen
imported>Debenben K (HC: Entferne Kategorie:Dynamisches System (Physik); Ergänze Kategorie:Dynamisches System) |
143.50.47.158 (Diskussion) |
||
| Zeile 47: | Zeile 47: | ||
<math>V(\varphi_1,...,\varphi_n) = g \sum_{k=1}^{n} m_k y_k</math> | <math>V(\varphi_1,...,\varphi_n) = g \sum_{k=1}^{n} m_k y_k</math> | ||
Somit ist die Lagrange Funktion <math>L=T-V</math>: | Somit ist die Lagrange-Funktion <math>L=T-V</math>: | ||
<math>L(\varphi_1,...,\varphi_n,\dot{\varphi}_1,...,\dot{\varphi}_n) = \frac{1}{2} \sum_{k=1}^{n} m_k \left[\left(\sum_{i=1}^{k} l_i \dot{\varphi}_i \cos\varphi_i\right)^2+\left(\sum_{i=1}^{k} l_i \dot{\varphi}_i \sin\varphi_i\right)^2\right] + g \sum_{k=1}^{n} \sum_{i=1}^{k} m_k l_i \cos\varphi_i</math> | <math>L(\varphi_1,...,\varphi_n,\dot{\varphi}_1,...,\dot{\varphi}_n) = \frac{1}{2} \sum_{k=1}^{n} m_k \left[\left(\sum_{i=1}^{k} l_i \dot{\varphi}_i \cos\varphi_i\right)^2+\left(\sum_{i=1}^{k} l_i \dot{\varphi}_i \sin\varphi_i\right)^2\right] + g \sum_{k=1}^{n} \sum_{i=1}^{k} m_k l_i \cos\varphi_i</math> | ||
| Zeile 65: | Zeile 65: | ||
Die Bewegungsgleichungen für die [[generalisierte Koordinate|generalisierten Koordinaten]] (<math>{\varphi_{1}},...,{\varphi_{n}}</math>) stellen ein nichtlineares System von <math>n</math> [[Differentialgleichungen]] zweiter Ordnung dar, welches für <math>n>1</math> analytisch nicht lösbar ist. | Die Bewegungsgleichungen für die [[generalisierte Koordinate|generalisierten Koordinaten]] (<math>{\varphi_{1}},...,{\varphi_{n}}</math>) stellen ein nichtlineares System von <math>n</math> [[Differentialgleichungen]] zweiter Ordnung dar, welches für <math>n>1</math> analytisch nicht lösbar ist. | ||
Es kann bei <math>2n</math> bekannten Nebenbedingungen, beispielsweise | Es kann bei <math>2n</math> bekannten Nebenbedingungen, beispielsweise den [[Anfangswertproblem|Startwerten]] | ||
<math>\left( \varphi_1(t=0),...,\varphi_n(t=0),\dot{\varphi}_1(t=0),...,\dot{\varphi}_n(t=0) \right)</math> | <math>\left( \varphi_1(t=0),...,\varphi_n(t=0),\dot{\varphi}_1(t=0),...,\dot{\varphi}_n(t=0) \right),</math> | ||
mittels [[ | mittels [[Liste numerischer Verfahren#Numerik gewöhnlicher Differentialgleichungen|numerischer Verfahren]] gelöst werden. Zwecks Vereinfachung der Bewegungsgleichungen können [[Kleinwinkelnäherung]]en vorgenommen werden. | ||
Für Stufen <math>n>1</math> entstehen chaotische Bewegungsmuster. Hier führen bereits geringfügige Änderungen der lokalen Koordinaten | Für Stufen <math>n>1</math> entstehen chaotische Bewegungsmuster. Hier führen bereits geringfügige Änderungen der lokalen Koordinaten oder ihrer zeitlichen Ableitungen zu deutlichen Änderungen im weiteren Bewegungsablauf. | ||
== Bewegungsgleichungen für ein- bis dreistufige Pendel == | == Bewegungsgleichungen für ein- bis dreistufige Pendel == | ||
| Zeile 127: | Zeile 127: | ||
Ein Beispiel für ein Doppelpendel ist eine [[Glocke]] mit Klöppel. | Ein Beispiel für ein Doppelpendel ist eine [[Glocke]] mit Klöppel. | ||
=== | === Tripelpendel === | ||
Der Fall <math>n=3</math> stellt das ''' | Der Fall <math>n=3</math> stellt das '''Tripelpendel''' dar. | ||
Hier ergibt sich die kinetische Energie <math>T</math> zu: | Hier ergibt sich die kinetische Energie <math>T</math> zu: | ||
| Zeile 157: | Zeile 157: | ||
<math>l_{3}\ddot{\varphi}_{3} + l_{2}\ddot{\varphi}_{2} \cos(\varphi_{2}-\varphi_{3}) + l_{1}\ddot{\varphi}_{1} \cos(\varphi_{1}-\varphi_{3}) - l_2 \dot{\varphi}_{2}^2 \sin(\varphi_{2}-\varphi_{3}) - l_1 \dot{\varphi}_{1}^2 \sin(\varphi_{1}-\varphi_{3}) + g \sin\varphi_3=0</math> | <math>l_{3}\ddot{\varphi}_{3} + l_{2}\ddot{\varphi}_{2} \cos(\varphi_{2}-\varphi_{3}) + l_{1}\ddot{\varphi}_{1} \cos(\varphi_{1}-\varphi_{3}) - l_2 \dot{\varphi}_{2}^2 \sin(\varphi_{2}-\varphi_{3}) - l_1 \dot{\varphi}_{1}^2 \sin(\varphi_{1}-\varphi_{3}) + g \sin\varphi_3=0</math> | ||
=== Simulation der [[ | === Simulation der [[Trajektorie (Physik)|Trajektorien]] === | ||
<gallery> | <gallery> | ||
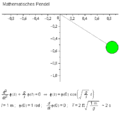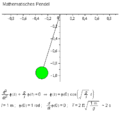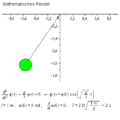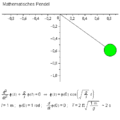
Mathematisches pendel.gif|Simulation: <math>n=1</math> | |||
Mathematisches doppelpendel.gif|Simulation: <math>n=2</math> | |||
Mathematisches dreifachpendel.gif|Simulation: <math>n=3</math> | |||
</gallery> | </gallery> | ||
== Literatur == | == Literatur == | ||
*Georg Hamel: ''Theoretische Mechanik''. Springer, Berlin 1967. Berichtiger Reprint 1978, ISBN 3-540-03816-7 | * Georg Hamel: ''Theoretische Mechanik''. Springer, Berlin 1967. Berichtiger Reprint 1978, ISBN 3-540-03816-7 | ||
*Friedhelm Kuypers: ''Klassische Mechanik''. 5. Auflage. VCH, Weinheim 1997, ISBN 3-527-29269-1 | * Friedhelm Kuypers: ''Klassische Mechanik''. 5. Auflage. VCH, Weinheim 1997, ISBN 3-527-29269-1 | ||
*Landau / | * Landau / Lifschitz: ''Lehrbuch der theoretischen Physik. Band 1: Mechanik''. 14. Auflage. Deutsch, Thun 1997, ISBN 3-8171-1326-9 | ||
== Weblinks == | |||
* [http://blog.tinowagner.com/2008/04/02/doppelpendel/ Doppelpendel-Simulation in Java und Python] | |||
== Quellen == | == Quellen == | ||
*L. D. Landau, E. M. Lifschitz: ''Volume 1 of Course of Theoretical Physics''. 3rd Edition 1976, ISBN 0-7506-2896-0, §5, S. 11 f. ( | * L. D. Landau, E. M. Lifschitz: ''Volume 1 of Course of Theoretical Physics''. 3rd Edition 1976, ISBN 0-7506-2896-0, §5, S. 11 f. (englisch) | ||
*[http://scienceworld.wolfram.com/physics/DoublePendulum.html Herleitung der Differentialgleichungen zur Beschreibung des Doppelpendels | * [http://scienceworld.wolfram.com/physics/DoublePendulum.html Herleitung der Differentialgleichungen zur Beschreibung des Doppelpendels] (englisch) | ||
[[Kategorie:Pendel]] | [[Kategorie:Pendel]] | ||
[[Kategorie:Nichtlineare Dynamik]] | [[Kategorie:Nichtlineare Dynamik]] | ||
Aktuelle Version vom 24. Juni 2021, 14:24 Uhr
Ein Multipendel ist ein Pendel, an dessen Arm weitere Pendel gehängt sind. Es entsteht ein unvorhersehbares Bewegungsmuster, welches bereits bei geringfügigen Störungen stark variiert. Es lassen sich chaotische Prozesse leicht simulieren, weshalb es sich zu einem beliebten Modell in der Chaostheorie entwickelt hat.
Modellvorstellung
Das Modell des Multipendels $ n $-ter Stufe ist ein idealisiertes System eines Fadenpendels, an dessen schwingendem Massenpunkt $ n-1 $ weitere baugleiche Fadenpendel gekoppelt sind. Die verbindenden Fäden zwischen Aufhängepunkt und den Massenpunkten werden als vollkommen unelastische, massenlose Stäbe betrachtet. Das gesamte System wird als reibungsfrei aufgefasst.
Bewegungsgleichungen des Multipendels n-ter Stufe
Die Bewegungsgleichungen für ein Multipendel $ n $-ter Stufe lassen sich mit dem Lagrange-Formalismus zweiter Art herleiten.
Generalisierte Koordinaten
Mittels Trigonometrie erhält man:
$ x_{1}=l_{1}\sin \varphi _{1} $
$ y_{1}=-l_{1}\cos \varphi _{1} $
$ x_{2}=l_{1}\sin \varphi _{1}+l_{2}\sin \varphi _{2} $
$ y_{2}=-l_{1}\cos \varphi _{1}-l_{2}\cos \varphi _{2} $
...
$ x_{n}=l_{1}\sin \varphi _{1}+...+l_{n}\sin \varphi _{n} $
$ y_{n}=-l_{1}\cos \varphi _{1}-...-l_{n}\cos \varphi _{n} $
Folglich können die kartesischen Koordinaten $ (x_{k}|y_{k}) $ der Massenpunkte $ m_{k} $ für $ k $ ∈ {1,...,$ n $} und ihre zeitlichen Ableitungen in folgender Form geschrieben werden:
$ x_{k}=\sum _{i=1}^{k}l_{i}\sin \varphi _{i} $
$ {\dot {x}}_{k}=\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\cos \varphi _{i} $
$ y_{k}=-\sum _{i=1}^{k}l_{i}\cos \varphi _{i} $
$ {\dot {y}}_{k}=\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\sin \varphi _{i} $
Lagrange-Funktion
Kinetische Energie $ T $ und Potential $ V $ ergeben:
$ T(\varphi _{1},...,\varphi _{n},{\dot {\varphi }}_{1},...,{\dot {\varphi }}_{n})=\sum _{k=1}^{n}{\frac {m_{k}}{2}}({\dot {x}}_{k}^{2}+{\dot {y}}_{k}^{2}) $
$ V(\varphi _{1},...,\varphi _{n})=g\sum _{k=1}^{n}m_{k}y_{k} $
Somit ist die Lagrange-Funktion $ L=T-V $:
$ L(\varphi _{1},...,\varphi _{n},{\dot {\varphi }}_{1},...,{\dot {\varphi }}_{n})={\frac {1}{2}}\sum _{k=1}^{n}m_{k}\left[\left(\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\cos \varphi _{i}\right)^{2}+\left(\sum _{i=1}^{k}l_{i}{\dot {\varphi }}_{i}\sin \varphi _{i}\right)^{2}\right]+g\sum _{k=1}^{n}\sum _{i=1}^{k}m_{k}l_{i}\cos \varphi _{i} $
Bewegungsgleichungen
Die Bewegungsgleichungen des Multipendels n-ter Stufe ergeben sich aus
$ {d \over dt}{\partial {L} \over \partial {{\dot {\varphi }}_{j}}}-{\partial {L} \over \partial {\varphi _{j}}}=0 $
bzw.
$ {d \over dt}{\partial {T} \over \partial {{\dot {\varphi }}_{j}}}-{\partial {} \over \partial {\varphi _{j}}}(T-V)=0 $
für $ j $ ∈ {1,...,$ n $}.
Die Bewegungsgleichungen für die generalisierten Koordinaten ($ {\varphi _{1}},...,{\varphi _{n}} $) stellen ein nichtlineares System von $ n $ Differentialgleichungen zweiter Ordnung dar, welches für $ n>1 $ analytisch nicht lösbar ist.
Es kann bei $ 2n $ bekannten Nebenbedingungen, beispielsweise den Startwerten
$ \left(\varphi _{1}(t=0),...,\varphi _{n}(t=0),{\dot {\varphi }}_{1}(t=0),...,{\dot {\varphi }}_{n}(t=0)\right), $
mittels numerischer Verfahren gelöst werden. Zwecks Vereinfachung der Bewegungsgleichungen können Kleinwinkelnäherungen vorgenommen werden.
Für Stufen $ n>1 $ entstehen chaotische Bewegungsmuster. Hier führen bereits geringfügige Änderungen der lokalen Koordinaten oder ihrer zeitlichen Ableitungen zu deutlichen Änderungen im weiteren Bewegungsablauf.
Bewegungsgleichungen für ein- bis dreistufige Pendel
Mathematisches Pendel
Für $ n=1 $ ergibt sich der einfache Fall des mathematischen Pendels.
Hier ergeben sich kinetische Energie $ T $ und Potential $ V $ zu
$ T(\varphi ,{\dot {\varphi }})={\frac {m}{2}}l^{2}{\dot {\varphi }}^{2} $
$ V(\varphi )=-mgl\cos \varphi $
mit $ m:=m_{1},l:=l_{1},\varphi :=\varphi _{1} $.
Entsprechend ist die Bewegungsgleichung:
$ {\ddot {\varphi }}+{\frac {g}{l}}\sin \varphi =0 $
Mit der Kleinwinkelnäherung $ \sin \varphi \approx \varphi $ lässt sich die Gleichung vereinfachen:
$ {\ddot {\varphi }}+{\frac {g}{l}}\varphi =0 $
Eine zweckmäßige Lösung der Bewegungsgleichung ist
$ \varphi (t)=\varphi (0)\cos \left({\sqrt {\frac {g}{l}}}t+\alpha \right) $,
sodass bei bekannten Startbedingungen für den Parameter $ \alpha $ gilt:
$ \alpha =\arcsin \left(-{\frac {{\dot {\varphi }}(0)}{\varphi (0)}}{\sqrt {\frac {l}{g}}}\right) $
Das Pendel schwingt entsprechend harmonisch mit der Periode:
$ T=2\pi {\sqrt {\frac {l}{g}}} $
Doppelpendel
Der Fall $ n=2 $ stellt das Doppelpendel dar.
Hier ergeben sich kinetische Energie $ T $ und Potential $ V $ zu:
$ T(\varphi _{1},\varphi _{2},{\dot {\varphi }}_{1},{\dot {\varphi }}_{2})={\frac {m_{1}}{2}}l_{1}^{2}{\dot {\varphi }}_{1}^{2}+{\frac {m_{2}}{2}}\left(l_{1}^{2}{\dot {\varphi }}_{1}^{2}+l_{2}^{2}{\dot {\varphi }}_{2}^{2}+2l_{1}l_{2}{\dot {\varphi }}_{1}{\dot {\varphi }}_{2}\cos(\varphi _{1}-\varphi _{2})\right) $
$ V(\varphi _{1},\varphi _{2})=-(m_{1}+m_{2})gl_{1}\cos \varphi _{1}-m_{2}gl_{2}\cos \varphi _{2} $
Entsprechend sind die Bewegungsgleichungen:
$ m_{2}l_{2}{\ddot {\varphi }}_{2}\cos \left(\varphi _{1}-\varphi _{2}\right)+\left(m_{1}+m_{2}\right)l_{1}{\ddot {\varphi }}_{1}+m_{2}l_{2}{\dot {\varphi }}_{2}^{2}\sin \left(\varphi _{1}-\varphi _{2}\right)+\left(m_{1}+m_{2}\right)g\sin \varphi _{1}=0 $
und
$ l_{2}{\ddot {\varphi }}_{2}+l_{1}{\ddot {\varphi }}_{1}\cos \left(\varphi _{1}-\varphi _{2}\right)-l_{1}{\dot {\varphi }}_{1}^{2}\sin \left(\varphi _{1}-\varphi _{2}\right)+g\sin \varphi _{2}=0 $
Ein Beispiel für ein Doppelpendel ist eine Glocke mit Klöppel.
Tripelpendel
Der Fall $ n=3 $ stellt das Tripelpendel dar.
Hier ergibt sich die kinetische Energie $ T $ zu:
$ T(\varphi _{1},\varphi _{2},\varphi _{3},{\dot {\varphi }}_{1},{\dot {\varphi }}_{2},{\dot {\varphi }}_{3})={\frac {m_{1}+m_{2}+m_{3}}{2}}l_{1}^{2}{\dot {\varphi }}_{1}^{2}+{\frac {m_{2}+m_{3}}{2}}l_{2}^{2}{\dot {\varphi }}_{2}^{2}+{\frac {m_{3}}{2}}l_{3}^{2}{\dot {\varphi }}_{3}^{2}+(m_{2}+m_{3})l_{1}l_{2}{\dot {\varphi }}_{1}{\dot {\varphi }}_{2}\cos(\varphi _{1}-\varphi _{2}) $
$ +m_{3}l_{1}l_{3}{\dot {\varphi }}_{1}{\dot {\varphi }}_{3}\cos(\varphi _{1}-\varphi _{3})+m_{3}l_{2}l_{3}{\dot {\varphi }}_{2}{\dot {\varphi }}_{3}\cos(\varphi _{2}-\varphi _{3}) $
Für das Potential $ V $ gilt:
$ V(\varphi _{1},\varphi _{2},\varphi _{3})=-(m_{1}+m_{2}+m_{3})gl_{1}\cos \varphi _{1}-(m_{2}+m_{3})gl_{2}\cos \varphi _{2}-m_{3}gl_{3}\cos \varphi _{3} $
Entsprechend sind die Bewegungsgleichungen:
$ m_{3}l_{3}{\ddot {\varphi }}_{3}\cos(\varphi _{1}-\varphi _{3})+(m_{2}+m_{3})l_{2}{\ddot {\varphi }}_{2}\cos(\varphi _{1}-\varphi _{2})+(m_{1}+m_{2}+m_{3})l_{1}{\ddot {\varphi }}_{1}+m_{3}l_{3}{\dot {\varphi }}_{3}^{2}\sin(\varphi _{1}-\varphi _{3}) $
$ +(m_{2}+m_{3})l_{2}{\dot {\varphi }}_{2}^{2}\sin(\varphi _{1}-\varphi _{2})+(m_{1}+m_{2}+m_{3})g\sin \varphi _{1}=0 $
und
$ m_{3}l_{3}{\ddot {\varphi }}_{3}\cos(\varphi _{2}-\varphi _{3})+(m_{2}+m_{3})l_{2}{\ddot {\varphi }}_{2}+(m_{2}+m_{3})l_{1}{\ddot {\varphi }}_{1}\cos(\varphi _{1}-\varphi _{2})-(m_{2}+m_{3})l_{1}{\dot {\varphi }}_{1}^{2}\sin(\varphi _{1}-\varphi _{2}) $
$ +m_{3}l_{3}{\dot {\varphi }}_{3}^{2}\sin(\varphi _{2}-\varphi _{3})+(m_{2}+m_{3})g\sin \varphi _{2}=0 $
und
$ l_{3}{\ddot {\varphi }}_{3}+l_{2}{\ddot {\varphi }}_{2}\cos(\varphi _{2}-\varphi _{3})+l_{1}{\ddot {\varphi }}_{1}\cos(\varphi _{1}-\varphi _{3})-l_{2}{\dot {\varphi }}_{2}^{2}\sin(\varphi _{2}-\varphi _{3})-l_{1}{\dot {\varphi }}_{1}^{2}\sin(\varphi _{1}-\varphi _{3})+g\sin \varphi _{3}=0 $
Simulation der Trajektorien
Literatur
- Georg Hamel: Theoretische Mechanik. Springer, Berlin 1967. Berichtiger Reprint 1978, ISBN 3-540-03816-7
- Friedhelm Kuypers: Klassische Mechanik. 5. Auflage. VCH, Weinheim 1997, ISBN 3-527-29269-1
- Landau / Lifschitz: Lehrbuch der theoretischen Physik. Band 1: Mechanik. 14. Auflage. Deutsch, Thun 1997, ISBN 3-8171-1326-9
Weblinks
Quellen
- L. D. Landau, E. M. Lifschitz: Volume 1 of Course of Theoretical Physics. 3rd Edition 1976, ISBN 0-7506-2896-0, §5, S. 11 f. (englisch)
- Herleitung der Differentialgleichungen zur Beschreibung des Doppelpendels (englisch)