Eulersche Winkel: Unterschied zwischen den Versionen
- Wikipedia:Vorlagenfehler/Vorlage:Cite journal/Parameter language fehlt
- Seiten mit Skriptfehlern
- Wikipedia:Wikidata P2812 verschieden
- Analytische Geometrie
- Kristallographie
- Klassische Mechanik
- Winkel
- Leonhard Euler als Namensgeber
80.110.10.10 (Diskussion) (Die Matrix und die transponierte Matrix liegen vertauscht vor) |
imported>Felivik K (Der Satz, dass "jede Bewegung mit einem Fixpunkt eine Drehung um eine Achse ist", gilt nur für eigentliche Bewegungen. Uneigentliche Bewegungen mit einem Fixpunkt sind z.B. Drehspiegelungen.) |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:Euler2a.gif|mini|hochkant=1|Drehung eines Körpers als Folge von drei einzelnen Drehungen um seine Körperachsen z,x',z".<br /> | |||
Eigenes Koordinatensystem: <span style="color:red">rot</span><br /> | |||
festes Referenzsystem:<span style="color:blue">blau</span>]] | |||
Die '''eulerschen Winkel''' (oder '''Euler-Winkel'''), benannt nach dem Schweizer [[Mathematiker]] [[Leonhard Euler]], sind ein Satz von drei [[Winkel]]n, mit denen die Orientierung (Drehlage) eines festen Körpers im dreidimensionalen [[Euklidischer Raum|euklidischen Raum]] beschrieben werden kann.<ref name="goldstein" /> Sie werden üblicherweise mit <math>\alpha, \beta, \gamma</math> oder mit <math>\varphi, \theta, \psi</math> bezeichnet. Der Körper kann zum Beispiel ein Kreisel sein (in der theoretischen Physik) oder ein Fahrzeug, ein Schiff oder ein Flugzeug. In der Astronomie kann der „Körper“ auch die Bahnellipse eines Himmelskörpers sein. | |||
[[ | Anstatt der Drehlage eines Körpers können eulersche Winkel auch die Lage eines [[Kartesisches Koordinatensystem|kartesischen Koordinatensystems]] in Bezug auf ein anderes kartesisches Koordinatensystem beschreiben und werden deshalb für [[Koordinatentransformation]]en verwendet. Oft ist das gedrehte Koordinatensystem an einen gedrehten Körper „angeheftet“. Man spricht dann vom ''körperfesten'' Koordinatensystem und nennt das ursprüngliche Koordinatensystem ''raumfest''. | ||
Die Drehlage wird erzeugt, indem der Körper aus seiner Ursprungslage heraus nacheinander um die drei Eulerwinkel um Koordinatenachsen [[Drehung|gedreht]] wird. Für die Wahl der Achsen gibt es verschiedene Konventionen: | |||
Die | |||
=== | * ''Eigentliche Eulerwinkel:'' Die erste und die dritte Drehung finden um die gleiche Koordinatenachse statt (z. B. Drehung um z-Achse, x-Achse, z-Achse). | ||
Die | * '''Kardanwinkel''' oder ''Tait-Bryan-Winkel'': Alle drei Drehungen werden um verschiedene Koordinatenachsen gedreht (z. B. in der Reihenfolge x-Achse, y-Achse, z-Achse). | ||
: < | Dabei wird entweder bei der zweiten und dritten Drehung um die zuvor gedrehten Koordinatenachsen gedreht (''intrinsische'' Drehungen) | ||
oder immer um die ursprünglichen Koordinatenachsen (''extrinsische'' Drehungen). | |||
Die aus den drei Einzeldrehungen zusammengesetzte Drehung kann durch eine [[Matrix (Mathematik)|Matrix]] beschrieben werden, die sich entsprechend als Produkt von drei elementaren [[Drehmatrix|Drehmatrizen]] darstellen lässt. Je nach Anwendungszweck betrachtet man verschiedene Matrizen: | |||
* [[Transformationsmatrix]] für die Koordinatentransformation vom gedrehten (körperfesten) ins ursprüngliche (raumfeste) Koordinatensystem, | |||
* Transformationsmatrix für die Koordinatentransformation vom raumfesten ins körperfeste Koordinatensystem, | |||
* [[Abbildungsmatrix]] der Drehung bezüglich des raumfesten Koordinatensystems. | |||
== Geschichte == | |||
[[Datei:Euler 1778.jpg|mini|Euler (1778)]] | |||
Drehungen wurden spätestens seit etwa 1600 durch drei Winkel beschrieben. So bestimmte [[Johannes Kepler]] in der ''[[Johannes Kepler#Astonomia nova|Astronomia nova]]'' die Orientierung der Marsbahn in Bezug auf die Ekliptik durch drei Winkel. Eine algebraische Beschreibung, mit der die Drehlage von beliebigen Punkten berechnet werden konnte, wurde aber erst ab 1775 von [[Leonhard Euler]] in zunehmender Tiefe formuliert.<ref name="ChengGupta89">{{Literatur |Autor=Hui Cheng, K. C. Gupta |Titel=A Historical Note on Final Rotations |Sammelwerk=Journal of Applied Mechanics |Band=56 |Nummer=1 |Datum=1989-03 |Seiten=139-145 |Online= [https://pdfs.semanticscholar.org/2d4f/d2652bb1a20cbe19229cea6acd43f6caee46.pdf Volltext] |Abruf=2018-12-13 |DOI=10.1115/1.3176034}}</ref> | |||
In der ersten Arbeit<ref name="E478">{{Literatur |Autor=L. Eulerus |Titel=Formulae generales pro translatione quacunque corporum rigidorum |Sammelwerk=Novi Commentarii academiae scientiarum Petropolitanae |Band=20 (1775) |Datum=1776 |Seiten=189-207 |Kommentar= ''translatio'' ist hier eine beliebige [[Bewegung (Mathematik)|Bewegung]] |Online= [http://www.17centurymaths.com/contents//euler/e478tr.pdf Online] mit englischer Übersetzung |Format=PDF |KBytes=188 |Abruf=2018-12-13}}</ref> | |||
zeigte er, dass die neun, den Elementen der Abbildungsmatrix entsprechenden, Koeffizienten wegen der [[Isometrie|Längentreue]] einer [[Bewegung (Mathematik)|Bewegung]] nicht unabhängig voneinander sind, sondern durch nur drei voneinander unabhängige Winkel festgelegt werden. Es handelt sich bei diesen aber nicht um die hier behandelten eulerschen Winkel, sondern um reine Rechengrößen ohne geometrische Bedeutung. Bekannt ist diese Arbeit heute besonders, weil er in einem Zusatz das heute nach ihm benannte [[Satz vom Fußball|Rotationstheorem]] bewies, nach dem jede [[Bewegung (Mathematik)|eigentliche Bewegung]] mit einem Fixpunkt eine Drehung um eine Achse ist. Die aus diesem Ergebnis resultierenden Abbildungsgleichungen, in denen eine Drehung durch die [[Richtungskosinus]] der Drehachse und den Drehwinkel parametrisiert wird, fand er in einer kurz darauf folgenden zweiten Arbeit.<ref name="E479">{{Literatur |Autor=L. Eulerus |Titel=Nova methodus motum corporum rigidorum determinandi |Sammelwerk=Novi Commentarii academiae scientiarum Petropolitanae |Band=20 (1775) |Datum=1776 |Seiten=208-238 |Kommentar=die Abbildungsgleichungen stehen in §13 |Online= [http://math.dartmouth.edu/~euler/docs/originals/E479.pdf Online] |Format=PDF |KBytes=1600 |Abruf=2018-12-13}}</ref> | |||
\ | [[Datei:Euler angles (Euler's paper E825).png|mini|Winkel <math>p</math>, <math>q</math>, <math>r</math> aus der Arbeit<ref name="E825" /> von Euler]] | ||
</math> | In einer dritten, erst [[postum]] erschienenen Arbeit<ref name="E825">{{Literatur |Autor=Leonardus Eulerus |Titel=De motu corporum circa punctum fixum mobilium |Sammelwerk=Leonardi Euleri opera postuma mathematica et physica : anno MDCCCXLIV detecta |Band=2 |Datum=1862 |Seiten=43-62 |Online= [http://math.dartmouth.edu/~euler/docs/originals/E825.pdf Online] |Format=PDF |KBytes=1400 |Abruf=2018-12-13}} – [http://math.dartmouth.edu/~euler/docs/originals/E825.figure.pdf zugehörige Abbildungen]</ref> | ||
führte er schließlich drei Winkel <math>p</math>, <math>q</math> und <math>r</math> ein, mit denen er die Transformation von körperfesten in raumfeste Koordinaten beschrieb und die bis auf Vorzeichen und additive Konstanten mit den heute nach ihm benannten Winkeln übereinstimmen. Sein Vorgehen unterschied sich dabei deutlich vom heute gängigen Verfahren, bei dem das eine Koordinatensystem durch drei aufeinanderfolgende Drehungen um die Koordinatenachsen in das andere Koordinatensystem überführt wird. | |||
Euler argumentiere ähnlich wie bei der ersten Arbeit, kommt aber zu einem günstigeren Ansatz<ref name="E825" />{{rp|S. 50}} mit den drei Winkeln <math>p</math>, <math>q</math> und <math>r</math>, weil er hier – in moderner Sprechweise – nicht nur die Orthonormalität der Zeilen, sondern auch die der Spalten der Transformationsmatrix verwendete. Zur Klärung ihrer geometrischen Bedeutung betrachtete er die Schnittpunkte <math>a</math>, <math>b</math>, <math>c</math> des raumfesten Koordinatensystems mit der Einheitskugel und die entsprechenden Schnittpunkte <math>A</math>, <math>B</math>, <math>C</math> des körperfesten Systems und zeigte, dass die Kosinusse der Bögen <math>aA</math>, <math>aB</math>, …, <math>cC</math> gerade die Koeffizienten der Transformationsgleichungen sind. Es ist also <math>p=aA</math> der Winkel zwischen der <math>x</math>- und der <math>X</math>-Achse. Außerdem zeigt sich mittels [[Sphärische Trigonometrie|sphärischer Trigonometrie]], dass <math>q</math> der Winkel bei <math>A</math> im Kugeldreieck <math>ABa</math> und <math>r</math> der Winkel bei <math>a</math> im Kugeldreieck <math>abA</math> ist. Heute werden die entsprechenden Winkel nicht von der <math>xX</math>-Ebene, sondern von der zu ihr senkrechten Knotenlinie <math>N</math> aus gemessen; der Zusammenhang mit den heute meist verwendeten Eulerwinkeln für die Drehfolge x-y-x ist gegeben durch <math>\alpha= r+90^{\circ}</math>, <math>\beta=p</math> und <math>\gamma=-q+90^{\circ}</math>. | |||
[[Joseph-Louis Lagrange|Lagrange]] brachte in der 1788 erschienenen ''Mécanique Analytique''<ref name="Lagrange">{{Literatur |Autor=La Grange |Titel=Analytische Mechanik |Ort=Göttingen |Datum=1797 |Originaltitel=Mécanique Analytique |Originaljahr=1788 |Übersetzer=Friedrich Wilhelm August Murhard |Online= [https://archive.org/download/analytischemech00murhgoog/analytischemech00murhgoog.pdf Scan] |Format=PDF |KBytes= |Abruf=2018-12-13}}</ref> | |||
zwei Ableitungen der Transformationsgleichungen. Die erste<ref name="Lagrange" />{{rp|S. 381–388}} stimmt bis auf die Namen der Winkel (bei ihm heißen sie <math>\lambda=p</math>, <math>\mu=r</math> und <math>\nu=q</math>) im Wesentlichen mit der von Euler überein. Die zweite<ref name="Lagrange" />{{rp|S. 398–401}} deckt sich mit der modernen, unten ausführlich behandelten Darstellung für die z-x-z-Drehfolge – wiederum mit anderen Winkelnamen (<math>\varphi=\gamma</math>, <math>\psi=\alpha</math>, <math>\omega=\beta</math>). <!-- Bei Lagrange Vorzeichenfehler auf S. 400: Koeffizient vor b in Gleichung für b''' --> | |||
== Eigentliche Eulerwinkel == | |||
[[Datei:Eulerangles.svg|mini|hochkant=1|Koordinatentransformation, Drehfolge in Standard-x-Konvention<br /> | |||
<span style="color:#00BFF0">blau</span>: Koordinatensystem in Ausgangslage<br /> | |||
<span style="color:green">grün</span>: Schnittgerade der xy-Ebenen, Zwischenlage der x-Achse<br /> | |||
<span style="color:red">rot</span>: Koordinatensystem in Ziellage]] | |||
Im Folgenden werden wie in der nebenstehenden Grafik die Achsen des Koordinatensystems in Ausgangslage (in der Grafik blau) mit den Kleinbuchstaben <math>x</math>, <math>y</math> und <math>z</math>, die Achsen in Ziellage (in der Grafik rot) mit den entsprechenden Großbuchstaben <math>X</math>, <math>Y</math> und <math>Z</math> bezeichnet. | |||
=== Geometrische Beschreibung === | |||
Die <math>x</math>-<math>y</math>-Ebene und die <math>X</math>-<math>Y</math>-Ebene schneiden sich in einer Geraden <math>N</math> (Knotenlinie). Diese steht senkrecht auf der <math>z</math>-Achse und auf der <math>Z</math>-Achse. | |||
*Der erste Euler-Winkel <math>\alpha</math> (auch <math>\varphi</math>) ist der Winkel zwischen der <math>x</math>-Achse und der Geraden <math>N</math> (gemessen in Richtung der y-Achse). | |||
*Der zweite Euler-Winkel <math>\beta</math> (auch <math>\theta</math>) ist der Winkel zwischen der <math>z</math>-Achse und der <math>Z</math>-Achse. | |||
*Der dritte Euler-Winkel <math>\gamma</math> (auch <math>\psi</math>) ist der Winkel zwischen <math>N</math> und der <math>X</math>-Achse. | |||
Die hier beschriebene Version der eulerschen Winkel, bei der der Winkel <math>\alpha</math> von der <math>x</math>-Achse aus zur Knotenlinie und der Winkel <math>\gamma</math> von der Knotenlinie zur <math>X</math>-Achse gemessen wird, nennt man die ''Standard-x-Konvention''. Entsprechend werden bei der ''Standard-y-Konvention'' die Winkel von der <math>y</math>-Achse zur Knotenlinie und von der Knotenlinie zur <math>Y</math>-Achse gemessen. | |||
In der Physik wird meist die Standard-x-Konvention verwendet. Statt wie hier mit <math>\alpha</math>, <math>\beta</math> und <math>\gamma</math> werden die Winkel meist mit <math>\varphi</math>, <math>\theta</math> und <math>\psi</math> bezeichnet. | |||
=== Beschreibung durch intrinsische Drehungen === | |||
Die Drehung <math>r</math>, welche das <math>xyz</math>-System in das <math>XYZ</math>-System dreht, kann in drei Drehungen aufgeteilt werden. Bei der Standard-x-Konvention sind das: | |||
* Zunächst die Drehung <math>r_z(\alpha)</math> um den Winkel <math>\alpha</math> um die <math>z</math>-Achse, | |||
* dann die Drehung <math>r_{N}(\beta)</math> um den Winkel <math>\beta</math> um die Knotenlinie <math>N</math>, | |||
* zuletzt die Drehung <math>r_{Z}(\gamma)</math> um den Winkel <math>\gamma</math> um die <math>Z</math>-Achse. | |||
Bei diesen Drehungen entstehen nacheinander neue Koordinatensysteme: | |||
*ursprüngliches Koordinatensystem: <math>x</math>-, <math>y</math>- und <math>z</math>-Achse | |||
*nach der ersten Drehung: <math>x'</math>-, <math>y'</math>- und <math>z'</math>-Achse | |||
*nach der zweiten Drehung: <math>x''</math>-, <math>y''</math>- und <math>z''</math>-Achse | |||
*nach der dritten Drehung: <math>x'''</math>-, <math>y'''</math>- und <math>z'''</math>-Achse (bzw. <math>X</math>-, <math>Y</math>- und <math>Z</math>-Achse) | |||
Die Drehung um <math>N</math> ist also eine Drehung um die <math>x'</math>-Achse, die Drehung um die <math>Z</math>-Achse eine Drehung um die <math>z''</math>-Achse. Die Gesamtdrehung <math>r</math> setzt sich also aus den Drehungen <math>r_z(\alpha)</math>, <math>r_{x'}(\beta)</math> und <math>r_{z''}(\gamma)</math> zusammen: | |||
:<math>r = r_{z''}(\gamma) \circ r_{x'}(\beta) \circ r_z(\alpha)</math> | |||
<!-- | |||
Bei der oben beschriebenen Standard-x-Konvention wird zunächst um die <math>z</math>-Achse um den Winkel <math>\alpha</math> gedreht. Die <math>x</math>-Achse wird dabei auf die Knotenlinie <math>N</math> abgebildet, die neue <math>x'</math>-Achse. Die <math>z</math>-Achse bleibt fest (<math>z'</math>-Achse = <math>z</math>-Achse). Es folgt eine Drehung um den Winkel <math>\beta</math> um die <math>x'</math>-Achse. Die <math>z'</math>-Achse wird dabei auf die <math>z''</math>-Achse abgebildet. Zuletzt wird um den Winkel <math>\gamma</math> um diese neue <math>z''</math>-Achse gedreht. Die <math>x'</math>-Achse (= <math>x''</math>-Achse) wird dabei auf die <math>X</math>-Achse abgebildet. Die <math>z''</math>-Achse bleibt fest und ist die neue <math>Z</math>-Achse. | |||
--> | |||
Die Reihenfolge der Drehachsen ist also: <math>z</math>-Achse → <math>x'</math>-Achse → <math>z''</math>-Achse oder kurz <math>z</math>-<math>x'</math>-<math>z''</math>. | |||
Eine solche Zerlegung in Drehungen, bei denen jeweils um die mitgedrehten Koordinatenachsen gedreht wird, nennt man ''intrinsische'' Drehfolge. | |||
=== Beschreibung durch extrinsische Drehungen === | |||
=== | [[Datei:Euler angles zxz ext+axes.png|mini|Eulerwinkel bei extrinsischen Einzeldrehungen in der Reihenfolge <math>z</math>-<math>x</math>-<math>z</math> mit den Winkeln <math>\gamma</math>, <math>\beta</math>, <math>\alpha</math>. | ||
<span style="color:#0033CC">blau</span>: Ausgangslage des Koordinatensystems, | |||
<span style="color:#FF0000">rot</span>: Ziellage, | |||
<span style="color:#339900">grün</span>: Schnittgerade der beiden xy-Ebenen.]] | |||
Dieselbe Drehung <math>r</math> kann auch durch drei Einzeldrehungen um die ursprünglichen Koordinatenachsen beschrieben werden. Dabei bleiben die Winkel gleich, aber die Reihenfolge der Drehungen kehrt sich um, und die Zwischenlagen <math>x'y'z'</math> und <math>x''y''z''</math> sind andere als bei der intrinsischen Drehung: | |||
Zuerst wird der Körper um den Winkel <math>\gamma</math> um die <math>z</math>-Achse gedreht, dann um <math>\beta</math> um die <math>x</math>-Achse (der Winkel zwischen der <math>x</math>- und <math>x''</math>-Achse ist derselbe wie der zwischen der <math>x</math>- und der <math>x'</math>-Achse, nämlich <math>\gamma</math>) und zuletzt um den Winkel <math>\alpha</math> um die <math>z</math>-Achse (dabei wird die <math>x</math>-Achse in die Knotenlinie <math>N</math> gedreht und der Winkel zwischen <math>N</math> und der <math>X</math>-Achse ist <math>\gamma</math>). | |||
Eine algebraische Begründung findet sich weiter unten im Abschnitt [[#Matrix-Herleitung im allgemeinen Fall|Matrix-Herleitung im allgemeinen Fall]]. Es ist also | |||
:<math>r=r_z(\alpha) \circ r_x(\beta) \circ r_z(\gamma)</math>. | |||
Eine solche Drehfolge, bei der immer um die ursprünglichen Koordinatenachsen gedreht wird, heißt ''extrinsische'' Drehfolge. | |||
Die Beschreibungen durch intrinsische und durch extrinsische Drehungen sind also äquivalent. Die Beschreibung durch intrinsische Drehungen ist jedoch anschaulicher, während die Beschreibung durch extrinsische Drehungen mathematisch leichter zugänglich ist. | |||
=== Beschreibung durch Matrizen === | |||
Die Drehungen um die Eulerschen Winkel können mit Hilfe von [[Drehmatrix|Drehmatrizen]], deren Einträge [[Sinus und Kosinus|Sinus- und Kosinus]]-Werte der Euler-Winkel sind, beschrieben werden. Dabei unterscheidet man zwischen [[Abbildungsmatrix|Abbildungsmatrizen]] und [[Transformationsmatrix|Koordinatentransformationsmatrizen]]. Im Folgenden werden diese Matrizen für die Standard-x-Konvention angegeben. | |||
Die Matrizen für die Standard-y-Konvention erhält man analog, indem man statt der elementaren Drehmatrix für die Drehung um die x-Achse die Drehmatrix für die Drehung um die y-Achse verwendet. | |||
==== Abbildungsmatrix (aktive Drehung) ==== | |||
Bei einer ''aktiven Drehung'' (''Alibi-Drehung'') werden die Punkte und [[Vektor]]en des Raums gedreht. Das Koordinatensystem wird festgehalten. Die Drehmatrix <math>R</math> ist die [[Abbildungsmatrix]] dieser [[Lineare Abbildung|Abbildung]]. Die Koordinaten des gedrehten Vektors <math>\vec w=r(\vec v)</math> ergeben sich aus den Koordinaten des ursprünglichen Punkts <math>\vec v</math> durch [[Matrix-Vektor-Produkt|Multiplikation]] mit der Drehmatrix: | |||
: <math> | |||
\begin{pmatrix} w_x \\ w_y \\ w_z \\ \end{pmatrix} = R \begin{pmatrix} v_x \\ v_y \\ v_z \\ \end{pmatrix} \,. | |||
</math> | |||
[[ | Die [[Abbildungsmatrix|Abbildungsmatrizen]] für Drehungen um die Koordinatenachsen (elementare Drehmatrizen) lauten: | ||
< | :<math> | ||
< | R_x(\alpha) = \begin{pmatrix} | ||
1 & 0 & 0 \\ | |||
0 & \cos \alpha & -\sin \alpha \\ | |||
0 & \sin \alpha & \cos \alpha | |||
\end{pmatrix}, \quad | |||
R_y(\alpha) = \begin{pmatrix} | |||
\cos \alpha & 0 & \sin \alpha \\ | |||
0 & 1 & 0 \\ | |||
-\sin \alpha & 0 & \cos \alpha | |||
\end{pmatrix}, \quad | |||
R_z(\alpha) = \begin{pmatrix} | |||
\cos \alpha & -\sin \alpha & 0 \\ | |||
\sin \alpha & \cos \alpha & 0 \\ | |||
0 & 0 & 1 | |||
\end{pmatrix} | |||
</math> | |||
für die Drehung um den Winkel <math>\alpha</math> um die <math>x</math>-Achse, die <math>y</math>-Achse und die <math>z</math>-Achse. | |||
Die Drehmatrix der zusammengesetzten Drehung erhält man durch [[Matrizenmultiplikation|Matrixmultiplikation]] aus den Matrizen der einzelnen Drehungen. Da die elementaren Drehmatrizen die Drehungen um die ursprünglichen Koordinatenachsen beschreiben, verwendet man die extrinsische Drehfolge | |||
:<math>r=r_z(\alpha) \circ r_x(\beta) \circ r_z(\gamma)</math> | |||
und erhält die Abbildungsmatrix | |||
: <math> | : <math> | ||
\begin{align} | \begin{align} | ||
R_{zxz} & = R_z(\alpha)\, R_x(\beta)\, R_z(\gamma) \\ | |||
& = \begin{pmatrix} | |||
\cos \ | \cos \alpha & -\sin \alpha & 0 \\ | ||
\sin \alpha & \cos \alpha & 0 \\ | |||
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{pmatrix} | \end{pmatrix} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
1 & 0 & 0 \\ | 1 & 0 & 0 \\ | ||
0 & \cos \beta & \sin \beta \\ | 0 & \cos \beta & -\sin \beta \\ | ||
0 & | 0 & \sin \beta & \cos \beta | ||
\end{pmatrix} | \end{pmatrix} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
\cos \ | \cos \gamma & -\sin \gamma & 0 \\ | ||
\sin \gamma & \cos \gamma & 0 \\ | |||
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{pmatrix}\\ | \end{pmatrix}\\ | ||
&= \begin{pmatrix} | |||
\begin{pmatrix} | |||
\cos \alpha \cos \gamma - \sin \alpha \cos \beta \sin \gamma | \cos \alpha \cos \gamma - \sin \alpha \cos \beta \sin \gamma | ||
& | & - \cos \alpha \sin \gamma - \sin \alpha \cos \beta \cos \gamma | ||
& \sin \ | & \sin \alpha \sin \beta \\ | ||
\sin \alpha \cos \gamma + \cos \alpha \cos \beta \sin \gamma | |||
& - \sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma | & - \sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma | ||
& | & - \cos \alpha \sin \beta \\ | ||
\sin \ | \sin \beta \sin \gamma | ||
& | & \sin \beta \cos \gamma | ||
& \cos \beta | & \cos \beta | ||
\end{pmatrix} | \end{pmatrix} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
==== Transformationsmatrix ==== | |||
Die | Transformationsmatrizen beschreiben Koordinatentransformationen vom ursprünglichen (raumfesten) Koordinatensystem ins gedrehte (körperfeste) oder umgekehrt. Die Transformationsmatrix für die Koordinatentransformation vom körperfesten Koordinatensystem ins raumfeste stimmt mit der oben beschriebenen Abbildungsmatrix überein, die Matrix für die umgekehrte Transformation ist die Transponierte dieser Matrix. Hat der Vektor <math>\vec v</math> im raumfesten Koordinatensystem die Koordinaten <math>v_x, v_y, v_z</math> und im körperfesten die Koordinaten <math>v_X, v_Y, v_Z</math>, so gilt | ||
: <math> | :<math> | ||
\begin{align} | \begin{align} | ||
\begin{pmatrix}v_x \\ v_y \\ v_z \end{pmatrix} | |||
\begin{pmatrix} | &= R_{zxz} \begin{pmatrix}v_X \\ v_Y \\ v_Z \end{pmatrix} \\ | ||
\cos \alpha \cos \gamma - \sin \alpha \cos \beta \sin \gamma | &= R_z(\alpha)\, R_x(\beta)\, R_z(\gamma) \begin{pmatrix}v_X \\ v_Y \\ v_Z \end{pmatrix}\\ | ||
& = \begin{pmatrix} | |||
\cos \alpha & -\sin \alpha & 0 \\ | |||
\sin \alpha & \cos \alpha & 0 \\ | |||
\sin \alpha \cos \gamma + \cos \alpha \cos \beta \sin \gamma | 0 & 0 & 1 | ||
\end{pmatrix} | |||
\begin{pmatrix} | |||
1 & 0 & 0 \\ | |||
\sin \beta \sin \gamma | 0 & \cos \beta & -\sin \beta \\ | ||
0 & \sin \beta & \cos \beta | |||
\end{pmatrix} | |||
\end{pmatrix} | \begin{pmatrix} | ||
\cos \gamma & -\sin \gamma & 0 \\ | |||
\sin \gamma & \cos \gamma & 0 \\ | |||
0 & 0 & 1 | |||
\end{pmatrix} | |||
\begin{pmatrix}v_X \\ v_Y \\ v_Z \end{pmatrix}\\ | |||
&= \begin{pmatrix} | |||
\cos \alpha \cos \gamma - \sin \alpha \cos \beta \sin \gamma & | |||
- \cos \alpha \sin \gamma - \sin \alpha \cos \beta \cos \gamma & | |||
\sin \alpha \sin \beta \\ | |||
\sin \alpha \cos \gamma + \cos \alpha \cos \beta \sin \gamma & | |||
- \sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma & | |||
- \cos \alpha \sin \beta \\ | |||
\sin \beta \sin \gamma & | |||
\sin \beta \cos \gamma & | |||
\cos \beta | |||
\end{pmatrix} | |||
\begin{pmatrix}v_X \\ v_Y \\ v_Z \end{pmatrix} | |||
\end{align} | \end{align} | ||
</math> | </math> | ||
und | |||
: <math> | : <math> | ||
\begin{align} | \begin{align} | ||
\begin{pmatrix}v_X \\ v_Y \\ v_Z \end{pmatrix} | |||
& = R_{zxz}^T \begin{pmatrix}v_x \\ v_y \\ v_z \end{pmatrix} \\ | |||
& = R_z(\gamma)^T\, R_x(\beta)^T\, R_z(\alpha)^T \begin{pmatrix}v_x \\ v_y \\ v_z \end{pmatrix} \\ | |||
-\sin \gamma & \cos \gamma & 0 \\ | & = \begin{pmatrix} | ||
\cos \gamma & \sin \gamma & 0 \\ | |||
-\sin \gamma & \cos \gamma & 0 \\ | |||
0 & 0 & 1 | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
1 & 0 & 0 \\ | |||
0 & \cos \beta & \sin \beta \\ | |||
0 & -\sin \beta & \cos \beta | |||
\end{pmatrix} | \end{pmatrix} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
\cos \alpha & \sin \alpha & 0 \\ | |||
-\sin \alpha & \cos \alpha & 0 \\ | |||
0 & 0 & 1 | |||
\end{pmatrix} | \end{pmatrix} | ||
\begin{pmatrix}v_x \\ v_y \\ v_z \end{pmatrix} \\ | |||
& = | |||
\begin{pmatrix} | \begin{pmatrix} | ||
\cos \alpha \cos \gamma - \sin \alpha \cos \beta \sin \gamma & | |||
\sin \alpha \cos \gamma + \cos \alpha \cos \beta \sin \gamma & | |||
\sin \beta \sin \gamma \\ | |||
\end{pmatrix} \\ | - \cos \alpha \sin \gamma - \sin \alpha \cos \beta \cos \gamma & | ||
- \sin \alpha \sin \gamma + \cos \alpha \cos \beta \cos \gamma & | |||
\sin \beta \cos \gamma \\ | |||
\sin \alpha \sin \beta & | |||
-\cos \alpha \sin \beta & | |||
\cos \beta | |||
\end{pmatrix} | |||
\begin{pmatrix}v_x \\ v_y \\ v_z \end{pmatrix} . | |||
\end{align} | \end{align} | ||
</math> | </math> | ||
=== Konventionen === | |||
Es gibt sechs verschiedene Möglichkeiten, die Achsen für eigentliche Eulerwinkel zu wählen. Bei allen ist die erste und die dritte Achse die gleiche. Die sechs Möglichkeiten sind: | |||
*<math>z</math>-<math>x'</math>-<math>z''</math> (intrinsisch) bzw. <math>z</math>-<math>x</math>-<math>z</math> (extrinsisch): Standard-x-Konvention | |||
*<math>z</math>-<math>y'</math>-<math>z''</math> (intrinsisch) bzw. <math>z</math>-<math>y</math>-<math>z</math> (extrinsisch): Standard-y-Konvention | |||
*<math>y</math>-<math>z'</math>-<math>y''</math> (intrinsisch) bzw. <math>y</math>-<math>z</math>-<math>y</math> (extrinsisch) | |||
*<math>y</math>-<math>x'</math>-<math>y''</math> (intrinsisch) bzw. <math>y</math>-<math>x</math>-<math>y</math> (extrinsisch) | |||
*<math>x</math>-<math>y'</math>-<math>x''</math> (intrinsisch) bzw. <math>x</math>-<math>y</math>-<math>x</math> (extrinsisch) | |||
*<math>x</math>-<math>z'</math>-<math>x''</math> (intrinsisch) bzw. <math>x</math>-<math>z</math>-<math>x</math> (extrinsisch) | |||
== Kardan-Winkel == | |||
Bei den ''Kardan-Winkeln'' (nach [[Gerolamo Cardano]]) oder auch ''Tait-Bryan-Winkeln'' (benannt nach [[Peter Guthrie Tait]] und [[George Hartley Bryan]]) erfolgen die drei Drehungen um drei verschiedene Achsen. Wie bei den eigentlichen Eulerwinkeln gibt es sechs mögliche Drehfolgen: | |||
*<math>z</math>-<math>y'</math>-<math>x''</math> (intrinsisch) bzw. <math>x</math>-<math>y</math>-<math>z</math> (extrinsisch) | |||
*<math>z</math>-<math>x'</math>-<math>y''</math> (intrinsisch) bzw. <math>y</math>-<math>x</math>-<math>z</math> (extrinsisch) | |||
*<math>y</math>-<math>z'</math>-<math>x''</math> (intrinsisch) bzw. <math>x</math>-<math>z</math>-<math>y</math> (extrinsisch) | |||
*<math>y</math>-<math>x'</math>-<math>z''</math> (intrinsisch) bzw. <math>z</math>-<math>x</math>-<math>y</math> (extrinsisch) | |||
*<math>x</math>-<math>y'</math>-<math>z''</math> (intrinsisch) bzw. <math>z</math>-<math>y</math>-<math>x</math> (extrinsisch) | |||
*<math>x</math>-<math>z'</math>-<math>y''</math> (intrinsisch) bzw. <math>y</math>-<math>z</math>-<math>x</math> (extrinsisch) | |||
=== Roll-, Nick- und Gierwinkel: z-y′-x″-Konvention === | |||
==== Beschreibung ==== | |||
[[Datei:Taitbrianzyx.svg|mini|Drehfolge z, y′, x″ (Gier-Nick-Roll)<br /> | |||
<span style="color:#00BFF0">blau</span>: raumfestes Koordinatensystem<br /> | |||
<span style="color:green">grün</span>: y'-Achse = Knotenlinie N(y′)<br /> | |||
<span style="color:red">rot</span>: körperfestes Koordinatensystem<br /> | |||
Anmerkung: <math>\theta</math> ist hier negativ.]] | |||
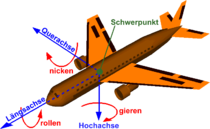
[[Datei:Plane.svg|mini|Gier-, Nick- und Rollwinkel<math>(\psi, \theta, \varphi)</math> als Lagewinkel eines Flugzeugs]] | |||
{{Siehe auch|Roll-Nick-Gier-Winkel}} | |||
Die in der Luftfahrt, Schifffahrt und dem Automobilbau angewendeten und genormten (Luftfahrt: [[DIN-Norm|DIN]] 9300; Automobilbau: [[DIN-Norm|DIN ISO]] 8855) Drehfolgen gehören in die Gruppe der Tait-Bryan-Drehungen. In den Normen sind die Namen [[Roll-Nick-Gier-Winkel|Gier-, Nick- und Roll-Winkel]] (engl. ''yaw'', ''pitch'' and ''roll angle'') für die drei Euler-Winkel vorgeschrieben. Durch die drei Drehungen wird das erdfeste <math>xyz</math>-System (engl. ''world frame'') in das körperfeste <math>XYZ</math>-Koordinatensystem (engl. ''body frame'') gedreht. | |||
< | |||
< | |||
</ | |||
Intrinsische Reihenfolge <math>z</math>-<math>y'</math>-<math>x''</math> (Gier-Nick-Roll-Winkel): | |||
* Mit dem im erdfesten System gemessenen [[Gierwinkel]] '''<math>\psi</math>''' (auch Steuerkurs oder Azimut genannt) wird um die <math>z</math>-Achse gedreht. Die <math>y</math>-Achse wird zur Knotenachse <math>N(y')</math>.<br />Hauptwertebereich: <math>- \pi < \psi \le \pi</math>. Die Drehrichtung ist mathematisch positiv (gegen den Uhrzeigersinn) | |||
< | * Mit dem gegen die Erdoberfläche (<math>x</math>-<math>y</math>-Ebene) gemessenen [[Nickwinkel]] '''<math>\theta</math>''' wird um die Knotenachse <math>N(y')</math> gedreht. Es entsteht die fahrzeugfeste <math>X</math>-Achse.<br />Hauptwertebereich: <math>- \frac{\pi}{2} \le \theta \le \frac{\pi}{2}</math>. Die Drehrichtung ist mathematisch positiv. | ||
< | |||
< | |||
* Der [[Rollwinkel]] '''<math>\varphi</math>''' (auch Wankwinkel genannt) beschreibt die Drehung um die fahrzeugfeste <math>X</math>-Achse. Es entstehen die fahrzeugfesten Achsen <math>Y</math> und <math>Z</math>.<br />Hauptwertebereich: <math>- \pi < \varphi \le \pi</math>. Die Drehrichtung ist mathematisch positiv. | |||
Extrinsisch entspricht dies der Reihenfolge <math>x</math>-<math>y</math>-<math>z</math> (Roll-Nick-Gier-Winkel). | |||
Statt der Kleinbuchstaben <math>\psi</math>, <math>\theta</math> und <math>\varphi</math> werden auch die entsprechenden Großbuchstaben <math>\Psi</math>, <math>\Theta</math> und <math>\Phi</math> verwendet. | |||
<math> | ==== Transformationsmatrizen ==== | ||
Die Koordinatentransformation vom körperfesten ins raumfeste Koordinatensystem wird durch die Matrix | |||
:<math> | |||
\begin{align} | \begin{align} | ||
R_{GNR} & = R_z(\psi) \, R_y(\theta) \, R_x(\varphi)\\ | |||
\begin{pmatrix} | &= | ||
\begin{pmatrix} | |||
\cos \psi & - \sin \psi & 0 \\ | |||
\sin \psi & \cos \psi & 0 \\ | |||
0 & 0 & 1 | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
\cos \theta & 0 & \sin \theta \\ | |||
0 & 1 & 0 \\ | |||
- \sin \theta & 0 & \cos \theta | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
1 & 0 & 0 \\ | |||
0 & \cos \varphi & -\sin \varphi \\ | |||
0 & \sin \varphi & \cos \varphi | |||
\end{pmatrix}\\ | |||
&= | |||
\begin{pmatrix} | |||
\cos \theta \cos \psi & | |||
\sin \varphi \sin \theta \cos \psi - \cos \varphi \sin \psi & | |||
\cos \varphi \sin \theta \cos \psi + \sin \varphi \sin \psi \\ | |||
\cos \theta \sin \psi & | |||
\sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi & | |||
\cos \varphi \sin \theta \sin \psi - \sin \varphi \cos \psi \\ | |||
-\sin \theta & | |||
\sin \varphi \cos \theta & | |||
\cos \varphi \cos \theta | |||
\end{pmatrix} | |||
\end{align} | |||
</math> | |||
beschrieben. Die umgekehrte Transformation vom raumfesten ins körperfeste Koordinatensystem wird durch die Transponierte dieser Matrix beschrieben. (Eigentlich die Inverse, aber bei Drehmatrizen stimmt die inverse mit der transponierten Matrix überein.) | |||
:<math> | |||
\begin{align} | |||
R_{GNR}^T & = R_x(\varphi)^T \, R_y(\theta)^T \, R_z(\psi)^T\\ | |||
&= | |||
\begin{pmatrix} | |||
1 & 0 & 0 \\ | 1 & 0 & 0 \\ | ||
0 & \cos \ | 0 & \cos \varphi & \sin \varphi \\ | ||
0 & - \sin \ | 0 & - \sin \varphi & \cos \varphi | ||
\end{pmatrix} | \end{pmatrix} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
\cos \ | \cos \theta & 0 & - \sin \theta \\ | ||
0 & 1 & 0 \\ | 0 & 1 & 0 \\ | ||
\sin \ | \sin \theta & 0 & \cos \theta | ||
\end{pmatrix} | \end{pmatrix} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
\cos \ | \cos \psi & \sin \psi & 0 \\ | ||
- \sin \ | - \sin \psi & \cos \psi & 0 \\ | ||
0 & 0 & 1 | 0 & 0 & 1 | ||
\end{pmatrix}\\ | |||
& = | |||
\begin{pmatrix} | |||
\cos \theta \cos \psi & | |||
\cos \theta \sin \psi & | |||
-\sin \theta \\ | |||
\sin \varphi \sin \theta \cos \psi - \cos \varphi \sin \psi & | |||
\sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi & | |||
\sin \varphi \cos \theta \\ | |||
\cos \varphi \sin \theta \cos \psi + \sin \varphi \sin \psi & | |||
\cos \varphi \sin \theta \sin \psi - \sin \varphi \cos \psi & | |||
\cos \varphi \cos \theta | |||
\end{pmatrix} | \end{pmatrix} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
<math> | Das bedeutet: Hat der Vektor <math>\vec v</math> im raumfesten System die Koordinaten <math>v_x</math>, <math>v_y</math>, <math>v_z</math> und im körperfesten System die Koordinaten <math>v_X</math>, <math>v_Y</math>, <math>v_Z</math>, so gilt | ||
:<math> | |||
\begin{align} | \begin{align} | ||
\begin{pmatrix} v_x \\v_y \\ v_z \end{pmatrix} &= | |||
\begin{pmatrix} | |||
\cos \psi & - \sin \psi & 0 \\ | |||
\sin \psi & \cos \psi & 0 \\ | |||
0 & 0 & 1 | |||
\end{pmatrix} | |||
\begin{pmatrix} | \begin{pmatrix} | ||
\cos \theta & 0 & \sin \theta \\ | |||
0 & 1 & 0 \\ | |||
- \sin \theta & 0 & \cos \theta | |||
\end{pmatrix} | \end{pmatrix} | ||
\begin{pmatrix} | |||
1 & 0 & 0 \\ | |||
0 & \cos \varphi & -\sin \varphi \\ | |||
0 & \sin \varphi & \cos \varphi | |||
\end{pmatrix} | |||
\begin{pmatrix} v_X \\v_Y \\ v_Z \end{pmatrix}\\ | |||
&= | |||
\begin{pmatrix} | |||
\cos \theta \cos \psi & | |||
\sin \varphi \sin \theta \cos \psi - \cos \varphi \sin \psi & | |||
\cos \varphi \sin \theta \cos \psi + \sin \varphi \sin \psi \\ | |||
\cos \theta \sin \psi & | |||
\sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi & | |||
\cos \varphi \sin \theta \sin \psi - \sin \varphi \cos \psi \\ | |||
-\sin \theta & | |||
\sin \varphi \cos \theta & | |||
\cos \varphi \cos \theta | |||
\end{pmatrix} | |||
\begin{pmatrix} v_X \\v_Y \\ v_Z \end{pmatrix} | |||
\end{align} | |||
</math> | |||
und | |||
:<math> | |||
\begin{align} | |||
\begin{pmatrix} v_X \\v_Y \\ v_Z \end{pmatrix} &= | |||
\begin{pmatrix} | |||
1 & 0 & 0 \\ | |||
0 & \cos \varphi & \sin \varphi \\ | |||
0 & - \sin \varphi & \cos \varphi | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
\cos \theta & 0 & - \sin \theta \\ | |||
0 & 1 & 0 \\ | |||
\sin \theta & 0 & \cos \theta | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
\cos \psi & \sin \psi & 0 \\ | |||
- \sin \psi & \cos \psi & 0 \\ | |||
0 & 0 & 1 | |||
\end{pmatrix} | |||
\begin{pmatrix} v_x \\v_y \\ v_z \end{pmatrix}\\ | |||
&= | |||
\begin{pmatrix} | |||
\cos \theta \cos \psi & | |||
\cos \theta \sin \psi & | |||
-\sin \theta \\ | |||
\sin \varphi \sin \theta \cos \psi - \cos \varphi \sin \psi & | |||
\sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi & | |||
\sin \varphi \cos \theta \\ | |||
\cos \varphi \sin \theta \cos \psi + \sin \varphi \sin \psi & | |||
\cos \varphi \sin \theta \sin \psi - \sin \varphi \cos \psi & | |||
\cos \varphi \cos \theta | |||
\end{pmatrix} | |||
\begin{pmatrix} v_x \\v_y \\ v_z \end{pmatrix} | |||
\end{align} | \end{align} | ||
</math | </math> | ||
=====Anwendungsbeispiel===== | ===== Anwendungsbeispiel ===== | ||
Der Gewichtsvektor | Der Gewichtsvektor <math>\vec G</math> hat im erdfesten <math>xyz</math>-Koordinatensystem nur eine <math>z</math>-Komponente (in Richtung Erdmittelpunkt): | ||
: <math> | : <math> | ||
G_E = | \vec G_E = \begin{pmatrix} 0 \\ 0 \\ mg \end{pmatrix} | ||
</math> | </math> | ||
Die Transformation ins flugzeugfeste Koordinatensystem geschieht dann durch | Die Transformation ins flugzeugfeste Koordinatensystem geschieht dann durch Multiplikation des erdfesten Gewichtsvektors <math>\vec G_E</math> mit der Transformationsmatrix <math>R_{GNR}^T</math>: | ||
: <math> | : <math> | ||
\begin{align} | \begin{align} | ||
G_F &= | \vec G_F &= R_{GNR}^T \, \vec G_E \\ | ||
& = | & = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
\cos \ | \cos \theta \cos \psi & | ||
\cos \ | \cos \theta \sin \psi & | ||
-\sin \ | -\sin \theta \\ | ||
\sin \ | \sin \varphi \sin \theta \cos \psi - \cos \varphi \sin \psi & | ||
\sin \ | \sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi & | ||
\sin \ | \sin \varphi \cos \theta \\ | ||
\cos \ | \cos \varphi \sin \theta \cos \psi + \sin \varphi \sin \psi & | ||
\cos \ | \cos \varphi \sin \theta \sin \psi - \sin \varphi \cos \psi & | ||
\cos \ | \cos \varphi \cos \theta | ||
\end{pmatrix} | \end{pmatrix} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Zeile 294: | Zeile 442: | ||
& = | & = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
\ldots & \ldots & - \sin \ | \ldots & \ldots & - \sin \theta \\ | ||
\ldots & \ldots & \sin \ | \ldots & \ldots & \sin \varphi \cos \theta \\ | ||
\ldots & \ldots & \cos \ | \ldots & \ldots & \cos \varphi \cos \theta | ||
\end{pmatrix} | \end{pmatrix} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Zeile 302: | Zeile 450: | ||
0 \\ | 0 \\ | ||
mg | mg | ||
\end{pmatrix} | \end{pmatrix} | ||
= | |||
\begin{pmatrix} | \begin{pmatrix} | ||
-\sin \ | -\sin \theta \\ | ||
\sin \ | \sin \varphi \cos \theta \\ | ||
\cos \ | \cos \varphi \cos \theta | ||
\end{pmatrix} | \end{pmatrix} | ||
mg | mg | ||
| Zeile 313: | Zeile 461: | ||
</math> | </math> | ||
Physikalisch richtig wirkt | Physikalisch richtig wirkt die Gewichtskraft <math>\vec G</math> bei vorhandenem Nickwinkel <math>\theta</math> im Flugzeug beispielsweise auch nach hinten (in negative <math>X</math>-Richtung). | ||
== Matrix-Herleitung im allgemeinen Fall == | == Matrix-Herleitung im allgemeinen Fall == | ||
Für eine beliebige Wahl der Drehachsenreihenfolge kann die sich ergebende Drehmatrix durch die Zuhilfenahme des folgenden Zusammenhangs einfach hergeleitet werden:<ref>Ein ausführlicher Beweis findet sich in: G. Fischer: ''Lernbuch Lineare Algebra und Analytische Geometrie.'' 2. Auflage 2012, in 5.3.6</ref> | Für eine beliebige Wahl der Drehachsenreihenfolge kann die sich ergebende Drehmatrix durch die Zuhilfenahme des folgenden Zusammenhangs einfach hergeleitet werden (aktive Drehungen):<ref>Ein ausführlicher Beweis findet sich in: G. Fischer: ''Lernbuch Lineare Algebra und Analytische Geometrie.'' 2. Auflage 2012, in 5.3.6</ref> | ||
Die Drehmatrizen um die globalen Achsen sind bekannt. Wenn nun um eine bereits gedrehte Achse erneut gedreht werden soll, dann entspricht das der Drehmatrix um die entsprechende globale Achse, allerdings in einer transformierten [[Basis (Vektorraum)|Vektorbasis]]. Die Transformationsmatrix ([[Basiswechselmatrix]]) ist dabei gerade die vorhergehende Drehung. | Die Drehmatrizen um die globalen Achsen sind bekannt. Wenn nun um eine bereits gedrehte Achse erneut gedreht werden soll, dann entspricht das der Drehmatrix um die entsprechende globale Achse, allerdings in einer transformierten [[Basis (Vektorraum)|Vektorbasis]]. Die Transformationsmatrix ([[Basiswechselmatrix]]) ist dabei gerade die vorhergehende Drehung. | ||
Seien <math>A</math> und <math>B</math> zwei Drehmatrizen um die beiden globalen Achsen <math>G</math> und <math>H</math>. Zur Berechnung der Drehmatrix zu der Reihenfolge <math>(G,H^\prime)</math> beobachtet man, dass die Drehmatrix für die zweite Drehung um <math>H</math> der basistransformierten Matrix <math>\tilde B = A B A^{-1}</math> entsprechen muss. Dadurch erhält man für die resultierende Gesamtdrehmatrix <math>C = \tilde B A = A B A^{-1} A = A B</math>. Für eine größere Anzahl von Drehungen erfolgt der Nachweis analog. | Seien <math>A</math> und <math>B</math> zwei Drehmatrizen um die beiden globalen Achsen <math>G</math> und <math>H</math>. Zur Berechnung der Drehmatrix zu der Reihenfolge <math>(G,H^\prime)</math> beobachtet man, dass die Drehmatrix für die zweite Drehung um <math>H</math> der basistransformierten Matrix <math>\tilde B = A B A^{-1}</math> entsprechen muss. Dadurch erhält man für die resultierende Gesamtdrehmatrix <math>C = \tilde B A = A B A^{-1} A = A B</math>. Für eine größere Anzahl von Drehungen erfolgt der Nachweis analog. | ||
Bei drei aktiven Drehungen (A wird zuerst ausgeführt, dann B, dann C) ergibt sich die Gesamtdrehmatrix <math> D = ((AB) \cdot C \cdot {(AB)}^T ) \cdot ( A \cdot B \cdot A^T ) \cdot A = ABC</math> unter Verwendung von <math>A^T = A^{-1}</math>, <math>{(A \cdot B)}^T = B^T \cdot A^T</math>. | |||
Durch diese Darstellung ergibt sich, dass sich die Drehmatrix für eine beliebige Drehreihenfolge in nacheinander gedrehten Achsen durch die einfache Multiplikation von Drehmatrizen um globale Koordinatenachsen ergibt – allerdings in umgekehrter Reihenfolge. | Durch diese Darstellung ergibt sich, dass sich die Drehmatrix für eine beliebige Drehreihenfolge in nacheinander gedrehten Achsen durch die einfache Multiplikation von Drehmatrizen um globale Koordinatenachsen ergibt – allerdings in umgekehrter Reihenfolge. | ||
| Zeile 355: | Zeile 481: | ||
== Mathematische Eigenschaften == | == Mathematische Eigenschaften == | ||
Die Abbildung, die den Euler-Winkeln die zugehörige Drehmatrix zuordnet, besitzt [[Kritischer Punkt (Mathematik)|kritische Punkte]], in denen diese Zuordnung nicht lokal umkehrbar ist und man von | Die Abbildung, die den Euler-Winkeln die zugehörige Drehmatrix zuordnet, besitzt [[Kritischer Punkt (Mathematik)|kritische Punkte]], in denen diese Zuordnung nicht lokal umkehrbar ist und man von einem [[Gimbal Lock]] spricht. Im Fall der og. x- oder y-Konvention tritt dieser stets dann auf, wenn der zweite Rotationswinkel gleich null wird und der [[Axialvektor|Drehvektor]] der ersten Drehung damit derselbe ist wie der Drehvektor der zweiten Drehung. Das aber bedeutet, dass es für eine Rotation um die <math>z</math>-Achse beliebig viele Euler-Winkel mit <math>\alpha = Z+Z'</math> gibt. | ||
Bei der Definition der Lagewinkel nach der Luftfahrtnorm liegen die kritischen Punkte bei <math>\textstyle\theta = \pm \frac{\pi}{2}</math>. | |||
Nach [[Kurt Magnus (Ingenieur)|Kurt Magnus]]<ref>Magnus, Kreisel, Springer, 1971, S. 32</ref> ist bei Kreisel-Problemen, bei denen <math>\theta=0</math> möglich ist, die Beschreibung mit Eulerwinkeln (x-Konvention) nicht möglich und man verwendet stattdessen Kardanwinkel. | |||
== Nachteile, Alternativen == | == Nachteile, Alternativen == | ||
| Zeile 364: | Zeile 492: | ||
* Die korrekte Kombination von Drehungen im Euler-System ist nicht intuitiv anzugeben, da sich die Drehachsen verändern. | * Die korrekte Kombination von Drehungen im Euler-System ist nicht intuitiv anzugeben, da sich die Drehachsen verändern. | ||
Eine andere Möglichkeit, die Orientierung zu beschreiben und teils diese Nachteile zu umgehen, sind [[Quaternionen]]. | Anstatt mit den Eulerwinkeln kann man jede Drehung auch durch einen Vektor angeben, der durch seine Orientierung die Lage der Achse und den Drehsinn angibt, und durch seinen Betrag den Drehwinkel (siehe z. B.<ref>{{Literatur |Autor=Herbert Goldstein, Charles P. Poole, Jr., John L. Safko, Sr. |Titel=Klassische Mechanik |Auflage=3 |Verlag=John Wiley & Sons |Ort= |Datum=2012 |ISBN=978-3-527-40589-3}}</ref> oder [[Orthogonaler Tensor]]). Eine andere Möglichkeit, die Orientierung zu beschreiben und teils diese Nachteile zu umgehen, sind [[Quaternionen]]. | ||
== Anwendungen == | == Anwendungen == | ||
[[Datei:MAUD-MTEX-TiAl-hasylab-2003-Liss.png|mini| | [[Datei:MAUD-MTEX-TiAl-hasylab-2003-Liss.png|mini|links|Textur Polfiguren von gamma-TiAl in einer alpha2-gamma Zweiphasenlegierung.<ref name="Liss">{{cite journal |author=Liss KD, Bartels A, Schreyer A, Clemens H |title=High energy X-rays: A tool for advanced bulk investigations in materials science and physics |journal=Textures Microstruct. |month= |year=2003 |volume=35 |issue=3/4 |pages=219–52 |doi=10.1080/07303300310001634952 }}</ref> ]] | ||
{{Linkbox Lagewinkel|klein}} | {{Linkbox Lagewinkel|klein}} | ||
In der [[Theoretische Physik|Theoretischen Physik]] werden die eulerschen Winkel zur Beschreibung des [[Starrer Körper|Starren Körpers]] benutzt. Eine praktische Anwendung ergibt die bekannte [[kardanische Aufhängung]]<ref>Der Zusammenhang zwischen den eulerschen Winkeln und der kardanischen Aufhängung ist u. a. in Kapitel 11.7 des folgenden Buches dargestellt: U. Krey, A. Owen: ''Basic Theoretical Physics – A Concise Overview.'' Springer-Verlag, Berlin 2007.</ref> der technischen Mechanik. | In der [[Theoretische Physik|Theoretischen Physik]] werden die eulerschen Winkel zur Beschreibung des [[Starrer Körper|Starren Körpers]] benutzt. Eine praktische Anwendung ergibt die bekannte [[kardanische Aufhängung]]<ref>Der Zusammenhang zwischen den eulerschen Winkeln und der kardanischen Aufhängung ist u. a. in Kapitel 11.7 des folgenden Buches dargestellt: U. Krey, A. Owen: ''Basic Theoretical Physics – A Concise Overview.'' Springer-Verlag, Berlin 2007.</ref> der technischen Mechanik. | ||
| Zeile 382: | Zeile 510: | ||
== Literatur == | == Literatur == | ||
* [[Herbert Goldstein]]: ''Klassische Mechanik'', Wiley-VCH 2006 | |||
* Georg Rill, Thomas Schaeffer: ''Grundlagen und Methodik der Mehrkörpersimulation.'' Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-658-16009-8. | * Georg Rill, Thomas Schaeffer: ''Grundlagen und Methodik der Mehrkörpersimulation.'' Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-658-16009-8. | ||
| Zeile 388: | Zeile 517: | ||
{{Wikibooks|Mechanik starrer Körper#Die eulerschen Winkel|''Die Mechanik starrer Körper'', Die eulerschen Winkel}} | {{Wikibooks|Mechanik starrer Körper#Die eulerschen Winkel|''Die Mechanik starrer Körper'', Die eulerschen Winkel}} | ||
* {{MathWorld|id = EulerAngles|title = Euler Angles|author = Eric Weisstein}} | * {{MathWorld|id = EulerAngles|title = Euler Angles|author = Eric Weisstein}} | ||
== Einzelnachweise == | == Einzelnachweise == | ||
<references> | <references> | ||
<ref name="goldstein">{{Literatur|Autor=Herbert Goldstein, Charles P. Poole Jr., John L. Safko|Titel=Klassische Mechanik|Auflage=3., vollständig und erweiterte|Verlag=WILEY-VCH | | <ref name="goldstein"> | ||
{{Literatur |Autor=Herbert Goldstein, Charles P. Poole Jr., John L. Safko |Titel=Klassische Mechanik |Auflage=3., vollständig und erweiterte |Verlag=WILEY-VCH |Datum=2006 |ISBN=3-527-40589-5 |Seiten=161 ff |Online={{Google Buch |BuchID=bbsCZN1U17cC |Seite=161}}}}: „Wir können die Transformation von einem kartesischen Koordinatensystem auf ein anderes mittels dreier aufeinander folgender Drehungen durchführen, die in einer bestimmten Reihenfolge erfolgen müssen.“ | |||
</ref> | </ref> | ||
</references> | </references> | ||
{{Normdaten|TYP=s|GND=4489302-4}} | |||
[[Kategorie:Analytische Geometrie]] | [[Kategorie:Analytische Geometrie]] | ||
Aktuelle Version vom 27. Februar 2022, 12:42 Uhr
Die eulerschen Winkel (oder Euler-Winkel), benannt nach dem Schweizer Mathematiker Leonhard Euler, sind ein Satz von drei Winkeln, mit denen die Orientierung (Drehlage) eines festen Körpers im dreidimensionalen euklidischen Raum beschrieben werden kann.[1] Sie werden üblicherweise mit $ \alpha ,\beta ,\gamma $ oder mit $ \varphi ,\theta ,\psi $ bezeichnet. Der Körper kann zum Beispiel ein Kreisel sein (in der theoretischen Physik) oder ein Fahrzeug, ein Schiff oder ein Flugzeug. In der Astronomie kann der „Körper“ auch die Bahnellipse eines Himmelskörpers sein.
Anstatt der Drehlage eines Körpers können eulersche Winkel auch die Lage eines kartesischen Koordinatensystems in Bezug auf ein anderes kartesisches Koordinatensystem beschreiben und werden deshalb für Koordinatentransformationen verwendet. Oft ist das gedrehte Koordinatensystem an einen gedrehten Körper „angeheftet“. Man spricht dann vom körperfesten Koordinatensystem und nennt das ursprüngliche Koordinatensystem raumfest.
Die Drehlage wird erzeugt, indem der Körper aus seiner Ursprungslage heraus nacheinander um die drei Eulerwinkel um Koordinatenachsen gedreht wird. Für die Wahl der Achsen gibt es verschiedene Konventionen:
- Eigentliche Eulerwinkel: Die erste und die dritte Drehung finden um die gleiche Koordinatenachse statt (z. B. Drehung um z-Achse, x-Achse, z-Achse).
- Kardanwinkel oder Tait-Bryan-Winkel: Alle drei Drehungen werden um verschiedene Koordinatenachsen gedreht (z. B. in der Reihenfolge x-Achse, y-Achse, z-Achse).
Dabei wird entweder bei der zweiten und dritten Drehung um die zuvor gedrehten Koordinatenachsen gedreht (intrinsische Drehungen) oder immer um die ursprünglichen Koordinatenachsen (extrinsische Drehungen).
Die aus den drei Einzeldrehungen zusammengesetzte Drehung kann durch eine Matrix beschrieben werden, die sich entsprechend als Produkt von drei elementaren Drehmatrizen darstellen lässt. Je nach Anwendungszweck betrachtet man verschiedene Matrizen:
- Transformationsmatrix für die Koordinatentransformation vom gedrehten (körperfesten) ins ursprüngliche (raumfeste) Koordinatensystem,
- Transformationsmatrix für die Koordinatentransformation vom raumfesten ins körperfeste Koordinatensystem,
- Abbildungsmatrix der Drehung bezüglich des raumfesten Koordinatensystems.
Geschichte
Drehungen wurden spätestens seit etwa 1600 durch drei Winkel beschrieben. So bestimmte Johannes Kepler in der Astronomia nova die Orientierung der Marsbahn in Bezug auf die Ekliptik durch drei Winkel. Eine algebraische Beschreibung, mit der die Drehlage von beliebigen Punkten berechnet werden konnte, wurde aber erst ab 1775 von Leonhard Euler in zunehmender Tiefe formuliert.[2] In der ersten Arbeit[3] zeigte er, dass die neun, den Elementen der Abbildungsmatrix entsprechenden, Koeffizienten wegen der Längentreue einer Bewegung nicht unabhängig voneinander sind, sondern durch nur drei voneinander unabhängige Winkel festgelegt werden. Es handelt sich bei diesen aber nicht um die hier behandelten eulerschen Winkel, sondern um reine Rechengrößen ohne geometrische Bedeutung. Bekannt ist diese Arbeit heute besonders, weil er in einem Zusatz das heute nach ihm benannte Rotationstheorem bewies, nach dem jede eigentliche Bewegung mit einem Fixpunkt eine Drehung um eine Achse ist. Die aus diesem Ergebnis resultierenden Abbildungsgleichungen, in denen eine Drehung durch die Richtungskosinus der Drehachse und den Drehwinkel parametrisiert wird, fand er in einer kurz darauf folgenden zweiten Arbeit.[4]
In einer dritten, erst postum erschienenen Arbeit[5] führte er schließlich drei Winkel $ p $, $ q $ und $ r $ ein, mit denen er die Transformation von körperfesten in raumfeste Koordinaten beschrieb und die bis auf Vorzeichen und additive Konstanten mit den heute nach ihm benannten Winkeln übereinstimmen. Sein Vorgehen unterschied sich dabei deutlich vom heute gängigen Verfahren, bei dem das eine Koordinatensystem durch drei aufeinanderfolgende Drehungen um die Koordinatenachsen in das andere Koordinatensystem überführt wird. Euler argumentiere ähnlich wie bei der ersten Arbeit, kommt aber zu einem günstigeren Ansatz[5]:S. 50 mit den drei Winkeln $ p $, $ q $ und $ r $, weil er hier – in moderner Sprechweise – nicht nur die Orthonormalität der Zeilen, sondern auch die der Spalten der Transformationsmatrix verwendete. Zur Klärung ihrer geometrischen Bedeutung betrachtete er die Schnittpunkte $ a $, $ b $, $ c $ des raumfesten Koordinatensystems mit der Einheitskugel und die entsprechenden Schnittpunkte $ A $, $ B $, $ C $ des körperfesten Systems und zeigte, dass die Kosinusse der Bögen $ aA $, $ aB $, …, $ cC $ gerade die Koeffizienten der Transformationsgleichungen sind. Es ist also $ p=aA $ der Winkel zwischen der $ x $- und der $ X $-Achse. Außerdem zeigt sich mittels sphärischer Trigonometrie, dass $ q $ der Winkel bei $ A $ im Kugeldreieck $ ABa $ und $ r $ der Winkel bei $ a $ im Kugeldreieck $ abA $ ist. Heute werden die entsprechenden Winkel nicht von der $ xX $-Ebene, sondern von der zu ihr senkrechten Knotenlinie $ N $ aus gemessen; der Zusammenhang mit den heute meist verwendeten Eulerwinkeln für die Drehfolge x-y-x ist gegeben durch $ \alpha =r+90^{\circ } $, $ \beta =p $ und $ \gamma =-q+90^{\circ } $.
Lagrange brachte in der 1788 erschienenen Mécanique Analytique[6] zwei Ableitungen der Transformationsgleichungen. Die erste[6]:S. 381–388 stimmt bis auf die Namen der Winkel (bei ihm heißen sie $ \lambda =p $, $ \mu =r $ und $ \nu =q $) im Wesentlichen mit der von Euler überein. Die zweite[6]:S. 398–401 deckt sich mit der modernen, unten ausführlich behandelten Darstellung für die z-x-z-Drehfolge – wiederum mit anderen Winkelnamen ($ \varphi =\gamma $, $ \psi =\alpha $, $ \omega =\beta $).
Eigentliche Eulerwinkel
Im Folgenden werden wie in der nebenstehenden Grafik die Achsen des Koordinatensystems in Ausgangslage (in der Grafik blau) mit den Kleinbuchstaben $ x $, $ y $ und $ z $, die Achsen in Ziellage (in der Grafik rot) mit den entsprechenden Großbuchstaben $ X $, $ Y $ und $ Z $ bezeichnet.
Geometrische Beschreibung
Die $ x $-$ y $-Ebene und die $ X $-$ Y $-Ebene schneiden sich in einer Geraden $ N $ (Knotenlinie). Diese steht senkrecht auf der $ z $-Achse und auf der $ Z $-Achse.
- Der erste Euler-Winkel $ \alpha $ (auch $ \varphi $) ist der Winkel zwischen der $ x $-Achse und der Geraden $ N $ (gemessen in Richtung der y-Achse).
- Der zweite Euler-Winkel $ \beta $ (auch $ \theta $) ist der Winkel zwischen der $ z $-Achse und der $ Z $-Achse.
- Der dritte Euler-Winkel $ \gamma $ (auch $ \psi $) ist der Winkel zwischen $ N $ und der $ X $-Achse.
Die hier beschriebene Version der eulerschen Winkel, bei der der Winkel $ \alpha $ von der $ x $-Achse aus zur Knotenlinie und der Winkel $ \gamma $ von der Knotenlinie zur $ X $-Achse gemessen wird, nennt man die Standard-x-Konvention. Entsprechend werden bei der Standard-y-Konvention die Winkel von der $ y $-Achse zur Knotenlinie und von der Knotenlinie zur $ Y $-Achse gemessen.
In der Physik wird meist die Standard-x-Konvention verwendet. Statt wie hier mit $ \alpha $, $ \beta $ und $ \gamma $ werden die Winkel meist mit $ \varphi $, $ \theta $ und $ \psi $ bezeichnet.
Beschreibung durch intrinsische Drehungen
Die Drehung $ r $, welche das $ xyz $-System in das $ XYZ $-System dreht, kann in drei Drehungen aufgeteilt werden. Bei der Standard-x-Konvention sind das:
- Zunächst die Drehung $ r_{z}(\alpha ) $ um den Winkel $ \alpha $ um die $ z $-Achse,
- dann die Drehung $ r_{N}(\beta ) $ um den Winkel $ \beta $ um die Knotenlinie $ N $,
- zuletzt die Drehung $ r_{Z}(\gamma ) $ um den Winkel $ \gamma $ um die $ Z $-Achse.
Bei diesen Drehungen entstehen nacheinander neue Koordinatensysteme:
- ursprüngliches Koordinatensystem: $ x $-, $ y $- und $ z $-Achse
- nach der ersten Drehung: $ x' $-, $ y' $- und $ z' $-Achse
- nach der zweiten Drehung: $ x'' $-, $ y'' $- und $ z'' $-Achse
- nach der dritten Drehung: $ x''' $-, $ y''' $- und $ z''' $-Achse (bzw. $ X $-, $ Y $- und $ Z $-Achse)
Die Drehung um $ N $ ist also eine Drehung um die $ x' $-Achse, die Drehung um die $ Z $-Achse eine Drehung um die $ z'' $-Achse. Die Gesamtdrehung $ r $ setzt sich also aus den Drehungen $ r_{z}(\alpha ) $, $ r_{x'}(\beta ) $ und $ r_{z''}(\gamma ) $ zusammen:
- $ r=r_{z''}(\gamma )\circ r_{x'}(\beta )\circ r_{z}(\alpha ) $
Die Reihenfolge der Drehachsen ist also: $ z $-Achse → $ x' $-Achse → $ z'' $-Achse oder kurz $ z $-$ x' $-$ z'' $.
Eine solche Zerlegung in Drehungen, bei denen jeweils um die mitgedrehten Koordinatenachsen gedreht wird, nennt man intrinsische Drehfolge.
Beschreibung durch extrinsische Drehungen
Dieselbe Drehung $ r $ kann auch durch drei Einzeldrehungen um die ursprünglichen Koordinatenachsen beschrieben werden. Dabei bleiben die Winkel gleich, aber die Reihenfolge der Drehungen kehrt sich um, und die Zwischenlagen $ x'y'z' $ und $ x''y''z'' $ sind andere als bei der intrinsischen Drehung: Zuerst wird der Körper um den Winkel $ \gamma $ um die $ z $-Achse gedreht, dann um $ \beta $ um die $ x $-Achse (der Winkel zwischen der $ x $- und $ x'' $-Achse ist derselbe wie der zwischen der $ x $- und der $ x' $-Achse, nämlich $ \gamma $) und zuletzt um den Winkel $ \alpha $ um die $ z $-Achse (dabei wird die $ x $-Achse in die Knotenlinie $ N $ gedreht und der Winkel zwischen $ N $ und der $ X $-Achse ist $ \gamma $). Eine algebraische Begründung findet sich weiter unten im Abschnitt Matrix-Herleitung im allgemeinen Fall. Es ist also
- $ r=r_{z}(\alpha )\circ r_{x}(\beta )\circ r_{z}(\gamma ) $.
Eine solche Drehfolge, bei der immer um die ursprünglichen Koordinatenachsen gedreht wird, heißt extrinsische Drehfolge.
Die Beschreibungen durch intrinsische und durch extrinsische Drehungen sind also äquivalent. Die Beschreibung durch intrinsische Drehungen ist jedoch anschaulicher, während die Beschreibung durch extrinsische Drehungen mathematisch leichter zugänglich ist.
Beschreibung durch Matrizen
Die Drehungen um die Eulerschen Winkel können mit Hilfe von Drehmatrizen, deren Einträge Sinus- und Kosinus-Werte der Euler-Winkel sind, beschrieben werden. Dabei unterscheidet man zwischen Abbildungsmatrizen und Koordinatentransformationsmatrizen. Im Folgenden werden diese Matrizen für die Standard-x-Konvention angegeben. Die Matrizen für die Standard-y-Konvention erhält man analog, indem man statt der elementaren Drehmatrix für die Drehung um die x-Achse die Drehmatrix für die Drehung um die y-Achse verwendet.
Abbildungsmatrix (aktive Drehung)
Bei einer aktiven Drehung (Alibi-Drehung) werden die Punkte und Vektoren des Raums gedreht. Das Koordinatensystem wird festgehalten. Die Drehmatrix $ R $ ist die Abbildungsmatrix dieser Abbildung. Die Koordinaten des gedrehten Vektors $ {\vec {w}}=r({\vec {v}}) $ ergeben sich aus den Koordinaten des ursprünglichen Punkts $ {\vec {v}} $ durch Multiplikation mit der Drehmatrix:
- $ {\begin{pmatrix}w_{x}\\w_{y}\\w_{z}\\\end{pmatrix}}=R{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\\\end{pmatrix}}\,. $
Die Abbildungsmatrizen für Drehungen um die Koordinatenachsen (elementare Drehmatrizen) lauten:
- $ R_{x}(\alpha )={\begin{pmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{pmatrix}},\quad R_{y}(\alpha )={\begin{pmatrix}\cos \alpha &0&\sin \alpha \\0&1&0\\-\sin \alpha &0&\cos \alpha \end{pmatrix}},\quad R_{z}(\alpha )={\begin{pmatrix}\cos \alpha &-\sin \alpha &0\\\sin \alpha &\cos \alpha &0\\0&0&1\end{pmatrix}} $
für die Drehung um den Winkel $ \alpha $ um die $ x $-Achse, die $ y $-Achse und die $ z $-Achse.
Die Drehmatrix der zusammengesetzten Drehung erhält man durch Matrixmultiplikation aus den Matrizen der einzelnen Drehungen. Da die elementaren Drehmatrizen die Drehungen um die ursprünglichen Koordinatenachsen beschreiben, verwendet man die extrinsische Drehfolge
- $ r=r_{z}(\alpha )\circ r_{x}(\beta )\circ r_{z}(\gamma ) $
und erhält die Abbildungsmatrix
- $ {\begin{aligned}R_{zxz}&=R_{z}(\alpha )\,R_{x}(\beta )\,R_{z}(\gamma )\\&={\begin{pmatrix}\cos \alpha &-\sin \alpha &0\\\sin \alpha &\cos \alpha &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}1&0&0\\0&\cos \beta &-\sin \beta \\0&\sin \beta &\cos \beta \end{pmatrix}}{\begin{pmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{pmatrix}}\\&={\begin{pmatrix}\cos \alpha \cos \gamma -\sin \alpha \cos \beta \sin \gamma &-\cos \alpha \sin \gamma -\sin \alpha \cos \beta \cos \gamma &\sin \alpha \sin \beta \\\sin \alpha \cos \gamma +\cos \alpha \cos \beta \sin \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \beta \cos \gamma &-\cos \alpha \sin \beta \\\sin \beta \sin \gamma &\sin \beta \cos \gamma &\cos \beta \end{pmatrix}}\end{aligned}} $
Transformationsmatrix
Transformationsmatrizen beschreiben Koordinatentransformationen vom ursprünglichen (raumfesten) Koordinatensystem ins gedrehte (körperfeste) oder umgekehrt. Die Transformationsmatrix für die Koordinatentransformation vom körperfesten Koordinatensystem ins raumfeste stimmt mit der oben beschriebenen Abbildungsmatrix überein, die Matrix für die umgekehrte Transformation ist die Transponierte dieser Matrix. Hat der Vektor $ {\vec {v}} $ im raumfesten Koordinatensystem die Koordinaten $ v_{x},v_{y},v_{z} $ und im körperfesten die Koordinaten $ v_{X},v_{Y},v_{Z} $, so gilt
- $ {\begin{aligned}{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\end{pmatrix}}&=R_{zxz}{\begin{pmatrix}v_{X}\\v_{Y}\\v_{Z}\end{pmatrix}}\\&=R_{z}(\alpha )\,R_{x}(\beta )\,R_{z}(\gamma ){\begin{pmatrix}v_{X}\\v_{Y}\\v_{Z}\end{pmatrix}}\\&={\begin{pmatrix}\cos \alpha &-\sin \alpha &0\\\sin \alpha &\cos \alpha &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}1&0&0\\0&\cos \beta &-\sin \beta \\0&\sin \beta &\cos \beta \end{pmatrix}}{\begin{pmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}v_{X}\\v_{Y}\\v_{Z}\end{pmatrix}}\\&={\begin{pmatrix}\cos \alpha \cos \gamma -\sin \alpha \cos \beta \sin \gamma &-\cos \alpha \sin \gamma -\sin \alpha \cos \beta \cos \gamma &\sin \alpha \sin \beta \\\sin \alpha \cos \gamma +\cos \alpha \cos \beta \sin \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \beta \cos \gamma &-\cos \alpha \sin \beta \\\sin \beta \sin \gamma &\sin \beta \cos \gamma &\cos \beta \end{pmatrix}}{\begin{pmatrix}v_{X}\\v_{Y}\\v_{Z}\end{pmatrix}}\end{aligned}} $
und
- $ {\begin{aligned}{\begin{pmatrix}v_{X}\\v_{Y}\\v_{Z}\end{pmatrix}}&=R_{zxz}^{T}{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\end{pmatrix}}\\&=R_{z}(\gamma )^{T}\,R_{x}(\beta )^{T}\,R_{z}(\alpha )^{T}{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\end{pmatrix}}\\&={\begin{pmatrix}\cos \gamma &\sin \gamma &0\\-\sin \gamma &\cos \gamma &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}1&0&0\\0&\cos \beta &\sin \beta \\0&-\sin \beta &\cos \beta \end{pmatrix}}{\begin{pmatrix}\cos \alpha &\sin \alpha &0\\-\sin \alpha &\cos \alpha &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\end{pmatrix}}\\&={\begin{pmatrix}\cos \alpha \cos \gamma -\sin \alpha \cos \beta \sin \gamma &\sin \alpha \cos \gamma +\cos \alpha \cos \beta \sin \gamma &\sin \beta \sin \gamma \\-\cos \alpha \sin \gamma -\sin \alpha \cos \beta \cos \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \beta \cos \gamma &\sin \beta \cos \gamma \\\sin \alpha \sin \beta &-\cos \alpha \sin \beta &\cos \beta \end{pmatrix}}{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\end{pmatrix}}.\end{aligned}} $
Konventionen
Es gibt sechs verschiedene Möglichkeiten, die Achsen für eigentliche Eulerwinkel zu wählen. Bei allen ist die erste und die dritte Achse die gleiche. Die sechs Möglichkeiten sind:
- $ z $-$ x' $-$ z'' $ (intrinsisch) bzw. $ z $-$ x $-$ z $ (extrinsisch): Standard-x-Konvention
- $ z $-$ y' $-$ z'' $ (intrinsisch) bzw. $ z $-$ y $-$ z $ (extrinsisch): Standard-y-Konvention
- $ y $-$ z' $-$ y'' $ (intrinsisch) bzw. $ y $-$ z $-$ y $ (extrinsisch)
- $ y $-$ x' $-$ y'' $ (intrinsisch) bzw. $ y $-$ x $-$ y $ (extrinsisch)
- $ x $-$ y' $-$ x'' $ (intrinsisch) bzw. $ x $-$ y $-$ x $ (extrinsisch)
- $ x $-$ z' $-$ x'' $ (intrinsisch) bzw. $ x $-$ z $-$ x $ (extrinsisch)
Kardan-Winkel
Bei den Kardan-Winkeln (nach Gerolamo Cardano) oder auch Tait-Bryan-Winkeln (benannt nach Peter Guthrie Tait und George Hartley Bryan) erfolgen die drei Drehungen um drei verschiedene Achsen. Wie bei den eigentlichen Eulerwinkeln gibt es sechs mögliche Drehfolgen:
- $ z $-$ y' $-$ x'' $ (intrinsisch) bzw. $ x $-$ y $-$ z $ (extrinsisch)
- $ z $-$ x' $-$ y'' $ (intrinsisch) bzw. $ y $-$ x $-$ z $ (extrinsisch)
- $ y $-$ z' $-$ x'' $ (intrinsisch) bzw. $ x $-$ z $-$ y $ (extrinsisch)
- $ y $-$ x' $-$ z'' $ (intrinsisch) bzw. $ z $-$ x $-$ y $ (extrinsisch)
- $ x $-$ y' $-$ z'' $ (intrinsisch) bzw. $ z $-$ y $-$ x $ (extrinsisch)
- $ x $-$ z' $-$ y'' $ (intrinsisch) bzw. $ y $-$ z $-$ x $ (extrinsisch)
Roll-, Nick- und Gierwinkel: z-y′-x″-Konvention
Beschreibung
Die in der Luftfahrt, Schifffahrt und dem Automobilbau angewendeten und genormten (Luftfahrt: DIN 9300; Automobilbau: DIN ISO 8855) Drehfolgen gehören in die Gruppe der Tait-Bryan-Drehungen. In den Normen sind die Namen Gier-, Nick- und Roll-Winkel (engl. yaw, pitch and roll angle) für die drei Euler-Winkel vorgeschrieben. Durch die drei Drehungen wird das erdfeste $ xyz $-System (engl. world frame) in das körperfeste $ XYZ $-Koordinatensystem (engl. body frame) gedreht.
Intrinsische Reihenfolge $ z $-$ y' $-$ x'' $ (Gier-Nick-Roll-Winkel):
- Mit dem im erdfesten System gemessenen Gierwinkel $ \psi $ (auch Steuerkurs oder Azimut genannt) wird um die $ z $-Achse gedreht. Die $ y $-Achse wird zur Knotenachse $ N(y') $.
Hauptwertebereich: $ -\pi <\psi \leq \pi $. Die Drehrichtung ist mathematisch positiv (gegen den Uhrzeigersinn) - Mit dem gegen die Erdoberfläche ($ x $-$ y $-Ebene) gemessenen Nickwinkel $ \theta $ wird um die Knotenachse $ N(y') $ gedreht. Es entsteht die fahrzeugfeste $ X $-Achse.
Hauptwertebereich: $ -{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}} $. Die Drehrichtung ist mathematisch positiv.
- Der Rollwinkel $ \varphi $ (auch Wankwinkel genannt) beschreibt die Drehung um die fahrzeugfeste $ X $-Achse. Es entstehen die fahrzeugfesten Achsen $ Y $ und $ Z $.
Hauptwertebereich: $ -\pi <\varphi \leq \pi $. Die Drehrichtung ist mathematisch positiv.
Extrinsisch entspricht dies der Reihenfolge $ x $-$ y $-$ z $ (Roll-Nick-Gier-Winkel).
Statt der Kleinbuchstaben $ \psi $, $ \theta $ und $ \varphi $ werden auch die entsprechenden Großbuchstaben $ \Psi $, $ \Theta $ und $ \Phi $ verwendet.
Transformationsmatrizen
Die Koordinatentransformation vom körperfesten ins raumfeste Koordinatensystem wird durch die Matrix
- $ {\begin{aligned}R_{GNR}&=R_{z}(\psi )\,R_{y}(\theta )\,R_{x}(\varphi )\\&={\begin{pmatrix}\cos \psi &-\sin \psi &0\\\sin \psi &\cos \psi &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}\cos \theta &0&\sin \theta \\0&1&0\\-\sin \theta &0&\cos \theta \end{pmatrix}}{\begin{pmatrix}1&0&0\\0&\cos \varphi &-\sin \varphi \\0&\sin \varphi &\cos \varphi \end{pmatrix}}\\&={\begin{pmatrix}\cos \theta \cos \psi &\sin \varphi \sin \theta \cos \psi -\cos \varphi \sin \psi &\cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi \\\cos \theta \sin \psi &\sin \varphi \sin \theta \sin \psi +\cos \varphi \cos \psi &\cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi \\-\sin \theta &\sin \varphi \cos \theta &\cos \varphi \cos \theta \end{pmatrix}}\end{aligned}} $
beschrieben. Die umgekehrte Transformation vom raumfesten ins körperfeste Koordinatensystem wird durch die Transponierte dieser Matrix beschrieben. (Eigentlich die Inverse, aber bei Drehmatrizen stimmt die inverse mit der transponierten Matrix überein.)
- $ {\begin{aligned}R_{GNR}^{T}&=R_{x}(\varphi )^{T}\,R_{y}(\theta )^{T}\,R_{z}(\psi )^{T}\\&={\begin{pmatrix}1&0&0\\0&\cos \varphi &\sin \varphi \\0&-\sin \varphi &\cos \varphi \end{pmatrix}}{\begin{pmatrix}\cos \theta &0&-\sin \theta \\0&1&0\\\sin \theta &0&\cos \theta \end{pmatrix}}{\begin{pmatrix}\cos \psi &\sin \psi &0\\-\sin \psi &\cos \psi &0\\0&0&1\end{pmatrix}}\\&={\begin{pmatrix}\cos \theta \cos \psi &\cos \theta \sin \psi &-\sin \theta \\\sin \varphi \sin \theta \cos \psi -\cos \varphi \sin \psi &\sin \varphi \sin \theta \sin \psi +\cos \varphi \cos \psi &\sin \varphi \cos \theta \\\cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi &\cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi &\cos \varphi \cos \theta \end{pmatrix}}\end{aligned}} $
Das bedeutet: Hat der Vektor $ {\vec {v}} $ im raumfesten System die Koordinaten $ v_{x} $, $ v_{y} $, $ v_{z} $ und im körperfesten System die Koordinaten $ v_{X} $, $ v_{Y} $, $ v_{Z} $, so gilt
- $ {\begin{aligned}{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\end{pmatrix}}&={\begin{pmatrix}\cos \psi &-\sin \psi &0\\\sin \psi &\cos \psi &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}\cos \theta &0&\sin \theta \\0&1&0\\-\sin \theta &0&\cos \theta \end{pmatrix}}{\begin{pmatrix}1&0&0\\0&\cos \varphi &-\sin \varphi \\0&\sin \varphi &\cos \varphi \end{pmatrix}}{\begin{pmatrix}v_{X}\\v_{Y}\\v_{Z}\end{pmatrix}}\\&={\begin{pmatrix}\cos \theta \cos \psi &\sin \varphi \sin \theta \cos \psi -\cos \varphi \sin \psi &\cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi \\\cos \theta \sin \psi &\sin \varphi \sin \theta \sin \psi +\cos \varphi \cos \psi &\cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi \\-\sin \theta &\sin \varphi \cos \theta &\cos \varphi \cos \theta \end{pmatrix}}{\begin{pmatrix}v_{X}\\v_{Y}\\v_{Z}\end{pmatrix}}\end{aligned}} $
und
- $ {\begin{aligned}{\begin{pmatrix}v_{X}\\v_{Y}\\v_{Z}\end{pmatrix}}&={\begin{pmatrix}1&0&0\\0&\cos \varphi &\sin \varphi \\0&-\sin \varphi &\cos \varphi \end{pmatrix}}{\begin{pmatrix}\cos \theta &0&-\sin \theta \\0&1&0\\\sin \theta &0&\cos \theta \end{pmatrix}}{\begin{pmatrix}\cos \psi &\sin \psi &0\\-\sin \psi &\cos \psi &0\\0&0&1\end{pmatrix}}{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\end{pmatrix}}\\&={\begin{pmatrix}\cos \theta \cos \psi &\cos \theta \sin \psi &-\sin \theta \\\sin \varphi \sin \theta \cos \psi -\cos \varphi \sin \psi &\sin \varphi \sin \theta \sin \psi +\cos \varphi \cos \psi &\sin \varphi \cos \theta \\\cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi &\cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi &\cos \varphi \cos \theta \end{pmatrix}}{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\end{pmatrix}}\end{aligned}} $
Anwendungsbeispiel
Der Gewichtsvektor $ {\vec {G}} $ hat im erdfesten $ xyz $-Koordinatensystem nur eine $ z $-Komponente (in Richtung Erdmittelpunkt):
- $ {\vec {G}}_{E}={\begin{pmatrix}0\\0\\mg\end{pmatrix}} $
Die Transformation ins flugzeugfeste Koordinatensystem geschieht dann durch Multiplikation des erdfesten Gewichtsvektors $ {\vec {G}}_{E} $ mit der Transformationsmatrix $ R_{GNR}^{T} $:
- $ {\begin{aligned}{\vec {G}}_{F}&=R_{GNR}^{T}\,{\vec {G}}_{E}\\&={\begin{pmatrix}\cos \theta \cos \psi &\cos \theta \sin \psi &-\sin \theta \\\sin \varphi \sin \theta \cos \psi -\cos \varphi \sin \psi &\sin \varphi \sin \theta \sin \psi +\cos \varphi \cos \psi &\sin \varphi \cos \theta \\\cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi &\cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi &\cos \varphi \cos \theta \end{pmatrix}}{\begin{pmatrix}0\\0\\mg\end{pmatrix}}\\&={\begin{pmatrix}\ldots &\ldots &-\sin \theta \\\ldots &\ldots &\sin \varphi \cos \theta \\\ldots &\ldots &\cos \varphi \cos \theta \end{pmatrix}}{\begin{pmatrix}0\\0\\mg\end{pmatrix}}={\begin{pmatrix}-\sin \theta \\\sin \varphi \cos \theta \\\cos \varphi \cos \theta \end{pmatrix}}mg\end{aligned}} $
Physikalisch richtig wirkt die Gewichtskraft $ {\vec {G}} $ bei vorhandenem Nickwinkel $ \theta $ im Flugzeug beispielsweise auch nach hinten (in negative $ X $-Richtung).
Matrix-Herleitung im allgemeinen Fall
Für eine beliebige Wahl der Drehachsenreihenfolge kann die sich ergebende Drehmatrix durch die Zuhilfenahme des folgenden Zusammenhangs einfach hergeleitet werden (aktive Drehungen):[7]
Die Drehmatrizen um die globalen Achsen sind bekannt. Wenn nun um eine bereits gedrehte Achse erneut gedreht werden soll, dann entspricht das der Drehmatrix um die entsprechende globale Achse, allerdings in einer transformierten Vektorbasis. Die Transformationsmatrix (Basiswechselmatrix) ist dabei gerade die vorhergehende Drehung.
Seien $ A $ und $ B $ zwei Drehmatrizen um die beiden globalen Achsen $ G $ und $ H $. Zur Berechnung der Drehmatrix zu der Reihenfolge $ (G,H^{\prime }) $ beobachtet man, dass die Drehmatrix für die zweite Drehung um $ H $ der basistransformierten Matrix $ {\tilde {B}}=ABA^{-1} $ entsprechen muss. Dadurch erhält man für die resultierende Gesamtdrehmatrix $ C={\tilde {B}}A=ABA^{-1}A=AB $. Für eine größere Anzahl von Drehungen erfolgt der Nachweis analog.
Bei drei aktiven Drehungen (A wird zuerst ausgeführt, dann B, dann C) ergibt sich die Gesamtdrehmatrix $ D=((AB)\cdot C\cdot {(AB)}^{T})\cdot (A\cdot B\cdot A^{T})\cdot A=ABC $ unter Verwendung von $ A^{T}=A^{-1} $, $ {(A\cdot B)}^{T}=B^{T}\cdot A^{T} $.
Durch diese Darstellung ergibt sich, dass sich die Drehmatrix für eine beliebige Drehreihenfolge in nacheinander gedrehten Achsen durch die einfache Multiplikation von Drehmatrizen um globale Koordinatenachsen ergibt – allerdings in umgekehrter Reihenfolge.
Ergebnis, Interpretation
Das erhaltene Koordinatensystem mit den Achsen $ X'' $, $ Y'' $ und $ Z'' $ ist das sogenannte körperfeste System. Die Winkel $ \phi $ und $ \theta $ geben dabei die Lage der $ Z'' $-Achse gegenüber dem körperfesten System an („Drehung“ und „Kippung“); der Winkel $ \psi $ beschreibt die Eigendrehung des Körpers um sie. Dem entsprechen folgende Namenskonventionen:
- Flugsteuerung (Rollwinkel, Nickwinkel, Gierwinkel)
- Kreiseltheorie: Präzession, Nutation und Spin oder Eigenrotation
- Azimut, Höhenwinkel oder Elevation und Rotation
Mathematische Eigenschaften
Die Abbildung, die den Euler-Winkeln die zugehörige Drehmatrix zuordnet, besitzt kritische Punkte, in denen diese Zuordnung nicht lokal umkehrbar ist und man von einem Gimbal Lock spricht. Im Fall der og. x- oder y-Konvention tritt dieser stets dann auf, wenn der zweite Rotationswinkel gleich null wird und der Drehvektor der ersten Drehung damit derselbe ist wie der Drehvektor der zweiten Drehung. Das aber bedeutet, dass es für eine Rotation um die $ z $-Achse beliebig viele Euler-Winkel mit $ \alpha =Z+Z' $ gibt.
Bei der Definition der Lagewinkel nach der Luftfahrtnorm liegen die kritischen Punkte bei $ \textstyle \theta =\pm {\frac {\pi }{2}} $.
Nach Kurt Magnus[8] ist bei Kreisel-Problemen, bei denen $ \theta =0 $ möglich ist, die Beschreibung mit Eulerwinkeln (x-Konvention) nicht möglich und man verwendet stattdessen Kardanwinkel.
Nachteile, Alternativen
Zur Darstellung von Drehungen haben Euler-Winkel mehrere Nachteile:
- Die oben erwähnte Singularität führt dazu, dass eine einzige Drehung durch unterschiedliche Euler-Drehungen ausgedrückt werden kann. Dies führt zu einem Phänomen, das als Gimbal Lock bekannt ist.
- Die korrekte Kombination von Drehungen im Euler-System ist nicht intuitiv anzugeben, da sich die Drehachsen verändern.
Anstatt mit den Eulerwinkeln kann man jede Drehung auch durch einen Vektor angeben, der durch seine Orientierung die Lage der Achse und den Drehsinn angibt, und durch seinen Betrag den Drehwinkel (siehe z. B.[9] oder Orthogonaler Tensor). Eine andere Möglichkeit, die Orientierung zu beschreiben und teils diese Nachteile zu umgehen, sind Quaternionen.
Anwendungen

| Roll-Nick-Gier-Winkel (Eulerwinkel) | |
|---|---|
| Rotationsachsen: | Bewegung: |
| ↙ Längsachse (Roll-/Wankachse): | Rollen, Wanken |
| ↖ Querachse (Nickachse): | Nicken, Stampfen |
| ↓ Vertikalachse (Gierachse): | Gieren (Schlingern) |
In der Theoretischen Physik werden die eulerschen Winkel zur Beschreibung des Starren Körpers benutzt. Eine praktische Anwendung ergibt die bekannte kardanische Aufhängung[11] der technischen Mechanik.
Bei Fahrzeugen bezeichnet man die Euler-Winkel der Hauptlagen als Roll-Nick-Gier-Winkel.
In der Kristallographie werden die eulerschen Winkel zur Beschreibung der Kreise des Einkristalldiffraktometers (mit einer kardanischen Aufhängung aus zwei senkrecht aufeinander stehenden Drehkreisen, die den Euler-Winkeln entspricht und Euler-Wiege genannt wird)[12] und zur Beschreibung der Orientierungsdichteverteilungsfunktion von Texturen verwendet.
In der Astronomie sind die eulerschen Winkel unter anderen Bezeichnungen als Bahnelement eines Objekts geläufig.
In der Computergrafik werden die eulerschen Winkel zur Beschreibung der Orientierung eines Objektes verwendet.
In der Festkörper-NMR werden die eulerschen Winkel zur theoretischen Beschreibung und zur Simulation von Spektren benutzt.
Literatur
- Herbert Goldstein: Klassische Mechanik, Wiley-VCH 2006
- Georg Rill, Thomas Schaeffer: Grundlagen und Methodik der Mehrkörpersimulation. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-658-16009-8.
Weblinks
- Eric Weisstein: Euler Angles. In: MathWorld (englisch).
Einzelnachweise
- ↑ Herbert Goldstein, Charles P. Poole Jr., John L. Safko: Klassische Mechanik. 3., vollständig und erweiterte Auflage. WILEY-VCH, 2006, ISBN 3-527-40589-5, S. 161 ff. (eingeschränkte Vorschau in der Google-Buchsuche).: „Wir können die Transformation von einem kartesischen Koordinatensystem auf ein anderes mittels dreier aufeinander folgender Drehungen durchführen, die in einer bestimmten Reihenfolge erfolgen müssen.“
- ↑ Hui Cheng, K. C. Gupta: A Historical Note on Final Rotations. In: Journal of Applied Mechanics. Band 56, Nr. 1, März 1989, S. 139–145, doi:10.1115/1.3176034 (Volltext [PDF; abgerufen am 13. Dezember 2018]).
- ↑ L. Eulerus: Formulae generales pro translatione quacunque corporum rigidorum. In: Novi Commentarii academiae scientiarum Petropolitanae. Band 20 (1775), 1776, S. 189–207 (Online mit englischer Übersetzung [PDF; 188 kB; abgerufen am 13. Dezember 2018] translatio ist hier eine beliebige Bewegung).
- ↑ L. Eulerus: Nova methodus motum corporum rigidorum determinandi. In: Novi Commentarii academiae scientiarum Petropolitanae. Band 20 (1775), 1776, S. 208–238 (Online [PDF; 1,6 MB; abgerufen am 13. Dezember 2018] die Abbildungsgleichungen stehen in §13).
- ↑ 5,0 5,1 5,2 Leonardus Eulerus: De motu corporum circa punctum fixum mobilium. In: Leonardi Euleri opera postuma mathematica et physica : anno MDCCCXLIV detecta. Band 2, 1862, S. 43–62 (Online [PDF; 1,4 MB; abgerufen am 13. Dezember 2018]). – zugehörige Abbildungen
- ↑ 6,0 6,1 6,2 La Grange: Analytische Mechanik. Göttingen 1797 (Scan [PDF; abgerufen am 13. Dezember 2018] Originaltitel: Mécanique Analytique. 1788. Übersetzt von Friedrich Wilhelm August Murhard).
- ↑ Ein ausführlicher Beweis findet sich in: G. Fischer: Lernbuch Lineare Algebra und Analytische Geometrie. 2. Auflage 2012, in 5.3.6
- ↑ Magnus, Kreisel, Springer, 1971, S. 32
- ↑ Herbert Goldstein, Charles P. Poole, Jr., John L. Safko, Sr.: Klassische Mechanik. 3. Auflage. John Wiley & Sons, 2012, ISBN 978-3-527-40589-3.
- ↑ Liss KD, Bartels A, Schreyer A, Clemens H: High energy X-rays: A tool for advanced bulk investigations in materials science and physics. In: Textures Microstruct. 35. Jahrgang, Nr. 3/4, 2003, S. 219–52, doi:10.1080/07303300310001634952.
- ↑ Der Zusammenhang zwischen den eulerschen Winkeln und der kardanischen Aufhängung ist u. a. in Kapitel 11.7 des folgenden Buches dargestellt: U. Krey, A. Owen: Basic Theoretical Physics – A Concise Overview. Springer-Verlag, Berlin 2007.
- ↑ Euler-Wiege, Lexikon der Geowissenschaften, Spektrum