Radiant (Einheit): Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- SI-Einheit
- Winkeleinheit
imported>Zahnputzbecher K (Änderungen von 91.11.94.77 (Diskussion) auf die letzte Version von Alnilam zurückgesetzt) |
imported>BurghardRichter (→Einleitung: Rv: Falsch plazierte Abbildung aus der Infobox entfernt. Die Vorlage:Infobox Physikalische Einheit ermöglicht keine Einbindung einer Abbildung. Sie bietet auch keinen Mehrwert gegenüber der Abbildung, die ohnehin schon unterhalb der Infobox steht.) |
||
| Zeile 11: | Zeile 11: | ||
| SieheAuch = [[Winkelmaß]]e | | SieheAuch = [[Winkelmaß]]e | ||
}} | }} | ||
[[Datei: | [[Datei:Circle radians.gif|mini|Der Winkel, der auf dem Kreisumfang die Länge des Radius markiert, beträgt 1 rad, der Vollwinkel also <math>2\pi</math> rad.]] | ||
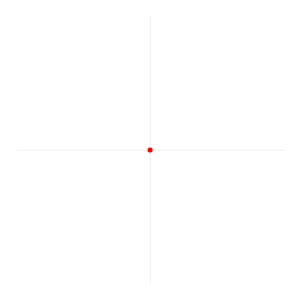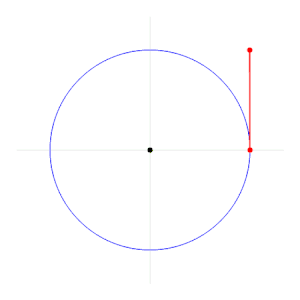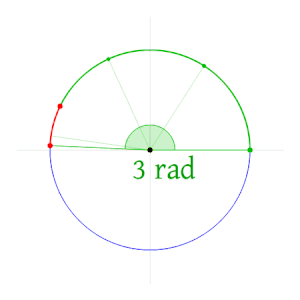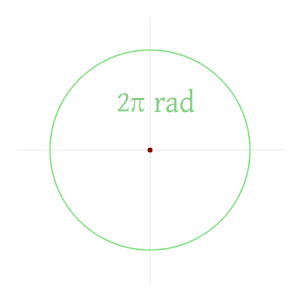
Der '''Radiant''' (Einheitenzeichen: '''rad''') ist ein [[Winkelmaß]], bei dem der Winkel durch die Länge des entsprechenden [[Kreisbogen]]s im [[Einheitskreis]] angegeben wird. Wegen der Betrachtung des Kreisbogens zur Kennzeichnung des Winkels wird die Angabe „'''im Bogenmaß'''“ auch '''Bogenwinkel''' genannt. | Der '''Radiant''' (Einheitenzeichen: '''rad''') ist ein [[Winkelmaß]], bei dem der Winkel durch die Länge des entsprechenden [[Kreisbogen]]s im [[Einheitskreis]] angegeben wird. Wegen der Betrachtung des Kreisbogens zur Kennzeichnung des Winkels wird die Angabe „'''im Bogenmaß'''“ auch '''Bogenwinkel''' genannt. | ||
Die Bogenlänge eines gegebenen Winkels ist proportional dem [[Radius]] <math>r</math>. Auf einem Kreis mit 5 cm Radius markiert ein Winkel von 1 rad also einen 5 cm langen Bogen. Der Vollkreis (360°) hat die Bogenlänge <math>U = 2 \pi r</math>, also beträgt der [[Vollwinkel]] <math>2 \pi</math> rad. | Die Bogenlänge eines gegebenen Winkels ist proportional dem [[Radius]] <math>r</math>. Auf einem Kreis mit 5 cm Radius markiert ein Winkel von 1 rad also einen 5 cm langen Bogen. Der Vollkreis (360°) hat die Bogenlänge <math>U = 2</math>[[Kreiszahl|<math>\pi</math>]]<math>r</math>, also beträgt der [[Vollwinkel]] <math>2 \pi</math> rad. | ||
In vielen Berechnungen der [[Physik]] und der [[Mathematik]] ist das Bogenmaß das zweckmäßigste Winkelmaß, siehe etwa [[Winkelgeschwindigkeit]] und [[Sinus und Kosinus]]. | In vielen Berechnungen der [[Physik]] und der [[Mathematik]] ist das Bogenmaß das zweckmäßigste Winkelmaß, siehe etwa [[Winkelgeschwindigkeit]] und [[Sinus und Kosinus]]. | ||
Im [[Internationales Einheitensystem|Internationalen Einheitensystem]] (SI) ist Radiant der besondere Name für die | Im [[Internationales Einheitensystem|Internationalen Einheitensystem]] (SI) ist Radiant der besondere Name für die [[Internationales Einheitensystem#Kohärente Einheiten|kohärente, abgeleitete SI-Einheit]] m/m mit der [[Größe der Dimension Zahl|Dimension Zahl]]. Er ist also eine [[Hilfsmaßeinheit]] und kann in Rechnungen einfach durch 1 ersetzt werden, d. h. 1 rad = 1. Die Einheit kann mit [[SI-Präfix]]en kombiniert werden, z. B. mrad für ''Milliradiant''.<ref name="SI-Brosch">[https://www.bipm.org/en/publications/si-brochure/ ''Le Système international d’unités''.] 9e édition, 2019 (die sogenannte „SI-Broschüre“, französisch und englisch).</ref> | ||
In der Praxis wird das nachgestellte [[Einheitenkürzel]] ''rad'' häufig dann weggelassen, wenn das Winkelmaß als Vielfaches von <math>\pi</math> angegeben wird, da dann eine Verwechslung mit den Angaben in Winkelgrad ''°'' oder in ''[[gon]]'' unwahrscheinlich ist. | |||
== Umrechnung zwischen Radiant und Grad == | == Umrechnung zwischen Radiant und Grad == | ||
| Zeile 43: | Zeile 45: | ||
|} | |} | ||
Wissenschaftliche Taschenrechner berechnen Winkelfunktionen wahlweise in Grad oder in Radiant, manchmal zusätzlich auch in [[Gon]], wo der Vollwinkel 400 gon umfasst. Die Modi zur Berechnung heißen auf den meisten Taschenrechnern „DEG“ (von {{enS|''degree''}} für Grad) | Wissenschaftliche Taschenrechner berechnen Winkelfunktionen wahlweise in Grad oder in Radiant, manchmal zusätzlich auch in [[Gon]], wo der Vollwinkel 400 gon umfasst. Die Modi zur Berechnung heißen auf den meisten Taschenrechnern „DEG“ (von {{enS|''degree''}} für Grad) für das Gradmaß, „RAD“ für das Bogenmaß und „GRD“, „GRA“ oder „GRAD“ für das Gon-Winkelmaß, und sind manchmal über eine Kombitaste „DRG“ (von den Anfangsbuchstaben der Einheiten) zyklisch umschaltbar. | ||
Winkelfunktionen in mathematischen Bibliotheken für [[Programmiersprache]]n und in Programmen zur Tabellenkalkulation verwenden | Winkelfunktionen in mathematischen Bibliotheken für [[Programmiersprache]]n und in Programmen zur Tabellenkalkulation verwenden in der Regel das Bogenmaß, Gradangaben müssen daher meist umgerechnet werden. Der Vollwinkel hat 2 <math>\pi</math> Radiant oder 360 [[Grad (Winkel)|Grad]], daher gilt: | ||
:<math> | :<math> | ||
| Zeile 69: | Zeile 71: | ||
== Historisches == | == Historisches == | ||
Im SI war zunächst offengelassen worden, ob Radiant und [[Steradiant]] abgeleitete Einheiten oder Basiseinheiten sind; für beide wurde die Klasse der „ergänzenden Einheiten“ geschaffen. 1980 empfahl das [[CIPM]], diese ergänzenden Einheiten als abgeleitete zu interpretieren. Dem folgte 1995 die 20. [[CGPM]] und beschloss | Im SI war zunächst offengelassen worden, ob Radiant und [[Steradiant]] abgeleitete Einheiten oder Basiseinheiten sind; für beide wurde die Klasse der „ergänzenden Einheiten“ geschaffen. 1980 empfahl das [[CIPM]], diese ergänzenden Einheiten als abgeleitete zu interpretieren. Dem folgte 1995 die 20. [[CGPM]] und beschloss die Aufhebung der Klasse der ergänzenden Einheiten.<ref name="CGPM-20-8" /> | ||
= | |||
== Weblinks == | == Weblinks == | ||
{{Commonscat|Radian|Radiant}} | {{Commonscat|Radian|Radiant}} | ||
== Einzelnachweise == | |||
<references> | |||
<ref name="CGPM-20-8"> | |||
{{Internetquelle | |||
|url=https://www.bipm.org/en/committees/cg/cgpm/20-1995/resolution-8 | |||
|titel=Resolution 8 of the 20st CGPM (1995). Elimination of the class of supplementary units in the SI | |||
|werk= | |||
|hrsg=[[Internationales Büro für Maß und Gewicht|Bureau International des Poids et Mesures]] | |||
|datum= | |||
|sprache=en | |||
|abruf=2021-04-12 | |||
}} | |||
</ref> | |||
</references> | |||
{{Navigationsleiste SI-Einheiten}} | |||
[[Kategorie:Winkeleinheit]] | [[Kategorie:Winkeleinheit]] | ||
Aktuelle Version vom 16. September 2021, 19:03 Uhr
| Physikalische Einheit | |
|---|---|
| Einheitenname | Radiant
|
| Einheitenzeichen | $ \mathrm {rad} $ |
| Physikalische Größe(n) | Ebener Winkel |
| Formelzeichen | $ \alpha ,\beta ,\gamma ... $ |
| Dimension | $ {\mathsf {{\frac {L}{L}}=1}} $ |
| System | Internationales Einheitensystem |
| In SI-Einheiten | $ \mathrm {1\,rad=1\,{\frac {1\;m}{1\;m}}=1} $ |
| Benannt nach | lateinisch radius, „Strahl“ |
| Siehe auch: Winkelmaße | |
Der Radiant (Einheitenzeichen: rad) ist ein Winkelmaß, bei dem der Winkel durch die Länge des entsprechenden Kreisbogens im Einheitskreis angegeben wird. Wegen der Betrachtung des Kreisbogens zur Kennzeichnung des Winkels wird die Angabe „im Bogenmaß“ auch Bogenwinkel genannt. Die Bogenlänge eines gegebenen Winkels ist proportional dem Radius $ r $. Auf einem Kreis mit 5 cm Radius markiert ein Winkel von 1 rad also einen 5 cm langen Bogen. Der Vollkreis (360°) hat die Bogenlänge $ U=2 $$ \pi $$ r $, also beträgt der Vollwinkel $ 2\pi $ rad.
In vielen Berechnungen der Physik und der Mathematik ist das Bogenmaß das zweckmäßigste Winkelmaß, siehe etwa Winkelgeschwindigkeit und Sinus und Kosinus.
Im Internationalen Einheitensystem (SI) ist Radiant der besondere Name für die kohärente, abgeleitete SI-Einheit m/m mit der Dimension Zahl. Er ist also eine Hilfsmaßeinheit und kann in Rechnungen einfach durch 1 ersetzt werden, d. h. 1 rad = 1. Die Einheit kann mit SI-Präfixen kombiniert werden, z. B. mrad für Milliradiant.[1]
In der Praxis wird das nachgestellte Einheitenkürzel rad häufig dann weggelassen, wenn das Winkelmaß als Vielfaches von $ \pi $ angegeben wird, da dann eine Verwechslung mit den Angaben in Winkelgrad ° oder in gon unwahrscheinlich ist.
Umrechnung zwischen Radiant und Grad
| Grad | Radiant |
|---|---|
| $ 180^{\circ } $ | $ \pi \approx 3{,}1416 $ |
| $ 90^{\circ } $ | $ {\frac {1}{2}}\pi \approx 1{,}5708 $ |
| $ 45^{\circ } $ | $ {\frac {1}{4}}\pi \approx 0{,}7854 $ |
| $ 57^{\circ }\,17'\,45'' $ | $ \approx 1 $ |
| $ 57{,}29577951^{\circ } $ | |
| $ 1^{\circ } $ | $ {\frac {\pi }{180}}\approx 17{,}45\,{\text{mrad}} $ |
| $ 3{,}44' $ | $ 1\,{\text{mrad}}=0{,}001 $ |
| $ 1'' $ | $ 4{,}85\,\mu {\text{rad}} $ |
Wissenschaftliche Taschenrechner berechnen Winkelfunktionen wahlweise in Grad oder in Radiant, manchmal zusätzlich auch in Gon, wo der Vollwinkel 400 gon umfasst. Die Modi zur Berechnung heißen auf den meisten Taschenrechnern „DEG“ (von englisch degree für Grad) für das Gradmaß, „RAD“ für das Bogenmaß und „GRD“, „GRA“ oder „GRAD“ für das Gon-Winkelmaß, und sind manchmal über eine Kombitaste „DRG“ (von den Anfangsbuchstaben der Einheiten) zyklisch umschaltbar.
Winkelfunktionen in mathematischen Bibliotheken für Programmiersprachen und in Programmen zur Tabellenkalkulation verwenden in der Regel das Bogenmaß, Gradangaben müssen daher meist umgerechnet werden. Der Vollwinkel hat 2 $ \pi $ Radiant oder 360 Grad, daher gilt:
- $ 2\pi \,\mathrm {rad} =360^{\circ } $
- $ 1\,\mathrm {rad} ={\frac {360^{\circ }}{2\pi }}={\frac {180^{\circ }}{\pi }}\approx 57{,}29577951^{\circ } $
oder:
- $ 1^{\circ }={\frac {2\pi }{360}}\,\mathrm {rad} ={\frac {\pi }{180}}\,\mathrm {rad} \approx 0{,}017453293\,\mathrm {rad} $
Der Faktor für die Umrechnung von Radiant auf Grad ist also $ {\frac {180^{\circ }}{\pi }}\ \left(=1\,\mathrm {rad} =1\right) $
Beispiele:
- $ \alpha ={\frac {3}{2}}\,\pi \,\mathrm {rad} ={\frac {3}{2}}\,\pi \cdot {\frac {180^{\circ }}{\pi }}={\frac {3}{2}}\cdot 180^{\circ }=270^{\circ } $
- $ \beta =45^{\circ }=45^{\circ }\cdot {\frac {\pi }{\displaystyle 180^{\circ }}}={\frac {\pi }{4}}={\frac {\pi }{4}}\,\mathrm {rad} $
Historisches
Im SI war zunächst offengelassen worden, ob Radiant und Steradiant abgeleitete Einheiten oder Basiseinheiten sind; für beide wurde die Klasse der „ergänzenden Einheiten“ geschaffen. 1980 empfahl das CIPM, diese ergänzenden Einheiten als abgeleitete zu interpretieren. Dem folgte 1995 die 20. CGPM und beschloss die Aufhebung der Klasse der ergänzenden Einheiten.[2]
Weblinks
Einzelnachweise
- ↑ Le Système international d’unités. 9e édition, 2019 (die sogenannte „SI-Broschüre“, französisch und englisch).
- ↑ Resolution 8 of the 20st CGPM (1995). Elimination of the class of supplementary units in the SI. Bureau International des Poids et Mesures, abgerufen am 12. April 2021 (Lua-Fehler in Modul:Multilingual, Zeile 149: attempt to index field 'data' (a nil value)).
Vorlage:Navigationsleiste SI-Einheiten