Punktspreizfunktion: Unterschied zwischen den Versionen
- Wikipedia:Vorlagenfehler/Vorlage:Cite journal/Parameter language fehlt
- Wikipedia:Qualitätssicherung Physik
- Wikipedia:Überarbeiten
- Hochfrequenztechnik
- Optik
imported>Crazy1880 (Vorlagen-fix (Parameter:JSTOR)) |
imported>Biggerj1 |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:MultiPhotonExcitation-Fig7-doi10.1186slash1475-925X-5-36.JPEG|mini|Vergleich von berechneten Punktspreizfunktionen bei normaler (Weitfeld-) [[Fluoreszenzmikroskop]]ie, [[Multiphotonenmikroskop|Zwei-Photonen-Mikroskopie]] und [[Konfokalmikroskop|konfokaler Mikroskopie]], oben in der Fokusebene und unten entlang der optischen Achse.]] | {{QS-Physik}} | ||
[[Datei:Convolution Illustrated eng.png|thumb|right|270x270px|Wie ein Bild in einem [[Konfokale Mikroskopie|konfokalen Mikroskop]] gebildet wird: Das Bild entsteht durch [[Faltung (Mathematik)]] der echten Lichtquellen mit der Punktspreizfunktion]] | |||
[[Datei:MultiPhotonExcitation-Fig7-doi10.1186slash1475-925X-5-36.JPEG|mini|Vergleich von berechneten Punktspreizfunktionen bei normaler (Weitfeld-)[[Fluoreszenzmikroskop]]ie, [[Multiphotonenmikroskop|Zwei-Photonen-Mikroskopie]] und [[Konfokalmikroskop|konfokaler Mikroskopie]], oben in der Fokusebene und unten entlang der optischen Achse.]] | |||
Die '''Punktantwort''', '''Punktbildfunktion''', '''Punktverteilungsfunktion''', '''Punktbildverwaschungsfunktion''' oder '''Punktspreizfunktion''' (engl. „point spread function“, kurz '''PSF''') beschreibt in der [[Hochfrequenztechnik]], [[Optik]] und [[Bildverarbeitung]] die Wirkung von bandbegrenzenden Einflussfaktoren wie: | Die '''Punktantwort''', '''Punktbildfunktion''', '''Punktverteilungsfunktion''', '''Punktbildverwaschungsfunktion''' oder '''Punktspreizfunktion''' (engl. „point spread function“, kurz '''PSF''') beschreibt in der [[Hochfrequenztechnik]], [[Optik]] und [[Bildverarbeitung]] die Wirkung von bandbegrenzenden Einflussfaktoren wie: | ||
| Zeile 8: | Zeile 10: | ||
In der [[Lichtmikroskopie]] kann die durch [[Beugung (Physik)|Beugung]] begrenzte, maximal erreichbare [[Auflösung (Physik)|Auflösung]] eines [[Objektiv (Optik)|Objektivs]] mit Hilfe der PSF bestimmt werden. Als Auflösung eines Mikroskops wird in der Regel der Abstand verstanden, den zwei punktförmige Strukturen haben müssen, damit sie als getrennte Strukturen (und nicht als eine Struktur) erkannt werden können. | In der [[Lichtmikroskopie]] kann die durch [[Beugung (Physik)|Beugung]] begrenzte, maximal erreichbare [[Auflösung (Physik)|Auflösung]] eines [[Objektiv (Optik)|Objektivs]] mit Hilfe der PSF bestimmt werden. Als Auflösung eines Mikroskops wird in der Regel der Abstand verstanden, den zwei punktförmige Strukturen haben müssen, damit sie als getrennte Strukturen (und nicht als eine Struktur) erkannt werden können. | ||
Während die Breite (FWHM) der Punktspreizfunktion den wichtigsten Faktor für die Auflösung darstellt, hängt die tatsächlich erreichte Auflösung eines mikroskopischen Bilds auch noch von anderen Faktoren wie dem [[Signal-Rausch-Verhältnis]] ab. | |||
Mikroskopisch aufgenommen wird jedoch meist nur das Bild einer kleinen kugelförmigen Struktur, also beispielsweise das mikroskopische Abbild von sehr kleinen [[Fluoreszenz|fluoreszierenden]] Latexkügelchen<ref>{{cite journal |author=Nasse M. J., Woehl J. C., Huant S. |title=High-resolution mapping of the three-dimensional point spread function in the near-focus region of a confocal microscope |journal=Appl. Phys. Lett. |volume=90 |issue=031106 |pages=031106-1-3 |year=2007 |doi=10.1063/1.2431764 }}</ref>. Um ein Maß für die erreichbare Auflösung in der x-, y- | == Bestimmung == | ||
{{cite journal |author=Nasse M. J., Woehl J. C. |title=Realistic modeling of the illumination point spread function in confocal scanning optical microscopy |journal=J. Opt. Soc. Am. A |volume=27 |issue=2 |pages=295–302 |year=2010 |doi=10.1364/JOSAA.27.000295 }}</ref>. | === Experimentelle Messung=== | ||
Mikroskopisch aufgenommen wird jedoch meist nur das Bild einer kleinen kugelförmigen Struktur, also beispielsweise das mikroskopische Abbild von sehr kleinen [[Fluoreszenz|fluoreszierenden]] Latexkügelchen<ref>{{cite journal |author=Nasse M. J., Woehl J. C., Huant S. |title=High-resolution mapping of the three-dimensional point spread function in the near-focus region of a confocal microscope |journal=Appl. Phys. Lett. |volume=90 |issue=031106 |pages=031106-1-3 |year=2007 |doi=10.1063/1.2431764 }}</ref>. Um ein Maß für die erreichbare Auflösung in der x-, y- oder z-Richtung zu bestimmen, wird zunächst die Helligkeitsverteilung entlang eines Profils durch den hellsten Punkt parallel zur gewünschten Achse bestimmt. Die Breite dieser Helligkeitsverteilung auf halber Höhe zwischen Intensitätsmaximum und Intensitätsminimum (FWHM ''Full Width Half Maximum'', deutsch [[Halbwertsbreite]]) wird praktischerweise oft als erreichbare Auflösung angegeben. | |||
===Theoretische Berechnung=== | |||
{{Überarbeiten|Details fehlen völlig}} | |||
Alternativ kann die Punktspreizfunktion auch theoretisch für verschiedene experimentelle Abbildungsszenarien berechnet werden<ref>{{Literatur |Autor=B. Richards, E. Wolf |Titel=Electromagnetic diffraction in optical systems II. Structure of the image field in an aplanatic system |Sammelwerk=Proc. R. Soc. Lond. A |Band=Vol. 253 |Datum=1959 |Seiten=358–379 |JSTOR=100740}}</ref><ref>{{cite journal |author=Nasse M. J., Woehl J. C. |title=Realistic modeling of the illumination point spread function in confocal scanning optical microscopy |journal=J. Opt. Soc. Am. A |volume=27 |issue=2 |pages=295–302 |year=2010 |doi=10.1364/JOSAA.27.000295 }}</ref>. | |||
Die Punktspreizfunktion kann mithilfe von [[Beugungsintegral]]en berechnet werden<ref>{{Cite book|url=https://books.google.com/books?id=lCm9Q18P8cMC&newbks=0&printsec=frontcover&pg=PA355&dq=diffraction+integral+point+spread+function&q=diffraction+integral+point+spread+function&hl=de|title=Progress in Optics|date=2008-01-25|publisher=Elsevier|isbn=978-0-08-055768-7|language=en|pages=355}}</ref>. | |||
Das [[Airy-Scheibchen]] ist die Punktspreizfunktion einer Blende, welche zum Beispiel auch die runde Einfassung einer Linse sein kann. | |||
== Siehe auch == | == Siehe auch == | ||
| Zeile 18: | Zeile 26: | ||
* [[Impulsantwort]] | * [[Impulsantwort]] | ||
* [[Modulationsübertragungsfunktion]] | * [[Modulationsübertragungsfunktion]] | ||
* [[Dekonvolution]] | |||
== Weblinks == | == Weblinks == | ||
Aktuelle Version vom 14. November 2021, 12:48 Uhr
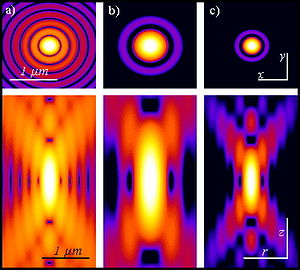
Die Punktantwort, Punktbildfunktion, Punktverteilungsfunktion, Punktbildverwaschungsfunktion oder Punktspreizfunktion (engl. „point spread function“, kurz PSF) beschreibt in der Hochfrequenztechnik, Optik und Bildverarbeitung die Wirkung von bandbegrenzenden Einflussfaktoren wie:
- Beugungserscheinungen an Blenden
- Abbildungsfehler
- Einfluss der Sensorfläche bzw. Apertur
Sie gibt an, wie ein idealisiertes, punktförmiges Objekt durch ein System abgebildet würde. Oft ist die Form der Punktantwort unabhängig vom ursprünglichen Ort des idealen, punktförmigen Objekts. In diesem Fall spricht man von einem linearen System und die Gesamtantwort des Systems kann als Summe über die Punktantworten des in seine Punkte zerlegten Objektes berechnet werden.
In der Lichtmikroskopie kann die durch Beugung begrenzte, maximal erreichbare Auflösung eines Objektivs mit Hilfe der PSF bestimmt werden. Als Auflösung eines Mikroskops wird in der Regel der Abstand verstanden, den zwei punktförmige Strukturen haben müssen, damit sie als getrennte Strukturen (und nicht als eine Struktur) erkannt werden können. Während die Breite (FWHM) der Punktspreizfunktion den wichtigsten Faktor für die Auflösung darstellt, hängt die tatsächlich erreichte Auflösung eines mikroskopischen Bilds auch noch von anderen Faktoren wie dem Signal-Rausch-Verhältnis ab.
Bestimmung
Experimentelle Messung
Mikroskopisch aufgenommen wird jedoch meist nur das Bild einer kleinen kugelförmigen Struktur, also beispielsweise das mikroskopische Abbild von sehr kleinen fluoreszierenden Latexkügelchen[1]. Um ein Maß für die erreichbare Auflösung in der x-, y- oder z-Richtung zu bestimmen, wird zunächst die Helligkeitsverteilung entlang eines Profils durch den hellsten Punkt parallel zur gewünschten Achse bestimmt. Die Breite dieser Helligkeitsverteilung auf halber Höhe zwischen Intensitätsmaximum und Intensitätsminimum (FWHM Full Width Half Maximum, deutsch Halbwertsbreite) wird praktischerweise oft als erreichbare Auflösung angegeben.
Theoretische Berechnung
Alternativ kann die Punktspreizfunktion auch theoretisch für verschiedene experimentelle Abbildungsszenarien berechnet werden[2][3]. Die Punktspreizfunktion kann mithilfe von Beugungsintegralen berechnet werden[4].
Das Airy-Scheibchen ist die Punktspreizfunktion einer Blende, welche zum Beispiel auch die runde Einfassung einer Linse sein kann.
Siehe auch
- Faltung (Mathematik) Aufbau eines Bildes durch Summierung der Punktantworten des zerlegten Objekts entspricht mathematisch einer Faltung
- Impulsantwort
- Modulationsübertragungsfunktion
- Dekonvolution
Weblinks
- PSF Generator Kostenloses Programm zur Berechnung von Punktspreizfunktionen an der École polytechnique fédérale de Lausanne (auf englisch)
- Non-stationary Correction of Optical Aberrations Paper, in dem PSF zur Korrektur von Abbildungsfehlern in Objektiven verwendet werden.
Einzelnachweise
- ↑ Nasse M. J., Woehl J. C., Huant S.: High-resolution mapping of the three-dimensional point spread function in the near-focus region of a confocal microscope. In: Appl. Phys. Lett. 90. Jahrgang, Nr. 031106, 2007, S. 031106-1–3, doi:10.1063/1.2431764.
- ↑ B. Richards, E. Wolf: Electromagnetic diffraction in optical systems II. Structure of the image field in an aplanatic system. In: Proc. R. Soc. Lond. A. Vol. 253, 1959, S. 358–379, JSTOR:100740.
- ↑ Nasse M. J., Woehl J. C.: Realistic modeling of the illumination point spread function in confocal scanning optical microscopy. In: J. Opt. Soc. Am. A. 27. Jahrgang, Nr. 2, 2010, S. 295–302, doi:10.1364/JOSAA.27.000295.
- ↑ Progress in Optics. (en). Elsevier, 25. Januar 2008, ISBN 978-0-08-055768-7, S. 355.
