Freiheitsgrad

Der Freiheitsgrad $f$ bezeichnet im engen, mechanischen Sinn die Zahl der voneinander unabhängigen (und in diesem Sinne „frei wählbaren“) Bewegungsmöglichkeiten; im weiteren Sinne jeder unabhängige veränderliche innere oder äußere Parameter eines Systems.^[1] Das System muss dabei folgende Eigenschaften haben:

• Es ist durch die Spezifizierung der Parameter eindeutig bestimmt.
• Wird ein Parameter weggelassen, so ist das System nicht mehr eindeutig bestimmt.
• Jeder Parameter kann verändert werden, ohne dass sich die anderen Parameter verändern.

Bei kinematischen Ketten wird der Freiheitsgrad auch Laufgrad genannt.^[2] Die einzelnen Bewegungsmöglichkeiten werden auch Freiheiten genannt. Ein starrer Körper im Raum hat demnach den Freiheitsgrad $f=6$, denn man kann den Körper in drei voneinander unabhängige Richtungen bewegen (Translation) und um drei voneinander unabhängige Achsen drehen (Rotation).

In einem etwas anderen Sprachgebrauch wird jede der unabhängigen Bewegungsmöglichkeiten eines Systems, also jede der genannten Freiheiten, als ein Freiheitsgrad bezeichnet.^[3] In diesem Sinne hat ein starrer Körper ohne Bindungen drei Translationsfreiheitsgrade und drei Rotationsfreiheitsgrade.

Mechanik

Jeder Freiheitsgrad eines physikalischen Systems entspricht einer unabhängigen verallgemeinerten Koordinate, mit der das System beschrieben werden kann.

Was mit dem Wort „unabhängig“ gemeint ist, sieht man an einem Beispiel: Angenommen, ein Teilchen befindet sich in einer Ebene (z. B. auf einem Tisch) mit einem Koordinatensystem und kann sich in dieser Ebene nur entlang einer „schrägen“ Geraden bewegen. Die Position des Teilchens kann dann durch eine einzige Zahl beschrieben werden. Es gibt dafür zwar verschiedene Möglichkeiten, z. B.

• die x-Koordinate des Teilchens (über die Geradengleichung lässt sich daraus dann auch y-Koordinate eindeutig berechnen),
• die y-Koordinate (daraus lässt sich umgekehrt die x-Koordinate berechnen),
• die Winkel-Koordinate in einem polaren Koordinatensystem
• oder den Abstand von einem vorgegebenen festen Punkt auf der Geraden.

In jedem dieser Fälle reicht jedoch stets die Angabe eines einzelnen Werts zur Festlegung der Position. Das Teilchen besitzt daher also nur einen Freiheitsgrad.

Die Zahl der verallgemeinerten Koordinaten ist eine Systemeigenschaft. Beispielsweise hat ein freier Massenpunkt im Raum drei Translationsfreiheitsgrade, die seine Position festlegen. Da ein Punkt keine Ausdehnung hat er jedoch keine Orientierung. Ein starrer Körper besitzt demgegenüber zusätzlich noch drei Rotationsfreiheitsgrade, jeweils beschreibbar durch Drehwinkel.

Gemäß der Grüblerschen Gleichung ist die Zahl der Freiheiten eines Systems, das aus vielen Teilsystemen gebildet wird, gleich der Summe der Freiheiten der Teilsysteme, sofern diese nicht durch Zwangsbedingungen eingeschränkt wird (z. B. Anhängerkupplung: Der Anhänger kann sich nicht vollständig unabhängig vom Zugfahrzeug bewegen).

Ein Doppelpendel, das sich in einer Ebene bewegt. Das System hat zwei Freiheitsgrade, weil sein Zustand mittels der zwei Drehwinkel ${\theta }_1$ und ${\theta }_2$ vollständig beschreibbar ist. Der Massenpunkt $m_1$ hat, für sich betrachtet, den Freiheitsgrad $f=1$, weil seine momentane Position schon über den einzelnen Drehwinkel ${\theta }_1$ festgelegt ist.

Grundsätzlich lassen sich folgende Fälle unterscheiden:

• Für $f\ge 1$ kann sich das System bewegen (Mechanismus)
  • Für $f>1$ ist das System in sich beweglich, d. h. die Bewegungen mehrerer Elemente müssen vorgegeben werden (z. B. mehrere Antriebe), damit die Bewegungen aller Elemente definiert sind.
  • Für $f=1$ liegt „Zwanglauf“ vor. Gibt man die Bewegung eines Elementes vor (z. B. ein Antrieb), sind auch die Bewegungen aller restlichen Elemente definiert. Beispiele: Ein Punkt bewegt sich entlang einer Linie. In einem (idealisierten) Zahnradgetriebe bewirkt die Drehung eines Zahnrads stets eine genau definierte Bewegung aller anderen Zahnräder.
  • Bei $f=2$ können sich z. B. zwei Punkte eines Systems unabhängig voneinander jeweils entlang einer Linie bewegen, ein einzelner Punkt kann sich in einer Ebene bewegen, oder in einem Getriebe ist neben der Drehbewegung eine weitere Bewegung möglich, etwa wenn es sich in einen zweiten Gang schalten lässt.
• Für $f\le 0$ kann sich das System nicht bewegen
  • Für $f=0$ liegt ein statisch bestimmtes System vor, das nur genau eine Position einnehmen kann.
  • Für $f<0$ liegt ein statisch überbestimmtes System vor, in dem starke innere Spannungen auftreten können (es „klemmt“). Dies kann durch Zusatzbedingungen ggf. behoben werden.

Beispiel: Doppelpendel

Zwei freie Punktmassen $m_1$ und $m_2$ haben im dreidimensionalen Raum jeweils drei Translationsfreiheitsgrade, insgesamt also sechs. Ein Doppelpendel, das über Drehgelenke (und nicht über Kugelgelenke) verbunden ist, kann jedoch nur in einer Ebene schwingen, so dass seine Beweglichkeit durch folgende Zwangsbedingungen eingeschränkt ist (s. Abb.):

• $m_1$ befindet sich in der $xy-$Ebene ($z_1=0$), $m_2$ ebenso ($z_2=0$).
• Die Stäbe der beiden Pendel sind starr ($L_1=\mathrm{const}.$ und $L_2=\text{const.}$). Jede Punktmasse kann sich daher nur auf einem Kreisbogen rund um den Kreismittelpunkt bewegen.

Diese vier Zwangsbedingungen reduzieren die Zahl der Freiheitsgrade auf $f=6-4=2$. Für die Beschreibung des Systems genügen daher die beiden Winkel ${\theta }_1$ und ${\theta }_2$ als unabhängige verallgemeinerte Koordinaten.

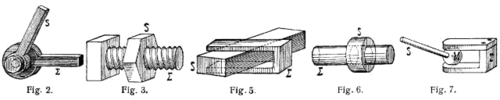
Beispiel: Gelenke

Im Gelenk eines Mechanismus sind zwei Teile miteinander beweglich verbunden. Der Freiheitsgrad $f$ ist die Anzahl der möglichen Bewegungen, die das Gelenk ausführen kann. Dafür stehen prinzipiell die sechs Freiheiten des starren Körpers zur Verfügung. Mindestens eine davon wird im Gelenk unterbunden, daher stehen maximal fünf für eine technische Anwendung zur Verfügung. Mehr als drei Freiheiten werden mit Mehrfachgelenken erreicht.

Verschiedene Gelenke; jeweiliger Freiheitsgrad: siehe links stehende Liste

Thermodynamik und statistische Mechanik

Freiheitsgrade der Moleküle

Komplexe Moleküle besitzen sehr viele Freiheitsgrade

Jedes Molekül mit $n$ Atomen hat allgemein

$f=3n$

Freiheitsgrade, weil man für jedes Atom drei Koordinaten braucht, um seine Position zu definieren. Diese kann man formal in Translations-, Rotations- und innere Schwingungsfreiheitsgrade einteilen:

$\begin{array}{rl}f& =f_{\mathrm{trans}}+f_{\mathrm{rot}}+f_{\mathrm{vib}}\\ \Rightarrow f_{\mathrm{vib}}& =3n-f_{\mathrm{trans}}-f_{\mathrm{rot}}\end{array}$

Für $n$-atomige Moleküle gilt:

Komplexe Moleküle mit vielen Atomen haben daher viele Schwingungsfreiheitsgrade (siehe Molekülschwingung) und liefern somit einen hohen Beitrag zur Entropie.

Bei Molekülen, die auf Festkörperoberflächen adsorbiert sind, kann die Anzahl an Freiheitsgrade reduziert sein. Beispielsweise kann statt drei Rotationsfreiheitsgraden eines Moleküls in der Gasphase für das adsorbierte Molekül nur einer möglich sein. Gleiches gilt für Translationsfreiheitsgrade, die z. B. von drei (Gasphase) zu nur zwei im Fall der Adsorption werden können. Aufgrund der diskreten Energieniveaus der Quantenmechanik können bei niedrigen Energien meist nicht alle $f$ Freiheitsgrade angeregt werden, da der erste angeregte Zustand bereits eine zu hohe Energie besitzt. Dadurch kann ein System bei einer gegebenen Energie effektiv weniger Freiheitsgrade haben:

$f_{\mathrm{eff}}\le f$

Zum Beispiel hat ein Atom bei Raumtemperatur effektiv nur die drei Translationsfreiheitsgrade, da die mittlere Energie so niedrig ist, dass atomare Anregungen praktisch nicht vorkommen.

Das Konzept der Freiheitsgrade aus der Mechanik taucht auch in der statistischen Mechanik und Thermodynamik auf: die Energie eines thermodynamischen Systems verteilt sich gemäß dem Äquipartitionstheorem gleichmäßig auf die einzelnen Freiheitsgrade. Die Zahl der Freiheitsgrade geht in die Entropie ein, die ein Maß für die Zahl der erreichbaren Zustände ist. Thermodynamische Systeme haben generell sehr viele Freiheitsgrade, etwa in der Größenordnung von 10²³, der Größenordnung der Avogadro-Konstanten, da sie üblicherweise Stoffmengen in der Größenordnung eines Mols enthalten. Es können allerdings viele gleichartige Systeme mit jeweils nur wenigen Freiheitsgraden zustande kommen, z. B. 10²³ Atome mit effektiv (s. u.) je drei Freiheitsgraden.

Man kann die innere Energie $U$ eines idealen Gases mit $N$ Teilchen in Abhängigkeit von der Temperatur $T$ und der Anzahl $f_U$ der Freiheitsgrade eines Gasteilchens angeben:

$U=N\cdot \frac{f_U}{2}\cdot k_{\mathrm{B}}\cdot T$

mit der Boltzmann-Konstante $k_{\mathrm{B}}$.

Hierbei ist wichtig, dass Schwingungen bei der Bestimmung von $f_U$ doppelt gezählt werden, da sie sowohl kinetische als auch potentielle Energie besitzen (s. u.):

$f_U=f_{\mathrm{trans}}+f_{\mathrm{rot}}+2\cdot f_{\mathrm{vib}}$

Ein zweiatomiges Molekül wie molekularer Wasserstoff hat – neben den elektronischen Anregungen – sechs Freiheitsgrade: drei der Translation, zwei der Rotation, und einen Schwingungsfreiheitsgrad. Rotation und Schwingung sind quantisiert und bei geringer Gesamtenergie eines Moleküls können energetisch höher liegende Rotations- und Schwingungsfreiheitsgrade nicht angeregt werden; man sagt, sie seien „eingefroren“. Rotation wird bereits ab mittleren, Schwingung erst bei höheren Temperaturen angeregt. So verhalten sich die meisten zweiatomigen Gase wie z. B. Wasserstoff, Sauerstoff oder Stickstoff unter Normalbedingungen effektiv so, als hätten die Einzelmoleküle nur fünf Freiheitsgrade, was sich am Adiabatenexponenten ablesen lässt. Bei hohen Temperaturen sind dem System alle Freiheitsgrade zugänglich.

Freiheitsgrade der Zustandsgrößen

Die thermodynamischen Freiheitsgrade der Zustandsgrößen auf makroskopischer Ebene ergeben sich für beliebige Systeme im thermodynamischen Gleichgewicht über die Gibbssche Phasenregel.

Weblinks

• chemgapedia.de – Freiheitsgrade von Molekülen (mit Animationen)

Einzelnachweise