Schottky-Effekt

Der Schottky-Effekt bewirkt die Verringerung der Austrittsarbeit für Elektronen an einer Metalloberfläche durch eine hohe elektrische Feldstärke im Außenraum. Dieser Effekt tritt bei Glühkathoden (Metall-Vakuum Grenzfläche) und auch Schottky-Kontakten (Metall-Halbleiter-Kontakten) wie den Schottky-Dioden auf. Der Effekt wurde nach dem deutschen Physiker Walter Schottky benannt.

Erklärung

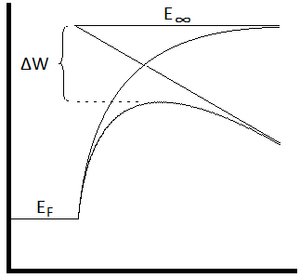
Verringerte Austrittsarbeit durch den Schottky-Effekt. Die obere Kurve ist das Bildkraftpotential, das sich dem Vakuumniveau asymptotisch nähert. Der Abstand des Vakuumpotentials vom Fermi-Niveau E_F im Metall ist die ursprüngliche Austrittsarbeit. Die untere Kurve ist die Summe aus dem Bildkraftpotential und dem linear abfallenden Potential eines äußeren homogenen Feldes. Die Höhe des sich ergebenden Maximums über E_F ist die verminderte Austrittsarbeit.

Der Einfachheit halber wird zuerst eine Metalloberfläche im Vakuum betrachtet. Ein Elektron in Entfernung $ x $ induziert eine positive Ladung an der Metalloberfläche. Die anziehende Kraft zwischen der induzierten Ladung und dem Elektron entspricht genau der Kraft zwischen dem Elektron und einer gleich großen positiven Spiegelladung bei $ -x $ und wird Spiegel- oder Bildkraft genannt.

$ F(x)={\frac {-e^{2}}{4\pi \varepsilon _{0}(2x)^{2}}} $

Mit $ \varepsilon _{0} $ der Dielektrizitätskonstanten. Die Potenzielle Energie des Elektrons ergibt sich aus der Arbeit $ W $ die verrichtet werden muss, um das Elektron von $ \infty $ bis nach $ x $ zu bringen:

$ E_{\text{Bild}}(x)=W(x)=-\int _{\infty }^{x}{F(x')dx'}=-{\frac {e^{2}}{16\pi \varepsilon _{0}}}\cdot {\frac {1}{x}} $

(Die Arbeit ist negativ, denn die anziehende Kraft zwischen Elektron und Spiegelladung wirkt in Richtung der Integration.)

Ein linearer Potentialverlauf aus einem homogenen Feld $ E $ im Außenraum überlagert sich dem Bildkraftpotential zu

$ E_{\mathrm {pot} }(x)=-{\frac {e^{2}}{16\pi \varepsilon _{0}}}\cdot {\frac {1}{x}}-eEx $.

Falls das externe Feld sehr stark ist, führt es schon innerhalb der kurzen Reichweite der Spiegelkraft zu einer Absenkung des Potentials. Mit steigender Feldstärke rückt das Maximum des Potentialverlaufs dichter an die Oberfläche heran,

$ x_{\mathrm {max} }={\sqrt {\frac {e}{16\pi \varepsilon _{0}E}}}\,, $

und sinkt dabei ab um

$ \Delta W={\sqrt {\frac {e^{3}E}{4\pi \varepsilon _{0}}}}\,. $

Für ein elektrisches Feld der Stärke $ E=10^{7}\,\mathrm {V} /\mathrm {m} $ ergibt das $ x_{\mathrm {max} }\approx 6\,\mathrm {nm} $ und $ \Delta W\approx 0{,}12\,\mathrm {eV} $, was die Stromstärke der Schottky-Emission (siehe Edison-Richardson-Effekt) bei 1000 Kelvin etwa vervierfachen würde. Allgemein erhöht der Schottky-Effekt die Stromstärke der Glühemission um den Faktor $ \mathrm {e} ^{\Delta W/(k_{\mathrm {B} }T)} $.

Für höhere Feldstärken als $ E=10^{8}\,\mathrm {V} /\mathrm {m} $ muss der Tunneleffekt berücksichtigt werden, denn die Breite der Barriere ist dann nicht mehr groß gegen die Wellenlänge der Elektronen. Bei $ E=10^{9}\,\mathrm {V} /\mathrm {m} $ ist der Tunnelstrom selbst bei kalter Elektrode beträchtlich, siehe Feldemission.

Das obige Prinzip gilt auch an Metall-Halbleiter-Grenzschichten. Das „äußere“ Feld existiert in diesem Fall selbst mit kurzgeschlossenen Anschlüssen, nämlich durch die Raumladungszone im Halbleitermaterial (dessen Dielektrizitätskonstante in den Formeln zu berücksichtigen ist).