Statischer Auftrieb: Unterschied zwischen den Versionen

Ein Gegenstand wiegt weniger, wenn er in eine Flüssigkeit eintaucht – je nach Masse der verdrängten Flüssigkeit wird entsprechend dem archimedischen Prinzip die Gewichtskraft verringert.

Der statische Auftrieb (in Flüssigkeiten auch hydrostatischer Auftrieb,^[1] in Gasen aerostatischer Auftrieb) ist das Phänomen, dass ein Körper, der in ein ruhendes Fluid (eine Flüssigkeit oder ein Gas) eintaucht, scheinbar an Gewicht verliert.^[2] Es wirkt, als wäre der Körper leichter geworden, er kann sogar „nach oben gezogen werden“. Anders gesagt: Seine Gewichtskraft wird teilweise, vollständig oder überschießend durch die statische Auftriebskraft (auch hydrostatische Auftriebskraft^[3]) kompensiert.

Der (hydro)statische Auftrieb wird oft mit der (hydro)statischen Auftriebskraft gleichgesetzt,^[4] obwohl man mit Auftrieb eigentlich nur den Effekt bezeichnet, der durch die Kraft entsteht.

Ist die Gewichtskraft des Körpers größer als die aktuell wirkende Auftriebskraft, so sinkt der Körper im Fluid ab. Im Jargon der Marine wird dies auch negativer Auftrieb oder Untertrieb genannt, beispielsweise bei Untertriebszellen von U-Booten. Ist die Gewichtskraft kleiner, so steigt der Körper im Fluid auf. Eine durch Auftrieb angetriebene Bewegung endet, wenn Auftriebskraft und Gewichtskraft ein neues Gleichgewicht gefunden haben. Ein Heißluftballon steigt beispielsweise so weit auf, bis er eine Luftschicht geringerer Dichte erreicht hat, die einen geringeren Auftrieb verursacht und die gleiche Dichte wie der Ballon hat. Beim Kräftegleichgewicht schwebt der Ballon dann ohne Höhenänderung. Das Gleichgewicht kann sich bei einem an die Wasseroberfläche auftauchenden U-Boot dadurch einstellen, dass es das Wasser teilweise verlässt und sich der Auftrieb dadurch reduziert. Das U-Boot schwimmt an der Oberfläche.

Die Stärke des statischen Auftriebs ergibt sich aus dem archimedischen Prinzip, hängt also ab von der Gewichtskraft, die auf das nun verdrängte Fluid gewirkt hat. Oft wird die Dichte des Körpers mit der des Fluids verglichen, um eine Aussage über Absinken, Schweben oder Aufsteigen des Körpers zu treffen. Veraltet ist der Bezug zur Wichte des Fluids.

Werden Objekte von Fluid umströmt, kann auch der dynamische Auftrieb wirken (der, wenn er als Anpressdruck nach unten gerichtet ist, auch als Abtrieb bezeichnet wird), dieser dynamische Auftrieb ist das physikalische Wirkprinzip für das Fliegen von Vögeln, Flugzeugen und Hubschraubern.

Physikalischer Hintergrund

Die Kraft des Wassers auf die Unterseite (b) ist größer als die Kraft des Wassers auf die Oberseite (a). Die seitlichen Kräfte (c) und (d) heben sich gegenseitig auf. Sie sind für den Auftrieb ohne Bedeutung.

Die Auftriebskraft eines in einem Fluid eingetauchten Körpers kommt daher, dass der Druck eines Fluides im Schwerefeld, der sogenannte hydrostatische Druck, mit der Tiefe zunimmt,^[5] also bei jedem ausgedehnten Körper „unten“ und „oben“ verschieden groß ist. Taucht beispielsweise ein quaderförmiger Körper mit seiner Grundfläche in ein Fluid ein, so ist der hydrostatische Druck an der Grundfläche (im Bild als b gekennzeichnet) größer als an der Oberseite (a).^[5] Bei unregelmäßiger geformten Körpern ist die statische Auftriebskraft die resultierende Kraft aus den (vertikalen) Kraftanteilen der hydrostatischen Drücke, die an allen Oberflächenteilen angreifen.^[5]

Anhand des untergetauchten Quaders kann man herleiten: Auf einen Körper, der in ein Fluid mit der Dichte $ \rho $ getaucht ist, wirkt eine Auftriebskraft $ F_{\mathrm {A} } $ mit dem Betrag:

$ F_{\mathrm {A} }=g\rho V $

Dabei ist $ V $ das vom Körper verdrängte Volumen des Fluids, $ g $ die Erdfallbeschleunigung.

Das Produkt aus Dichte und Volumen $ \rho V $ ist die Masse $ m $ des vom Körper verdrängten Fluids. Und $ g\rho V $ ist ihre Gewichtskraft. Die statische Auftriebskraft entspricht somit der Gewichtskraft des Fluids, welches sich an Stelle des eingetauchten Körpers befinden würde.

$ F_{\mathrm {A} {\text{, Körper}}}=F_{\mathrm {G} {\text{, Fluid}}} $

Dieser Zusammenhang ist als archimedisches Prinzip bekannt.

Wird die statische Auftriebskraft $ {\vec {F}}_{\mathrm {A} } $ mit der Gewichtskraft $ {\vec {F}}_{\mathrm {G} } $ des betrachteten Körpers verglichen, dann ist für diesen Vergleich das Verhältnis der Dichten von Körper und Fluid entscheidend. Man fasst das dann auch so zusammen, dass ein Körper in einem Fluid dann schwebt, wenn seine mittlere Dichte genau gleich der des umgebenden Fluids ist, dass er bei einer geringeren Dichte aufsteigt bzw. bei einer größeren Dichte absinkt.

Das hydrostatische Paradoxon sagt aus, dass der Druck nur von der Tiefe und nicht von der Form eines Fluids abhängt. Daher ist die Auftriebskraft unabhängig von der Menge des Fluids, in dem der Körper eingetaucht ist. Das Prinzip gilt demnach auch, wenn etwa die noch vorhandene Flüssigkeit ein geringeres Volumen besitzt als der eingetauchte Teil des Schwimmkörpers.

Die Auftriebskraft ist kleiner als die Gewichtskraft: Sinken

• 

  Dasymeter bei normalem Luftdruck: Beide Körper scheinen die gleiche Masse zu haben

• 

  Dasymeter im Vakuum: Wegen des fehlenden Auftriebs sind die beiden Körper ungleicher Dichte nicht mehr im Gleichgewicht

• 

  Zeppelin beim Landemanöver (1936), zum austarieren wird Wasserballast (vorne) abgelassen

Nicht nur beim Eintauchen in ein Schwimmbecken wirkt auf jeden Körper eine Auftriebskraft, auch in Luft ist das so. Dieser Effekt ist unter normalen Umständen viel kleiner (~Faktor 1000) als in einer Flüssigkeit, zur präzisen Wägung muss allerdings berücksichtigt werden, dass man bei Massenbestimmung in Luft nur den Wägewert als Näherungswert erhält. Auch bei kleinen Körpern wie Öltröpfchen in Luft muss für genaue Messungen der Kräftebilanz der Auftrieb berücksichtigt werden, siehe dazu Millikan-Versuch.

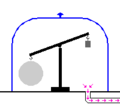
Der Legende nach sollte Archimedes von Syrakus den Goldgehalt einer Krone prüfen und tauchte dazu einmal die Krone und dann einen Goldbarren gleichen Gewichts in einen vollen Wasserbehälter und maß die Menge des überlaufenden Wassers. Galileo Galilei vermutete, Archimedes habe stattdessen ähnlich wie oben abgebildet eine Balkenwaage genutzt, um Dichteunterschiede durch unterschiedlichen Auftrieb im Wasser zu messen.

Die Auftriebskraft ist größer als die Gewichtskraft: Aufsteigen

• 

  Dampfhaltige Rauchgase steigen auf, weil sie Auftrieb in der kalten (und dichteren) Umgebungsluft haben

• 

  Feuer von feuchtem Laub im offenen Abbrand (ohne Kamineffekt) ergibt kühlere durch Ruß schwerere Rauchgase, die wenig Auftrieb zeigen

• 

  Beim Rheinhochwasser 1993 schwamm der im Rohbau befindliche Schürmann-Bau (im Vordergrund) im gestiegenen Grundwasser auf, das Gebäude hob sich stellenweise bis zu 70 Zentimeter.^[6]

• Heißluft- und Gasballone, sowie Luftschiffe steigen auf, wenn ihre mittlere Dichte geringer als die der umgebenden Luft ist. Dies wird entweder durch ein Traggas mit geringerer Dichte als Luft oder durch erwärmte Luft erreicht. Warme Luft besitzt ebenfalls eine geringere Dichte als die umgebende Luft. Kühlt bei einem Heißluftballon die innere Luftfüllung ab, so sinkt der Ballon bis die Luft erneut erwärmt wird. Eine durch Auftrieb verursachte vertikale Beschleunigung endet, wenn Auftriebskraft und Gewichtskraft im Gleichgewicht sind. Beispielsweise steigt ein Heißluftballon so weit auf, bis er eine Luftschicht erreicht hat, welche die gleiche mittlere Dichte wie der gesamte Ballon (inkl. Beladung) hat. Im entstandenen Kräftegleichgewicht schwebt der Ballon dann ohne Höhenänderung. Das Gleichgewicht stellt sich bei einem an die Wasseroberfläche auftauchenden U-Boot dadurch ein, dass es sich so weit aus dem Wasser hebt, dass die aus der Wasserverdrängung resultierende Auftriebskraft gleich der Gewichtskraft ist. Das U-Boot schwimmt dann an der Oberfläche.
• Bei der natürlichen Konvektion sorgen Dichteunterschiede für eine Schwerkraftzirkulation, die bei der (veralteten) Schwerkraftheizung genutzt wurde.
• Gerätetaucher tarieren mit Hilfe einer Tarierweste, die über die Pressluftflasche gefüllt werden kann. Ein Füllen der Tarierweste führt zu höherem Auftrieb und der Taucher steigt auf. Da mit abnehmender Tauchtiefe der Wasserdruck weiter sinkt, dehnt sich (wegen der Kompressibilität der Luft) die Tarierweste weiter aus, und der Taucher steigt noch schneller auf. Um nicht an die Wasseroberfläche getrieben zu werden, muss wieder Luft aus der Tarierweste abgelassen werden. Auch die Atmung der Pressluft führt zu einer Volumenänderung des Oberkörpers. Dieser Effekt kann ebenfalls in kleinerem Rahmen zur Tarierung verwendet werden.
• Vulkanismus, Geysire oder Schlammtöpfe basieren auf Auftriebseffekten ebenso wie das Aufsteigen von Dampfblasen vom Gefäßgrund einer beim Kochen von unten erhitzten Flüssigkeit.
• Unterkellerte Bauwerke sind bei hohem Grundwasserstand vom Auftrieb bedroht. Ein Haus mit einem wasserdichten Keller aus Stahlbeton kann bei steigendem Wasser aufschwimmen. Deshalb werden solche Keller bei Überschwemmungen zuweilen absichtlich geflutet. Ebenso können leere Schwimmbecken im dann erhöhten Grundwasser aufschwimmen. Bei Hochwasser kann der Heizöltank im gefluteten Tankraum aufschwimmen, kippen, Leitungen können abreißen und lecken.
• Spätzle oder Knödel werden im Kochtopfwasser nach oben steigen, wenn eingeschlossene nunmehr erwärmte Luft eine Volumenvergrößerung und damit eine Dichteverminderung bewirkt. Daran erkennt man die vollständige Durchwärmung und dass sie gar sind.^[7]
• CO₂-Blasen im Sekt steigen wegen des Auftriebs auf.^[8]

Die Auftriebskraft ist gleich der Gewichtskraft

Schweben

• 

  Solarballon

• Wenn ein Mensch (in einem Floatingtank) in Wasser schwebt oder an der Oberfläche als „Toter Mann“ treibt, dann erfährt er etwa die gleiche Erfahrung wie bei Schwerelosigkeit. In diesem Zustand der Schwebe wird das Gewicht scheinbar Null. Aus diesem Grund bereiten sich Raumfahrer in Wasserbecken auf die Schwerelosigkeit vor und trainieren dort Arbeiten, die sie beispielsweise außerhalb der Raumstation oder Raumfähre durchzuführen haben.^[9]
• U-Boote: Beim statischen Tauchen werden Ballasttanks gezielt geflutet. Ein U-Boot kann dadurch in einer bestimmten Wassertiefe gehalten werden.

Schwimmen an der Oberfläche

Wegen des höheren Salzgehalts im Toten Meer ist die Dichte des Wassers höher als etwa in der Nordsee, dies führt aufgrund gleicher Auftriebskraft zu einer geringeren Einsinktiefe.

Wirkt auf einen ruhenden teilweise eingetaucht schwimmenden Körper (z. B. ein Schiff) neben seiner Gewichtskraft $ {\vec {F}}_{\mathrm {G} } $ ausschließlich der statische Auftrieb $ {\vec {F}}_{\mathrm {A} } $, dann gilt für die Auftriebskraft im statischen Gleichgewicht

$ {\vec {F}}_{\mathrm {A} }=-{\vec {F}}_{\mathrm {G} } $^{[10][11][12][13]}

unabhängig von der Dichte des Wassers, welche aber Einfluss auf die Eindringtiefe des Körpers hat (im Gleichgewicht $ {F_{\mathrm {A} }}/{({\bar {\rho }}V)}={\bar {g}} $ )

Das so genannte Schwimmgleichgewicht^[14] besagt dass:

$ {\frac {\text{Eintauchendes V}}{\text{Gesamtvolumen}}}={\frac {\text{Dichte d. schwimmenden Körpers}}{\text{Dichte der Flüssigkeit}}} $ ^[14]

Nutzung: Tiefgang von Schiffen

Schwimmende Schiffe befinden sich in einem stabilen Gleichgewicht: Wenn sie in hohem Wellengang tiefer eintauchen, dann vergrößern sich das verdrängte Wasservolumen und somit der Auftrieb und sie werden wieder emporgehoben. Werden sie zu weit emporgehoben, dann verringern sich das verdrängte Wasservolumen und der Auftrieb, und die Schwerkraft lässt sie wieder eintauchen.

Krängt ein Schiff nach einer Seite, z. B. bei Drehkreisfahrt oder Seitenwind, so erhöht sich der Tiefgang an dieser Seite, während er sich an der anderen Seite verringert. Entsprechend den veränderten Druckverhältnissen verschiebt sich der Auftriebsmittelpunkt und es entsteht ein Moment, das der Krängung entgegenwirkt und das Schiff wieder in die Ausgangslage bringt, sobald die äußere Einwirkung nachlässt.

Wird ein Schiff beladen vergrößert sich seine Gewichtskraft, deshalb sinkt es tiefer ins Wasser ein und verdrängt mehr Wasser als im unbeladenen Zustand. Wegen der größeren Einsinktiefe wirkt dann mehr Auftriebskraft, diese steht immer mit der (nun größeren) Gewichtskraft im Gleichgewicht.

Fährt dieses Schiff von der Nordsee in die Elbe und wechselt somit vom Salzwasser ins Süßwasser (das eine geringere Dichte hat als Salzwasser), würde im Süßwasser bei unveränderter Eintauchtiefe die Auftriebskraft abnehmen. Daher sinkt das Schiff tiefer ein bis die Auftriebskraft des größeren Einsinkvolumens wiederum mit der Gewichtskraft des Schiffes im Gleichgewicht steht.

Freibordmarke (links) und Lademarke (rechts) an einem Schiff: TF = Freibord Süßwasser Tropen
F = Freibord in Süßwasser
T = Freibord in tropischem Seewasser (Salzwasser des Meers)
S = Sommerlademarke in Seewasser
W = Freibord in Seewasser im Winter
WNA = Freibord in Seewasser im Winter im Nordatlantik

Lademarken an Schiffen kennzeichnen die (erlaubten) Eintauchtiefen in Wasser unterschiedlicher Dichte. Die obersten zwei waagrechten Stufenoberkanten (Richtung kreisförmiger) Freibordmarke für Süßwasser der Binnengewässer, vier untereinander tiefer liegende für das dichtere Salzwasser der Meere mit unterschiedlicher Temperatur.

Steigen Methan­blasen von submarinen Methanhydrat-Lagerstätten auf, so kann das für die Schifffahrt eine Gefahr darstellen. Schottische Wissenschaftler führen darauf das Sinken eines im Hexenloch in der Nordsee entdeckten Fischkutters zurück. Die aufsteigenden Gasblasen können demnach die Dichte des Meerwassers so sehr verringern, dass Schiffe schlagartig ihre Schwimmfähigkeit verlieren.^[15][16]

Anwendung: Dichtemessung, Temperaturmessung

Auf ein Aräometer (auch Dichtespindel genannt) das in eine Flüssigkeit mit der Dichte $ \rho $ getaucht ist, wirkt ebenfalls eine Auftriebskraft $ F_{\mathrm {A} } $ mit dem Betrag:

$ F_{\mathrm {A} }=g\rho V $

Aus der Eindringtiefe kann daher auf die Dichte der Flüssigkeit und damit gegebenenfalls auf den Gehalt gelöster Stoffe geschlossen werden, was auf einer an den Zweck des Aräometers angepassten Skala abgelesen werden kann. Typisches Beispiel hierfür ist das Skalenaräometer.

Bei einem Flüssigkeits­thermometer nach Galileo Galilei ordnen sich die Auftriebskörper entsprechend der temperatur­abhängigen Dichte des Fluids in unterschied­lichen Höhen in der jeweiligen Gleich­gewichts­lage an

Ein Galileo-Thermometer zeigt anhand des Auftriebs verschiedener Körper in einer Flüssigkeit die Temperatur der Flüssigkeit an. Die dazu verwendeten Glaskugeln, deren Durchmesser größer ist als der halbe Innendurchmesser des Zylinders^[17] (wodurch sie in der Schichtung bleiben und sich gegenseitig nicht "überholen"), wurden mithilfe von Flüssigkeiten so austariert, dass deren mittlere Dichte von der obersten Kugel zur untersten Kugel zunimmt. Da die Dichte der Flüssigkeit temperaturabhängig ist, ändert sich der Auftrieb entsprechend der Temperatur. Bei einer bestimmten Temperatur steigen alle Kugeln auf, deren mittlere Dichten kleiner sind als die mittlere Dichte der sie umgebenden Flüssigkeit ist. Alle Kugeln sinken ab, deren mittlere Dichten größer sind als die mittlere Dichte der sie umgebenden Flüssigkeit. Die aktuelle Temperatur kann an der angehängten Plakette der oben zuunterst schwimmenden Kugel abgelesen werden.^[17] Erwärmt sich dann die Flüssigkeit, nimmt also ihre Dichte ab, so sinkt eine weitere Kugel ab und die neue Temperatur kann wieder an der angehängten Plakette der oben zuunterst schwimmenden Kugel abgelesen werden.

Der Effekt des sich mit der Temperatur ändernden Auftriebs tritt auch bei Tauchgängen von U-Booten auf, wenn mit zunehmender Wassertiefe die Temperatur des Meerwassers abnimmt oder das U-Boot beim statischen Tauchen zwischen einer warmen und einer kalten Meeresströmung wechselt.

Siehe dazu auch die Abbildung der Schiffs-Lademarken oben, die den unterschiedlichen Auftrieb von Schiffen im Sommer und im Winter und im kalten Wasser des Nordatlantiks und in wärmeren tropischen Gewässern berücksichtigen.

Anwendung: Physikalisches Spielzeug

• Cartesischer Taucher
• Lavalampe

Siehe auch

• Fluidstatik
• Aerostatik
• Isostasie

Weblinks

Wiktionary: Auftrieb – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Statischer Auftrieb – Sammlung von Bildern, Videos und Audiodateien

• Herleitung der Auftriebskraft aus dem Schweredruck auf Schülerniveau (LEIFI)

Einzelnachweise