Apsidendrehung: Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Wikipedia:Vorlagenfehler/Vorlage:Literatur/Interner Fehler
- Wikipedia:Vorlagenfehler/Vorlage:Cite journal/Parameter language fehlt
- Himmelsmechanik
imported>Yukterez (→Relativistische Periheldrehung: Datei: statt Datei:File:) |
imported>Wassermaus |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:Apsidendrehung.png|mini|Die Periheldrehung der Bahn eines Planeten. Die [[Exzentrizität (Astronomie)|Exzentrizität]] der Bahn und der Betrag der Drehung sind schematisch übertrieben.]] | [[Datei:Apsidendrehung.png|mini|Die Periheldrehung der Bahn eines Planeten. Die [[Exzentrizität (Astronomie)|Exzentrizität]] der Bahn und der Betrag der Drehung sind schematisch übertrieben.]] | ||
[[Datei:Drehung der Apsidenlinie.svg|mini|Apsidendrehung und Drehung der Apsidenlinie jeweils in der [[Periapsis]]. Man sieht somit die | [[Datei:Drehung der Apsidenlinie.svg|mini|Apsidendrehung und Drehung der Apsidenlinie jeweils in der [[Periapsis]]. Man sieht somit die ''Periapsisdrehung''.]] | ||
Die '''Apsidendrehung''' einer elliptischen [[Umlaufbahn]] ist eine fortschreitende Drehung der ganzen Bahn in der [[Bahnebene]]. Dabei dreht sich die [[Apsis (Astronomie)|Apsidenlinie]] kontinuierlich, während Form und Ebene der Bahn im Raum gleich bleiben. Je nach Zentralkörper werden auch folgende Bezeichnungen verwendet: | Die '''Apsidendrehung''' einer elliptischen [[Umlaufbahn]] ist eine fortschreitende Drehung der ganzen Bahn in der [[Bahnebene]]. Dabei dreht sich die [[Apsis (Astronomie)|Apsidenlinie]] kontinuierlich, während Form und Ebene der Bahn im Raum gleich bleiben. Je nach Zentralkörper werden auch folgende Bezeichnungen verwendet: | ||
| Zeile 8: | Zeile 8: | ||
== Ursachen == | == Ursachen == | ||
Eine Apsidendrehung entsteht, wenn ein [[Himmelskörper]] auf seiner [[Ellipse|elliptischen]] Umlaufbahn um einen Zentralkörper bestimmten äußeren Störungen unterliegt. Wäre der Himmelskörper einer Anziehungskraft ausgesetzt, welche streng umgekehrt quadratisch mit der Entfernung vom Zentralkörper abnimmt, so würde er sich exakt auf einer [[Keplerbahn|Keplerellipse]] bewegen, deren Form, Lage und Orientierung im Raum unverändert blieben. Abweichungen vom streng umgekehrt-quadratischen Kraftgesetz führen jedoch zu verschiedenen Arten von [[Bahnstörung]]en, welche Form, Lage und Orientierung der Bahn verändern können. Eine dieser Bahnstörungen ist die Apsidendrehung. | Eine Apsidendrehung entsteht, wenn ein [[Himmelskörper]] auf seiner [[Ellipse|elliptischen]] Umlaufbahn um einen Zentralkörper bestimmten äußeren Störungen unterliegt. Wäre der Himmelskörper einer Anziehungskraft ausgesetzt, welche streng umgekehrt quadratisch mit der Entfernung vom Zentralkörper abnimmt, so würde er sich exakt auf einer [[Keplerbahn|Keplerellipse]] bewegen, deren Form, Lage und Orientierung im Raum unverändert blieben. Nach dem Satz von Bertrand sind die einzigen zentralsymmetrischen Potentiale mit geschlossenen Bahnen das 1/r-Potential und das Potential des harmonischen Oszillators mit radialem Funktionsverlauf proportional r<sup>2</sup>. Abweichungen vom streng umgekehrt-quadratischen Kraftgesetz führen jedoch zu verschiedenen Arten von [[Bahnstörung]]en, welche Form, Lage und Orientierung der Bahn verändern können. Eine dieser Bahnstörungen ist die Apsidendrehung. | ||
* Eine mögliche Ursache für Abweichungen vom | * Eine mögliche Ursache für Abweichungen vom 1/r<sup>2</sup>-Zentralkraftgesetz ist die Gegenwart anderer Körper, welche zusätzliche [[Gravitation]]skräfte auf den betrachteten Himmelskörper ausüben. Im Falle der Planetenbahnen ist der Einfluss der jeweils anderen Planeten die Hauptursache für die Periheldrehungen. | ||
* Eine andere Ursache kann in Abweichungen des Zentralkörpers von der [[Kugel]]form liegen. Während ein exakt kugelsymmetrisch aufgebauter ausgedehnter Körper dasselbe streng invers-quadratische Gravitationsfeld erzeugen würde wie ein punktförmiger Körper derselben Masse, führen unregelmäßige Masseverteilungen oder der Äquatorwulst [[Abplattung|abgeplatteter]] Zentralkörper | * Eine andere Ursache kann in Abweichungen des Zentralkörpers von der [[Kugel]]form liegen. Während ein exakt kugelsymmetrisch aufgebauter ausgedehnter Körper dasselbe streng invers-quadratische Gravitationsfeld erzeugen würde wie ein punktförmiger Körper derselben Masse, führen unregelmäßige Masseverteilungen oder der Äquatorwulst [[Abplattung|abgeplatteter]] Zentralkörper zu Abweichungen vom invers-quadratischen Kraftgesetz und damit zu Bahnstörungen. Der Äquatorwulst der Erde verursacht (neben anderen Bahnstörungen) Perigäumsdrehungen bei [[Satellit (Raumfahrt)|künstlichen Erdsatelliten]]. Die Abplattung der Sonne verursacht Periheldrehungen der Planetenbahnen, welche wegen der Geringfügigkeit der Abplattung und des großen Abstandes der Planeten jedoch wesentlich kleiner sind als die von den Planeten untereinander verursachten Drehungen. | ||
* | * Die Krümmung der Raumzeit, ein Effekt der [[Allgemeine Relativitätstheorie|Allgemeinen Relativitätstheorie]], bewirkt eine Abweichung von den Newtonschen Bewegungsgleichungen (siehe [[Effektives Potential#Allgemeine Relativitätstheorie]]). Dadurch entsteht ein Beitrag zur Periheldrehung, der Schwarzschild-Präzession genannt wird. | ||
* Es gibt Hypothesen, dass das idealisierte Kraftgesetz selbst vom invers-quadratischen Verhalten abweicht (z. B. die [[Modifizierte Newtonsche Dynamik]]). Dies würde ebenfalls zur Apsidendrehung beitragen. | |||
Aus all diesen Ursachen resultiert – in einem bezüglich des [[Fixstern]]hintergrunds ruhenden [[Astronomische Koordinatensysteme|Koordinatensystem]] – eine [[Rosette (Architektur)|rosettenartige]] Bewegung des Körpers: Die ''[[anomalistische Periode]]'' entspricht nicht genau der ''[[Siderische Periode|siderischen]]''. Himmelsmechanisch wird das durch einen langperiodischen [[Term]] des [[Bahnelement]]s ''[[Argument des Perizentrum]]s'' beschrieben. | Aus all diesen Ursachen resultiert – in einem bezüglich des [[Fixstern]]hintergrunds ruhenden [[Astronomische Koordinatensysteme|Koordinatensystem]] – eine [[Rosette (Architektur)|rosettenartige]] Bewegung des Körpers: Die ''[[anomalistische Periode]]'' entspricht nicht genau der ''[[Siderische Periode|siderischen]]''. Himmelsmechanisch wird das durch einen langperiodischen [[Term]] des [[Bahnelement]]s ''[[Argument des Perizentrum]]s'' beschrieben. | ||
Wird die Bahn nicht in einem bezüglich des Fixsternhintergrunds ruhenden Bezugssystem beschrieben, sondern in einem rotierenden Bezugssystem, so kommt zu den oben beschriebenen physikalisch verursachten Drehungen eine zusätzliche scheinbare Drehung hinzu, welche lediglich die Drehung des Bezugssystems widerspiegelt. Im Falle der Planetenbahnen des Sonnensystems betragen die Periheldrehungen – von einem fest gewählten [[Äquinoktium|Frühlingspunkt]] aus gezählt – nur Bruchteile eines Grades pro Jahrhundert. Werden die Bahnen hingegen bezüglich des beweglichen [[Äquinoktium|Äquinoktiums des Datums]] beschrieben, so sind ihre Geschwindigkeiten in diesem rotierenden Bezugssystem um die [[Präzession]]sgeschwindigkeit des Frühlingspunkts, nämlich 1,396° pro Jahrhundert, höher und liegen zwischen | Wird die Bahn nicht in einem bezüglich des Fixsternhintergrunds ruhenden Bezugssystem beschrieben, sondern in einem rotierenden Bezugssystem, so kommt zu den oben beschriebenen physikalisch verursachten Drehungen eine zusätzliche scheinbare Drehung hinzu, welche lediglich die Drehung des Bezugssystems widerspiegelt. Im Falle der Planetenbahnen des Sonnensystems betragen die Periheldrehungen – von einem fest gewählten [[Äquinoktium|Frühlingspunkt]] aus gezählt – nur Bruchteile eines Grades pro Jahrhundert. Werden die Bahnen hingegen bezüglich des beweglichen [[Äquinoktium|Äquinoktiums des Datums]] beschrieben, so sind ihre Geschwindigkeiten in diesem rotierenden Bezugssystem um die [[Präzession]]sgeschwindigkeit des Frühlingspunkts, nämlich 1,396° pro Jahrhundert, höher und liegen zwischen 1° und 2° pro Jahrhundert. | ||
== Episoden aus der Forschungsgeschichte == | == Episoden aus der Forschungsgeschichte == | ||
| Zeile 22: | Zeile 23: | ||
Bereits den [[Geschichte der Astronomie|antiken Astronomen]] war durch Beobachtung bekannt, dass Sonne, Mond und Planeten ihre Bahnen nicht mit konstanten Geschwindigkeiten durchlaufen. Griechische Astronomen berücksichtigten dies in ihren Planetentheorien, indem sie den Mittelpunkt der jeweiligen als kreisförmig vorausgesetzten Planetenbahn nicht mit dem Mittelpunkt der im Zentrum des Universums angenommenen Erde zusammenfallen ließen, sondern in geeigneter Richtung um einen bestimmten Betrag (die so genannte ''Exzentrizität'', nicht zu verwechseln mit der [[Exzentrizität (Mathematik)|Exzentrizität]] einer Ellipsenbahn) versetzten. Auf der dem Beobachter näher liegenden Bahnhälfte bewegte sich der gleichmäßig laufende Planet nun scheinbar schneller als auf der gegenüberliegenden Hälfte. Wie sich zeigen lässt, kann der reale, dem [[Keplersche Gesetze|2. Keplerschen Gesetz]] folgende Geschwindigkeitsverlauf eines Planeten in sehr guter Näherung mittels einer geeignet verschobenen Kreisbahn (einem so genannten ''[[Exzenter (Astronomie)|Exzenter]]'') rechnerisch nachvollzogen werden. [[Hipparchos (Astronom)|Hipparchos]] beispielsweise schloss aus den ungleichen Längen der [[Jahreszeiten]] auf die Geschwindigkeitsvariation der (damals als Planet behandelten) Sonne in den einzelnen Bahnquadranten und beschrieb ihren Umlauf durch einen Kreis, welcher um 1/24 seines Radius in Richtung 65,5° verschoben war.<ref>(Ptolemäus 150) Buch 3, Kap. 4</ref> In dieser Richtung lag also auch das [[Erdnähe|Apogäum]] der Sonnenbahn, dessen [[ekliptikale Länge]] damals auch tatsächlich 66,23° betrug.<ref>(Pedersen 1974) S. 147</ref> (Damals wurde das Apogäum als Bezugspunkt benutzt, während man heute das [[Erdnähe|Perigäum]] bevorzugt.) | Bereits den [[Geschichte der Astronomie|antiken Astronomen]] war durch Beobachtung bekannt, dass Sonne, Mond und Planeten ihre Bahnen nicht mit konstanten Geschwindigkeiten durchlaufen. Griechische Astronomen berücksichtigten dies in ihren Planetentheorien, indem sie den Mittelpunkt der jeweiligen als kreisförmig vorausgesetzten Planetenbahn nicht mit dem Mittelpunkt der im Zentrum des Universums angenommenen Erde zusammenfallen ließen, sondern in geeigneter Richtung um einen bestimmten Betrag (die so genannte ''Exzentrizität'', nicht zu verwechseln mit der [[Exzentrizität (Mathematik)|Exzentrizität]] einer Ellipsenbahn) versetzten. Auf der dem Beobachter näher liegenden Bahnhälfte bewegte sich der gleichmäßig laufende Planet nun scheinbar schneller als auf der gegenüberliegenden Hälfte. Wie sich zeigen lässt, kann der reale, dem [[Keplersche Gesetze|2. Keplerschen Gesetz]] folgende Geschwindigkeitsverlauf eines Planeten in sehr guter Näherung mittels einer geeignet verschobenen Kreisbahn (einem so genannten ''[[Exzenter (Astronomie)|Exzenter]]'') rechnerisch nachvollzogen werden. [[Hipparchos (Astronom)|Hipparchos]] beispielsweise schloss aus den ungleichen Längen der [[Jahreszeiten]] auf die Geschwindigkeitsvariation der (damals als Planet behandelten) Sonne in den einzelnen Bahnquadranten und beschrieb ihren Umlauf durch einen Kreis, welcher um 1/24 seines Radius in Richtung 65,5° verschoben war.<ref>(Ptolemäus 150) Buch 3, Kap. 4</ref> In dieser Richtung lag also auch das [[Erdnähe|Apogäum]] der Sonnenbahn, dessen [[ekliptikale Länge]] damals auch tatsächlich 66,23° betrug.<ref>(Pedersen 1974) S. 147</ref> (Damals wurde das Apogäum als Bezugspunkt benutzt, während man heute das [[Erdnähe|Perigäum]] bevorzugt.) | ||
[[Ptolemäus]] wiederholte die Bahnbestimmung 300 Jahre später. Da seine Beobachtungen aber dieselben Längen für die Jahreszeiten ergaben, erhielt er auch dieselbe Sonnenbahn und hielt daher die Lage ihres Apogäums für unveränderlich bezüglich der [[Äquinoktium|Äquinoktialpunkte]]: | [[Ptolemäus]] wiederholte die Bahnbestimmung 300 Jahre später. Da seine Beobachtungen aber dieselben Längen für die Jahreszeiten ergaben, erhielt er auch dieselbe Sonnenbahn und hielt daher die Lage ihres Apogäums für unveränderlich bezüglich der [[Äquinoktium|Äquinoktialpunkte]]: | ||
{{Zitat|<!-- alte Rechtschreibung, Zitat! -->Auch wir gelangen zu dem Ergebnis, dass noch heutzutage die Zeiten der obenbezeichneten Quadranten und die angegebenen Verhältnisse nahezu dieselben sind, woraus uns ersichtlich wird, dass der Exzenter der Sonne zu den Wende- und Nachtgleichenpunkten ewig dieselbe Lage bewahrt.<!-- alte Rechtschreibung, Zitat! -->|ref=<ref>(Ptolemäus 150) Buch 3, Kap. 4; Manitius Bd. I S. 167</ref>}} | {{Zitat|<!-- alte Rechtschreibung, Zitat! -->Auch wir gelangen zu dem Ergebnis, dass noch heutzutage die Zeiten der obenbezeichneten Quadranten und die angegebenen Verhältnisse nahezu dieselben sind, woraus uns ersichtlich wird, dass der Exzenter der Sonne zu den Wende- und Nachtgleichenpunkten ewig dieselbe Lage bewahrt.<!-- alte Rechtschreibung, Zitat! -->|ref=<ref>(Ptolemäus 150) Buch 3, Kap. 4; Manitius Bd. I S. 167</ref>}} | ||
Anders verhielten sich jedoch die Apogäen der übrigen Planeten. Aus den Ergebnissen zahlreicher Beobachtungen und Auswertungen schloss er, dass deren Apogäen nicht bezüglich der Äquinoktialpunkte, sondern bezüglich der Fixsterne ruhen. Dies ist insofern bemerkenswert, als seiner Auffassung nach (und im Gegensatz zum heutigen Standpunkt) die Äquinoktialpunkte als ruhend und die Fixsterne als infolge der Präzession bewegt betrachtet wurden. Entsprechend hielt er die Apogäen für beweglich, und ihre Geschwindigkeit musste bestimmt werden. Die Beobachtungen zeigten ihm, dass sie sich alle etwa gleich schnell [[rechtläufig]] bewegten und dass ihre Geschwindigkeit im Rahmen der Beobachtungsgenauigkeit mit der Präzessionsgeschwindigkeit der Fixsterne übereinstimmte; er fand, dass | Anders verhielten sich jedoch die Apogäen der übrigen Planeten. Aus den Ergebnissen zahlreicher Beobachtungen und Auswertungen schloss er, dass deren Apogäen nicht bezüglich der Äquinoktialpunkte, sondern bezüglich der Fixsterne ruhen. Dies ist insofern bemerkenswert, als seiner Auffassung nach (und im Gegensatz zum heutigen Standpunkt) die Äquinoktialpunkte als ruhend und die Fixsterne als infolge der Präzession bewegt betrachtet wurden. Entsprechend hielt er die Apogäen für beweglich, und ihre Geschwindigkeit musste bestimmt werden. Die Beobachtungen zeigten ihm, dass sie sich alle etwa gleich schnell [[rechtläufig]] bewegten und dass ihre Geschwindigkeit im Rahmen der Beobachtungsgenauigkeit mit der Präzessionsgeschwindigkeit der Fixsterne übereinstimmte; er fand, dass | ||
{{Zitat|<!-- alte Rechtschreibung, Zitat! -->auch die Apogeen der Exzenter einen ganz geringen von den Wendepunkten aus in der Richtung der Zeichen vor sich gehenden Fortschritt bewerkstelligen, welcher wieder gleichförmig um den Mittelpunkt der Ekliptik verläuft und für alle Planeten ungefähr ebensogroß ist, wie er an der Fixsternsphäre wahrgenommen worden ist | {{Zitat|<!-- alte Rechtschreibung, Zitat! -->auch die Apogeen der Exzenter einen ganz geringen von den Wendepunkten aus in der Richtung der Zeichen vor sich gehenden Fortschritt bewerkstelligen, welcher wieder gleichförmig um den Mittelpunkt der Ekliptik verläuft und für alle Planeten ungefähr ebensogroß ist, wie er an der Fixsternsphäre wahrgenommen worden ist – d. h. in 100 Jahren vom Betrage eines Grades -, soweit es wenigstens möglich ist, aus dem vorliegenden Material einen Einblick zu gewinnen.<!-- alte Rechtschreibung, Zitat! -->|ref=<ref>(Ptolemäus 150) Buch 3, Kap. 5; Manitius Bd. II S. 121</ref>}} | ||
Im 9. Jahrhundert bemerkte [[Thabit ibn Qurrah]], dass auch das Sonnenapogäum eine rechtläufige Bewegung bezüglich der Äquinoktialpunkte ausführte.<ref>(Neugebauer 1975) S. 58</ref> Man hielt diese Bewegung zunächst aber noch wie die der Planetenapogäen für rein präzessionsbedingt. [[Al-Battani]] beispielsweise legte das Sonnenapogäum für den 1. März 880 auf 82° 15' ekliptikaler Länge und gab die Anweisung, zur Berechnung der Apogäumslänge zu anderen Zeitpunkten für jeweils 66 verstrichene Jahre 1° Präzessionsverschiebung zu addieren oder abzuziehen: | Im 9. Jahrhundert bemerkte [[Thabit ibn Qurrah]], dass auch das Sonnenapogäum eine rechtläufige Bewegung bezüglich der Äquinoktialpunkte ausführte.<ref>(Neugebauer 1975) S. 58</ref> Man hielt diese Bewegung zunächst aber noch wie die der Planetenapogäen für rein präzessionsbedingt. [[Al-Battani]] beispielsweise legte das Sonnenapogäum für den 1. März 880 auf 82° 15' ekliptikaler Länge und gab die Anweisung, zur Berechnung der Apogäumslänge zu anderen Zeitpunkten für jeweils 66 verstrichene Jahre 1° Präzessionsverschiebung zu addieren oder abzuziehen: | ||
| Zeile 33: | Zeile 34: | ||
{{Zitat|Die [Längen dieser] Apogäen bewegen sich mit der Bewegung der Fixsternsphäre, nämlich ein Grad in 66 Sonnenjahren.|ref=<ref>(al-Battani 900) S. 114 (Horum apogeorum [longitudines] motu sphaerae stellarum fixarum moventur, scilicet uno gradu in 66 annis solaribus […]", eigene Übersetzung).</ref>}} | {{Zitat|Die [Längen dieser] Apogäen bewegen sich mit der Bewegung der Fixsternsphäre, nämlich ein Grad in 66 Sonnenjahren.|ref=<ref>(al-Battani 900) S. 114 (Horum apogeorum [longitudines] motu sphaerae stellarum fixarum moventur, scilicet uno gradu in 66 annis solaribus […]", eigene Übersetzung).</ref>}} | ||
Erst [[Ibn | Erst [[Ibn asch-Schatir]] stellte im 14. Jahrhundert durch Beobachtung fest, dass das Sonnenapogäum nicht genau mit der Geschwindigkeit der Präzession wanderte (nämlich mit 1° pro 60 Persischen Jahren gegenüber 1° pro 70 Persischen Jahren), sich also bezüglich der Fixsterne eigenständig bewegte.<ref>(Saliba 1994) S. 234</ref> | ||
Im Gegensatz zu den Planetenbahnen war die Perigäumsdrehung des Mondes bereits den babylonischen Astronomen bekannt und explizit in ihren Rechenschemata berücksichtigt.<ref>(Neugebauer 1975) S. 480</ref> Hipparch und Ptolemäus übernahmen aus der babylonischen Astronomie grundlegende Zahlenwerte und arbeiteten sie zu detaillierten Mondtheorien auf Basis des [[Epizykeltheorie|Epizykelmodells]] aus.<ref>(Neugebauer 1975) S. 71</ref> | Im Gegensatz zu den Planetenbahnen war die Perigäumsdrehung des Mondes bereits den babylonischen Astronomen bekannt und explizit in ihren Rechenschemata berücksichtigt.<ref>(Neugebauer 1975) S. 480</ref> Hipparch und Ptolemäus übernahmen aus der babylonischen Astronomie grundlegende Zahlenwerte und arbeiteten sie zu detaillierten Mondtheorien auf Basis des [[Epizykeltheorie|Epizykelmodells]] aus.<ref>(Neugebauer 1975) S. 71</ref> | ||
| Zeile 46: | Zeile 47: | ||
Weitere Erklärungsversuche zogen die Gültigkeit des Newtonschen Kraftgesetzes in Zweifel. So gelang es unter Zugrundelegung von elektrodynamischen Kraftgesetzen zum Beispiel Levy (1890) und vor allem [[Paul Gerber (Physiker)|Paul Gerber]] (1898), den Überschuss vollständig abzuleiten, unter der Voraussetzung, dass die Ausbreitungsgeschwindigkeit der Gravitation gleich der [[Lichtgeschwindigkeit]] ist. Gerbers Formel für die Perihelabweichung war formal bereits identisch mit der später von Einstein aufgestellten. Jedoch waren die zugrunde gelegten Kraftgesetze falsch und die Theorien dieser Art mussten verworfen werden.<ref>Oppenheim (1920), 153ff.</ref><ref>Roseveare (1982), Kap. 6</ref> | Weitere Erklärungsversuche zogen die Gültigkeit des Newtonschen Kraftgesetzes in Zweifel. So gelang es unter Zugrundelegung von elektrodynamischen Kraftgesetzen zum Beispiel Levy (1890) und vor allem [[Paul Gerber (Physiker)|Paul Gerber]] (1898), den Überschuss vollständig abzuleiten, unter der Voraussetzung, dass die Ausbreitungsgeschwindigkeit der Gravitation gleich der [[Lichtgeschwindigkeit]] ist. Gerbers Formel für die Perihelabweichung war formal bereits identisch mit der später von Einstein aufgestellten. Jedoch waren die zugrunde gelegten Kraftgesetze falsch und die Theorien dieser Art mussten verworfen werden.<ref>Oppenheim (1920), 153ff.</ref><ref>Roseveare (1982), Kap. 6</ref> | ||
Erst die [[Allgemeine Relativitätstheorie]] von [[Albert Einstein]], die die Gravitation als Krümmung der [[Raumzeit]] beschreibt, auf deren Struktur auch die Weltkörper ihrerseits Einfluss haben, konnte den Überschuss überzeugend erklären.<ref>(Einstein 1915)</ref> Dieser Erfolg gilt als eine der Hauptstützen der Allgemeinen Relativitätstheorie und als ihre erste große Bestätigung. Der relativistisch berechnete Anteil von 42,98″<ref name="Nobili 1986">(Nobili 1986)</ref> stimmt sehr gut mit dem beobachteten Überschuss von 43,11″ überein. Die Ursache für den relativistischen Effekt liegt in der geringfügigen Abweichung des relativistisch behandelten Gravitationsfelds vom streng invers-quadratischen Verhalten.<ref>(Guthmann 2000) S. 93ff</ref> | Erst die [[Allgemeine Relativitätstheorie]] (ART) von [[Albert Einstein]], die die Gravitation als Krümmung der [[Raumzeit]] beschreibt, auf deren Struktur auch die Weltkörper ihrerseits Einfluss haben, konnte den Überschuss überzeugend erklären.<ref>(Einstein 1915)</ref> Dieser Erfolg gilt als eine der Hauptstützen der Allgemeinen Relativitätstheorie und als ihre erste große Bestätigung. Der relativistisch berechnete Anteil von 42,98″<ref name="Nobili 1986">(Nobili 1986)</ref> stimmt sehr gut mit dem beobachteten Überschuss von 43,11″ überein. Die Ursache für den relativistischen Effekt liegt in der geringfügigen Abweichung des relativistisch behandelten Gravitationsfelds vom streng invers-quadratischen Verhalten.<ref>(Guthmann 2000) S. 93ff</ref> | ||
Die Übereinstimmung zwischen Beobachtung und relativistischer Rechnung würde weniger gut ausfallen, wenn ein merklicher Teil des beobachteten Überschusses auf eine rotationsbedingte [[Abplattung]] der Sonne zurückzuführen wäre und der übrigbleibende zu erklärende Anteil daher deutlich geringer wäre als gemäß ART berechnet. Versuche, die äußerst geringe Abplattung der Sonne zu messen, lieferten über lange Zeit hinweg widersprüchliche Ergebnisse, sodass auch stets ein wenig zweifelhaft blieb, wie gut die Übereinstimmung der relativistischen Vorhersage mit der Beobachtung tatsächlich war. [[Helioseismologie|Helioseismologische]] Untersuchungen haben jedoch mittlerweile das Quadrupolmoment | Die Übereinstimmung zwischen Beobachtung und relativistischer Rechnung würde weniger gut ausfallen, wenn ein merklicher Teil des beobachteten Überschusses auf eine rotationsbedingte [[Abplattung]] der Sonne zurückzuführen wäre und der übrigbleibende zu erklärende Anteil daher deutlich geringer wäre als gemäß ART berechnet. Versuche, die äußerst geringe Abplattung der Sonne zu messen, lieferten über lange Zeit hinweg widersprüchliche Ergebnisse, sodass auch stets ein wenig zweifelhaft blieb, wie gut die Übereinstimmung der relativistischen Vorhersage mit der Beobachtung tatsächlich war. [[Helioseismologie|Helioseismologische]] Untersuchungen haben jedoch mittlerweile das [[Quadrupol#Gravitation|Quadrupolmoment]] <math>J_2</math> der Sonne zuverlässig zu (2,18 ± 0,06)·10<sup>−7</sup> bestimmt; dieses Quadrupolmoment liefert nur einen Beitrag von einigen Hundertstel Bogensekunden zur Periheldrehung und ist daher vernachlässigbar.<ref>(Will 2006) S. 38</ref> Eine andere Möglichkeit zur Bestimmung von <math>J_2</math> nutzt den Umstand, dass der relativistische und der <math>J_2</math>-bedingte Anteil an der gesamten Periheldrehung mit wachsender Entfernung von der Sonne unterschiedlich rasch abfallen und sich so durch Vergleich der Gesamtdrehungen verschiedener Planeten voneinander trennen lassen. Eine solche Untersuchung<ref>(Pitjeva 2005)</ref> lieferte mit <math>J_2</math> = (1,9 ± 0,3)·10<sup>−7</sup> ein Ergebnis, das nahe an dem der Helioseismologie liegt. | ||
Die Tabelle führt einige Beobachtungsergebnisse der letzten | Die Tabelle führt einige Beobachtungsergebnisse der Periheldrehung aus den letzten Jahrzehnten auf: | ||
{| class="wikitable" | {| class="wikitable" | ||
!Jahr | !Jahr | ||
!Autoren | !Autoren | ||
!Methode | !Methode | ||
! | !Drehung pro Jahrhundert | ||
!Quelle | !Quelle | ||
|- | |- | ||
| Zeile 61: | Zeile 62: | ||
|Morrison, Ward | |Morrison, Ward | ||
|Merkurdurchgänge | |Merkurdurchgänge | ||
|41,9″ ± 0,5″ | |41,9″{{0}} ± 0,5″ | ||
|<ref>(Morrison Ward 1975)</ref> | |<ref>(Morrison Ward 1975)</ref> | ||
|- | |- | ||
| Zeile 131: | Zeile 132: | ||
|} | |} | ||
Die Zahlenwerte beider Spalten unterscheiden sich um 1,396° pro Jahrhundert, die Rate der [[Präzession]] in ekliptikaler Länge. So ändert sich zum Beispiel der Winkel zwischen dem Perihel der Erde und dem Frühlingspunkt um 1,720°/Jahrhundert, so dass beide nach circa 21.000 Jahren wieder dieselbe Stellung zueinander einnehmen, was unter anderem Auswirkungen auf das Klima haben könnte (siehe [[Eiszeitalter|Eiszeit]], [[Milanković-Zyklen]]). Dieser Zyklus ist jedoch hauptsächlich durch die raschere Bewegung des Frühlingspunkts bestimmt. Der Winkel zwischen dem Perihel und einem (unendlich weit entfernt gedachten) Fixstern ändert sich dagegen nur mit einer Rate von 0,323°/Jahrhundert, so dass das Perihel etwa 110.000 Jahre braucht, um bezüglich des [[Inertialsystem|inertialen Raums]] einmal die Erdbahn zu umrunden. Dies ist die Rate der Perihelbewegung, wie sie durch äußere Störeinflüsse verursacht wird. | Die Zahlenwerte beider Spalten unterscheiden sich um 1,396° pro Jahrhundert, die Rate der [[Präzession]] der Erde in ekliptikaler Länge. So ändert sich zum Beispiel der Winkel zwischen dem Perihel der Erde und dem Frühlingspunkt um 1,720°/Jahrhundert, so dass beide nach circa 21.000 Jahren wieder dieselbe Stellung zueinander einnehmen, was unter anderem Auswirkungen auf das Klima haben könnte (siehe [[Eiszeitalter|Eiszeit]], [[Milanković-Zyklen]]). Dieser Zyklus ist jedoch hauptsächlich durch die raschere Bewegung des Frühlingspunkts bestimmt. Der Winkel zwischen dem Perihel und einem (unendlich weit entfernt gedachten) Fixstern ändert sich dagegen nur mit einer Rate von 0,323°/Jahrhundert, so dass das Perihel etwa 110.000 Jahre braucht, um bezüglich des [[Inertialsystem|inertialen Raums]] einmal die Erdbahn zu umrunden. Dies ist die Rate der Perihelbewegung, wie sie durch äußere Störeinflüsse verursacht wird. | ||
Der Erde-Mond-Schwerpunkt durchläuft das Perihel gegenwärtig am 3. oder 4. Januar, das Aphel am 4. oder 5. Juli. Um das Jahr 1600 war die größte Sonnennähe der Erde zwischen 26. und 28. Dezember. Um das Jahr 2500 herum wird sie auf den 10. bis 13. Januar fallen.<ref>[http://astropixels.com/ephemeris/perap/perap1501.html Earth at Perihelion and Aphelion: 1501 to 1600] ... [http://astropixels.com/ephemeris/perap2001.html Earth at Perihelion and Aphelion: 2001 to 2100] ... [http://astropixels.com/ephemeris/perap/perap2401.html Earth at Perihelion and Aphelion: 2401 to 2500] von Fred Espenak (astropixels.com), abgerufen am 8. Juli 2021</ref> | |||
Das Ausmaß der Periheldrehung hängt unter anderem auch von der Exzentrizität der betreffenden Bahn ab. Die Venus mit ihrer beinahe kreisförmigen Bahn weist daher eine auffallend geringe siderische Periheldrehung auf. | Das Ausmaß der Periheldrehung hängt unter anderem auch von der Exzentrizität der betreffenden Bahn ab. Die Venus mit ihrer beinahe kreisförmigen Bahn weist daher eine auffallend geringe siderische Periheldrehung auf. | ||
| Zeile 142: | Zeile 145: | ||
:: mit ''T'' [[Julianisches Jahrhundert|JJhd]] seit [[J1900.5]] | :: mit ''T'' [[Julianisches Jahrhundert|JJhd]] seit [[J1900.5]] | ||
Der Zyklus findet sich in der Variation der [[Lunation]]en | Der Zyklus findet sich in der Variation der [[Lunation]]en und ist auch als Periode der [[Gezeiten]] und meteorologischer Phänomene wohluntersucht.<ref name="apse caycle">Erste Forschungen von {{Literatur |Autor=Otto Pettersson |Titel=On the occurrence of lunar periods in solar activity and the climate of the earth. A study in geophysics and cosmic physics |Sammelwerk=Svenska Hydrogr. Biol. Komm |Datum=1914 |Sprache=en}}; {{Literatur |Autor=derslb. |Hrsg=Conseil Permanente International pour l’Exploration de la Mer |Titel=Long periodical variations of the tide-generating force |Sammelwerk=Pub. Circ. |Nummer=65 |Datum= |Seiten=2–23 |Sprache=en}}; zitiert n. und weitere Literatur: {{Literatur |Autor=John E. Sanders (Barnard College, Columbia University) |Titel=The Lunar Perigee-syzygy Cycle for 1998: Implications for Astronomic Tidal Heights |Datum= |Sprache=en |Online=[http://pbisotopes.ess.sunysb.edu/lig/Conferences/Abstracts98/Sanders.pdf ess.sunysb.edu] |Format=PDF |KBytes= |Abruf=2010-05-09}}; {{Literatur |Autor=derslb. |Titel=Lunar Cycles – 1999 |Datum= |Sprache=en |Online=[http://www.geo.sunysb.edu/lig/Conferences/abstracts99/Sanders_lunar_ms.pdf geo.sunysb.edu] |Format=PDF |KBytes=}}</ref> | ||
=== Künstliche Erdsatelliten === | === Künstliche Erdsatelliten === | ||
| Zeile 149: | Zeile 152: | ||
Beschreibt man die Abweichung des Erdgravitationspotentials von der Kugelgestalt vereinfacht durch Beschränkung auf sein Quadrupolmoment <math>J_2</math>, so beträgt die Bewegung des Perigäums <math>\omega</math><ref name="Hofmann-Wellenhof 1997 S. 62" /> | Beschreibt man die Abweichung des Erdgravitationspotentials von der Kugelgestalt vereinfacht durch Beschränkung auf sein Quadrupolmoment <math>J_2</math>, so beträgt die Bewegung des Perigäums <math>\omega</math><ref name="Hofmann-Wellenhof 1997 S. 62" /> | ||
: <math>\dot \omega = \frac{3}{4} \, n \, a_E^2 \, \frac{5 \cos^ | : <math>\dot \omega = \frac{3}{4} \, n \, a_E^2 \, \frac{5 \cos^2(i)-1}{a^2 (1-e^2)^2} \, J_2</math> | ||
{| | {| | ||
| Zeile 168: | Zeile 171: | ||
|- | |- | ||
|<math>J_2</math> | |<math>J_2</math> | ||
| | |[[Geoid#Geoid-Näherungen mit Kugelfunktionen|Entwicklungskoeffizient des Quadrupolmoments]] des Gravitationspotentials der Erde (1,0826359·10<sup>−3</sup>)<ref>International Earth Rotation & Reference Systems Service: ''[http://hpiers.obspm.fr/eop-pc/models/constants.html Useful Constants]'', aufgerufen am 15. August 2006</ref> | ||
|} | |} | ||
| Zeile 174: | Zeile 177: | ||
=== Relativistische Periheldrehung === | === Relativistische Periheldrehung === | ||
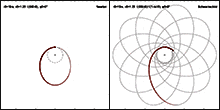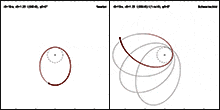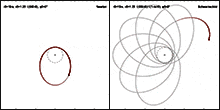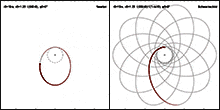
[[Datei: | [[Datei:Newton versus Schwarzschild trajectories-thumbnail.gif|mini|verweis=Datei:Newton_versus_Schwarzschild_trajectories.gif|Periheldrehung eines Testpartikels im starken gravitativen Feld einer nichtrotierenden zentralen Masse.]] | ||
[[Datei: | [[Datei:Horizon skimming Kerr orbit thumbnail.gif|mini|verweis=Datei:Horizon_skimming_Kerr_orbit.gif|Testpartikel im starken gravitativen Feld einer schnell rotierenden zentralen Masse.]] | ||
Der relativistische Anteil an der Periheldrehung konnte neben Merkur auch bei der [[Venus (Planet)|Venus]], der [[Erde]], dem [[Mars (Planet)|Mars]] sowie dem Asteroiden [[(1566) Icarus|Icarus]] nachgewiesen werden (siehe Tabelle,<ref>(Nobili 1986), zitiert nach (Dehnen 1988)</ref> Stand 1986). Bei der [[Erdbahn|Erde]] beispielsweise beträgt die gesamte beobachtete Drehung 1161″ je Jahrhundert; das ist um 5″ mehr, als nach der newtonschen Gravitationstheorie zu erwarten ist. Dieser Überschuss ist gut verträglich mit der relativistischen Vorhersage von 3,8″. | Der relativistische Anteil an der Periheldrehung konnte neben Merkur auch bei der [[Venus (Planet)|Venus]], der [[Erde]], dem [[Mars (Planet)|Mars]] sowie dem Asteroiden [[(1566) Icarus|Icarus]] nachgewiesen werden (siehe Tabelle,<ref>(Nobili 1986), zitiert nach (Dehnen 1988)</ref> Stand 1986). Bei der [[Erdbahn|Erde]] beispielsweise beträgt die gesamte beobachtete Drehung 1161″ je Jahrhundert; das ist um 5″ mehr, als nach der newtonschen Gravitationstheorie zu erwarten ist. Dieser Überschuss ist gut verträglich mit der relativistischen Vorhersage von 3,8″. | ||
{| class="wikitable" | {| class="wikitable" | ||
| | ! rowspan="2" |Körper | ||
! colspan="2" | Drehung pro Jhdt<br /><small>relativistischer Anteil</small> | |||
|- | |||
!Theorie | !Theorie | ||
!Beobachtung | !Beobachtung | ||
| Zeile 188: | Zeile 193: | ||
|- | |- | ||
|Venus | |Venus | ||
|8,6″ | |{{0}}8,6″ | ||
|8,4″ ± 4,8″ | |{{0}}8,4″{{0}} ± 4,8″ | ||
|- | |- | ||
|Erde | |Erde | ||
|3,8″ | |{{0}}3,8″ | ||
|5,0″ ± 1,2″ | |{{0}}5,0″{{0}} ± 1,2″ | ||
|- | |- | ||
|Mars | |Mars | ||
|1,4″ | |{{0}}1,4″ | ||
|1,5″ ± 0,15″ | |{{0}}1,5″{{0}} ± 0,15″ | ||
|- | |- | ||
|Icarus | |Icarus | ||
|10,3″ | |10,3″ | ||
|9,8″ ± 0,8″ | |{{0}}9,8″{{0}} ± 0,8″ | ||
|} | |} | ||
| Zeile 211: | Zeile 216: | ||
|<math>G \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | |<math>G \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | ||
|[[Gravitationskonstante|Newtonsche Gravitationskonstante]] | |[[Gravitationskonstante|Newtonsche Gravitationskonstante]] | ||
| | | | ||
|<math>M_\odot</math> | |<math>M_\odot</math> | ||
|[[Sonnenmasse]] | |[[Sonnenmasse]] | ||
|- | |- | ||
|<math>k \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | |<math>k \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | ||
|[[Gaußsche Gravitationskonstante]]: 0, | |[[Gaußsche Gravitationskonstante]]: {{nowrap|0,0172021 AE<sup>3/2</sup>d<sup>−1</sup>''M''<sub>☉</sub><sup>−1/2</sup>}} | ||
| | | | ||
|<math>D \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | |<math>D \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | ||
|Anzahl der Sekunden im Tag: 86400 s | |Anzahl der Sekunden im Tag: 86400 s | ||
|- | |- | ||
|<math>A \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | |<math>A \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | ||
|[[Astronomische Einheit]] in Metern: 1, | |[[Astronomische Einheit]] in Metern: AE = 1,49598·10<sup>11</sup> m | ||
| | | | ||
|<math>c \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | |<math>c \,</math> <!-- \, erzwingt großes Rendern, bitte drin lassen --> | ||
| Zeile 242: | Zeile 247: | ||
|Periheldrehung, Radiant pro Jahr | |Periheldrehung, Radiant pro Jahr | ||
| | | | ||
| | | | ||
| | | | ||
|} | |} | ||
| Zeile 251: | Zeile 256: | ||
=== Exotische Systeme === | === Exotische Systeme === | ||
In extremer Form tritt die Apsidendrehung zwischen besonders massereichen Himmelskörpern wie [[Stern]]en und [[Neutronenstern]]en auf. Im Doppelpulsar [[PSR | In extremer Form tritt die Apsidendrehung zwischen besonders massereichen Himmelskörpern wie [[Stern]]en und [[Neutronenstern]]en auf. Im Doppelpulsar [[PSR J1915+1606]] beträgt die relativistische Periheldrehung 4,2° pro Jahr,<ref>(Sivaram 1995), (Will 2006) Kap. 5</ref> im Doppelsystem [[PSR J1906+0746]] beträgt sie 7,57° pro Jahr,<ref>(Lorimer 2006), (Will 2006) Kap. 5</ref> und in [[PSR J0737-3039]] (in dem beide Komponenten Pulsare sind) sogar 16,90° pro Jahr.<ref>(Burgay 2003), (Will 2006) Kap. 5, (Kramer 2006)</ref> | ||
Die [[Lichtkurve]] des Quasars [[OJ 287]] lässt vermuten, dass sich in seinem Zentrum zwei einander umkreisende [[Schwarzes Loch|Schwarze Löcher]] befinden, deren gegenseitiger Orbit sich pro 12-jährigem Umlauf um 39° dreht.<ref>M.J. Valtonen et al.: ''Confirmation of the Gravitational Wave Energy Loss in the Binary Black Hole System OJ287''. American Astronomical Society, AAS Meeting #211, #112.07 (2007), {{bibcode|2007AAS...21111207V}}</ref> | Die [[Lichtkurve]] des Quasars [[OJ 287]] lässt vermuten, dass sich in seinem Zentrum zwei einander umkreisende [[Schwarzes Loch|Schwarze Löcher]] befinden, deren gegenseitiger Orbit sich pro 12-jährigem Umlauf um 39° dreht.<ref>M.J. Valtonen et al.: ''Confirmation of the Gravitational Wave Energy Loss in the Binary Black Hole System OJ287''. American Astronomical Society, AAS Meeting #211, #112.07 (2007), {{bibcode|2007AAS...21111207V}}</ref> | ||
| Zeile 260: | Zeile 265: | ||
* (al-Battani 900): M. al-Battani: ''Zij''. Ar-Raqqah, ca. 900; lat. Übersetzung: C.A. Nallino: ''Al-Battani sive Albatenii Opus Astronomicum''. Mailand 1899–1907; Nachdruck Olms, Hildesheim 1977 | * (al-Battani 900): M. al-Battani: ''Zij''. Ar-Raqqah, ca. 900; lat. Übersetzung: C.A. Nallino: ''Al-Battani sive Albatenii Opus Astronomicum''. Mailand 1899–1907; Nachdruck Olms, Hildesheim 1977 | ||
* (Anderson 1987): J.D. Anderson, G. Colombo, P.B. Espsitio, E.L. Lau, G.B. Trager: ''The mass, gravity field, and ephemeris of Mercury''. In: ''Icarus'', 71, 1987, S. 337 | * (Anderson 1987): J.D. Anderson, G. Colombo, P.B. Espsitio, E.L. Lau, G.B. Trager: ''The mass, gravity field, and ephemeris of Mercury''. In: ''Icarus'', 71, 1987, S. 337 | ||
* (Anderson 1991): J.D. Anderson, M.A. Slade, R.F. Jurgens, E.L. Lau, X.X. Newhall, E.M. Standish Jr.: ''Radar and Spacecraft Ranging to Mercury between 1966 and 1988''. In: ''Proc. ASA'', 9, 1991, S. 324 | * (Anderson 1991): J.D. Anderson, M.A. Slade, R.F. Jurgens, E.L. Lau, X.X. Newhall, [[E. Myles Standish|E.M. Standish Jr.]]: ''Radar and Spacecraft Ranging to Mercury between 1966 and 1988''. In: ''Proc. ASA'', 9, 1991, S. 324 | ||
* (Anderson 1992): J.D. Anderson et al.: ''Recent Developments in Solar-System Tests of General Relativity''. In: H. Sato, T. Nakamura (Hrsg.): ''Proc. Sixth Marcel Grossmann Meeting''. World Scientific, Singapore (1992) | * (Anderson 1992): J.D. Anderson et al.: ''Recent Developments in Solar-System Tests of General Relativity''. In: H. Sato, T. Nakamura (Hrsg.): ''Proc. Sixth Marcel Grossmann Meeting''. World Scientific, Singapore (1992) | ||
* (Burgay 2003): M. Burgay: ''An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system''. In: ''Nature'', 426, 2003, S. 531–533, [http://www.nature.com/nature/journal/v426/n6966/abs/nature02124.html Abstract], {{arXiv|astro-ph/0312071}} | * (Burgay 2003): M. Burgay: ''An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system''. In: ''Nature'', 426, 2003, S. 531–533, [http://www.nature.com/nature/journal/v426/n6966/abs/nature02124.html Abstract], {{arXiv|astro-ph/0312071}} | ||
* (Dehnen 1988): H. Dehnen: ''Empirische Grundlagen und experimentelle Prüfung der Relativitätstheorie''. In: J. Audretsch, K. Mainzer (Hrsg.): ''Philosophie und Physik der Raumzeit''. Grundlagen der exakten Naturwissenschaften, | * (Dehnen 1988): H. Dehnen: ''Empirische Grundlagen und experimentelle Prüfung der Relativitätstheorie''. In: J. Audretsch, K. Mainzer (Hrsg.): ''Philosophie und Physik der Raumzeit''. Grundlagen der exakten Naturwissenschaften, Band 7. BI-Wissenschaftsverlag 1988 | ||
* (Einstein 1915): A. Einstein: ''Erklärung der Perihelbewegung des Merkur aus der Allgemeinen Relativitätstheorie''. In: ''Sitzungsberichte der Preußischen Akademie der Wissenschaften'', 1915, S. 831–839 | * (Einstein 1915): A. Einstein: ''Erklärung der Perihelbewegung des Merkur aus der Allgemeinen Relativitätstheorie''. In: ''Sitzungsberichte der Preußischen Akademie der Wissenschaften'', 1915, S. 831–839 | ||
* (Freundlich 1915): E. Freundlich: ''Über die Erklärung der Anomalien im Planeten-System durch die Gravitationswirkung interplanetarer Massen''. In: Astronomische Nachrichten Nr. 4803, Bd. 201, 1915, S. 49–56, {{bibcode|1915AN....201...49F}} | * (Freundlich 1915): E. Freundlich: ''Über die Erklärung der Anomalien im Planeten-System durch die Gravitationswirkung interplanetarer Massen''. In: Astronomische Nachrichten Nr. 4803, Bd. 201, 1915, S. 49–56, {{bibcode|1915AN....201...49F}} | ||
* (Guthmann 2000): A. Guthmann: ''Einführung in die Himmelsmechanik und Ephemeridenrechnung''. 2. Auflage. Spektrum, Heidelberg 2000, ISBN 3-8274-0574-2 | * (Guthmann 2000): A. Guthmann: ''Einführung in die Himmelsmechanik und Ephemeridenrechnung''. 2. Auflage. Spektrum, Heidelberg 2000, ISBN 3-8274-0574-2 | ||
* (Hofmann-Wellenhof 1997): B. Hofmann-Wellenhof et al.: ''GPS | * (Hofmann-Wellenhof 1997): B. Hofmann-Wellenhof et al.: ''GPS – Theory and Practice''. 4. Auflage. Springer, Wien 1997, ISBN 3-211-82839-7 | ||
* (Kramer 2006): M. Kramer et al.: ''Tests of general relativity from timing the double pulsar''. In: ''Science Express'', 14. Sept. 2006, {{arXiv|astro-ph/0609417}} | * (Kramer 2006): M. Kramer et al.: ''Tests of general relativity from timing the double pulsar''. In: ''Science Express'', 14. Sept. 2006, {{arXiv|astro-ph/0609417}} | ||
* (Lorimer 2006): D.R. Lorimer et al.: ''Arecibo Pulsar Survey Using ALFA. II. The Young, Highly Relativistic Binary Pulsar J1906+0746''. In: ''ApJ'', 640, 2006, S. 428–434 ([http://www.journals.uchicago.edu/ApJ/journal/issues/ApJ/v640n1/63810/brief/63810.abstract.html Abstract]) | * (Lorimer 2006): D.R. Lorimer et al.: ''Arecibo Pulsar Survey Using ALFA. II. The Young, Highly Relativistic Binary Pulsar J1906+0746''. In: ''ApJ'', 640, 2006, S. 428–434 ([http://www.journals.uchicago.edu/ApJ/journal/issues/ApJ/v640n1/63810/brief/63810.abstract.html Abstract]) | ||
* (Meeus 2000): J. Meeus: ''Astronomical Algorithms''. 2nd ed., 2nd prnt., Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1 | * (Meeus 2000): J. Meeus: ''Astronomical Algorithms''. 2nd ed., 2nd prnt., Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1 | ||
* (Morrison Ward 1975): L.V. Morrison, C.G. Ward: ''An Analysis of the Transits of Mercury: 1677–1973''. In: ''Mon. Not. R. astr. Soc.'', 173, 1975, S. | * (Morrison Ward 1975): L.V. Morrison, C.G. Ward: ''An Analysis of the Transits of Mercury: 1677–1973''. In: ''Mon. Not. R. astr. Soc.'', 173, 1975, S. 183–206, {{bibcode|1975MNRAS.173..183M}} | ||
* (Neugebauer 1975): O. Neugebauer: ''A History of Ancient Mathematical Astronomy''. Springer, Berlin 1975, ISBN 3-540-06995-X | * (Neugebauer 1975): O. Neugebauer: ''A History of Ancient Mathematical Astronomy''. Springer, Berlin 1975, ISBN 3-540-06995-X | ||
* (Nobili 1986): A. Nobili, C. Will: ''The real value of Mercury’s perihelion advance''. In: ''Nature'', 320, 1986, S. 39–41, {{bibcode|1986Natur.320...39N}} | * (Nobili 1986): A. Nobili, C. Will: ''The real value of Mercury’s perihelion advance''. In: ''Nature'', 320, 1986, S. 39–41, {{bibcode|1986Natur.320...39N}} | ||
| Zeile 291: | Zeile 296: | ||
* (Sivaram 1995): C. Sivaram: ''The Hulse-Taylor binary pulsar PSR1913+16''. In: ''Bull. Astr. Soc. India'', 23, 1995, S. 77–83, {{bibcode|1995BASI...23...77S}} | * (Sivaram 1995): C. Sivaram: ''The Hulse-Taylor binary pulsar PSR1913+16''. In: ''Bull. Astr. Soc. India'', 23, 1995, S. 77–83, {{bibcode|1995BASI...23...77S}} | ||
* (Will 1993): C.M. Will: ''Theory and Experiment in Gravitational Physics''. Revised edition, Cambridge University Press, Cambridge 1993, ISBN 0-521-43973-6 | * (Will 1993): C.M. Will: ''Theory and Experiment in Gravitational Physics''. Revised edition, Cambridge University Press, Cambridge 1993, ISBN 0-521-43973-6 | ||
* (Will 2006): C.M. Will: ''The Confrontation Between General Relativity and Experiment''. In: ''Living Rev. Relativity'', 9, 2006, | * (Will 2006): C.M. Will: ''The Confrontation Between General Relativity and Experiment''. In: ''Living Rev. Relativity'', 9, 2006, {{arXiv|gr-qc/0510072}} | ||
== Weblinks == | == Weblinks == | ||
Aktuelle Version vom 24. Februar 2022, 19:34 Uhr

Die Apsidendrehung einer elliptischen Umlaufbahn ist eine fortschreitende Drehung der ganzen Bahn in der Bahnebene. Dabei dreht sich die Apsidenlinie kontinuierlich, während Form und Ebene der Bahn im Raum gleich bleiben. Je nach Zentralkörper werden auch folgende Bezeichnungen verwendet:
- Periheldrehung, oder auch Präzession des Perihels, wenn die Bahn die Sonne umläuft und
- Perigäumsdrehung, wenn die Bahn die Erde umläuft, also das Perigäum betrachtet wird.
Wenn diese Bewegung gelegentlich als „Präzession“ des Perizentrums bezeichnet wird, darf sie nicht mit der ähnlich klingenden Präzession der Äquinoktien verwechselt werden, bei der es sich zwar ebenfalls um eine Bahnstörung handelt, bei der jedoch die Lage einer Ebene im Raum betroffen ist.
Ursachen
Eine Apsidendrehung entsteht, wenn ein Himmelskörper auf seiner elliptischen Umlaufbahn um einen Zentralkörper bestimmten äußeren Störungen unterliegt. Wäre der Himmelskörper einer Anziehungskraft ausgesetzt, welche streng umgekehrt quadratisch mit der Entfernung vom Zentralkörper abnimmt, so würde er sich exakt auf einer Keplerellipse bewegen, deren Form, Lage und Orientierung im Raum unverändert blieben. Nach dem Satz von Bertrand sind die einzigen zentralsymmetrischen Potentiale mit geschlossenen Bahnen das 1/r-Potential und das Potential des harmonischen Oszillators mit radialem Funktionsverlauf proportional r2. Abweichungen vom streng umgekehrt-quadratischen Kraftgesetz führen jedoch zu verschiedenen Arten von Bahnstörungen, welche Form, Lage und Orientierung der Bahn verändern können. Eine dieser Bahnstörungen ist die Apsidendrehung.
- Eine mögliche Ursache für Abweichungen vom 1/r2-Zentralkraftgesetz ist die Gegenwart anderer Körper, welche zusätzliche Gravitationskräfte auf den betrachteten Himmelskörper ausüben. Im Falle der Planetenbahnen ist der Einfluss der jeweils anderen Planeten die Hauptursache für die Periheldrehungen.
- Eine andere Ursache kann in Abweichungen des Zentralkörpers von der Kugelform liegen. Während ein exakt kugelsymmetrisch aufgebauter ausgedehnter Körper dasselbe streng invers-quadratische Gravitationsfeld erzeugen würde wie ein punktförmiger Körper derselben Masse, führen unregelmäßige Masseverteilungen oder der Äquatorwulst abgeplatteter Zentralkörper zu Abweichungen vom invers-quadratischen Kraftgesetz und damit zu Bahnstörungen. Der Äquatorwulst der Erde verursacht (neben anderen Bahnstörungen) Perigäumsdrehungen bei künstlichen Erdsatelliten. Die Abplattung der Sonne verursacht Periheldrehungen der Planetenbahnen, welche wegen der Geringfügigkeit der Abplattung und des großen Abstandes der Planeten jedoch wesentlich kleiner sind als die von den Planeten untereinander verursachten Drehungen.
- Die Krümmung der Raumzeit, ein Effekt der Allgemeinen Relativitätstheorie, bewirkt eine Abweichung von den Newtonschen Bewegungsgleichungen (siehe Effektives Potential#Allgemeine Relativitätstheorie). Dadurch entsteht ein Beitrag zur Periheldrehung, der Schwarzschild-Präzession genannt wird.
- Es gibt Hypothesen, dass das idealisierte Kraftgesetz selbst vom invers-quadratischen Verhalten abweicht (z. B. die Modifizierte Newtonsche Dynamik). Dies würde ebenfalls zur Apsidendrehung beitragen.
Aus all diesen Ursachen resultiert – in einem bezüglich des Fixsternhintergrunds ruhenden Koordinatensystem – eine rosettenartige Bewegung des Körpers: Die anomalistische Periode entspricht nicht genau der siderischen. Himmelsmechanisch wird das durch einen langperiodischen Term des Bahnelements Argument des Perizentrums beschrieben.
Wird die Bahn nicht in einem bezüglich des Fixsternhintergrunds ruhenden Bezugssystem beschrieben, sondern in einem rotierenden Bezugssystem, so kommt zu den oben beschriebenen physikalisch verursachten Drehungen eine zusätzliche scheinbare Drehung hinzu, welche lediglich die Drehung des Bezugssystems widerspiegelt. Im Falle der Planetenbahnen des Sonnensystems betragen die Periheldrehungen – von einem fest gewählten Frühlingspunkt aus gezählt – nur Bruchteile eines Grades pro Jahrhundert. Werden die Bahnen hingegen bezüglich des beweglichen Äquinoktiums des Datums beschrieben, so sind ihre Geschwindigkeiten in diesem rotierenden Bezugssystem um die Präzessionsgeschwindigkeit des Frühlingspunkts, nämlich 1,396° pro Jahrhundert, höher und liegen zwischen 1° und 2° pro Jahrhundert.
Episoden aus der Forschungsgeschichte
Bewegung der Apogäen
Bereits den antiken Astronomen war durch Beobachtung bekannt, dass Sonne, Mond und Planeten ihre Bahnen nicht mit konstanten Geschwindigkeiten durchlaufen. Griechische Astronomen berücksichtigten dies in ihren Planetentheorien, indem sie den Mittelpunkt der jeweiligen als kreisförmig vorausgesetzten Planetenbahn nicht mit dem Mittelpunkt der im Zentrum des Universums angenommenen Erde zusammenfallen ließen, sondern in geeigneter Richtung um einen bestimmten Betrag (die so genannte Exzentrizität, nicht zu verwechseln mit der Exzentrizität einer Ellipsenbahn) versetzten. Auf der dem Beobachter näher liegenden Bahnhälfte bewegte sich der gleichmäßig laufende Planet nun scheinbar schneller als auf der gegenüberliegenden Hälfte. Wie sich zeigen lässt, kann der reale, dem 2. Keplerschen Gesetz folgende Geschwindigkeitsverlauf eines Planeten in sehr guter Näherung mittels einer geeignet verschobenen Kreisbahn (einem so genannten Exzenter) rechnerisch nachvollzogen werden. Hipparchos beispielsweise schloss aus den ungleichen Längen der Jahreszeiten auf die Geschwindigkeitsvariation der (damals als Planet behandelten) Sonne in den einzelnen Bahnquadranten und beschrieb ihren Umlauf durch einen Kreis, welcher um 1/24 seines Radius in Richtung 65,5° verschoben war.[1] In dieser Richtung lag also auch das Apogäum der Sonnenbahn, dessen ekliptikale Länge damals auch tatsächlich 66,23° betrug.[2] (Damals wurde das Apogäum als Bezugspunkt benutzt, während man heute das Perigäum bevorzugt.)
Ptolemäus wiederholte die Bahnbestimmung 300 Jahre später. Da seine Beobachtungen aber dieselben Längen für die Jahreszeiten ergaben, erhielt er auch dieselbe Sonnenbahn und hielt daher die Lage ihres Apogäums für unveränderlich bezüglich der Äquinoktialpunkte:
„Auch wir gelangen zu dem Ergebnis, dass noch heutzutage die Zeiten der obenbezeichneten Quadranten und die angegebenen Verhältnisse nahezu dieselben sind, woraus uns ersichtlich wird, dass der Exzenter der Sonne zu den Wende- und Nachtgleichenpunkten ewig dieselbe Lage bewahrt.“[3]
Anders verhielten sich jedoch die Apogäen der übrigen Planeten. Aus den Ergebnissen zahlreicher Beobachtungen und Auswertungen schloss er, dass deren Apogäen nicht bezüglich der Äquinoktialpunkte, sondern bezüglich der Fixsterne ruhen. Dies ist insofern bemerkenswert, als seiner Auffassung nach (und im Gegensatz zum heutigen Standpunkt) die Äquinoktialpunkte als ruhend und die Fixsterne als infolge der Präzession bewegt betrachtet wurden. Entsprechend hielt er die Apogäen für beweglich, und ihre Geschwindigkeit musste bestimmt werden. Die Beobachtungen zeigten ihm, dass sie sich alle etwa gleich schnell rechtläufig bewegten und dass ihre Geschwindigkeit im Rahmen der Beobachtungsgenauigkeit mit der Präzessionsgeschwindigkeit der Fixsterne übereinstimmte; er fand, dass
„auch die Apogeen der Exzenter einen ganz geringen von den Wendepunkten aus in der Richtung der Zeichen vor sich gehenden Fortschritt bewerkstelligen, welcher wieder gleichförmig um den Mittelpunkt der Ekliptik verläuft und für alle Planeten ungefähr ebensogroß ist, wie er an der Fixsternsphäre wahrgenommen worden ist – d. h. in 100 Jahren vom Betrage eines Grades -, soweit es wenigstens möglich ist, aus dem vorliegenden Material einen Einblick zu gewinnen.“[4]
Im 9. Jahrhundert bemerkte Thabit ibn Qurrah, dass auch das Sonnenapogäum eine rechtläufige Bewegung bezüglich der Äquinoktialpunkte ausführte.[5] Man hielt diese Bewegung zunächst aber noch wie die der Planetenapogäen für rein präzessionsbedingt. Al-Battani beispielsweise legte das Sonnenapogäum für den 1. März 880 auf 82° 15' ekliptikaler Länge und gab die Anweisung, zur Berechnung der Apogäumslänge zu anderen Zeitpunkten für jeweils 66 verstrichene Jahre 1° Präzessionsverschiebung zu addieren oder abzuziehen:
„Das Apogäum bewegt sich nämlich mit derselben Bewegung, mit der sich die Fixsternsphäre dreht und von welcher wir durch Beobachtung festgestellt haben, dass sie in 66 römischen Jahren 1 Grad beträgt.“[6]
Dasselbe galt für ihn, wie auch schon für Ptolemäus, für die Apogäen der Planeten:
„Die [Längen dieser] Apogäen bewegen sich mit der Bewegung der Fixsternsphäre, nämlich ein Grad in 66 Sonnenjahren.“[7]
Erst Ibn asch-Schatir stellte im 14. Jahrhundert durch Beobachtung fest, dass das Sonnenapogäum nicht genau mit der Geschwindigkeit der Präzession wanderte (nämlich mit 1° pro 60 Persischen Jahren gegenüber 1° pro 70 Persischen Jahren), sich also bezüglich der Fixsterne eigenständig bewegte.[8]
Im Gegensatz zu den Planetenbahnen war die Perigäumsdrehung des Mondes bereits den babylonischen Astronomen bekannt und explizit in ihren Rechenschemata berücksichtigt.[9] Hipparch und Ptolemäus übernahmen aus der babylonischen Astronomie grundlegende Zahlenwerte und arbeiteten sie zu detaillierten Mondtheorien auf Basis des Epizykelmodells aus.[10]
Periheldrehung des Merkur
Die elliptische Gestalt der Planetenbahnen wurde 1609 zunächst empirisch durch die Keplerschen Gesetze beschrieben. Die physikalische Begründung folgte erst Mitte des 17. Jahrhunderts mit der Himmelsmechanik von Isaac Newton. Mit seinem universellen Kraftgesetz, das auch die Gravitation beschreibt, war es möglich geworden, die Bahnstörungen näher zu untersuchen, die die Planeten wechselseitig verursachen. Insbesondere konnten die beobachteten Apsidendrehungen der Planeten und des Mondes praktisch vollständig durch Newtons Theorie erklärt werden.
In der Mitte des 19. Jahrhunderts jedoch benutzte Urbain Le Verrier Beobachtungen von Merkurdurchgängen für eine besonders genaue Vermessung der Merkurbahn und stellte anhand der verbesserten Daten fest, dass die Periheldrehung des Merkur etwas stärker ausfiel als erwartet. Nach den himmelsmechanischen Berechnungen sollte sie etwa 530″ (Bogensekunden) pro Jahrhundert betragen, wobei circa 280″ auf den Einfluss der Venus entfallen, circa 150″ auf Störungen durch Jupiter und circa 100″ auf die restlichen Planeten.[11] Die beobachtete Periheldrehung (moderner Wert: 571,91″/Jahrhundert[12]) war jedoch deutlich größer; der moderne Wert für die Diskrepanz beträgt 43,11″.
Le Verrier, der durch die Untersuchung unerklärter Anteile in den Bahnstörungen des Uranus bereits erfolgreich die Entdeckung Neptuns ermöglicht hatte, vermutete als Ursache der Diskrepanz bei Merkur eine Störung durch einen bislang unbekannten Planeten auf einer Bahn innerhalb der Merkurbahn. Dieser Planet erhielt den Namen Vulkan, konnte jedoch trotz ausgedehnter Suche – unter anderem während mehrerer Sonnenfinsternisse – nicht entdeckt werden. Ebenso konnte auch kein für die Störungen verantwortlicher sonnennaher Asteroidengürtel nachgewiesen werden. Andere verdächtigten den für das Zodiakallicht verantwortlichen Staubgürtel oder sahen zumindest einen Teil der Ursache in einer wegen ihrer Rotation abgeplatteten Gestalt der Sonne (siehe auch unten), blieben mit ihren Erklärungsversuchen aber letztlich ebenfalls erfolglos.[13]
Weitere Erklärungsversuche zogen die Gültigkeit des Newtonschen Kraftgesetzes in Zweifel. So gelang es unter Zugrundelegung von elektrodynamischen Kraftgesetzen zum Beispiel Levy (1890) und vor allem Paul Gerber (1898), den Überschuss vollständig abzuleiten, unter der Voraussetzung, dass die Ausbreitungsgeschwindigkeit der Gravitation gleich der Lichtgeschwindigkeit ist. Gerbers Formel für die Perihelabweichung war formal bereits identisch mit der später von Einstein aufgestellten. Jedoch waren die zugrunde gelegten Kraftgesetze falsch und die Theorien dieser Art mussten verworfen werden.[14][15]
Erst die Allgemeine Relativitätstheorie (ART) von Albert Einstein, die die Gravitation als Krümmung der Raumzeit beschreibt, auf deren Struktur auch die Weltkörper ihrerseits Einfluss haben, konnte den Überschuss überzeugend erklären.[16] Dieser Erfolg gilt als eine der Hauptstützen der Allgemeinen Relativitätstheorie und als ihre erste große Bestätigung. Der relativistisch berechnete Anteil von 42,98″[17] stimmt sehr gut mit dem beobachteten Überschuss von 43,11″ überein. Die Ursache für den relativistischen Effekt liegt in der geringfügigen Abweichung des relativistisch behandelten Gravitationsfelds vom streng invers-quadratischen Verhalten.[18]
Die Übereinstimmung zwischen Beobachtung und relativistischer Rechnung würde weniger gut ausfallen, wenn ein merklicher Teil des beobachteten Überschusses auf eine rotationsbedingte Abplattung der Sonne zurückzuführen wäre und der übrigbleibende zu erklärende Anteil daher deutlich geringer wäre als gemäß ART berechnet. Versuche, die äußerst geringe Abplattung der Sonne zu messen, lieferten über lange Zeit hinweg widersprüchliche Ergebnisse, sodass auch stets ein wenig zweifelhaft blieb, wie gut die Übereinstimmung der relativistischen Vorhersage mit der Beobachtung tatsächlich war. Helioseismologische Untersuchungen haben jedoch mittlerweile das Quadrupolmoment $ J_{2} $ der Sonne zuverlässig zu (2,18 ± 0,06)·10−7 bestimmt; dieses Quadrupolmoment liefert nur einen Beitrag von einigen Hundertstel Bogensekunden zur Periheldrehung und ist daher vernachlässigbar.[19] Eine andere Möglichkeit zur Bestimmung von $ J_{2} $ nutzt den Umstand, dass der relativistische und der $ J_{2} $-bedingte Anteil an der gesamten Periheldrehung mit wachsender Entfernung von der Sonne unterschiedlich rasch abfallen und sich so durch Vergleich der Gesamtdrehungen verschiedener Planeten voneinander trennen lassen. Eine solche Untersuchung[20] lieferte mit $ J_{2} $ = (1,9 ± 0,3)·10−7 ein Ergebnis, das nahe an dem der Helioseismologie liegt.
Die Tabelle führt einige Beobachtungsergebnisse der Periheldrehung aus den letzten Jahrzehnten auf:
| Jahr | Autoren | Methode | Drehung pro Jahrhundert | Quelle |
|---|---|---|---|---|
| 1975 | Morrison, Ward | Merkurdurchgänge | 41,9″ ± 0,5″ | [21] |
| 1976 | Shapiro u. a. | Radar | 43,11″ ± 0,21″ | [22] |
| 1987 | Anderson u. a. | Radar | 42,92″ ± 0,20″ | [23] |
| 1991 | Anderson u. a. | Radar | 42,94″ ± 0,20″ | [24] |
| 1992 | Anderson u. a. | Radar | 43,13″ ± 0,14″ | [25] |
Beispiele
Planetenbahnen
Die Bahnen aller Planeten des Sonnensystems unterliegen – hauptsächlich wegen ihrer gegenseitigen Störungen – kontinuierlichen Periheldrehungen in Richtung der Umlaufbewegung. Die folgende Tabelle[26] listet die Beträge dieser Drehungen sowohl bezüglich des Frühlingspunkts („tropisch“) als auch bezüglich des Fixsternhintergrunds („siderisch“) auf. Die Zahlenwerte sind langfristig leicht veränderlich und unterliegen auch geringfügigen kürzerfristigen Schwankungen. Die angegebenen Werte beschreiben die mittlere Bewegung (also unter Abrechnung der kurzfristigen Schwankungen) für den Beginn des Jahres 2000 (d. h. zur Epoche J2000.0).
| Planet | tropisch [°/Jh.] | siderisch [°/Jh.] |
|---|---|---|
| Merkur | 1,556 | 0,159 |
| Venus | 1,402 | 0,005 |
| Erde | 1,720 | 0,323 |
| Mars | 1,841 | 0,444 |
| Jupiter | 1,613 | 0,216 |
| Saturn | 1,964 | 0,567 |
| Uranus | 1,486 | 0,089 |
| Neptun | 1,426 | 0,029 |
Die Zahlenwerte beider Spalten unterscheiden sich um 1,396° pro Jahrhundert, die Rate der Präzession der Erde in ekliptikaler Länge. So ändert sich zum Beispiel der Winkel zwischen dem Perihel der Erde und dem Frühlingspunkt um 1,720°/Jahrhundert, so dass beide nach circa 21.000 Jahren wieder dieselbe Stellung zueinander einnehmen, was unter anderem Auswirkungen auf das Klima haben könnte (siehe Eiszeit, Milanković-Zyklen). Dieser Zyklus ist jedoch hauptsächlich durch die raschere Bewegung des Frühlingspunkts bestimmt. Der Winkel zwischen dem Perihel und einem (unendlich weit entfernt gedachten) Fixstern ändert sich dagegen nur mit einer Rate von 0,323°/Jahrhundert, so dass das Perihel etwa 110.000 Jahre braucht, um bezüglich des inertialen Raums einmal die Erdbahn zu umrunden. Dies ist die Rate der Perihelbewegung, wie sie durch äußere Störeinflüsse verursacht wird.
Der Erde-Mond-Schwerpunkt durchläuft das Perihel gegenwärtig am 3. oder 4. Januar, das Aphel am 4. oder 5. Juli. Um das Jahr 1600 war die größte Sonnennähe der Erde zwischen 26. und 28. Dezember. Um das Jahr 2500 herum wird sie auf den 10. bis 13. Januar fallen.[27]
Das Ausmaß der Periheldrehung hängt unter anderem auch von der Exzentrizität der betreffenden Bahn ab. Die Venus mit ihrer beinahe kreisförmigen Bahn weist daher eine auffallend geringe siderische Periheldrehung auf.
Mond
Die Apsidenlinie des Mondes dreht sich in 8,85 Jahren einmal um die gesamte Mondbahn. Die Hauptursache hierfür ist die Sonne, die als dritter, störender Körper auf den Umlauf des Mondes um die Erde einwirkt.[28]
Dieser Zyklus der Apsiden (englisch lunar apse cycle, perigee cycle) berechnet sich:[29]
- $ 360/(0{,}1114040803-0{,}0007739\cdot 2/10000\cdot T-0{,}00000026\cdot 3/10000\cdot T^{2})/365{,}25 $
- mit T JJhd seit J1900.5
Der Zyklus findet sich in der Variation der Lunationen und ist auch als Periode der Gezeiten und meteorologischer Phänomene wohluntersucht.[30]
Künstliche Erdsatelliten
Perigäumsdrehungen von Satelliten werden als grundlegendes Satellitenbahnelement dargestellt. Ihre Ursache liegt in der Abplattung der Erde und bei Satelliten in niedriger Umlaufbahn gegebenenfalls auch in der Atmosphärenreibung. Die Perigäumsdrehung der GPS-Satelliten, welche die Erde in einer Höhe von circa 20.200 Kilometern umkreisen, beträgt etwa 0,01° pro Tag.[31]
Beschreibt man die Abweichung des Erdgravitationspotentials von der Kugelgestalt vereinfacht durch Beschränkung auf sein Quadrupolmoment $ J_{2} $, so beträgt die Bewegung des Perigäums $ \omega $[31]
- $ {\dot {\omega }}={\frac {3}{4}}\,n\,a_{E}^{2}\,{\frac {5\cos ^{2}(i)-1}{a^{2}(1-e^{2})^{2}}}\,J_{2} $
| $ n $ | mittlere Bewegung des Satelliten |
| $ a_{E} $ | große Halbachse der Erde (6.378.137 m) |
| $ a $ | große Halbachse der Umlaufbahn |
| $ i $ | Neigung der Umlaufbahn |
| $ e $ | Exzentrizität der Umlaufbahn |
| $ J_{2} $ | Entwicklungskoeffizient des Quadrupolmoments des Gravitationspotentials der Erde (1,0826359·10−3)[32] |
Für Neigungen unter 63,4° bewegt sich das Perigäum in Bewegungsrichtung des Satelliten. Für Neigungen darüber bewegt es sich rückläufig. Hat der Satellit eine Bahnneigung von 63,4°, so unterliegt er (näherungsweise) keiner Perigäumsdrehung, denn $ 5\cos ^{2}(63{,}4^{\circ })-1=0 $. Beträgt seine Umlaufdauer darüber hinaus etwa 12 Stunden (genauer: einen halben siderischen Tag) und wählt man die Bahn sehr exzentrisch, so liegt das Apogäum während jedes Umlaufs längere Zeit über derselben Region der Erdoberfläche und der Satellit kann zum Beispiel günstig für Telekommunikationszwecke genutzt werden. Er befindet sich in einem so genannten Molnija-Orbit.
Relativistische Periheldrehung
Der relativistische Anteil an der Periheldrehung konnte neben Merkur auch bei der Venus, der Erde, dem Mars sowie dem Asteroiden Icarus nachgewiesen werden (siehe Tabelle,[33] Stand 1986). Bei der Erde beispielsweise beträgt die gesamte beobachtete Drehung 1161″ je Jahrhundert; das ist um 5″ mehr, als nach der newtonschen Gravitationstheorie zu erwarten ist. Dieser Überschuss ist gut verträglich mit der relativistischen Vorhersage von 3,8″.
| Körper | Drehung pro Jhdt relativistischer Anteil | |
|---|---|---|
| Theorie | Beobachtung | |
| Merkur | 42,98″ | 43,11″ ± 0,45″ |
| Venus | 8,6″ | 8,4″ ± 4,8″ |
| Erde | 3,8″ | 5,0″ ± 1,2″ |
| Mars | 1,4″ | 1,5″ ± 0,15″ |
| Icarus | 10,3″ | 9,8″ ± 0,8″ |
Für die relativistische Periheldrehung eines Planeten gilt:[17]
- $ {\dot {\omega }}={\frac {6\pi \,GM_{\odot }}{Pa(1-e^{2})c^{2}}}={\frac {6\pi k^{2}}{P{\bar {a}}(1-e^{2})}}{\frac {A^{2}}{D^{2}c^{2}}} $
| $ G\, $ | Newtonsche Gravitationskonstante | $ M_{\odot } $ | Sonnenmasse | |
| $ k\, $ | Gaußsche Gravitationskonstante: 0,0172021 AE3/2d−1M☉−1/2 | $ D\, $ | Anzahl der Sekunden im Tag: 86400 s | |
| $ A\, $ | Astronomische Einheit in Metern: AE = 1,49598·1011 m | $ c\, $ | Lichtgeschwindigkeit: 299792458 m/s | |
| $ a\, $ | große Halbachse des Planeten in Metern | $ {\bar {a}} $ | große Halbachse des Planeten in AE | |
| $ e\, $ | Exzentrizität der Planetenbahn | $ P\, $ | Bahnperiode des Planeten in Jahren | |
| $ {\dot {\omega }} $ | Periheldrehung, Radiant pro Jahr |
Die zweite Form der Gleichung ergibt sich, wenn die heliozentrische Gravitationskonstante $ GM_{\odot } $ durch die Gaußsche Gravitationskonstante $ k\, $ ausgedrückt wird.
Mit den Bahndaten $ {\bar {a}} $ = 0,387099 AE, $ e\, $ = 0,205630 und $ P\, $ = 0,24085 Jahre für Merkur erhält man zum Beispiel die in der Tabelle angegebene Periheldrehung von 42,98 Bogensekunden pro 100 Jahren.
Exotische Systeme
In extremer Form tritt die Apsidendrehung zwischen besonders massereichen Himmelskörpern wie Sternen und Neutronensternen auf. Im Doppelpulsar PSR J1915+1606 beträgt die relativistische Periheldrehung 4,2° pro Jahr,[34] im Doppelsystem PSR J1906+0746 beträgt sie 7,57° pro Jahr,[35] und in PSR J0737-3039 (in dem beide Komponenten Pulsare sind) sogar 16,90° pro Jahr.[36]
Die Lichtkurve des Quasars OJ 287 lässt vermuten, dass sich in seinem Zentrum zwei einander umkreisende Schwarze Löcher befinden, deren gegenseitiger Orbit sich pro 12-jährigem Umlauf um 39° dreht.[37]
Lange Zeit schien die Apsidendrehung des Doppelsternsystems DI Herculis im Widerspruch zu den physikalischen Gesetzen zu stehen, aber die geringe Geschwindigkeit der Apsidendrehung ist durch die Lage der Rotationsachse in der Bahnebene verursacht.[38]
Literatur
- (al-Battani 900): M. al-Battani: Zij. Ar-Raqqah, ca. 900; lat. Übersetzung: C.A. Nallino: Al-Battani sive Albatenii Opus Astronomicum. Mailand 1899–1907; Nachdruck Olms, Hildesheim 1977
- (Anderson 1987): J.D. Anderson, G. Colombo, P.B. Espsitio, E.L. Lau, G.B. Trager: The mass, gravity field, and ephemeris of Mercury. In: Icarus, 71, 1987, S. 337
- (Anderson 1991): J.D. Anderson, M.A. Slade, R.F. Jurgens, E.L. Lau, X.X. Newhall, E.M. Standish Jr.: Radar and Spacecraft Ranging to Mercury between 1966 and 1988. In: Proc. ASA, 9, 1991, S. 324
- (Anderson 1992): J.D. Anderson et al.: Recent Developments in Solar-System Tests of General Relativity. In: H. Sato, T. Nakamura (Hrsg.): Proc. Sixth Marcel Grossmann Meeting. World Scientific, Singapore (1992)
- (Burgay 2003): M. Burgay: An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. In: Nature, 426, 2003, S. 531–533, Abstract, arxiv:astro-ph/0312071
- (Dehnen 1988): H. Dehnen: Empirische Grundlagen und experimentelle Prüfung der Relativitätstheorie. In: J. Audretsch, K. Mainzer (Hrsg.): Philosophie und Physik der Raumzeit. Grundlagen der exakten Naturwissenschaften, Band 7. BI-Wissenschaftsverlag 1988
- (Einstein 1915): A. Einstein: Erklärung der Perihelbewegung des Merkur aus der Allgemeinen Relativitätstheorie. In: Sitzungsberichte der Preußischen Akademie der Wissenschaften, 1915, S. 831–839
- (Freundlich 1915): E. Freundlich: Über die Erklärung der Anomalien im Planeten-System durch die Gravitationswirkung interplanetarer Massen. In: Astronomische Nachrichten Nr. 4803, Bd. 201, 1915, S. 49–56, bibcode:1915AN....201...49F
- (Guthmann 2000): A. Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. 2. Auflage. Spektrum, Heidelberg 2000, ISBN 3-8274-0574-2
- (Hofmann-Wellenhof 1997): B. Hofmann-Wellenhof et al.: GPS – Theory and Practice. 4. Auflage. Springer, Wien 1997, ISBN 3-211-82839-7
- (Kramer 2006): M. Kramer et al.: Tests of general relativity from timing the double pulsar. In: Science Express, 14. Sept. 2006, arxiv:astro-ph/0609417
- (Lorimer 2006): D.R. Lorimer et al.: Arecibo Pulsar Survey Using ALFA. II. The Young, Highly Relativistic Binary Pulsar J1906+0746. In: ApJ, 640, 2006, S. 428–434 (Abstract)
- (Meeus 2000): J. Meeus: Astronomical Algorithms. 2nd ed., 2nd prnt., Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1
- (Morrison Ward 1975): L.V. Morrison, C.G. Ward: An Analysis of the Transits of Mercury: 1677–1973. In: Mon. Not. R. astr. Soc., 173, 1975, S. 183–206, bibcode:1975MNRAS.173..183M
- (Neugebauer 1975): O. Neugebauer: A History of Ancient Mathematical Astronomy. Springer, Berlin 1975, ISBN 3-540-06995-X
- (Nobili 1986): A. Nobili, C. Will: The real value of Mercury’s perihelion advance. In: Nature, 320, 1986, S. 39–41, bibcode:1986Natur.320...39N
- S. Oppenheim: Kritik des newtonschen Gravitationsgesetzes. In: Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. 6.2.2. Jahrgang, 1920, S. 80–158 (archive.org).
- (Pedersen 1974): O. Pedersen: A Survey of the Almagest. Odense University Press, 1974
- (Pijpers 1998): F.P. Pijpers: Helioseismic determination of the solar gravitational quadrupole moment. In: Mon. Not. R. Astron. Soc., 297, 1998, S. L76-L80, bibcode:1998MNRAS.297L..76P
- (Pitjeva 2005): E.V. Pitjeva: Relativistic Effects and Solar Oblateness from Radar Observations of Planets and Spacecraft. In: Astronomy Letters, 31, 2005, Band 5, S. 340–349, bibcode:2005AstL...31..340P
- (Ptolemäus 150): C. Ptolemäus: Almagest. Alexandria, ca. 150; dt. Übersetzung: Handbuch der Astronomie (übers. v. K. Manitius). Teubner, Leipzig 1963
- N. T Roseveare: Mercury’s perihelion from Leverrier to Einstein. University Press, Oxford 1982.
- (Saliba 1994): G. Saliba: A History of Arabic Astronomy. New York University Press, New York 1994, ISBN 0-8147-7962-X
- (Shapiro 1976) I.I. Shapiro, C.C. Counselman III, R.W. King: Verification of the principle of equivalence for massive bodies. In: Phys. Rev. Lett., 36, 1976, S. 555
- (Sivaram 1995): C. Sivaram: The Hulse-Taylor binary pulsar PSR1913+16. In: Bull. Astr. Soc. India, 23, 1995, S. 77–83, bibcode:1995BASI...23...77S
- (Will 1993): C.M. Will: Theory and Experiment in Gravitational Physics. Revised edition, Cambridge University Press, Cambridge 1993, ISBN 0-521-43973-6
- (Will 2006): C.M. Will: The Confrontation Between General Relativity and Experiment. In: Living Rev. Relativity, 9, 2006, arxiv:gr-qc/0510072
Weblinks
Einzelnachweise
- ↑ (Ptolemäus 150) Buch 3, Kap. 4
- ↑ (Pedersen 1974) S. 147
- ↑ (Ptolemäus 150) Buch 3, Kap. 4; Manitius Bd. I S. 167
- ↑ (Ptolemäus 150) Buch 3, Kap. 5; Manitius Bd. II S. 121
- ↑ (Neugebauer 1975) S. 58
- ↑ (al-Battani 900) S. 72 (Apogeum enim eodem motu quo sphaera stellarum fixarum volvitur, movetur, quem observationibus invenimus unius gradus esse in 66 annis Romanis […]", eigene Übersetzung)
- ↑ (al-Battani 900) S. 114 (Horum apogeorum [longitudines] motu sphaerae stellarum fixarum moventur, scilicet uno gradu in 66 annis solaribus […]", eigene Übersetzung).
- ↑ (Saliba 1994) S. 234
- ↑ (Neugebauer 1975) S. 480
- ↑ (Neugebauer 1975) S. 71
- ↑ (Will 1993), S. 181
- ↑ (Meeus 2000) Kap. 31
- ↑ vgl. zum Beispiel (Freundlich 1915)
- ↑ Oppenheim (1920), 153ff.
- ↑ Roseveare (1982), Kap. 6
- ↑ (Einstein 1915)
- ↑ 17,0 17,1 (Nobili 1986)
- ↑ (Guthmann 2000) S. 93ff
- ↑ (Will 2006) S. 38
- ↑ (Pitjeva 2005)
- ↑ (Morrison Ward 1975)
- ↑ (Shapiro 1976), zitiert nach (Pijpers 1998)
- ↑ (Anderson 1987), zitiert nach (Pijper 1998)
- ↑ (Anderson 1991)
- ↑ (Anderson 1992), zitiert nach (Pijper 1998)
- ↑ (Meeus 2000) Kap. 31, Zahlen gerundet
- ↑ Earth at Perihelion and Aphelion: 1501 to 1600 ... Earth at Perihelion and Aphelion: 2001 to 2100 ... Earth at Perihelion and Aphelion: 2401 to 2500 von Fred Espenak (astropixels.com), abgerufen am 8. Juli 2021
- ↑ (Neugebauer 1975) S. 1103ff
- ↑ Nautical Almanac. 1974, S. 107.; zit. nach Victor Reijs: Mean lunar and solar periods. In: The Moon and its path. 23. Februar 2001, abgerufen am 9. Mai 2010 (Lua-Fehler in Modul:Multilingual, Zeile 149: attempt to index field 'data' (a nil value)).
- ↑ Erste Forschungen von;; zitiert n. und weitere Literatur:;
- ↑ 31,0 31,1 (Hofmann-Wellenhof 1997) S. 62
- ↑ International Earth Rotation & Reference Systems Service: Useful Constants, aufgerufen am 15. August 2006
- ↑ (Nobili 1986), zitiert nach (Dehnen 1988)
- ↑ (Sivaram 1995), (Will 2006) Kap. 5
- ↑ (Lorimer 2006), (Will 2006) Kap. 5
- ↑ (Burgay 2003), (Will 2006) Kap. 5, (Kramer 2006)
- ↑ M.J. Valtonen et al.: Confirmation of the Gravitational Wave Energy Loss in the Binary Black Hole System OJ287. American Astronomical Society, AAS Meeting #211, #112.07 (2007), bibcode:2007AAS...21111207V
- ↑ S. Albrecht, S. Reffert, I. Snellen, J. Winn: Nature 461, 373-376 (2009)