Bifurkation (Mathematik): Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Nichtlineare Dynamik
- Theorie dynamischer Systeme
imported>Partynia (→Weblinks: +Wiktionary) |
imported>Krdbot K (Bot: Entferne 4 weiche Trennzeichen) |
||
| Zeile 1: | Zeile 1: | ||
Eine '''Bifurkation''' oder '''Verzweigung''' ist eine qualitative Zustandsänderung in [[Nichtlineare Systeme|nichtlinearen Systemen]] unter Einfluss eines Parameters <math>\mu</math>. Der Begriff der Bifurkation wurde von [[Henri Poincaré]] eingeführt. | Eine '''Bifurkation''' oder '''Verzweigung''' ist eine qualitative Zustandsänderung in [[Nichtlineare Systeme|nichtlinearen Systemen]] unter Einfluss eines Parameters <math>\mu</math><ref>{{Internetquelle |autor=Eric W. Weisstein |url=https://mathworld.wolfram.com/Bifurcation.html |titel=Bifurcation |sprache=en |abruf=2021-06-16}}</ref>. Der Begriff der Bifurkation wurde von [[Henri Poincaré]] eingeführt. | ||
Nichtlineare Systeme, deren Verhalten von einem Parameter abhängt, können bei einer Änderung des Parameters ihr Verhalten plötzlich ändern. Zum Beispiel kann ein System, das zuvor einem [[Grenzwert (Folge)|Grenzwert]] zustrebte, nun zwischen zwei Werten hin und her springen, also zwei [[Häufungspunkt]]e aufweisen. Dies nennt man eine '''Bifurkation'''. | Nichtlineare Systeme, deren Verhalten von einem Parameter abhängt, können bei einer Änderung des Parameters ihr Verhalten plötzlich ändern. Zum Beispiel kann ein System, das zuvor einem [[Grenzwert (Folge)|Grenzwert]] zustrebte, nun zwischen zwei Werten hin und her springen, also zwei [[Häufungspunkt]]e aufweisen. Dies nennt man eine '''Bifurkation'''. Bestimmte Systeme können unter finiter Änderung des Parameters <math>\mu</math> unendlich viele Bifurkationen erfahren und damit eine unendliche Menge an Häufungspunkten aufweisen. Das Verhalten solcher Systeme wandelt sich unter Änderung des Parameters <math>\mu</math> somit zu [[Deterministisches Chaos|deterministisch chaotischem Verhalten]]. Ein Beispiel hierfür ist die [[Logistische Gleichung|logistische Abbildung]]. | ||
Bestimmte Systeme können unter finiter Änderung des Parameters <math>\mu</math> unendlich viele Bifurkationen erfahren | |||
== Definition | == Definition == | ||
Ein dynamisches System kann durch eine Funktion <math>F(x)</math> beschrieben werden, die die zeitliche Entwicklung des Systemzustands <math>x</math> bestimmt. Diese Funktion sei nun von einem Parameter <math>\mu</math> abhängig, was man durch die Schreibweise <math>F(x,\mu)</math> ausdrückt. Wenn nun das System für Parameterwerte unterhalb eines bestimmten kritischen Werts <math>\mu_c</math> ein qualitativ anderes Verhalten aufweist als für Werte oberhalb von <math>\mu_c</math>, dann spricht man davon, dass das System bei <math>\mu_c</math> eine Bifurkation im Parameter <math>\mu</math> erfährt. Der Parameterwert <math>\mu_c</math> wird dann als Bifurkationspunkt bezeichnet. | Ein dynamisches System kann durch eine Funktion <math>F(x)</math> beschrieben werden, die die zeitliche Entwicklung des Systemzustands <math>x</math> bestimmt. Diese Funktion sei nun von einem Parameter <math>\mu</math> abhängig, was man durch die Schreibweise <math>F(x,\mu)</math> ausdrückt. Wenn nun das System für Parameterwerte unterhalb eines bestimmten kritischen Werts <math>\mu_c</math> ein qualitativ anderes Verhalten aufweist als für Werte oberhalb von <math>\mu_c</math>, dann spricht man davon, dass das System bei <math>\mu_c</math> eine Bifurkation im Parameter <math>\mu</math> erfährt. Der Parameterwert <math>\mu_c</math> wird dann als Bifurkationspunkt bezeichnet. | ||
| Zeile 12: | Zeile 11: | ||
== Bifurkationsdiagramm == | == Bifurkationsdiagramm == | ||
[[Datei: | [[Datei:LogisticMap BifurcationDiagram.png|miniatur|Abbildung 1: Bifurkationsdiagramm der [[logistische Gleichung|logistischen Gleichung]]]] Bifurkationen lassen sich in Bifurkationsdiagrammen graphisch darstellen. Bei einem eindimensionalen System werden dabei die Fixpunkte des Systems gegen den Parameter <math>\mu</math> aufgetragen. Für jeden Parameterwert wird so die Anzahl und die Lage dieser Punkte angezeigt. Zusätzlich kann man stabile und instabile Fixpunkte z. B. durch verschiedene Färbung unterscheiden. Bei einem System mit mehreren Variablen kann man ähnliche Diagramme zeichnen, indem man nur einen [[Unterraum]] des [[Phasenraum]]s betrachtet, etwa durch einen [[Poincaré-Schnitt]]. | ||
Das bekannteste Bifurkationsdiagramm ist das in Abbildung 1. gezeigte [[Feigenbaumdiagramm]], das sich aus der [[logistische Gleichung|logistischen Gleichung]] ableitet und eine Periodenverdoppelungsbifurkation abbildet. Man erkennt, dass bei kleinen Parameterwerten nur ein stabiler Fixpunkt existiert, der am ersten Bifurkationspunkt in einen Orbit aus zwei alternierenden | Das bekannteste Bifurkationsdiagramm ist das in Abbildung 1. gezeigte [[Feigenbaumdiagramm]], das sich aus der [[logistische Gleichung|logistischen Gleichung]] ableitet und eine Periodenverdoppelungsbifurkation abbildet. Man erkennt, dass bei kleinen Parameterwerten nur ein stabiler Fixpunkt existiert, der am ersten Bifurkationspunkt in einen Orbit aus zwei alternierenden [[Häufungspunkt]]en übergeht. Dieser Orbit verdoppelt dann an weiteren Bifurkationspunkten jedes Mal wieder seine Periode (kommt also erst nach 2, 4, 8 etc. Durchläufen wieder an den gleichen Punkt), bis er bei einem Parameterwert von etwa 3,57 in einen [[Chaostheorie|chaotischen]] Zustand übergeht, wo überhaupt keine Periode mehr erkennbar ist. All diese Übergänge lassen sich mithilfe des Bifurkationsdiagrammes gut veranschaulichen. | ||
Der [[Python (Programmiersprache)|Python]]-Code, um ein Bifurkationen-Diagramm für die [[logistische Gleichung]] zu erzeugen, lautet folgendermaßen:<syntaxhighlight lang="python3" line="1"> | |||
import numpy as np | |||
import matplotlib.pyplot as plt | |||
N_points = 4000000 | |||
N_steps = 500 | |||
r = np.linspace(0,4,N_points) | |||
#Initialwerte | |||
y = np.random.uniform(0,1,size=N_points) | |||
#Propagieren des Systems fuer lange Zeit um die Haeufungspunkte zu erreichen | |||
for _ in range(N_steps): | |||
y = r*y*(1-y) | |||
fig, biax = plt.subplots() | |||
biax.plot(r, y, '.-', linewidth=0, markersize=0.25) | |||
biax.set(xlabel='Wachstumsrate (r)', ylabel='Haeufungspunkte', title='Bifurcation') | |||
plt.show() | |||
</syntaxhighlight> | |||
== Beispiel == | == Beispiel == | ||
Ein typisches Beispiel einer Bifurkation ist das [[Knicken]] eines Stabes unter Druckbelastung. | Ein typisches Beispiel einer Bifurkation ist das [[Knicken]] eines Stabes unter Druckbelastung. | ||
Man stelle sich einen im Boden eingespannten, senkrecht stehenden, masselosen Stab mit | Man stelle sich einen im Boden eingespannten, senkrecht stehenden, masselosen Stab mit einer Last mit dem Gewicht <math>\mu</math> an der Spitze vor. Die Winkelabweichung des Stabes aus der Senkrechten entspricht dabei der Variablen x. | ||
Solange das Gewicht klein genug bleibt, ist <math>x = 0</math> eine stabile [[Gleichgewichtslage]] des Systems, d. h. für kleine Abweichungen richtet sich der Stab selbständig wieder in die Senkrechte | Solange das Gewicht klein genug bleibt, ist <math>x = 0</math> eine stabile [[Gleichgewichtslage]] des Systems, d. h. für kleine Abweichungen richtet sich der Stab selbständig wieder in die Senkrechte <math>(x = 0)</math> aus. | ||
Wird das Gewicht <math>\mu</math> kontinuierlich gesteigert, so wird bei einem bestimmten Gewicht (der Knicklast oder auch [[Knicken# | Wird das Gewicht <math>\mu</math> kontinuierlich gesteigert, so wird bei einem bestimmten Gewicht (der Knicklast oder auch [[Knicken#Mathematische Modelle des Knickproblems|Verzweigungslast]]) die senkrechte Gleichgewichtslage instabil. Gleichzeitig entstehen (für ein ebenes System) zwei neue (stabile) Gleichgewichtslagen (indem der Stab nach links oder rechts abknickt.) | ||
Der Übergang des Systems von einer (stabilen) zu drei (einer instabilen, zwei stabilen) Gleichgewichtslagen ist die Bifurkation, die in diesem Fall eine [[Pitchfork-Bifurkation]] ist. | Der Übergang des Systems von einer (stabilen) zu drei (einer instabilen, zwei stabilen) Gleichgewichtslagen ist die Bifurkation, die in diesem Fall eine [[Pitchfork-Bifurkation]] ist. | ||
== Typen | == Typen == | ||
* [[Pitchfork-Bifurkation]] | * [[Pitchfork-Bifurkation]] | ||
* [[Saddle-Node-Bifurkation]] | * [[Saddle-Node-Bifurkation]] | ||
| Zeile 35: | Zeile 55: | ||
* Hassan K. Khalil: ''Nonlinear Systems.'' 3. Auflage. Prentice Hall, 2002, ISBN 0-13-067389-7. | * Hassan K. Khalil: ''Nonlinear Systems.'' 3. Auflage. Prentice Hall, 2002, ISBN 0-13-067389-7. | ||
* R. I. Leine, H. Nijmeijer: ''Dynamics and Bifurcations in Non-Smooth Mechanical Systems.'' In: ''Lecture Notes in Applied and Computational Mechanics.'' Vol. 18, Springer-Verlag, Berlin/ Heidelberg/ New York 2004, ISBN 3-540-21987-0. | * R. I. Leine, H. Nijmeijer: ''Dynamics and Bifurcations in Non-Smooth Mechanical Systems.'' In: ''Lecture Notes in Applied and Computational Mechanics.'' Vol. 18, Springer-Verlag, Berlin/ Heidelberg/ New York 2004, ISBN 3-540-21987-0. | ||
* Steven H. Strogatz: ''Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering.'' Perseus Books Group, ISBN 0-7382-0453-6. | * [[Steven Strogatz|Steven H. Strogatz]]: ''Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering.'' Perseus Books Group, ISBN 0-7382-0453-6. | ||
*[[Martin Hermann (Mathematiker)|Martin Hermann]]: ''Numerik gewöhnlicher Differentialgleichungen.'' Band 2: Nichtlineare Randwertprobleme. Walter de Gruyter Verlag, Berlin und Boston 2018, ISBN 978-3-11-051488-9. | |||
== Weblinks == | == Weblinks == | ||
| Zeile 47: | Zeile 68: | ||
* [[Komplexes System]] | * [[Komplexes System]] | ||
* [[Mandelbrot-Menge]] | * [[Mandelbrot-Menge]] | ||
== Einzelnachweise == | |||
<references/> | |||
[[Kategorie:Nichtlineare Dynamik]] | [[Kategorie:Nichtlineare Dynamik]] | ||
[[Kategorie:Theorie dynamischer Systeme]] | [[Kategorie:Theorie dynamischer Systeme]] | ||
Aktuelle Version vom 23. Februar 2022, 03:16 Uhr
Eine Bifurkation oder Verzweigung ist eine qualitative Zustandsänderung in nichtlinearen Systemen unter Einfluss eines Parameters $ \mu $[1]. Der Begriff der Bifurkation wurde von Henri Poincaré eingeführt.
Nichtlineare Systeme, deren Verhalten von einem Parameter abhängt, können bei einer Änderung des Parameters ihr Verhalten plötzlich ändern. Zum Beispiel kann ein System, das zuvor einem Grenzwert zustrebte, nun zwischen zwei Werten hin und her springen, also zwei Häufungspunkte aufweisen. Dies nennt man eine Bifurkation. Bestimmte Systeme können unter finiter Änderung des Parameters $ \mu $ unendlich viele Bifurkationen erfahren und damit eine unendliche Menge an Häufungspunkten aufweisen. Das Verhalten solcher Systeme wandelt sich unter Änderung des Parameters $ \mu $ somit zu deterministisch chaotischem Verhalten. Ein Beispiel hierfür ist die logistische Abbildung.
Definition
Ein dynamisches System kann durch eine Funktion $ F(x) $ beschrieben werden, die die zeitliche Entwicklung des Systemzustands $ x $ bestimmt. Diese Funktion sei nun von einem Parameter $ \mu $ abhängig, was man durch die Schreibweise $ F(x,\mu ) $ ausdrückt. Wenn nun das System für Parameterwerte unterhalb eines bestimmten kritischen Werts $ \mu _{c} $ ein qualitativ anderes Verhalten aufweist als für Werte oberhalb von $ \mu _{c} $, dann spricht man davon, dass das System bei $ \mu _{c} $ eine Bifurkation im Parameter $ \mu $ erfährt. Der Parameterwert $ \mu _{c} $ wird dann als Bifurkationspunkt bezeichnet.
Was eine „qualitative Änderung“ ist, kann man formal mit dem Begriff der topologischen Äquivalenz bzw. der topologischen Konjugation beschreiben: Solange für zwei Parameterwerte $ \mu _{1} $ und $ \mu _{2} $ die Systeme $ F(x,\mu _{1}) $ und $ F(x,\mu _{2}) $ zueinander topologisch äquivalent sind, liegt keine qualitative Änderung im obigen Sinne vor.
Die Änderung am Bifurkationspunkt besteht in den meisten Fällen entweder in einer Änderung der Anzahl von Attraktoren wie Fixpunkte oder periodischen Orbits, oder eine Änderung der Stabilität dieser Objekte.
Bifurkationsdiagramm
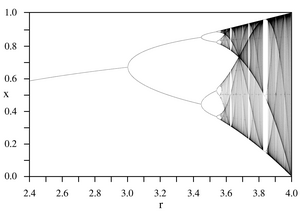
Bifurkationen lassen sich in Bifurkationsdiagrammen graphisch darstellen. Bei einem eindimensionalen System werden dabei die Fixpunkte des Systems gegen den Parameter $ \mu $ aufgetragen. Für jeden Parameterwert wird so die Anzahl und die Lage dieser Punkte angezeigt. Zusätzlich kann man stabile und instabile Fixpunkte z. B. durch verschiedene Färbung unterscheiden. Bei einem System mit mehreren Variablen kann man ähnliche Diagramme zeichnen, indem man nur einen Unterraum des Phasenraums betrachtet, etwa durch einen Poincaré-Schnitt.
Das bekannteste Bifurkationsdiagramm ist das in Abbildung 1. gezeigte Feigenbaumdiagramm, das sich aus der logistischen Gleichung ableitet und eine Periodenverdoppelungsbifurkation abbildet. Man erkennt, dass bei kleinen Parameterwerten nur ein stabiler Fixpunkt existiert, der am ersten Bifurkationspunkt in einen Orbit aus zwei alternierenden Häufungspunkten übergeht. Dieser Orbit verdoppelt dann an weiteren Bifurkationspunkten jedes Mal wieder seine Periode (kommt also erst nach 2, 4, 8 etc. Durchläufen wieder an den gleichen Punkt), bis er bei einem Parameterwert von etwa 3,57 in einen chaotischen Zustand übergeht, wo überhaupt keine Periode mehr erkennbar ist. All diese Übergänge lassen sich mithilfe des Bifurkationsdiagrammes gut veranschaulichen.
Der Python-Code, um ein Bifurkationen-Diagramm für die logistische Gleichung zu erzeugen, lautet folgendermaßen:<syntaxhighlight lang="python3" line="1"> import numpy as np import matplotlib.pyplot as plt
N_points = 4000000 N_steps = 500 r = np.linspace(0,4,N_points)
- Initialwerte
y = np.random.uniform(0,1,size=N_points)
- Propagieren des Systems fuer lange Zeit um die Haeufungspunkte zu erreichen
for _ in range(N_steps):
y = r*y*(1-y)
fig, biax = plt.subplots() biax.plot(r, y, '.-', linewidth=0, markersize=0.25) biax.set(xlabel='Wachstumsrate (r)', ylabel='Haeufungspunkte', title='Bifurcation') plt.show() </syntaxhighlight>
Beispiel
Ein typisches Beispiel einer Bifurkation ist das Knicken eines Stabes unter Druckbelastung.
Man stelle sich einen im Boden eingespannten, senkrecht stehenden, masselosen Stab mit einer Last mit dem Gewicht $ \mu $ an der Spitze vor. Die Winkelabweichung des Stabes aus der Senkrechten entspricht dabei der Variablen x.
Solange das Gewicht klein genug bleibt, ist $ x=0 $ eine stabile Gleichgewichtslage des Systems, d. h. für kleine Abweichungen richtet sich der Stab selbständig wieder in die Senkrechte $ (x=0) $ aus. Wird das Gewicht $ \mu $ kontinuierlich gesteigert, so wird bei einem bestimmten Gewicht (der Knicklast oder auch Verzweigungslast) die senkrechte Gleichgewichtslage instabil. Gleichzeitig entstehen (für ein ebenes System) zwei neue (stabile) Gleichgewichtslagen (indem der Stab nach links oder rechts abknickt.) Der Übergang des Systems von einer (stabilen) zu drei (einer instabilen, zwei stabilen) Gleichgewichtslagen ist die Bifurkation, die in diesem Fall eine Pitchfork-Bifurkation ist.
Typen
- Pitchfork-Bifurkation
- Saddle-Node-Bifurkation
- Hopf-Bifurkation
- Transkritische Bifurkation
- Flip-Bifurkation
Literatur und Quellen
- Hassan K. Khalil: Nonlinear Systems. 3. Auflage. Prentice Hall, 2002, ISBN 0-13-067389-7.
- R. I. Leine, H. Nijmeijer: Dynamics and Bifurcations in Non-Smooth Mechanical Systems. In: Lecture Notes in Applied and Computational Mechanics. Vol. 18, Springer-Verlag, Berlin/ Heidelberg/ New York 2004, ISBN 3-540-21987-0.
- Steven H. Strogatz: Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering. Perseus Books Group, ISBN 0-7382-0453-6.
- Martin Hermann: Numerik gewöhnlicher Differentialgleichungen. Band 2: Nichtlineare Randwertprobleme. Walter de Gruyter Verlag, Berlin und Boston 2018, ISBN 978-3-11-051488-9.
Weblinks
- World of Bifurcation (englisch)
- Bifurcations and Two Dimensional Flows by Elmer G. Wiens (englisch)
Siehe auch
- Nichtlineare Dynamik
- Fraktale Geometrie
- Komplexes System
- Mandelbrot-Menge
Einzelnachweise
- ↑ Eric W. Weisstein: Bifurcation. Abgerufen am 16. Juni 2021 (Lua-Fehler in Modul:Multilingual, Zeile 149: attempt to index field 'data' (a nil value)).