Newtonsches Gravitationsgesetz: Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Gravitation
- Isaac Newton als Namensgeber
imported>Regi51 K (Änderungen von 85.216.123.104 (Diskussion) rückgängig gemacht (HG) (3.3.2)) |
imported>Wassermaus |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:NewtonsLawOfUniversalGravitation.svg|miniatur|Die äquivalenten Anziehungskräfte zweier Massen]] | [[Datei:NewtonsLawOfUniversalGravitation.svg|miniatur|Die äquivalenten Anziehungskräfte zweier Massen]] | ||
Das ''' | Das '''Newtonsche Gravitationsgesetz''' ist ein [[physikalisches Gesetz|Gesetz]] der [[Klassische Physik|klassischen Physik]], nach dem jeder [[Massenpunkt]] auf jeden anderen Massenpunkt mit einer anziehenden [[Gravitation]]skraft einwirkt. Diese Gravitationskraft ist entlang der Verbindungslinie beider Massenpunkte gerichtet sowie in ihrer Stärke proportional zum Produkt der beiden Massen und umgekehrt proportional zum Quadrat ihres Abstandes. Bei ausgedehnten Körpern gilt dieses Gesetz für jeden Massenpunkt des einen Körpers in Beziehung zu jedem Massenpunkt des anderen Körpers, die einzelnen Kräfte [[Parallelogramm der Kräfte|summieren ]] sich zu einer Gesamtkraft. | ||
Das | Das Newtonsche Gravitationsgesetz ist eines der grundlegenden Gesetze der klassischen Physik. Es wurde von [[Isaac Newton]] in seinem 1687 erschienenen Werk ''[[Philosophiae Naturalis Principia Mathematica]]'' aufgestellt. Damit gelang Newton im Rahmen der von ihm zugleich begründeten [[Klassische Mechanik|klassischen Mechanik]] die erste gemeinsame Erklärung für die [[Schwerkraft]] auf der Erde, für den Mondumlauf um die Erde und für die [[Planetenbewegung]] um die Sonne. Die Newtonsche Gravitationstheorie erklärt diese und weitere mit der Gravitation zusammenhängenden Phänomene wie die [[Gezeiten]] auf der Erde und [[Bahnstörung]]en des Mondes und der Planeten mit großer Genauigkeit. Verbleibende Unstimmigkeiten wurden erst Anfang des 20. Jahrhunderts durch die von [[Albert Einstein]] entwickelte [[allgemeine Relativitätstheorie]] geklärt. | ||
== Geschichte == | == Geschichte == | ||
Eine erste intensivere Beschäftigung Newtons mit der physikalischen Beschreibung der Planetenbahnen und der Rolle der Schwerkraft, die in seinem [[annus mirabilis]] 1665/66 erfolgte, enthielt teilweise das Konzept einer quadratisch abnehmenden Schwerkraft. Newton begründete das aber nicht bzw. ging von falschen Annahmen aus, insbesondere noch nicht vom Gedanken der universellen (also außerirdischen) Wirkung der Schwerkraft.<ref>[https://dgg-online.de/WordPress_01/wp-content/uploads/2016/10/160127_DGG_1_16_web.pdf | [[Datei:Mplwp 1overxsquared positive.svg|mini|Abnahme der Gravitationskraft mit dem Quadrat der Entfernung: 1/x<sup>2</sup>]] | ||
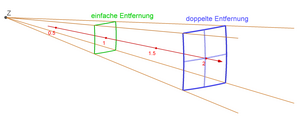
[[Datei:Quadratischer_Abfall,_Veranschaulichung nach_Martin_Wagenschein_(GeoGebra).png|mini|Veranschaulichung der quadratischen Abnahme der Gravitation mit der Entfernung nach [[Martin Wagenschein]] ([[Der Mond und seine Bewegung]])]] | |||
Eine erste intensivere Beschäftigung Newtons mit der physikalischen Beschreibung der Planetenbahnen und der Rolle der Schwerkraft, die in seinem [[annus mirabilis]] 1665/66 erfolgte, enthielt teilweise das Konzept einer quadratisch abnehmenden Schwerkraft. Newton begründete das aber nicht bzw. ging von falschen Annahmen aus, insbesondere noch nicht vom Gedanken der universellen (also außerirdischen) Wirkung der Schwerkraft.<ref>Jürgen Fertig: ''[https://dgg-online.de/WordPress_01/wp-content/uploads/2016/10/160127_DGG_1_16_web.pdf Isaac Newtons erster Mondtest, der keiner war!]'' (PDF; 4,5 MB). In: ''Mitteilungen der Deutschen Geophysikalischen Gesellschaft e.V.'' 1/2016.</ref> | |||
Vom Jahr 1678 an beschäftigte Newton sich, in Zusammenarbeit mit [[Robert Hooke|Hooke]] und [[John Flamsteed|Flamsteed]], intensiv mit Mechanik, insbesondere mit den keplerschen Gesetzen. In einem Briefwechsel mit Newton erwähnte Hooke seine Theorie der Planetenbewegung, darin war die Rede von einer Anziehungskraft, die mit der Entfernung abnimmt; in Newtons Antwort ging dieser von konstanter Schwerkraft aus. Dieser Briefwechsel war Ausgangspunkt des späteren [[Plagiat]]svorwurfs von Hooke an Newton. Newton räumte dabei ein, dass Hooke ihn auf den richtigen Weg geführt habe: | Vom Jahr 1678 an beschäftigte Newton sich, in Zusammenarbeit mit [[Robert Hooke|Hooke]] und [[John Flamsteed|Flamsteed]], intensiv mit Mechanik, insbesondere mit den keplerschen Gesetzen. In einem Briefwechsel mit Newton erwähnte Hooke seine Theorie der Planetenbewegung, darin war die Rede von einer Anziehungskraft, die mit der Entfernung abnimmt; in Newtons Antwort ging dieser von konstanter Schwerkraft aus. Dieser Briefwechsel war Ausgangspunkt des späteren [[Plagiat]]svorwurfs von Hooke an Newton. Newton räumte dabei ein, dass Hooke ihn auf den richtigen Weg geführt habe: Sowohl die Idee, dass die Bahnellipse von einer (mit dem Quadrat der Entfernung von einem Brennpunkt) abnehmenden Anziehungskraft herrührt, stamme von Hooke wie auch der Gedanke, dass dieses Konzept auch für planetarische Bewegungen anwendbar ist. Hookes Vorschlag abnehmender Schwerkraft beruhte allerdings auf [[Intuition]] und nicht – wie bei Newton – auf Beobachtung und logischer Ableitung. | ||
Seine vorläufigen Ergebnisse veröffentlichte Newton 1684 unter dem Titel ''De Motu Corporum'' | Seine vorläufigen Ergebnisse veröffentlichte Newton 1684 unter dem Titel ''De Motu Corporum.'' Darauf aufbauend legte er 1687 in seinem dreibändigen Werk ''[[Philosophiae Naturalis Principia Mathematica]] (Mathematische Grundlagen der Naturphilosophie)'' die Grundsteine der [[Klassische Mechanik|klassischen Mechanik]]. Darin formulierte Newton die drei [[Newtonsche Gesetze|Newtonschen Gesetze]] der Bewegung und das Gravitationsgesetz, Letzteres allerdings nicht in der knappen Form wie am Anfang dieses Artikels wiedergegeben, sondern über mehrere Abschnitte verteilt. Er begründete die Gesetze ausführlich unter erstmaliger Verwendung der von ihm geschaffenen geometrischen Form der [[Infinitesimalrechnung]]. Der dritte Teil des Werkes beschäftigt sich unter dem Titel ''Über das Weltsystem'' mit der Anwendung der neuen Gesetze auf die tatsächlichen Bewegungen von Himmelskörpern, wobei Newton seine Berechnungen mit einer Vielzahl von Messdaten anderer Naturforscher vergleicht und auf diese Weise die Richtigkeit seiner theoretischen Herleitungen belegt. | ||
[[Henry Cavendish]] gelang es 1797 als | [[Henry Cavendish]] gelang es 1797 als Erstem, in einem Experiment mit einer empfindlichen [[Drehwaage]] die gegenseitige Anziehung zweier Körper bekannter Masse experimentell zu messen,<ref>Henry Cavendish: ''[[:Datei:Cavendish-Experiments to Determine the Density of the Earth..pdf|Experiments to determine the Density of the Earth.]]'' (PDF) 1798 (englisch).</ref> wie es aus dem Newtonschen Gravitationsgesetz folgt. Der Messapparat ist ähnlich der Torsionswaage, mit der [[Charles Augustin de Coulomb]] 1785 die elektrostatische Anziehung und Abstoßung untersucht hatte, sie stammt ursprünglich von dem Geologen [[John Michell]]. Für den Nachweis der Gravitation musste Cavendish den Einfluss kleinster Störungen ausschließen, beispielsweise bediente er deshalb sein Experiment aus einem anderen Raum und machte die Ablesungen mit einem Fernrohr. | ||
In der heute gebräuchlichen expliziten Form wurde das Gravitationsgesetz nicht von Newton selbst, sondern erst 1873, also 200 Jahre später, von [[Alfred Cornu]] und [[Jean-Baptistin Baille]] formuliert.<ref name="SpeakeQuinn2014">{{Literatur|Autor=Clive Speake, Terry Quinn|Titel=The search for Newton’s constant|Sammelwerk=Physics Today|Band=Bd. 67|Nummer=7| | In der heute gebräuchlichen expliziten Form wurde das Gravitationsgesetz nicht von Newton selbst, sondern erst 1873, also 200 Jahre später, von [[Alfred Cornu]] und [[Jean-Baptistin Baille]] formuliert.<ref name="SpeakeQuinn2014">{{Literatur |Autor=Clive Speake, Terry Quinn |Titel=The search for Newton’s constant |Sammelwerk=Physics Today |Band=Bd. 67 |Nummer=7 |Datum=2014 |Seiten=27 |DOI=10.1063/PT.3.2447}}</ref><ref>{{Literatur |Autor=A. Cornu, J. Baille |Titel=Détermination nouvelle de la constante de l’attraction et de la densité moyennede la Terre |Sammelwerk=Comptes Rendus Hebd. Seances Acad. Sci. |Band=76 |Datum=1873 |Seiten=954 |Online=[https://gallica.bnf.fr/ark:/12148/bpt6k3033b/f954.image online] |Abruf=2019-04-03}}</ref> | ||
Bis dahin hatte man das Newtonsche Gravitationsgesetz lediglich in seiner ursprünglichen Form verwendet, d. h. in Gestalt der Proportionalitäten <math>F \propto m_1\ ,\ F \propto m_2\ ,\ F \propto r^{-2}</math>, und ohne Definition einer „Gravitationskonstanten“. | |||
Das Newtonsche Gravitationsgesetz ermöglichte eine wesentlich genauere Berechnung der Positionen der Planeten als früher. Die nach [[Ptolomäus]] oder [[Kopernikus]] berechneten Positionen wichen oftmals um <math>10^{\prime}</math> (das entspricht 1/3 Monddurchmesser) von den Beobachtungen ab, die nach den [[Keplersche Gesetze|keplerschen Gesetzen]] berechneten noch um bis zu <math>1^{\prime}</math>.<ref>{{Literatur | Das Newtonsche Gravitationsgesetz ermöglichte eine wesentlich genauere Berechnung der Positionen der Planeten als früher. Die nach [[Ptolomäus]] oder [[Kopernikus]] berechneten Positionen wichen oftmals um <math>10^{\prime}</math> (das entspricht 1/3 Monddurchmesser) von den Beobachtungen ab, die nach den [[Keplersche Gesetze|keplerschen Gesetzen]] berechneten noch um bis zu <math>1^{\prime}</math>.<ref>{{Literatur |Autor=Gearhart, C.A. |Titel=Epicycles, eccentrics, and ellipses: The predictive capabilities of Copernican planetary models |Sammelwerk=Archive for History of Exact Sciences |Band=Bd. 32 |Nummer=3 |Datum=1985 |DOI=10.1007/BF00348449 |Seiten=207–222}}</ref> Dagegen gelang es mithilfe der Newtonschen [[Himmelsmechanik]], diese als [[Bahnstörung]]en bezeichneten Abweichungen auf die Anziehung durch die anderen Planeten zurückzuführen. Im Fall des [[Uranus (Planet)|Uranus]] wurde daraus sogar auf die Existenz eines bis dahin unbekannten Planeten, des [[Neptun (Planet)|Neptun]], geschlossen, dessen ungefähre Position erstmals von [[Urbain Le Verrier]] aus den genauen Werten der Bahnstörung berechnet wurde<ref>James Lequeux: ''Le Verrier — Magnificent and Detestable Astronomer.'' Springer Verlag, 2013. S. 23.</ref>. Kurz danach entdeckte [[Johann Gottfried Galle]] den neuen Planeten in einer Entfernung von nur einem Bogengrad von der Vorhersage.<ref>Thomas Bührke: ''Sternstunden der Astronomie. Von Kopernikus bis Oppenheimer.'' München 2001, S. 150.</ref> Jedoch ließ sich die später entdeckte [[Periheldrehung]] der Bahn des [[Merkur (Planet)|Merkur]] mit der gleichen Methode nur zu etwa 90 % erklären. Für die volle Erklärung musste erst die [[allgemeine Relativitätstheorie]] entwickelt werden. Diese weitaus umfassendere Theorie enthält das Newtonsche Gravitationsgesetz als denjenigen Grenzfall, der nur für hinreichend kleine Massendichten und Geschwindigkeiten gilt. | ||
|Autor=Gearhart, C.A. |Titel=Epicycles, eccentrics, and ellipses: The predictive capabilities of Copernican planetary models |Sammelwerk=Archive for History of Exact Sciences |Band=Bd. 32 |Nummer=3 | | |||
Dagegen gelang es mithilfe der | |||
== Mathematische Formulierung == | == Mathematische Formulierung == | ||
| Zeile 25: | Zeile 26: | ||
:<math>F = G \frac{m_1 m_2}{r^2}</math> | :<math>F = G \frac{m_1 m_2}{r^2}</math> | ||
Die Größe <math>G</math> ist die [[Gravitationskonstante]]. Die auf die beiden Massen wirkenden Kräfte | Die Größe <math>G</math> ist die [[Gravitationskonstante]]. Die auf die beiden Massen wirkenden Kräfte haben denselben [[Betrag eines Vektors|Betrag]] und zeigen jeweils auf den anderen Massepunkt (siehe Abbildung). Das Newtonsche Gravitationsgesetz beschreibt damit im Gegensatz zum mathematisch ähnlichen [[Coulombsches Gesetz|coulombschen Gesetz]] eine immer anziehende Kraft. | ||
==== Vektoriell ==== | |||
In vektorieller Form gilt für die auf Massepunkt 1 wirkende Kraft <math>\vec{F}_1</math> | |||
:<math>\vec{F}_1 = G \frac{m_1 m_2}{r^3} \vec r_{12} = G \frac{m_1 m_2}{|\vec r_2 - \vec r_1|^3} (\vec r_2 - \vec r_1)</math>, | |||
wobei <math>\vec {r}_1</math> und <math>\vec {r}_2</math> die Positionen ([[Ortsvektor]]en) der beiden Massepunkte sind.<ref>{{Literatur |Autor=Walter Greiner |Titel=Klassische Mechanik 1. Kinematik und Dynamik der Punktteilchen. Relativität |Auflage=8., überarb. u. erw. Aufl |Verlag=Harri Deutsch |Ort=Frankfurt |Datum=2008 |ISBN=9783817118151 |Seiten=4}}</ref> | |||
Daraus resultiert nach dem [[Newtonsche Axiome#Zweites | <math>\vec F_2</math> zeigt auf Massepunkt 1 und ist der [[Gegenvektor]] zu <math>\vec F_1</math>:<blockquote><math>\vec F_2 = -\vec F_1</math>.</blockquote>Wird der Massepunkt 1 von mehreren Massepunkten 2, 3, … , n angezogen, so addieren sich die einzelnen Kräfte zur auf Massepunkt 1 wirkenden Gesamtkraft | ||
:<math>a_1 = \frac{F_1}{m_1} </math>, | |||
:<math>\vec{F}_1 = Gm_1 \sum_{i=2}^n m_i \frac{\vec{r}_i-\vec{r}_1}{|\vec{r}_i-\vec{r}_1|^3}</math> | |||
==== Gravitationsbeschleunigung ==== | |||
Daraus resultiert nach dem [[Newtonsche Axiome#Zweites Newtonsches Gesetz|zweiten Newtonschen Axiom]] eine Beschleunigung mit dem Betrag | |||
:<math>a_1 = \frac{F_1}{m_1}</math>, | |||
die auch ''Gravitationsbeschleunigung'' oder ''Gravitationsfeldstärke'' am Ort der Masse <math>m_1</math> genannt wird (siehe [[Gravitationsfeld]]). | die auch ''Gravitationsbeschleunigung'' oder ''Gravitationsfeldstärke'' am Ort der Masse <math>m_1</math> genannt wird (siehe [[Gravitationsfeld]]). | ||
Zwei Punktmassen <math>m_1</math> und <math>m_2</math> erfahren im Abstand <math>r</math> bei Abwesenheit anderer Kräfte durch das | Zwei Punktmassen <math>m_1</math> und <math>m_2</math> erfahren im Abstand <math>r</math> bei Abwesenheit anderer Kräfte durch das Newtonsche Gravitationsgesetz die Beschleunigungen: | ||
:<math>a_1 = \frac{F}{m_1} = G \frac{m_2}{r^2} \qquad \text{bzw.} \qquad a_2 = \frac{F}{m_2} = G \frac{m_1}{r^2}</math> | :<math>a_1 = \frac{F}{m_1} = G \frac{m_2}{r^2} \qquad \text{bzw.} \qquad a_2 = \frac{F}{m_2} = G \frac{m_1}{r^2}</math> | ||
Die Masse <math>m_1</math> zieht die Masse <math>m_2</math> an und umgekehrt. Beide Massen werden zum gemeinsamen [[Massenmittelpunkt|Schwerpunkt]] hin beschleunigt. Von einem der Körper aus gesehen bewegt sich der andere mit einer Beschleunigung, die die Summe der Einzelbeschleunigungen ist: | Die Masse <math>m_1</math> zieht die Masse <math>m_2</math> an und umgekehrt. Beide Massen werden zum gemeinsamen [[Massenmittelpunkt|Schwerpunkt]] hin beschleunigt. Von einem der Körper aus gesehen bewegt sich der andere mit einer Beschleunigung, die die Summe der Einzelbeschleunigungen ist: | ||
:<math>a_1 + a_2 = G\, \frac{m_1+m_2}{r^2}</math> | :<math>a_1 + a_2 = G\, \frac{m_1+m_2}{r^2}</math> | ||
Falls nun eine der Massen viel kleiner ist als die andere, reicht es näherungsweise aus, nur die größere Masse zu berücksichtigen. So hat die Erde viel mehr Masse als ein Apfel, ein Mensch oder ein LKW, | Falls nun eine der Massen viel kleiner ist als die andere, reicht es näherungsweise aus, nur die größere Masse zu berücksichtigen. So hat die Erde viel mehr Masse als ein Apfel, ein Mensch oder ein LKW, sodass es für alle diese Objekte reicht, die Masse der Erde in die Gleichung für die Beschleunigung einzusetzen. Alle drei Objekte werden, wenn sie sich an demselben Ort befinden, gleich stark in Richtung Erdmitte beschleunigt. Sie fallen gleich schnell und in dieselbe Richtung. Wenn man jedoch ein [[Doppelstern]]system betrachtet, muss man beide Sternmassen berücksichtigen, weil sie etwa gleich groß sind. | ||
Wenn sich <math>r</math> während der Bewegung eines Objektes nur sehr geringfügig verändert, ist die Gravitationsbeschleunigung praktisch konstant, etwa bei einem Gegenstand nahe der Erdoberfläche, der nur einige Meter tief fällt, also verschwindend wenig im Vergleich zum Erdradius von ''r'' = ca. 6370 km. In einem hinreichend kleinen Bereich kann also das Gravitationsfeld als homogen betrachtet werden. Wenn man die Veränderung der Gravitationskraft mit dem Abstand nicht vernachlässigen kann, ist eine Berechnung beispielsweise der Auftreffgeschwindigkeit eines frei fallenden Körpers mithilfe der Integralrechnung möglich, d. h. über das [[Gravitationsfeld#Potential und Feld|Gravitationspotential]] | Wenn sich <math>r</math> während der Bewegung eines Objektes nur sehr geringfügig verändert, ist die Gravitationsbeschleunigung praktisch konstant, etwa bei einem Gegenstand nahe der Erdoberfläche, der nur einige Meter tief fällt, also verschwindend wenig im Vergleich zum Erdradius von {{nowrap|1=''r'' = ca. 6370 km.}} In einem hinreichend kleinen Bereich kann also das Gravitationsfeld als homogen betrachtet werden. Wenn man die Veränderung der Gravitationskraft mit dem Abstand nicht vernachlässigen kann, ist eine Berechnung beispielsweise der Auftreffgeschwindigkeit eines frei fallenden Körpers mithilfe der Integralrechnung möglich, d. h. über das [[Gravitationsfeld#Potential und Feld|Gravitationspotential]] | ||
:<math>\Phi(r)=-\frac{Gm}{r}</math>. | :<math>\Phi(r)=-\frac{Gm}{r}</math>. | ||
| Zeile 53: | Zeile 60: | ||
Reale Körper sind keine Punktmassen, sondern haben eine räumliche Ausdehnung. Da das Gravitationsgesetz linear in den Massen ist, kann der Körper gedanklich in kleine Teile zerlegt werden, deren Beiträge, wie im vorigen Abschnitt gezeigt, vektoriell addiert werden können. Beim Grenzübergang zu unendlich kleinen Teilen ergibt sich statt einer Summe ein [[Integralrechnung|Integral]]. | Reale Körper sind keine Punktmassen, sondern haben eine räumliche Ausdehnung. Da das Gravitationsgesetz linear in den Massen ist, kann der Körper gedanklich in kleine Teile zerlegt werden, deren Beiträge, wie im vorigen Abschnitt gezeigt, vektoriell addiert werden können. Beim Grenzübergang zu unendlich kleinen Teilen ergibt sich statt einer Summe ein [[Integralrechnung|Integral]]. | ||
Auf diese Weise kann unter anderem gezeigt werden, dass ein Objekt mit sphärisch symmetrischer Massenverteilung im Außenraum dieselbe Gravitationswirkung hat, als wäre seine gesamte Masse in seinem Schwerpunkt vereinigt. Daher können ausgedehnte Himmelskörper näherungsweise als Massenpunkte behandelt werden. Im ''Innern'' einer [[Ellipse|elliptischen]] oder kugelsymmetrischen homogenen Massenverteilung, z. B. einer [[Hohlkugel]], ist die Gravitationskraft null. Daraus folgt, dass in einem beliebigen Abstand <math>r</math> vom Mittelpunkt einer kugelsymmetrischen Massenverteilung die Gravitationskraft genau von dem Anteil der Gesamtmasse erzeugt wird, der innerhalb einer Kugel mit dem Radius <math>r</math> liegt. Newton hat dieses Theorem (das auch als ''' | Auf diese Weise kann unter anderem gezeigt werden, dass ein Objekt mit sphärisch symmetrischer Massenverteilung im Außenraum dieselbe Gravitationswirkung hat, als wäre seine gesamte Masse in seinem Schwerpunkt vereinigt. Daher können ausgedehnte Himmelskörper näherungsweise als Massenpunkte behandelt werden. Im ''Innern'' einer [[Ellipse|elliptischen]] oder kugelsymmetrischen homogenen Massenverteilung, z. B. einer [[Hohlkugel]], ist die von dieser Masse ausgehende Gravitationskraft null. Daraus folgt, dass in einem beliebigen Abstand <math>r</math> vom Mittelpunkt einer kugelsymmetrischen Massenverteilung die Gravitationskraft genau von dem Anteil der Gesamtmasse erzeugt wird, der innerhalb einer Kugel mit dem Radius <math>r</math> liegt. Newton hat dieses Theorem (das auch als '''[[Newtonsches Schalentheorem]]''' bezeichnet wird) in seiner ''[[Philosophiae Naturalis Principia Mathematica]]'' bewiesen. Für nicht elliptisch symmetrische Körper oder inhomogene Massenverteilungen gilt das Theorem im Allgemeinen nicht. Ebenso ist zu beachten, dass die Gravitation keine Gegenkraft besitzt, also nicht abgeschirmt werden kann. Das tatsächliche Gravitationsfeld in einer Hohlkugel wäre somit nicht null, da im Inneren natürlich die Gravitationskräfte aller anderen im Universum vorhandenen Massen wirken würden – nur die Kugelschale selbst würde nichts beitragen. | ||
== Grenzen der Theorie == | == Grenzen der Theorie == | ||
Obwohl es für praktische Zwecke hinreichend genau ist, ist das | Obwohl es für praktische Zwecke hinreichend genau ist, ist das Newtonsche Gravitationsgesetz nur eine Näherung für schwache und zeitunabhängige Gravitationsfelder. Für starke Felder verwendet man die genauere Beschreibung mittels der [[Allgemeine Relativitätstheorie|allgemeinen Relativitätstheorie]], aus der die [[Poisson-Gleichung]] der klassischen Gravitationstheorie und damit auch das Newtonsche Gravitationsgesetz direkt hergeleitet werden kann, wenn man nur annimmt, dass es sich bei der Gravitation um ein [[Konservative Kraft|konservatives Feld]] handelt. Man bezeichnet das Gesetz daher heute oft als ''Grenzfall kleiner Felder.'' Die allgemeine Relativitätstheorie löst insbesondere auch die hier beschriebenen Probleme der Newtonschen Gravitationstheorie. | ||
=== Theoretische Grenzen === | === Theoretische Grenzen === | ||
* Die | * Die Newtonsche Theorie ist eine ''effektive Theorie,'' das bedeutet, sie gibt weder eine Ursache für die Gravitationskraft an, noch erklärt sie, wie die Gravitation über die Entfernung wirken kann. Viele Zeitgenossen, darunter Newton selbst und auch noch [[Leonhard Euler]], lehnten die Möglichkeit einer unmittelbaren [[Nahwirkung und Fernwirkung|Fernwirkung]] durch den leeren Raum ab. Um diese Erklärungslücke zu schließen, wurde die sogenannte [[Le-Sage-Gravitation]] als Modell entwickelt, das sich jedoch nie wirklich durchsetzen konnte. | ||
* Die | * Die Newtonsche Theorie setzt voraus, dass sich die Gravitationswirkung unendlich schnell ausbreitet, damit die keplerschen Gesetze erfüllt sind. Dies führt zu Konflikten mit der [[Spezielle Relativitätstheorie|speziellen Relativitätstheorie]]. Diese fordert nämlich, dass sich auch die Gravitation nur mit Lichtgeschwindigkeit ausbreitet. | ||
* Die [[Äquivalenzprinzip (Physik)|Äquivalenz von träger und schwerer Masse]] ist in der | * Die [[Äquivalenzprinzip (Physik)|Äquivalenz von träger und schwerer Masse]] ist in der Newtonschen Mechanik nicht erklärt. | ||
=== Widersprüche zur Beobachtung === | === Widersprüche zur Beobachtung === | ||
* Die | * Die Newtonsche Theorie erklärt nicht vollständig die [[Apsidendrehung|Periheldrehung]] der Planetenumlaufbahnen, besonders des [[Merkur (Planet)|Merkur]]. Bei diesem beträgt der Unterschied zwischen der nach der Newtonschen Theorie berechneten und der beobachteten Periheldrehung 43 [[Bogensekunde]]n pro Jahrhundert. | ||
* Ob Licht im Gravitationsfeld abgelenkt wird oder nicht, hängt in der | * Ob Licht im Gravitationsfeld abgelenkt wird oder nicht, hängt in der Newtonschen Theorie davon ab, welche Natur dem Licht zugeschrieben wird. Wird es als [[elektromagnetische Welle]] aufgefasst, dann ergibt sich keine Ablenkung. Wird es jedoch gemäß der [[Korpuskeltheorie]] als massebehaftetes Teilchen aufgefasst, dann ergibt sich gemäß dem Newtonschen Gravitationsgesetz eine [[Lichtablenkung]], wobei aus der Bewegungsgleichung eine Vorhersage gemacht werden kann, die unabhängig von der Masse ist und somit auch im Grenzfall verschwindender Masse gültig bleibt. Dieser Wert beträgt jedoch nur die Hälfte der tatsächlich beobachteten Ablenkung. | ||
Für beide Effekte ergibt sich der gemessene Wert korrekt aus den Gleichungen der allgemeinen Relativitätstheorie. | |||
== Literatur == | == Literatur == | ||
| Zeile 73: | Zeile 82: | ||
| ISBN = 9783540260349 | | ISBN = 9783540260349 | ||
| Verlag = Springer | | Verlag = Springer | ||
| | | Datum = 2006}} | ||
== Einzelnachweise == | == Einzelnachweise == | ||
Aktuelle Version vom 6. Januar 2022, 11:37 Uhr
Das Newtonsche Gravitationsgesetz ist ein Gesetz der klassischen Physik, nach dem jeder Massenpunkt auf jeden anderen Massenpunkt mit einer anziehenden Gravitationskraft einwirkt. Diese Gravitationskraft ist entlang der Verbindungslinie beider Massenpunkte gerichtet sowie in ihrer Stärke proportional zum Produkt der beiden Massen und umgekehrt proportional zum Quadrat ihres Abstandes. Bei ausgedehnten Körpern gilt dieses Gesetz für jeden Massenpunkt des einen Körpers in Beziehung zu jedem Massenpunkt des anderen Körpers, die einzelnen Kräfte summieren sich zu einer Gesamtkraft.
Das Newtonsche Gravitationsgesetz ist eines der grundlegenden Gesetze der klassischen Physik. Es wurde von Isaac Newton in seinem 1687 erschienenen Werk Philosophiae Naturalis Principia Mathematica aufgestellt. Damit gelang Newton im Rahmen der von ihm zugleich begründeten klassischen Mechanik die erste gemeinsame Erklärung für die Schwerkraft auf der Erde, für den Mondumlauf um die Erde und für die Planetenbewegung um die Sonne. Die Newtonsche Gravitationstheorie erklärt diese und weitere mit der Gravitation zusammenhängenden Phänomene wie die Gezeiten auf der Erde und Bahnstörungen des Mondes und der Planeten mit großer Genauigkeit. Verbleibende Unstimmigkeiten wurden erst Anfang des 20. Jahrhunderts durch die von Albert Einstein entwickelte allgemeine Relativitätstheorie geklärt.
Geschichte
Eine erste intensivere Beschäftigung Newtons mit der physikalischen Beschreibung der Planetenbahnen und der Rolle der Schwerkraft, die in seinem annus mirabilis 1665/66 erfolgte, enthielt teilweise das Konzept einer quadratisch abnehmenden Schwerkraft. Newton begründete das aber nicht bzw. ging von falschen Annahmen aus, insbesondere noch nicht vom Gedanken der universellen (also außerirdischen) Wirkung der Schwerkraft.[1]
Vom Jahr 1678 an beschäftigte Newton sich, in Zusammenarbeit mit Hooke und Flamsteed, intensiv mit Mechanik, insbesondere mit den keplerschen Gesetzen. In einem Briefwechsel mit Newton erwähnte Hooke seine Theorie der Planetenbewegung, darin war die Rede von einer Anziehungskraft, die mit der Entfernung abnimmt; in Newtons Antwort ging dieser von konstanter Schwerkraft aus. Dieser Briefwechsel war Ausgangspunkt des späteren Plagiatsvorwurfs von Hooke an Newton. Newton räumte dabei ein, dass Hooke ihn auf den richtigen Weg geführt habe: Sowohl die Idee, dass die Bahnellipse von einer (mit dem Quadrat der Entfernung von einem Brennpunkt) abnehmenden Anziehungskraft herrührt, stamme von Hooke wie auch der Gedanke, dass dieses Konzept auch für planetarische Bewegungen anwendbar ist. Hookes Vorschlag abnehmender Schwerkraft beruhte allerdings auf Intuition und nicht – wie bei Newton – auf Beobachtung und logischer Ableitung.
Seine vorläufigen Ergebnisse veröffentlichte Newton 1684 unter dem Titel De Motu Corporum. Darauf aufbauend legte er 1687 in seinem dreibändigen Werk Philosophiae Naturalis Principia Mathematica (Mathematische Grundlagen der Naturphilosophie) die Grundsteine der klassischen Mechanik. Darin formulierte Newton die drei Newtonschen Gesetze der Bewegung und das Gravitationsgesetz, Letzteres allerdings nicht in der knappen Form wie am Anfang dieses Artikels wiedergegeben, sondern über mehrere Abschnitte verteilt. Er begründete die Gesetze ausführlich unter erstmaliger Verwendung der von ihm geschaffenen geometrischen Form der Infinitesimalrechnung. Der dritte Teil des Werkes beschäftigt sich unter dem Titel Über das Weltsystem mit der Anwendung der neuen Gesetze auf die tatsächlichen Bewegungen von Himmelskörpern, wobei Newton seine Berechnungen mit einer Vielzahl von Messdaten anderer Naturforscher vergleicht und auf diese Weise die Richtigkeit seiner theoretischen Herleitungen belegt.
Henry Cavendish gelang es 1797 als Erstem, in einem Experiment mit einer empfindlichen Drehwaage die gegenseitige Anziehung zweier Körper bekannter Masse experimentell zu messen,[2] wie es aus dem Newtonschen Gravitationsgesetz folgt. Der Messapparat ist ähnlich der Torsionswaage, mit der Charles Augustin de Coulomb 1785 die elektrostatische Anziehung und Abstoßung untersucht hatte, sie stammt ursprünglich von dem Geologen John Michell. Für den Nachweis der Gravitation musste Cavendish den Einfluss kleinster Störungen ausschließen, beispielsweise bediente er deshalb sein Experiment aus einem anderen Raum und machte die Ablesungen mit einem Fernrohr.
In der heute gebräuchlichen expliziten Form wurde das Gravitationsgesetz nicht von Newton selbst, sondern erst 1873, also 200 Jahre später, von Alfred Cornu und Jean-Baptistin Baille formuliert.[3][4] Bis dahin hatte man das Newtonsche Gravitationsgesetz lediglich in seiner ursprünglichen Form verwendet, d. h. in Gestalt der Proportionalitäten $ F\propto m_{1}\ ,\ F\propto m_{2}\ ,\ F\propto r^{-2} $, und ohne Definition einer „Gravitationskonstanten“.
Das Newtonsche Gravitationsgesetz ermöglichte eine wesentlich genauere Berechnung der Positionen der Planeten als früher. Die nach Ptolomäus oder Kopernikus berechneten Positionen wichen oftmals um $ 10^{\prime } $ (das entspricht 1/3 Monddurchmesser) von den Beobachtungen ab, die nach den keplerschen Gesetzen berechneten noch um bis zu $ 1^{\prime } $.[5] Dagegen gelang es mithilfe der Newtonschen Himmelsmechanik, diese als Bahnstörungen bezeichneten Abweichungen auf die Anziehung durch die anderen Planeten zurückzuführen. Im Fall des Uranus wurde daraus sogar auf die Existenz eines bis dahin unbekannten Planeten, des Neptun, geschlossen, dessen ungefähre Position erstmals von Urbain Le Verrier aus den genauen Werten der Bahnstörung berechnet wurde[6]. Kurz danach entdeckte Johann Gottfried Galle den neuen Planeten in einer Entfernung von nur einem Bogengrad von der Vorhersage.[7] Jedoch ließ sich die später entdeckte Periheldrehung der Bahn des Merkur mit der gleichen Methode nur zu etwa 90 % erklären. Für die volle Erklärung musste erst die allgemeine Relativitätstheorie entwickelt werden. Diese weitaus umfassendere Theorie enthält das Newtonsche Gravitationsgesetz als denjenigen Grenzfall, der nur für hinreichend kleine Massendichten und Geschwindigkeiten gilt.
Mathematische Formulierung
Massenpunkte
Der Betrag der Kraft zwischen zwei Massepunkten $ m_{1} $ und $ m_{2} $ im Abstand $ r $ ist
- $ F=G{\frac {m_{1}m_{2}}{r^{2}}} $
Die Größe $ G $ ist die Gravitationskonstante. Die auf die beiden Massen wirkenden Kräfte haben denselben Betrag und zeigen jeweils auf den anderen Massepunkt (siehe Abbildung). Das Newtonsche Gravitationsgesetz beschreibt damit im Gegensatz zum mathematisch ähnlichen coulombschen Gesetz eine immer anziehende Kraft.
Vektoriell
In vektorieller Form gilt für die auf Massepunkt 1 wirkende Kraft $ {\vec {F}}_{1} $
- $ {\vec {F}}_{1}=G{\frac {m_{1}m_{2}}{r^{3}}}{\vec {r}}_{12}=G{\frac {m_{1}m_{2}}{|{\vec {r}}_{2}-{\vec {r}}_{1}|^{3}}}({\vec {r}}_{2}-{\vec {r}}_{1}) $,
wobei $ {\vec {r}}_{1} $ und $ {\vec {r}}_{2} $ die Positionen (Ortsvektoren) der beiden Massepunkte sind.[8]
$ {\vec {F}}_{2} $ zeigt auf Massepunkt 1 und ist der Gegenvektor zu $ {\vec {F}}_{1} $:
$ {\vec {F}}_{2}=-{\vec {F}}_{1} $.
Wird der Massepunkt 1 von mehreren Massepunkten 2, 3, … , n angezogen, so addieren sich die einzelnen Kräfte zur auf Massepunkt 1 wirkenden Gesamtkraft
- $ {\vec {F}}_{1}=Gm_{1}\sum _{i=2}^{n}m_{i}{\frac {{\vec {r}}_{i}-{\vec {r}}_{1}}{|{\vec {r}}_{i}-{\vec {r}}_{1}|^{3}}} $
Gravitationsbeschleunigung
Daraus resultiert nach dem zweiten Newtonschen Axiom eine Beschleunigung mit dem Betrag
- $ a_{1}={\frac {F_{1}}{m_{1}}} $,
die auch Gravitationsbeschleunigung oder Gravitationsfeldstärke am Ort der Masse $ m_{1} $ genannt wird (siehe Gravitationsfeld).
Zwei Punktmassen $ m_{1} $ und $ m_{2} $ erfahren im Abstand $ r $ bei Abwesenheit anderer Kräfte durch das Newtonsche Gravitationsgesetz die Beschleunigungen:
- $ a_{1}={\frac {F}{m_{1}}}=G{\frac {m_{2}}{r^{2}}}\qquad {\text{bzw.}}\qquad a_{2}={\frac {F}{m_{2}}}=G{\frac {m_{1}}{r^{2}}} $
Die Masse $ m_{1} $ zieht die Masse $ m_{2} $ an und umgekehrt. Beide Massen werden zum gemeinsamen Schwerpunkt hin beschleunigt. Von einem der Körper aus gesehen bewegt sich der andere mit einer Beschleunigung, die die Summe der Einzelbeschleunigungen ist:
- $ a_{1}+a_{2}=G\,{\frac {m_{1}+m_{2}}{r^{2}}} $
Falls nun eine der Massen viel kleiner ist als die andere, reicht es näherungsweise aus, nur die größere Masse zu berücksichtigen. So hat die Erde viel mehr Masse als ein Apfel, ein Mensch oder ein LKW, sodass es für alle diese Objekte reicht, die Masse der Erde in die Gleichung für die Beschleunigung einzusetzen. Alle drei Objekte werden, wenn sie sich an demselben Ort befinden, gleich stark in Richtung Erdmitte beschleunigt. Sie fallen gleich schnell und in dieselbe Richtung. Wenn man jedoch ein Doppelsternsystem betrachtet, muss man beide Sternmassen berücksichtigen, weil sie etwa gleich groß sind.
Wenn sich $ r $ während der Bewegung eines Objektes nur sehr geringfügig verändert, ist die Gravitationsbeschleunigung praktisch konstant, etwa bei einem Gegenstand nahe der Erdoberfläche, der nur einige Meter tief fällt, also verschwindend wenig im Vergleich zum Erdradius von r = ca. 6370 km. In einem hinreichend kleinen Bereich kann also das Gravitationsfeld als homogen betrachtet werden. Wenn man die Veränderung der Gravitationskraft mit dem Abstand nicht vernachlässigen kann, ist eine Berechnung beispielsweise der Auftreffgeschwindigkeit eines frei fallenden Körpers mithilfe der Integralrechnung möglich, d. h. über das Gravitationspotential
- $ \Phi (r)=-{\frac {Gm}{r}} $.
Ausgedehnte Körper
Reale Körper sind keine Punktmassen, sondern haben eine räumliche Ausdehnung. Da das Gravitationsgesetz linear in den Massen ist, kann der Körper gedanklich in kleine Teile zerlegt werden, deren Beiträge, wie im vorigen Abschnitt gezeigt, vektoriell addiert werden können. Beim Grenzübergang zu unendlich kleinen Teilen ergibt sich statt einer Summe ein Integral.
Auf diese Weise kann unter anderem gezeigt werden, dass ein Objekt mit sphärisch symmetrischer Massenverteilung im Außenraum dieselbe Gravitationswirkung hat, als wäre seine gesamte Masse in seinem Schwerpunkt vereinigt. Daher können ausgedehnte Himmelskörper näherungsweise als Massenpunkte behandelt werden. Im Innern einer elliptischen oder kugelsymmetrischen homogenen Massenverteilung, z. B. einer Hohlkugel, ist die von dieser Masse ausgehende Gravitationskraft null. Daraus folgt, dass in einem beliebigen Abstand $ r $ vom Mittelpunkt einer kugelsymmetrischen Massenverteilung die Gravitationskraft genau von dem Anteil der Gesamtmasse erzeugt wird, der innerhalb einer Kugel mit dem Radius $ r $ liegt. Newton hat dieses Theorem (das auch als Newtonsches Schalentheorem bezeichnet wird) in seiner Philosophiae Naturalis Principia Mathematica bewiesen. Für nicht elliptisch symmetrische Körper oder inhomogene Massenverteilungen gilt das Theorem im Allgemeinen nicht. Ebenso ist zu beachten, dass die Gravitation keine Gegenkraft besitzt, also nicht abgeschirmt werden kann. Das tatsächliche Gravitationsfeld in einer Hohlkugel wäre somit nicht null, da im Inneren natürlich die Gravitationskräfte aller anderen im Universum vorhandenen Massen wirken würden – nur die Kugelschale selbst würde nichts beitragen.
Grenzen der Theorie
Obwohl es für praktische Zwecke hinreichend genau ist, ist das Newtonsche Gravitationsgesetz nur eine Näherung für schwache und zeitunabhängige Gravitationsfelder. Für starke Felder verwendet man die genauere Beschreibung mittels der allgemeinen Relativitätstheorie, aus der die Poisson-Gleichung der klassischen Gravitationstheorie und damit auch das Newtonsche Gravitationsgesetz direkt hergeleitet werden kann, wenn man nur annimmt, dass es sich bei der Gravitation um ein konservatives Feld handelt. Man bezeichnet das Gesetz daher heute oft als Grenzfall kleiner Felder. Die allgemeine Relativitätstheorie löst insbesondere auch die hier beschriebenen Probleme der Newtonschen Gravitationstheorie.
Theoretische Grenzen
- Die Newtonsche Theorie ist eine effektive Theorie, das bedeutet, sie gibt weder eine Ursache für die Gravitationskraft an, noch erklärt sie, wie die Gravitation über die Entfernung wirken kann. Viele Zeitgenossen, darunter Newton selbst und auch noch Leonhard Euler, lehnten die Möglichkeit einer unmittelbaren Fernwirkung durch den leeren Raum ab. Um diese Erklärungslücke zu schließen, wurde die sogenannte Le-Sage-Gravitation als Modell entwickelt, das sich jedoch nie wirklich durchsetzen konnte.
- Die Newtonsche Theorie setzt voraus, dass sich die Gravitationswirkung unendlich schnell ausbreitet, damit die keplerschen Gesetze erfüllt sind. Dies führt zu Konflikten mit der speziellen Relativitätstheorie. Diese fordert nämlich, dass sich auch die Gravitation nur mit Lichtgeschwindigkeit ausbreitet.
- Die Äquivalenz von träger und schwerer Masse ist in der Newtonschen Mechanik nicht erklärt.
Widersprüche zur Beobachtung
- Die Newtonsche Theorie erklärt nicht vollständig die Periheldrehung der Planetenumlaufbahnen, besonders des Merkur. Bei diesem beträgt der Unterschied zwischen der nach der Newtonschen Theorie berechneten und der beobachteten Periheldrehung 43 Bogensekunden pro Jahrhundert.
- Ob Licht im Gravitationsfeld abgelenkt wird oder nicht, hängt in der Newtonschen Theorie davon ab, welche Natur dem Licht zugeschrieben wird. Wird es als elektromagnetische Welle aufgefasst, dann ergibt sich keine Ablenkung. Wird es jedoch gemäß der Korpuskeltheorie als massebehaftetes Teilchen aufgefasst, dann ergibt sich gemäß dem Newtonschen Gravitationsgesetz eine Lichtablenkung, wobei aus der Bewegungsgleichung eine Vorhersage gemacht werden kann, die unabhängig von der Masse ist und somit auch im Grenzfall verschwindender Masse gültig bleibt. Dieser Wert beträgt jedoch nur die Hälfte der tatsächlich beobachteten Ablenkung.
Für beide Effekte ergibt sich der gemessene Wert korrekt aus den Gleichungen der allgemeinen Relativitätstheorie.
Literatur
- Wolfgang Demtröder: Experimentalphysik 1. Springer, 2006, ISBN 978-3-540-26034-9.
Einzelnachweise
- ↑ Jürgen Fertig: Isaac Newtons erster Mondtest, der keiner war! (PDF; 4,5 MB). In: Mitteilungen der Deutschen Geophysikalischen Gesellschaft e.V. 1/2016.
- ↑ Henry Cavendish: Experiments to determine the Density of the Earth. (PDF) 1798 (englisch).
- ↑ Clive Speake, Terry Quinn: The search for Newton’s constant. In: Physics Today. Band 67, Nr. 7, 2014, S. 27, doi:10.1063/PT.3.2447.
- ↑ A. Cornu, J. Baille: Détermination nouvelle de la constante de l’attraction et de la densité moyennede la Terre. In: Comptes Rendus Hebd. Seances Acad. Sci. Band 76, 1873, S. 954 (online [abgerufen am 3. April 2019]).
- ↑ Gearhart, C.A.: Epicycles, eccentrics, and ellipses: The predictive capabilities of Copernican planetary models. In: Archive for History of Exact Sciences. Band 32, Nr. 3, 1985, S. 207–222, doi:10.1007/BF00348449.
- ↑ James Lequeux: Le Verrier — Magnificent and Detestable Astronomer. Springer Verlag, 2013. S. 23.
- ↑ Thomas Bührke: Sternstunden der Astronomie. Von Kopernikus bis Oppenheimer. München 2001, S. 150.
- ↑ Walter Greiner: Klassische Mechanik 1. Kinematik und Dynamik der Punktteilchen. Relativität. 8., überarb. u. erw. Auflage. Harri Deutsch, Frankfurt 2008, ISBN 978-3-8171-1815-1, S. 4.