Jürgen Ehlers (Physiker): Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Wikipedia:GND in Wikipedia weicht von GND in Wikidata ab
- Astrophysiker
- Physiker (20. Jahrhundert)
- Mitglied der Akademie der Wissenschaften und der Literatur
- Mitglied der Bayerischen Akademie der Wissenschaften
- Mitglied der Berlin-Brandenburgischen Akademie der Wissenschaften
- Mitglied der Leopoldina (20. Jahrhundert)
- Wissenschaftliches Mitglied der Max-Planck-Gesellschaft
- Hochschullehrer (University of Texas at Austin)
- Hochschullehrer (Ludwig-Maximilians-Universität München)
- Deutscher
- Geboren 1929
- Gestorben 2008
- Mann
- Träger der Max-Planck-Medaille
imported>JamesP K (fixed typo) |
imported>Antonsusi K |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:Juergen Ehlers.jpg|mini|Jürgen Ehlers anlässlich der Verleihung der Medaille der [[Karls-Universität Prag]]]] | [[Datei:Juergen Ehlers.jpg|mini|Jürgen Ehlers anlässlich der Verleihung der Medaille der [[Karls-Universität Prag]]]] | ||
'''Jürgen Ehlers''' (* [[29. Dezember]] [[1929]] in [[Hamburg]]; † [[20. Mai]] [[2008]] in [[Potsdam]]) war ein | '''Jürgen Ehlers''' (* [[29. Dezember]] [[1929]] in [[Hamburg]]; † [[20. Mai]] [[2008]] in [[Potsdam]]) war ein | ||
deutscher [[Physiker]], der wichtige Beiträge zur einsteinschen [[Allgemeine Relativitätstheorie|Allgemeinen Relativitätstheorie]] geliefert hat. Während seiner wissenschaftlichen Ausbildung und danach arbeitete er zunächst bei [[Pascual Jordan]] in [[Hamburg]]. Anschließend war er [[Dozent]] und [[Professor]], ehe er an das [[Max-Planck-Institut für Astrophysik]] nach [[München]] berufen wurde. | deutscher [[Physiker]], der wichtige Beiträge zur einsteinschen [[Allgemeine Relativitätstheorie|Allgemeinen Relativitätstheorie]] geliefert hat. Während seiner wissenschaftlichen Ausbildung und danach arbeitete er zunächst bei [[Pascual Jordan]] in [[Hamburg]]. Anschließend war er [[Dozent]] und [[Professor]], ehe er an das [[Max-Planck-Institut für Astrophysik]] nach [[München]] berufen wurde. | ||
| Zeile 18: | Zeile 18: | ||
== Wissenschaftliche Arbeit == | == Wissenschaftliche Arbeit == | ||
Ehlers beschäftigte sich mit Fragen der Allgemeinen Relativitätstheorie und der [[Kosmologie]], unter anderem an der Theorie der [[Gravitationswelle]]n. | Ehlers beschäftigte sich mit Fragen der Allgemeinen Relativitätstheorie und der [[Kosmologie]], unter anderem an der Theorie der [[Gravitationswelle]]n. | ||
In seiner Doktorarbeit untersuchte er die exakten Lösungen der einsteinschen Gleichungen für Universen, die einfach genug sind, um explizite Lösungen zu erlauben. Da jedoch die allgemein relativistischen Gesetze [[Kovarianz (Physik)|kovariant]] und damit unabhängig von den gewählten [[Koordinatensystem]]en sind, könnten exakt gleiche Modell-Universen in unterschiedlichen Beschreibungen definiert werden. Ehlers suchte nach Wegen, diese Beschreibungen [[Symmetrie (Physik)|invariant]] zu charakterisieren, so dass sie nicht mehr von den gewählten Koordinatensystemen abhängen und ihre Gleichheit offenbar wird. Dazu untersuchte er die immanenten geometrischen Eigenschaften der bekannten exakten Lösungen der einsteinschen Gleichungen<ref>Bernd Schmidt: ''Vorwort.'' In: ''Einstein's Field Equations and their Physical Implications. Selected Essays in Honour of Jürgen Ehlers.'' Springer, Berlin 2000, ISBN 3-540-67073-4, S. 1–126.</ref>. | In seiner Doktorarbeit untersuchte er die exakten Lösungen der einsteinschen Gleichungen für Universen, die einfach genug sind, um explizite Lösungen zu erlauben. Da jedoch die allgemein relativistischen Gesetze [[Kovarianz (Physik)|kovariant]] und damit unabhängig von den gewählten [[Koordinatensystem]]en sind, könnten exakt gleiche Modell-Universen in unterschiedlichen Beschreibungen definiert werden. Ehlers suchte nach Wegen, diese Beschreibungen [[Symmetrie (Physik)|invariant]] zu charakterisieren, so dass sie nicht mehr von den gewählten Koordinatensystemen abhängen und ihre Gleichheit offenbar wird. Dazu untersuchte er die immanenten geometrischen Eigenschaften der bekannten exakten Lösungen der einsteinschen Gleichungen<ref>Bernd Schmidt: ''Vorwort.'' In: ''Einstein's Field Equations and their Physical Implications. Selected Essays in Honour of Jürgen Ehlers.'' Springer, Berlin 2000, ISBN 3-540-67073-4, S. 1–126.</ref>. | ||
=== Gravitationswellen und Schwarze Löcher === | === Gravitationswellen und Schwarze Löcher === | ||
Später veröffentlichte Ehlers Arbeiten, die die Ideen seiner Doktorarbeit weiter verfolgten. Mit [[Pascual Jordan]] und [[Wolfgang Kundt]] beschäftigte er sich mit der systematischen Erfassung und den Charakteristiken der exakten Lösungen zu Einsteins Gleichungen der Allgemeinen Relativitätstheorie, wobei die Autoren ausgefeilte Methoden der [[Differentialgeometrie]] benutzten, u. a. die [[Petrov-Klassifikation]] (nach [[Alexei Sinowjewitsch Petrow|Alexei Petrow]]) der [[Weyl-Tensor]]en (also denjenigen Anteilen des die [[Allgemeine Relativitätstheorie#Grundlegende Konzepte|Raumzeit-Krümmung]] beschreibenden [[Riemann-Tensor]]s, der nicht durch die Einstein-Gleichungen beschränkt ist), [[Isometrie]]-Gruppen und [[Konforme Abbildung|konformer Transformationen]]. Hierbei entstand die erstmalige Definition und Klassifikation einer Klasse besonders einfacher Gravitationswellen, der [[pp-Welle]]n. Mit Rainer K. Sachs und Manfred Trümper befasste er sich mit Vakuumlösungen zur [[Gravitationsstrahlung]], die spezielle algebraische Eigenschaften besitzen und im [[Bispinor-Darstellung|Bispinor-Formalismus]] ausgedrückt wurden. Ehlers legte bei seinen Untersuchungen zu exakten Lösungen auch die geometrischen Eigenschaften von Lichtbündeln ([[Kongruenz (Geometrie)|Kongruenz]]en) mit Expansion und allgemeiner Deformation ([[Levi-Civitta-Zusammenhang|Torsion]] und [[Scherung (Geometrie)|Scherung]]) systematisch dar. Die mathematischen Hilfsmittel, die hierbei entwickelt wurden, halfen später [[Roy Kerr]] bei der Entdeckung der [[Kerr-Metrik|Kerr-Lösung]] für rotierende [[Schwarzes Loch|Schwarze Löcher]], einer wichtigen exakten Lösung zu Einsteins Gleichungen. In der letzten Arbeit dieser Phase befasste sich Ehlers mit der allgemein-relativistischen Behandlung [[Kontinuumsmechanik|kontinuierlicher Medien]]. | Später veröffentlichte Ehlers Arbeiten, die die Ideen seiner Doktorarbeit weiter verfolgten. Mit [[Pascual Jordan]] und [[Wolfgang Kundt]] beschäftigte er sich mit der systematischen Erfassung und den Charakteristiken der exakten Lösungen zu Einsteins Gleichungen der Allgemeinen Relativitätstheorie, wobei die Autoren ausgefeilte Methoden der [[Differentialgeometrie]] benutzten, u. a. die [[Petrov-Klassifikation]] (nach [[Alexei Sinowjewitsch Petrow|Alexei Petrow]]) der [[Weyl-Tensor]]en (also denjenigen Anteilen des die [[Allgemeine Relativitätstheorie#Grundlegende Konzepte|Raumzeit-Krümmung]] beschreibenden [[Riemann-Tensor]]s, der nicht durch die Einstein-Gleichungen beschränkt ist), [[Isometrie]]-Gruppen und [[Konforme Abbildung|konformer Transformationen]]. Hierbei entstand die erstmalige Definition und Klassifikation einer Klasse besonders einfacher Gravitationswellen, der [[pp-Welle]]n. Mit Rainer K. Sachs und Manfred Trümper befasste er sich mit Vakuumlösungen zur [[Gravitationsstrahlung]], die spezielle algebraische Eigenschaften besitzen und im [[Bispinor-Darstellung|Bispinor-Formalismus]] ausgedrückt wurden. Ehlers legte bei seinen Untersuchungen zu exakten Lösungen auch die geometrischen Eigenschaften von Lichtbündeln ([[Kongruenz (Geometrie)|Kongruenz]]en) mit Expansion und allgemeiner Deformation ([[Levi-Civitta-Zusammenhang|Torsion]] und [[Scherung (Geometrie)|Scherung]]) systematisch dar. Die mathematischen Hilfsmittel, die hierbei entwickelt wurden, halfen später [[Roy Kerr]] bei der Entdeckung der [[Kerr-Metrik|Kerr-Lösung]] für rotierende [[Schwarzes Loch|Schwarze Löcher]], einer wichtigen exakten Lösung zu Einsteins Gleichungen. In der letzten Arbeit dieser Phase befasste sich Ehlers mit der allgemein-relativistischen Behandlung [[Kontinuumsmechanik|kontinuierlicher Medien]]. | ||
Ein anderer Teil von Jürgen Ehlers Doktorarbeit erwies sich ebenfalls als fruchtbar: Er befasste sich dabei mit dem Beweis einiger Eigenschaften der Oberfläche von Schwarzen Löchern, die später zum Begriff des [[Ereignishorizont]]s führten. Eine wichtige Folge dieser Eigenschaften war es, dass das Gravitationsfeld innerhalb der Oberfläche nicht statisch sein kann, sondern sich mit der Zeit ändern musste. | Ein anderer Teil von Jürgen Ehlers Doktorarbeit erwies sich ebenfalls als fruchtbar: Er befasste sich dabei mit dem Beweis einiger Eigenschaften der Oberfläche von Schwarzen Löchern, die später zum Begriff des [[Ereignishorizont]]s führten. Eine wichtige Folge dieser Eigenschaften war es, dass das Gravitationsfeld innerhalb der Oberfläche nicht statisch sein kann, sondern sich mit der Zeit ändern musste. | ||
| Zeile 32: | Zeile 32: | ||
Während seiner Forschertätigkeit kümmerte sich Ehlers immer wieder auch um die Grundlagen der Allgemeinen Relativitätstheorie. In den 1960er Jahren arbeitete er mit [[Felix Pirani]] und [[Alfred Schild (Physiker)|Alfred Schild]] an einem konstruktiv-axiomatischen Ansatz zur Allgemeinen Relativitätstheorie, wobei sie einen Weg suchten, die Einsteinsche Theorie aus einer minimalen Zahl Objekte und Axiome abzuleiten. Dazu gehören u. A. [[Ereignis]]se, Lichtstrahlen, Teilchen und frei fallende Teilchen. Am Anfang ist die Raumzeit gemäß ihrem Ansatz eine Menge an Ereignissen, ohne jedwede weitere Strukturierung. Durch die Annahme der grundlegenden als Axiome eingeführten Eigenschaften von Licht und frei fallenden Teilchen wird die [[Differentialtopologie]], [[Konforme Abbildung|konforme Struktur]] und schließlich die metrische Struktur der Raumzeit konstruiert. Der Prozess der Konstruktion orientiert sich an idealisierten Messungen. Im abschließenden Schritt werden die Einsteinschen Gleichungen mit Hilfe der schwächsten zusätzlichen Axiome abgeleitet. Damit entsteht eine Formulierung der Gleichungen, in der die Annahmen, die zur Allgemeinen Relativitätstheorie führen, klar definiert sind. | Während seiner Forschertätigkeit kümmerte sich Ehlers immer wieder auch um die Grundlagen der Allgemeinen Relativitätstheorie. In den 1960er Jahren arbeitete er mit [[Felix Pirani]] und [[Alfred Schild (Physiker)|Alfred Schild]] an einem konstruktiv-axiomatischen Ansatz zur Allgemeinen Relativitätstheorie, wobei sie einen Weg suchten, die Einsteinsche Theorie aus einer minimalen Zahl Objekte und Axiome abzuleiten. Dazu gehören u. A. [[Ereignis]]se, Lichtstrahlen, Teilchen und frei fallende Teilchen. Am Anfang ist die Raumzeit gemäß ihrem Ansatz eine Menge an Ereignissen, ohne jedwede weitere Strukturierung. Durch die Annahme der grundlegenden als Axiome eingeführten Eigenschaften von Licht und frei fallenden Teilchen wird die [[Differentialtopologie]], [[Konforme Abbildung|konforme Struktur]] und schließlich die metrische Struktur der Raumzeit konstruiert. Der Prozess der Konstruktion orientiert sich an idealisierten Messungen. Im abschließenden Schritt werden die Einsteinschen Gleichungen mit Hilfe der schwächsten zusätzlichen Axiome abgeleitet. Damit entsteht eine Formulierung der Gleichungen, in der die Annahmen, die zur Allgemeinen Relativitätstheorie führen, klar definiert sind. | ||
In den 1970er Jahren befasste sich Ehlers gemeinsam mit [[Ekkart Rudolph]] mit der allgemein-relativistischen Behandlung des [[Starrer Körper|starren Körpers]]. Zwar hatte [[Max Born]] bereits 1909 eine Definition eines starren Körpers angegeben, die mit der relativistischen Physik kompatibel ist, doch beruht diese Definition auf Annahmen, die in der allgemein-relativistischen Raumzeit nicht mehr erfüllt und auch zu restriktiv sind. Ehlers und Rudolph verallgemeinerten Borns Definition zu einer einfacher anwendbaren Definition, die sie „Pseudo-Festigkeit“ nannten und die eine bessere Näherung des Festigkeitsbegriffs der klassischen Physik darstellt. | In den 1970er Jahren befasste sich Ehlers gemeinsam mit [[Ekkart Rudolph]] mit der allgemein-relativistischen Behandlung des [[Starrer Körper|starren Körpers]]. Zwar hatte [[Max Born]] bereits 1909 eine Definition eines starren Körpers angegeben, die mit der relativistischen Physik kompatibel ist, doch beruht diese Definition auf Annahmen, die in der allgemein-relativistischen Raumzeit nicht mehr erfüllt und auch zu restriktiv sind. Ehlers und Rudolph verallgemeinerten Borns Definition zu einer einfacher anwendbaren Definition, die sie „Pseudo-Festigkeit“ nannten und die eine bessere Näherung des Festigkeitsbegriffs der klassischen Physik darstellt. | ||
Das von ihm 1968 mit P. Geren und Rainer K. Sachs bewiesene Ehlers-Geren-Sachs-Theorem folgert aus der Beobachtung der [[Isotropie]] der [[Kosmische Hintergrundstrahlung|Kosmischen Hintergrundstrahlung]] für alle frei fallenden Beobachter, dass die Kosmologie durch homogene und isotrope [[Friedmann-Lemaître-Robertson-Walker-Metrik|FLRW Metriken]] beschrieben wird. | Das von ihm 1968 mit P. Geren und Rainer K. Sachs bewiesene Ehlers-Geren-Sachs-Theorem folgert aus der Beobachtung der [[Isotropie]] der [[Kosmische Hintergrundstrahlung|Kosmischen Hintergrundstrahlung]] für alle frei fallenden Beobachter, dass die Kosmologie durch homogene und isotrope [[Friedmann-Lemaître-Robertson-Walker-Metrik|FLRW Metriken]] beschrieben wird. | ||
| Zeile 42: | Zeile 42: | ||
=== Frame-Theorie und Newtons Gravitationsmodell === | === Frame-Theorie und Newtons Gravitationsmodell === | ||
Die Ableitung der Gravitationstheorie von [[Isaac Newton]] aus der Allgemeinen Relativitätstheorie stellte Einstein bereits zu Beginn dar und formte daraus Vorhersagen von beobachtbaren Phänomenen, wie der [[Periheldrehung]] des [[Merkur (Planet)|Merkur]]. Spätere Arbeiten von [[Élie Cartan]], [[Kurt Friedrichs]] und anderen wiesen einen konkreteren Weg, wie die Newtonsche Theorie aus der Allgemeinen Relativitätstheorie verstanden werden kann ([[Newton-Cartan-Theorie]]): dazu musste nur ein spezifischer Parameter λ gegen 0 gehen. Ehlers führte diese Arbeiten weiter und verallgemeinerte sie zur Frame-Theorie, einem mathematisch präzisen Weg zur Konstruktion des Newton-Cartan-Grenzwerts nicht nur für die physikalischen Gesetze der Allgemeinen Relativitätstheorie, sondern auch für alle Lösungen der Einsteinschen Gleichungen. Der newtonsche Grenzfall für ein [[Schwarzes Loch]] gemäß der [[Schwarzschild-Lösung]] ist dann ein einfaches Teilchen ohne Ausdehnung. Darüber hinaus können interessante exakte Lösungen für [[Friedmann-Lemaître-Robertson-Walker-Metrik|Friedmann-Lemaître-Raumzeiten]] und das [[Gödel-Universum]] angegeben werden. | Die Ableitung der Gravitationstheorie von [[Isaac Newton]] aus der Allgemeinen Relativitätstheorie stellte Einstein bereits zu Beginn dar und formte daraus Vorhersagen von beobachtbaren Phänomenen, wie der [[Periheldrehung]] des [[Merkur (Planet)|Merkur]]. Spätere Arbeiten von [[Élie Cartan]], [[Kurt Friedrichs]] und anderen wiesen einen konkreteren Weg, wie die Newtonsche Theorie aus der Allgemeinen Relativitätstheorie verstanden werden kann ([[Newton-Cartan-Theorie]]): dazu musste nur ein spezifischer Parameter λ gegen 0 gehen. Ehlers führte diese Arbeiten weiter und verallgemeinerte sie zur Frame-Theorie, einem mathematisch präzisen Weg zur Konstruktion des Newton-Cartan-Grenzwerts nicht nur für die physikalischen Gesetze der Allgemeinen Relativitätstheorie, sondern auch für alle Lösungen der Einsteinschen Gleichungen. Der newtonsche Grenzfall für ein [[Schwarzes Loch]] gemäß der [[Schwarzschild-Lösung]] ist dann ein einfaches Teilchen ohne Ausdehnung. Darüber hinaus können interessante exakte Lösungen für [[Friedmann-Lemaître-Robertson-Walker-Metrik|Friedmann-Lemaître-Raumzeiten]] und das [[Gödel-Universum]] angegeben werden. | ||
Ehlers beteiligte sich daneben an Diskussionen (unter anderem mit [[Peter Havas]]) zur Rückwirkung von Gravitationsstrahlung und untersuchte, wie diese Situation in einer allgemein-relativistischen Theorie systematisch beschrieben werden kann. Dabei fand er, dass die übliche [[Quadrupol]]-Formel für den [[Energiefluss]] für Systeme wie [[Pulsar|Binärpulsare]] (zum Beispiel in dem viel untersuchten ''klassischen'' System [[PSR | Ehlers beteiligte sich daneben an Diskussionen (unter anderem mit [[Peter Havas]]) zur Rückwirkung von Gravitationsstrahlung und untersuchte, wie diese Situation in einer allgemein-relativistischen Theorie systematisch beschrieben werden kann. Dabei fand er, dass die übliche [[Quadrupol]]-Formel für den [[Energiefluss]] für Systeme wie [[Pulsar|Binärpulsare]] (zum Beispiel in dem viel untersuchten ''klassischen'' System [[PSR J1915+1606]], an dem der Nachweis der Gravitationswellen gelang) nicht streng gelöst worden war und eine korrekte Darstellung Terme höherer Ordnung einschließen müsste. | ||
Die Arbeiten zu den newtonschen Grenzwerten der Allgemeinen Relativitätstheorie brachten Ehlers und seinen Mitarbeiter [[Thomas Buchert]] auf die Idee einer systematischen Untersuchung von Störungen und Inhomogenitäten in einem Newton-Kosmos. Buchert schöpfte daraus die Basis seiner allgemein-relativistischen Verallgemeinerung von Inhomogenitäten, mit einer Interpretation der [[Kosmologische Konstante|Kosmologischen Konstante]] – oder in moderner Terminologie die [[Dunkle Energie]] – als einer nichtlinearen Folge der Inhomogenitäten in der allgemein-relativistischen Kosmologie. | Die Arbeiten zu den newtonschen Grenzwerten der Allgemeinen Relativitätstheorie brachten Ehlers und seinen Mitarbeiter [[Thomas Buchert]] auf die Idee einer systematischen Untersuchung von Störungen und Inhomogenitäten in einem Newton-Kosmos. Buchert schöpfte daraus die Basis seiner allgemein-relativistischen Verallgemeinerung von Inhomogenitäten, mit einer Interpretation der [[Kosmologische Konstante|Kosmologischen Konstante]] – oder in moderner Terminologie die [[Dunkle Energie]] – als einer nichtlinearen Folge der Inhomogenitäten in der allgemein-relativistischen Kosmologie. | ||
=== Geschichte und Philosophie der Physik === | === Geschichte und Philosophie der Physik === | ||
Jürgen Ehlers interessierte sich | Jürgen Ehlers interessierte sich auch für Physik- und im weiteren Sinne für Wissenschaftsgeschichte. Er arbeitete bis zu seinem Tod an einem Projekt des [[Max-Planck-Institut für Wissenschaftsgeschichte|Max-Planck-Instituts für Wissenschaftsgeschichte]] zur Geschichte der [[Quantenphysik]], wobei er [[Pascual Jordan]]s wichtige Arbeiten aus den Jahren zwischen 1925 und 1928 untersuchte. | ||
== Mitgliedschaften und Ehrungen == | == Mitgliedschaften und Ehrungen == | ||
* Gründungsmitglied der [[Berlin-Brandenburgische Akademie der Wissenschaften|Berlin-Brandenburgischen Akademie der Wissenschaften]] | * Gründungsmitglied der [[Berlin-Brandenburgische Akademie der Wissenschaften|Berlin-Brandenburgischen Akademie der Wissenschaften]] | ||
* 1970: Invited Speaker auf dem [[Internationaler Mathematikerkongress|Internationalen Mathematikerkongress]] in [[Nizza]] (<math>\mu</math> space statistical mechanics in general relativity theory) | * 1970: Invited Speaker auf dem [[Internationaler Mathematikerkongress|Internationalen Mathematikerkongress]] in [[Nizza]] (<math>\mu</math> space statistical mechanics in general relativity theory) | ||
* 1972: Mitglied der [[Akademie der Wissenschaften und der Literatur]], Mainz | * 1972: Mitglied der [[Akademie der Wissenschaften und der Literatur]], Mainz | ||
* 1975: Mitglied der [[Leopoldina|Deutschen Akademie der Naturforscher Leopoldina]] | * 1975: Mitglied der [[Leopoldina|Deutschen Akademie der Naturforscher Leopoldina]] | ||
* 1979: Mitglied der [[Bayerische Akademie der Wissenschaften|Bayerischen Akademie der Wissenschaften]], München | * 1979: Mitglied der [[Bayerische Akademie der Wissenschaften|Bayerischen Akademie der Wissenschaften]], München | ||
* 1995–1998: Präsident der International Society on General Relativity and Gravitation | * 1995–1998: Präsident der International Society on General Relativity and Gravitation | ||
| Zeile 70: | Zeile 70: | ||
* (Hrsg.): ''Relativity theory and astrophysics.'' American Mathematical Society, 1967. | * (Hrsg.): ''Relativity theory and astrophysics.'' American Mathematical Society, 1967. | ||
* (Hrsg.): ''Isolated gravitational systems in general relativity.'' E. Fermi School, Varenna 1977, North Holland 1979. | * (Hrsg.): ''Isolated gravitational systems in general relativity.'' E. Fermi School, Varenna 1977, North Holland 1979. | ||
* Mit Claus | * Mit [[Claus Lämmerzahl]] (Hrsg.): ''Special relativity: will it survive the next 101 years ?'' Springer 2006 (Heraeus Seminar). | ||
* Mit H. Friedrich (Hrsg.): ''Canonical gravity- from classical to quantum.'' Springer 1994 (Heraeus Seminar). | * Mit H. Friedrich (Hrsg.): ''Canonical gravity- from classical to quantum.'' Springer 1994 (Heraeus Seminar). | ||
* Mit Peter Schneider, E. E. Falco: ''Gravitational Lenses.'' Springer 1992, 1999. | * Mit Peter Schneider, E. E. Falco: ''Gravitational Lenses.'' Springer 1992, 1999. | ||
* Mit [[Wolfgang Kundt]]: ''Exact solutions of gravitational field equations.'' In: L. Witten (Hrsg.): ''Gravitation – introduction to current research.'' Wiley 1962- | * Mit [[Wolfgang Kundt]]: ''Exact solutions of gravitational field equations.'' In: L. Witten (Hrsg.): ''Gravitation – introduction to current research.'' Wiley 1962- | ||
* ''Survey of General Relativity.'' In: Werner Israel (Hrsg.): ''Relativity, Astrophysics and Cosmology.'' Reidel 1973. | * ''Survey of General Relativity.'' In: Werner Israel (Hrsg.): ''Relativity, Astrophysics and Cosmology.'' Reidel 1973. | ||
* ''Beiträge zur relativistischen Dynamik kontinuierlicher Medien'', Abhandlungen der Mathem.-Naturwiss. Klasse, Akademie der Wissenschaften Mainz, Nr.11, 1961, S. 782–837, wieder abgedruckt in: [[George F. R. Ellis]], Malcolm A. H. MacCallum, Andrzej Krasinski (Hrsg.) ''Golden Oldies in General Relativity. Hidden Gems'', Springer Verlag 2013. | * ''Beiträge zur relativistischen Dynamik kontinuierlicher Medien'', Abhandlungen der Mathem.-Naturwiss. Klasse, Akademie der Wissenschaften Mainz, Nr. 11, 1961, S. 782–837, wieder abgedruckt in: [[George F. R. Ellis]], Malcolm A. H. MacCallum, Andrzej Krasinski (Hrsg.) ''Golden Oldies in General Relativity. Hidden Gems'', Springer Verlag 2013. | ||
* Mit [[Pascual Jordan]], Wolfgang Kundt ''Strenge Lösungen der Feldgleichungen der Allgemeinen Relativitätstheorie'', Abhandlungen der Mathem.-Naturwiss. Klasse, Akademie der Wissenschaften Mainz, Nr.2, 1960, S. 21–105. | * Mit [[Pascual Jordan]], Wolfgang Kundt ''Strenge Lösungen der Feldgleichungen der Allgemeinen Relativitätstheorie'', Abhandlungen der Mathem.-Naturwiss. Klasse, Akademie der Wissenschaften Mainz, Nr. 2, 1960, S. 21–105. | ||
* Mit [[Felix Pirani]], [[Alfred Schild (Physiker)|Alfred Schild]] ''The geometry of free fall and light propagation'', in O´Raifeartaigh (Hrsg.) ''General Relativity. Papers in honour of J. L. Synge'', Oxford, Clarendon Press 1972, S. 63–84. | * Mit [[Felix Pirani]], [[Alfred Schild (Physiker)|Alfred Schild]] ''The geometry of free fall and light propagation'', in O´Raifeartaigh (Hrsg.) ''General Relativity. Papers in honour of J. L. Synge'', Oxford, Clarendon Press 1972, S. 63–84. | ||
| Zeile 84: | Zeile 84: | ||
== Weblinks == | == Weblinks == | ||
* {{DNB-Portal|121317374|NAME=Jürgen Ehlers}} | * {{DNB-Portal|121317374|NAME=Jürgen Ehlers}} | ||
* [http://www. | * [http://www.aei.mpg.de/173136/Obituary_by_Ralf_Breuer Nachruf von Reinhard Breuer] | ||
* [http://www.aei.mpg.de/270880/Prof_Dr_Juergen_Ehlers_ist_verstorben Nachruf beim Max Planck Institut] | * [http://www.aei.mpg.de/270880/Prof_Dr_Juergen_Ehlers_ist_verstorben Nachruf beim Max-Planck-Institut] | ||
* [https://www.pro-physik.de/restricted-files/113276 Nachruf von Claus Lämmerzahl und Hermann Nikolai im Physik-Journal], PDF | |||
== Einzelnachweise == | == Einzelnachweise == | ||
| Zeile 102: | Zeile 103: | ||
[[Kategorie:Hochschullehrer (University of Texas at Austin)]] | [[Kategorie:Hochschullehrer (University of Texas at Austin)]] | ||
[[Kategorie:Hochschullehrer (Ludwig-Maximilians-Universität München)]] | [[Kategorie:Hochschullehrer (Ludwig-Maximilians-Universität München)]] | ||
[[Kategorie:Deutscher]] | [[Kategorie:Deutscher]] | ||
[[Kategorie:Geboren 1929]] | [[Kategorie:Geboren 1929]] | ||
[[Kategorie:Gestorben 2008]] | [[Kategorie:Gestorben 2008]] | ||
[[Kategorie:Mann]] | [[Kategorie:Mann]] | ||
[[Kategorie:Träger der Max-Planck-Medaille]] | |||
{{Personendaten | {{Personendaten | ||
Aktuelle Version vom 20. Februar 2022, 20:03 Uhr
Jürgen Ehlers (* 29. Dezember 1929 in Hamburg; † 20. Mai 2008 in Potsdam) war ein deutscher Physiker, der wichtige Beiträge zur einsteinschen Allgemeinen Relativitätstheorie geliefert hat. Während seiner wissenschaftlichen Ausbildung und danach arbeitete er zunächst bei Pascual Jordan in Hamburg. Anschließend war er Dozent und Professor, ehe er an das Max-Planck-Institut für Astrophysik nach München berufen wurde.
Ehlers ist bekannt für seine Klassifizierungen der exakten Lösungen der einsteinschen Feldgleichungen, für das Ehlers-Geren-Sachs-Theorem, für eine Raumzeit-orientierte Darstellung des Phänomens der Gravitationslinsen und für seine Arbeiten zum Zusammenhang zwischen der Allgemeinen Relativitätstheorie und der newtonschen Gravitationstheorie. Zudem versuchte Ehlers, die Wissenschaften allgemeinverständlich zu erklären und interessierte sich für die Geschichte und Philosophie der Physik.
Leben und Werk
Jürgen Ehlers wurde in Hamburg geboren und ging zwischen 1936 und 1949 zur Schule, bevor er von 1949 bis 1955 Physik, Mathematik und Philosophie an der Universität Hamburg studierte. Im Wintersemester legte er die Prüfung für das Lehramt ab, doch ging er anschließend in eine Forschungsgruppe. 1958 wurde er bei Pascual Jordan zur Konstruktion und Charakterisierung der Einsteinschen Gleichungen promoviert. Die Gruppe um Jordan war ursprünglich mit der Modifizierung der einsteinschen Theorie zu einer Skalar-Tensor-Theorie beschäftigt, durch Ehlers wurde der Schwerpunkt wieder auf die Interpretation der ursprünglichen Theorie Einsteins gelegt. Weitere Mitglieder der Gruppe waren Wolfgang Kundt, Engelbert Schücking, Otto Heckmann, Rainer K. Sachs und Manfred Trümper[1]. 1959 war er wissenschaftlicher Assistent von Jordan in Hamburg.
Ehlers habilitierte sich 1961 in Hamburg. Nach Lehr- und Forschungstätigkeiten in Kiel (Lehrauftrag 1961), der Syracuse University (Research Associate 1962/63) und Hamburg (Dozent 1963/64) nahm er Einladungen in die USA an, wo er 1964 bis 1965 als Visiting Associate Professor am Graduate Research Center of the Southwest in Dallas und von 1965 bis 1971 an der University of Texas at Austin wirkte, zunächst als Associate Professor und ab 1967 als Professor der Physik. Gleichzeitig nahm er 1969/70 Gastprofessuren an der Universität Würzburg und der Universität Bonn wahr.
München
1971 erhielt Ehlers einen Ruf an das Max-Planck-Institut für Physik und Astrophysik (MPIAP) in München, nachdem der seinerzeitige Direktor des Instituts, Ludwig Biermann, auf ihn aufmerksam geworden war. Ehlers akzeptierte das Angebot und erhielt gleichzeitig eine Honorarprofessur an der Ludwig-Maximilians-Universität. Am MPIAP leitete er als Wissenschaftliches Mitglied bis 1995 die Arbeitsgruppe Gravitationstheorie. Während seiner Zeit als Direktor arbeitete er am Institut mit zahlreichen Forschern, u. a. Bernd Schmidt, Demetrios Christodoulou, Gary Gibbons, John Stewart und Brandon Carter zusammen. Auch Reinhard Breuer, der spätere Chefredakteur der populärwissenschaftlichen Spektrum der Wissenschaft, war in jener Zeit promovierter wissenschaftlicher Mitarbeiter bei Ehlers.
Potsdam
Schon bald nach der Wiedervereinigung Deutschlands 1990 machte sich Ehlers erfolgreich für ein Max-Planck-Institut stark, das die Forschungsansätze Albert Einsteins untersuchen sollte. 1995 wurde er erster Direktor des neu gegründeten Max-Planck-Instituts für Gravitationsphysik in Potsdam-Golm, wo er bis zu seiner Emeritierung 1998 wirkte. Hier leitete er auch die Forschungsgruppe „Grundlagen und Mathematik der Allgemeinen Relativitätstheorie“. Zudem begründete er eine zweite Gruppe um Bernard Schutz, die sich mit den Gravitationswellen beschäftigte. Nach seiner Emeritierung arbeitete Ehlers bis zu seinem Tod am Institut weiter[2].
Wissenschaftliche Arbeit
Ehlers beschäftigte sich mit Fragen der Allgemeinen Relativitätstheorie und der Kosmologie, unter anderem an der Theorie der Gravitationswellen. In seiner Doktorarbeit untersuchte er die exakten Lösungen der einsteinschen Gleichungen für Universen, die einfach genug sind, um explizite Lösungen zu erlauben. Da jedoch die allgemein relativistischen Gesetze kovariant und damit unabhängig von den gewählten Koordinatensystemen sind, könnten exakt gleiche Modell-Universen in unterschiedlichen Beschreibungen definiert werden. Ehlers suchte nach Wegen, diese Beschreibungen invariant zu charakterisieren, so dass sie nicht mehr von den gewählten Koordinatensystemen abhängen und ihre Gleichheit offenbar wird. Dazu untersuchte er die immanenten geometrischen Eigenschaften der bekannten exakten Lösungen der einsteinschen Gleichungen[3].
Gravitationswellen und Schwarze Löcher
Später veröffentlichte Ehlers Arbeiten, die die Ideen seiner Doktorarbeit weiter verfolgten. Mit Pascual Jordan und Wolfgang Kundt beschäftigte er sich mit der systematischen Erfassung und den Charakteristiken der exakten Lösungen zu Einsteins Gleichungen der Allgemeinen Relativitätstheorie, wobei die Autoren ausgefeilte Methoden der Differentialgeometrie benutzten, u. a. die Petrov-Klassifikation (nach Alexei Petrow) der Weyl-Tensoren (also denjenigen Anteilen des die Raumzeit-Krümmung beschreibenden Riemann-Tensors, der nicht durch die Einstein-Gleichungen beschränkt ist), Isometrie-Gruppen und konformer Transformationen. Hierbei entstand die erstmalige Definition und Klassifikation einer Klasse besonders einfacher Gravitationswellen, der pp-Wellen. Mit Rainer K. Sachs und Manfred Trümper befasste er sich mit Vakuumlösungen zur Gravitationsstrahlung, die spezielle algebraische Eigenschaften besitzen und im Bispinor-Formalismus ausgedrückt wurden. Ehlers legte bei seinen Untersuchungen zu exakten Lösungen auch die geometrischen Eigenschaften von Lichtbündeln (Kongruenzen) mit Expansion und allgemeiner Deformation (Torsion und Scherung) systematisch dar. Die mathematischen Hilfsmittel, die hierbei entwickelt wurden, halfen später Roy Kerr bei der Entdeckung der Kerr-Lösung für rotierende Schwarze Löcher, einer wichtigen exakten Lösung zu Einsteins Gleichungen. In der letzten Arbeit dieser Phase befasste sich Ehlers mit der allgemein-relativistischen Behandlung kontinuierlicher Medien.
Ein anderer Teil von Jürgen Ehlers Doktorarbeit erwies sich ebenfalls als fruchtbar: Er befasste sich dabei mit dem Beweis einiger Eigenschaften der Oberfläche von Schwarzen Löchern, die später zum Begriff des Ereignishorizonts führten. Eine wichtige Folge dieser Eigenschaften war es, dass das Gravitationsfeld innerhalb der Oberfläche nicht statisch sein kann, sondern sich mit der Zeit ändern musste.
Ehlers-Gruppe
Ehlers fand eine duale Symmetrie zwischen verschiedenen Komponenten der Metrik einer stationären Raumzeit, die Lösungen der einsteinschen Gleichungen auf andere Lösungen abbildet. Diese Dualität wurde später verallgemeinert zu einer SL(2)-Symmetrie, die als Ehlers-Gruppe bezeichnet wird. Weitere Verallgemeinerungen führten dann zur Geroch-Gruppe, die aus zwei nicht-kommutierenden Untergruppen besteht, von denen eine die Ehlers-Gruppe ist. Hieraus entwickelte sich die Idee der „verborgenen Symmetrien“, die eine wichtige Rolle in Kaluza-Klein-Theorie-Erweiterungen der Allgemeinen Relativitätstheorie spielen sowie deren Verallgemeinerungen, wie der elf-dimensionalen Supergravitation.
Grundlegende Konzepte der Allgemeinen Relativitätstheorie
Während seiner Forschertätigkeit kümmerte sich Ehlers immer wieder auch um die Grundlagen der Allgemeinen Relativitätstheorie. In den 1960er Jahren arbeitete er mit Felix Pirani und Alfred Schild an einem konstruktiv-axiomatischen Ansatz zur Allgemeinen Relativitätstheorie, wobei sie einen Weg suchten, die Einsteinsche Theorie aus einer minimalen Zahl Objekte und Axiome abzuleiten. Dazu gehören u. A. Ereignisse, Lichtstrahlen, Teilchen und frei fallende Teilchen. Am Anfang ist die Raumzeit gemäß ihrem Ansatz eine Menge an Ereignissen, ohne jedwede weitere Strukturierung. Durch die Annahme der grundlegenden als Axiome eingeführten Eigenschaften von Licht und frei fallenden Teilchen wird die Differentialtopologie, konforme Struktur und schließlich die metrische Struktur der Raumzeit konstruiert. Der Prozess der Konstruktion orientiert sich an idealisierten Messungen. Im abschließenden Schritt werden die Einsteinschen Gleichungen mit Hilfe der schwächsten zusätzlichen Axiome abgeleitet. Damit entsteht eine Formulierung der Gleichungen, in der die Annahmen, die zur Allgemeinen Relativitätstheorie führen, klar definiert sind.
In den 1970er Jahren befasste sich Ehlers gemeinsam mit Ekkart Rudolph mit der allgemein-relativistischen Behandlung des starren Körpers. Zwar hatte Max Born bereits 1909 eine Definition eines starren Körpers angegeben, die mit der relativistischen Physik kompatibel ist, doch beruht diese Definition auf Annahmen, die in der allgemein-relativistischen Raumzeit nicht mehr erfüllt und auch zu restriktiv sind. Ehlers und Rudolph verallgemeinerten Borns Definition zu einer einfacher anwendbaren Definition, die sie „Pseudo-Festigkeit“ nannten und die eine bessere Näherung des Festigkeitsbegriffs der klassischen Physik darstellt.
Das von ihm 1968 mit P. Geren und Rainer K. Sachs bewiesene Ehlers-Geren-Sachs-Theorem folgert aus der Beobachtung der Isotropie der Kosmischen Hintergrundstrahlung für alle frei fallenden Beobachter, dass die Kosmologie durch homogene und isotrope FLRW Metriken beschrieben wird.
Gravitationslinsen
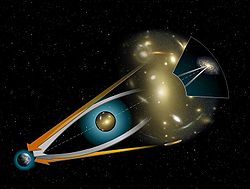
In den 1980er Jahren wandte sich Ehlers zusammen mit Peter Schneider der Erforschung der Grundlagen von Gravitationslinsen zu. Ein Ergebnis war eine 1992 gemeinsam mit Emilio Falco veröffentlichte Studie, die erstmals eine systematische Darstellung sowohl der theoretischen Ergebnisse als auch der Beobachtungsdaten brachte. Aus der Sicht der Astronomie werden Gravitationslinsen oft als quasi-newtonsche Näherung eingeführt, bei der also das Gravitationsfeld klein und die Ablenkung infinitesimal ist – für die meisten Beobachtungen ist dies auch ausreichend. In ihrer Publikation entwickelten die Forscher jedoch eine vollständige und durchgängige Beschreibung von Gravitationslinsen mit rein allgemein-relativistischen Mitteln.
Frame-Theorie und Newtons Gravitationsmodell
Die Ableitung der Gravitationstheorie von Isaac Newton aus der Allgemeinen Relativitätstheorie stellte Einstein bereits zu Beginn dar und formte daraus Vorhersagen von beobachtbaren Phänomenen, wie der Periheldrehung des Merkur. Spätere Arbeiten von Élie Cartan, Kurt Friedrichs und anderen wiesen einen konkreteren Weg, wie die Newtonsche Theorie aus der Allgemeinen Relativitätstheorie verstanden werden kann (Newton-Cartan-Theorie): dazu musste nur ein spezifischer Parameter λ gegen 0 gehen. Ehlers führte diese Arbeiten weiter und verallgemeinerte sie zur Frame-Theorie, einem mathematisch präzisen Weg zur Konstruktion des Newton-Cartan-Grenzwerts nicht nur für die physikalischen Gesetze der Allgemeinen Relativitätstheorie, sondern auch für alle Lösungen der Einsteinschen Gleichungen. Der newtonsche Grenzfall für ein Schwarzes Loch gemäß der Schwarzschild-Lösung ist dann ein einfaches Teilchen ohne Ausdehnung. Darüber hinaus können interessante exakte Lösungen für Friedmann-Lemaître-Raumzeiten und das Gödel-Universum angegeben werden.
Ehlers beteiligte sich daneben an Diskussionen (unter anderem mit Peter Havas) zur Rückwirkung von Gravitationsstrahlung und untersuchte, wie diese Situation in einer allgemein-relativistischen Theorie systematisch beschrieben werden kann. Dabei fand er, dass die übliche Quadrupol-Formel für den Energiefluss für Systeme wie Binärpulsare (zum Beispiel in dem viel untersuchten klassischen System PSR J1915+1606, an dem der Nachweis der Gravitationswellen gelang) nicht streng gelöst worden war und eine korrekte Darstellung Terme höherer Ordnung einschließen müsste.
Die Arbeiten zu den newtonschen Grenzwerten der Allgemeinen Relativitätstheorie brachten Ehlers und seinen Mitarbeiter Thomas Buchert auf die Idee einer systematischen Untersuchung von Störungen und Inhomogenitäten in einem Newton-Kosmos. Buchert schöpfte daraus die Basis seiner allgemein-relativistischen Verallgemeinerung von Inhomogenitäten, mit einer Interpretation der Kosmologischen Konstante – oder in moderner Terminologie die Dunkle Energie – als einer nichtlinearen Folge der Inhomogenitäten in der allgemein-relativistischen Kosmologie.
Geschichte und Philosophie der Physik
Jürgen Ehlers interessierte sich auch für Physik- und im weiteren Sinne für Wissenschaftsgeschichte. Er arbeitete bis zu seinem Tod an einem Projekt des Max-Planck-Instituts für Wissenschaftsgeschichte zur Geschichte der Quantenphysik, wobei er Pascual Jordans wichtige Arbeiten aus den Jahren zwischen 1925 und 1928 untersuchte.
Mitgliedschaften und Ehrungen
- Gründungsmitglied der Berlin-Brandenburgischen Akademie der Wissenschaften
- 1970: Invited Speaker auf dem Internationalen Mathematikerkongress in Nizza (
- 1972: Mitglied der Akademie der Wissenschaften und der Literatur, Mainz
- 1975: Mitglied der Deutschen Akademie der Naturforscher Leopoldina
- 1979: Mitglied der Bayerischen Akademie der Wissenschaften, München
- 1995–1998: Präsident der International Society on General Relativity and Gravitation
- 2002: Max-Planck-Medaille der Deutschen Physikalischen Gesellschaft
- 2005: Volta-Medaille in Gold der Universität Pavia
- 2007: Medaille der Karls-Universität Prag
Familie
Ehlers war mit Anita Ehlers verheiratet. Sie studierte Physik und Mathematik in Hamburg, wo sie ihren Mann kennenlernte. In München war sie als Lehrerin tätig und wurde durch Übersetzungen populärwissenschaftlicher Bücher bekannt. Ihre eigene Liebe zur Musik führte sie zu Arbeiten am Thema „Einstein und die Musik“. Bekannt ist auch ihr Buch „Liebes Hertz! Physiker und Mathematiker in Anekdoten“.
Schriften
- Mit Gerhard Börner, Heinrich Meyer (Hrsg.): Vom Urknall zum komplexen Universum: die Kosmologie der Gegenwart. Piper, 1993.
- Mit Gerhard Börner (Hrsg.): Gravitation. Spektrum, 1996.
- (Hrsg.): Relativity theory and astrophysics. American Mathematical Society, 1967.
- (Hrsg.): Isolated gravitational systems in general relativity. E. Fermi School, Varenna 1977, North Holland 1979.
- Mit Claus Lämmerzahl (Hrsg.): Special relativity: will it survive the next 101 years ? Springer 2006 (Heraeus Seminar).
- Mit H. Friedrich (Hrsg.): Canonical gravity- from classical to quantum. Springer 1994 (Heraeus Seminar).
- Mit Peter Schneider, E. E. Falco: Gravitational Lenses. Springer 1992, 1999.
- Mit Wolfgang Kundt: Exact solutions of gravitational field equations. In: L. Witten (Hrsg.): Gravitation – introduction to current research. Wiley 1962-
- Survey of General Relativity. In: Werner Israel (Hrsg.): Relativity, Astrophysics and Cosmology. Reidel 1973.
- Beiträge zur relativistischen Dynamik kontinuierlicher Medien, Abhandlungen der Mathem.-Naturwiss. Klasse, Akademie der Wissenschaften Mainz, Nr. 11, 1961, S. 782–837, wieder abgedruckt in: George F. R. Ellis, Malcolm A. H. MacCallum, Andrzej Krasinski (Hrsg.) Golden Oldies in General Relativity. Hidden Gems, Springer Verlag 2013.
- Mit Pascual Jordan, Wolfgang Kundt Strenge Lösungen der Feldgleichungen der Allgemeinen Relativitätstheorie, Abhandlungen der Mathem.-Naturwiss. Klasse, Akademie der Wissenschaften Mainz, Nr. 2, 1960, S. 21–105.
- Mit Felix Pirani, Alfred Schild The geometry of free fall and light propagation, in O´Raifeartaigh (Hrsg.) General Relativity. Papers in honour of J. L. Synge, Oxford, Clarendon Press 1972, S. 63–84.
Literatur
- Bernd G. Schmidt (Hrsg.): Einstein’s field equations and their physical implications. Selected essays in honour of Jürgen Ehlers. Springer 2000.
Weblinks
- Literatur von und über Jürgen Ehlers im Katalog der Deutschen Nationalbibliothek
- Nachruf von Reinhard Breuer
- Nachruf beim Max-Planck-Institut
- Nachruf von Claus Lämmerzahl und Hermann Nikolai im Physik-Journal, PDF
Einzelnachweise
- ↑ George Ellis, Andrzej Krasiński: Editors' comment. In: General Relativity and Gravitation. Bd. 39, 2007, S. 1941–1942.
- ↑ Rüdiger Braun: Wo Zeit und Raum aufhören. Der Mitbegründer des Golmer Max-Planck-Instituts für Gravitationsphysik, Jürgen Ehlers, ist unerwartet verstorben. In: Märkische Allgemeine Zeitung. 27. Mai 2008.
- ↑ Bernd Schmidt: Vorwort. In: Einstein's Field Equations and their Physical Implications. Selected Essays in Honour of Jürgen Ehlers. Springer, Berlin 2000, ISBN 3-540-67073-4, S. 1–126.
| Personendaten | |
|---|---|
| NAME | Ehlers, Jürgen |
| KURZBESCHREIBUNG | deutscher Physiker |
| GEBURTSDATUM | 29. Dezember 1929 |
| GEBURTSORT | Hamburg |
| STERBEDATUM | 20. Mai 2008 |
| STERBEORT | Potsdam |