Phasenverschiebung: Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Elektrische Größe
- Schwingungslehre
imported>Saure (Änderung 167621653 von 188.99.205.196 rückgängig gemacht; die Angabe 90° für ideale Bauelemente gilt für jede Frequenz) |
imported>Diopuld (→Weblinks: DNB) |
||
| Zeile 1: | Zeile 1: | ||
Die '''Phasenverschiebung''', auch '''Phasendifferenz''' oder '''Phasenlage''', ist ein Begriff der Physik und Technik im Zusammenhang mit periodischen Vorgängen. Zwei [[Sinusschwingung | Die '''Phasenverschiebung''', auch '''Phasendifferenz''' oder '''Phasenlage''', ist ein Begriff der Physik und Technik im Zusammenhang mit periodischen Vorgängen. Zwei [[Sinusschwingung]]en sind gegeneinander in ihren [[Phasenwinkel]]n verschoben, wenn ihre [[Periodendauer]]n zwar übereinstimmen, die Zeitpunkte ihrer [[Nulldurchgang|Nulldurchgänge]] aber nicht. Die Angabe einer konstanten Phasenverschiebung ist auch dann möglich, wenn die Periodenlängen nicht gleich, aber ganzzahlige Vielfache voneinander sind. | ||
Phasenverschiebungen können dort auftreten, wo Zeitglieder, [[Trägheit]]en oder [[Blindwiderstand|Reaktanzen]] eine Rolle spielen, so vor allem in der [[Elektrotechnik]], der [[Elektroakustik]], der [[Akustik]] und in der [[Mechanik|Schwingungsmechanik]]. Der Begriff wird auch in anderen Gebieten angewendet, siehe [[#Andere Gebiete|unten]]. | Phasenverschiebungen können dort auftreten, wo Zeitglieder, [[Trägheit]]en oder [[Blindwiderstand|Reaktanzen]] eine Rolle spielen, so vor allem in der [[Elektrotechnik]], der [[Elektroakustik]], der [[Akustik]] und in der [[Mechanik|Schwingungsmechanik]]. Der Begriff wird auch in anderen Gebieten angewendet, siehe [[#Andere Gebiete|unten]]. | ||
[[Datei:Rot.-Zeiger2.svg|mini|upright=1.75|Rechts: Zwei Schwingungen, die | [[Datei:Rot.-Zeiger2.svg|mini|upright=1.75|Rechts: Zwei Schwingungen in ihrem Verlauf über dem Phasenwinkel <math>\omega t</math>, die gegeneinander um den Winkel <math>\Delta \varphi</math> verschoben sind.<br />Links: Zwei rotierende Zeiger mit demselben Unterschied im Phasenwinkel. Deren Projektionen auf die senkrechte [[Ursprungsgerade]] ergeben die Augenblickswerte.<br />Die blau gezeichnete Schwingung läuft der rot gezeichneten um 60° vor.]] | ||
== Veranschaulichung == | == Veranschaulichung == | ||
Eine Phasenverschiebung ist in einem [[Liniendiagramm]] der Wechselgrößen über der Zeit am Versatz der Nulldurchgänge (bei gleichem Vorzeichen der Anstiege der Kurven) zu sehen. Sie lässt sich auch im [[Zeigermodell]] veranschaulichen. Die zwei Schwingungen werden durch Zeiger symbolisiert, die beide um den Koordinatenursprung mit derselben konstanten [[Winkelgeschwindigkeit]] <math>\omega</math> rotieren. | Eine Phasenverschiebung ist in einem [[Liniendiagramm]] der Wechselgrößen über der Zeit am Versatz der Nulldurchgänge (bei gleichem Vorzeichen der Anstiege der Kurven) zu sehen. Sie lässt sich auch im [[Zeigermodell]] veranschaulichen. Die zwei Schwingungen werden durch Zeiger symbolisiert, die beide um den Koordinatenursprung mit derselben konstanten [[Winkelgeschwindigkeit]] <math>\omega</math> rotieren. Ein Zeiger <math>\underline z</math> ist dabei eine [[Komplexe Zahl|komplexe]] Größe <math>\underline z=x+\mathrm jy</math> mit dem [[Realteil]] <math>\mathrm {Re}\,\underline z = x</math> und dem [[Imaginärteil]] <math>\mathrm {Im}\,\underline z = y</math>. Die horizontale Auslenkung <math>x</math> und die vertikale Auslenkung <math>y</math> sind beide reell, siehe auch [[DIN 1302]]. | ||
Der Richtungssinn der Phasenverschiebung einer Schwingung gegenüber der Bezugsschwingung führt zu den Bezeichnungen ''Nacheilwinkel'' oder ''Voreilwinkel'', ferner Nacheilen oder Voreilen. Die Verwendung der Zeiger als komplexe Größen erleichtert vielfach mathematische Berechnungen (siehe [[komplexe Wechselstromrechnung]]). | Eine volle Umdrehung entspricht einer vollen Periode der Schwingung. Der '''Phasenverschiebungswinkel''',<ref name="DIN 11">DIN 1311-1:2000 ''Schwingungen und schwingungsfähige Systeme''.</ref><ref name="DIN 10">DIN 40 110-1:1994 ''Wechselstromgrößen – Zweileiter-Stromkreise''.</ref> auch als '''Phasendrehung''' bezeichnet, ist hier der von beiden Zeigern eingeschlossene Winkel. | ||
Der Richtungssinn der Phasenverschiebung einer Schwingung gegenüber der Bezugsschwingung führt zu den Bezeichnungen ''Nacheilwinkel'' oder ''Voreilwinkel'', ferner Nacheilen oder Voreilen. Die Verwendung der Zeiger als komplexe Größen erleichtert vielfach mathematische Berechnungen (siehe [[komplexe Wechselstromrechnung]]). | |||
== Größenangabe der Phasenverschiebung == | == Größenangabe der Phasenverschiebung == | ||
[[Datei:Typenschild-Doppelt gespeiste Asynchronmaschine Apel.jpg|mini|Motor-Typenschild mit Angabe des cos ''φ'' zur Kennzeichnung der Phasenverschiebung (rechts in mittlerer Höhe)]] | [[Datei:Typenschild-Doppelt gespeiste Asynchronmaschine Apel.jpg|mini|Motor-Typenschild mit Angabe des cos ''φ'' zur Kennzeichnung der Phasenverschiebung (rechts in mittlerer Höhe)]] | ||
Eine Periodendauer entspricht dem [[Vollwinkel]] von 360°, und die zeitliche Phasenverschiebung wird als Winkel <math>\Delta\varphi</math> angegeben. Statt <math>\Delta \varphi</math> wird auch einfach <math>\varphi</math> geschrieben, sofern Verwechslungen ausgeschlossen sind. Eindeutiger ist ein indiziertes Formelzeichen; beispielsweise kann bei einer Spannung <math>u=\hat u\,\ | Eine Periodendauer entspricht dem [[Vollwinkel]] von 360°, und die zeitliche Phasenverschiebung wird als Winkel <math>\Delta\varphi</math> angegeben. Statt <math>\Delta \varphi</math> wird auch einfach <math>\varphi</math> geschrieben, sofern Verwechslungen ausgeschlossen sind. Eindeutiger ist ein indiziertes Formelzeichen; beispielsweise kann bei einer Spannung <math>u=\hat u\,\sin(\omega t+ \varphi_u)</math> gegenüber einer Stromstärke <math>i=\hat \imath \,\sin(\omega t+ \varphi_i)</math> für die Differenz <math>\varphi_u -\varphi_i</math> ein erklärendes <math>\varphi_{ui}</math> verwendet werden. Dasselbe <math>\varphi_{ui}</math> ergibt sich bei der Schreibweise <math>u=\hat u\,\cos(\omega t+ \varphi_u)</math> zusammen mit <math>i=\hat \imath \,\cos(\omega t+ \varphi_i)</math>. | ||
Winkel werden in [[Radiant (Einheit)|Radiant]] oder in [[Grad (Winkel)|Grad]] angegeben;<ref name="DIN 01">DIN 1301-1:2010 ''Einheiten – Einheitennamen, Einheitenzeichen''.</ref> z. B. bedeuten die Angaben <math>\frac\pi 2</math> und 90° dieselbe Phasenverschiebung von einer Viertelperiode. Es ist auch möglich, als Maß die ''Phasenverschiebungszeit'' <math>\Delta t=\Delta \varphi/\omega</math> anzugeben<ref name="DIN 11" /> oder eine Längenangabe, wenn bei dem Vorgang ein räumlicher Weg zurückgelegt wird, z. B. bei einem Lichtstrahl. | Winkel werden in [[Radiant (Einheit)|Radiant]] oder in [[Grad (Winkel)|Grad]] angegeben;<ref name="DIN 01">DIN 1301-1:2010 ''Einheiten – Einheitennamen, Einheitenzeichen''.</ref> z. B. bedeuten die Angaben <math>\frac\pi 2</math> und 90° dieselbe Phasenverschiebung von einer Viertelperiode. Es ist auch möglich, als Maß die ''Phasenverschiebungszeit'' <math>\Delta t=\Delta \varphi/\omega</math> anzugeben<ref name="DIN 11" /> oder eine Längenangabe, wenn bei dem Vorgang ein räumlicher Weg zurückgelegt wird, z. B. bei einem Lichtstrahl. | ||
In der elektrischen Energietechnik wird die Phasenverschiebung durch den [[Kosinus]] des Phasenverschiebungswinkels <math>\varphi</math>, also <math>\cos\varphi</math>, angegeben. Der „<math>\cos\varphi</math>“, auch [[Wirkfaktor]] genannt, ist auf jedem Wechselstrommotor-Leistungsschild sowie anderen reaktiven elektrischen Verbrauchern angegeben und dient zum Beispiel zur Berechnung des [[Wirkleistung]]s-Anteils an der [[Scheinleistung|Gesamtleistung]] oder zur Bemessung von Schaltkontakten (vgl. [[Schaltlichtbogen]]). | In der elektrischen Energietechnik wird die Phasenverschiebung durch den [[Kosinus]] des Phasenverschiebungswinkels <math>\varphi</math>, also <math>\cos\varphi</math>, angegeben. Der „<math>\cos\varphi</math>“, auch [[Wirkfaktor]] genannt, ist auf jedem Wechselstrommotor-Leistungsschild sowie anderen reaktiven elektrischen Verbrauchern angegeben und dient zum Beispiel zur Berechnung des [[Wirkleistung]]s-Anteils an der [[Scheinleistung|Gesamtleistung]] oder zur Bemessung von Schaltkontakten (vgl. [[Schaltlichtbogen]]). (Die alleinige Angabe des <math>\cos\varphi</math> sagt aber noch nichts über die „Art“ bzw. [[Blindleistung#Bezeichnung der Orientierung bzw. Flussrichtung von Blindleistung|Flussrichtung der Blindleistung]] aus (ob induktiver oder kapazitiver Blindleistungs-Verbrauch), da bei der Bildung des <math>\cos</math> das Vorzeichen von <math>\varphi</math> verloren geht.) | ||
Mit einem [[Oszilloskop]] können zwei oder mehr gegeneinander zeitlich verschobene Schwingungen als einzelne Kurven unmittelbar in ihrem zeitlichen Verlauf sichtbar gemacht werden. Der zeitliche Versatz der Nulldurchgänge <math>\Delta t</math> und die Periodendauer <math>T</math> lassen sich ablesen und der Phasenverschiebungswinkel ausrechnen: | Mit einem [[Oszilloskop]] können zwei oder mehr gegeneinander zeitlich verschobene Schwingungen als einzelne Kurven unmittelbar in ihrem zeitlichen Verlauf sichtbar gemacht werden. Der zeitliche Versatz der Nulldurchgänge <math>\Delta t</math> und die Periodendauer <math>T</math> lassen sich ablesen und der Phasenverschiebungswinkel ausrechnen: | ||
| Zeile 83: | Zeile 85: | ||
In der [[Ökologie]] werden in [[Räuber-Beute-Beziehung]]en oft periodische [[Population (Biologie)|Populationsschwankungen]] beobachtet. Dabei erfolgt die Schwankung der [[Prädator|Räuber]]-Population gegenüber der [[Beutetier|Beute]]-Population phasenverzögert. (s. [[Lotka-Volterra-Regeln]]) | In der [[Ökologie]] werden in [[Räuber-Beute-Beziehung]]en oft periodische [[Population (Biologie)|Populationsschwankungen]] beobachtet. Dabei erfolgt die Schwankung der [[Prädator|Räuber]]-Population gegenüber der [[Beutetier|Beute]]-Population phasenverzögert. (s. [[Lotka-Volterra-Regeln]]) | ||
Bei einer [[Wärmedämmung]] wird mit Phasenverschiebung der Zeitraum zwischen dem Auftreten der höchsten Temperatur auf der Außenoberfläche eines Bauteils bis zum Erreichen der höchsten Temperatur auf dessen Innenfläche bezeichnet, obwohl keine sinusförmige Funktion vorliegt. | |||
== Mathematische Beschreibung == | == Mathematische Beschreibung == | ||
| Zeile 102: | Zeile 104: | ||
=== Phasenverschiebung um 180° und Phasenumkehr === | === Phasenverschiebung um 180° und Phasenumkehr === | ||
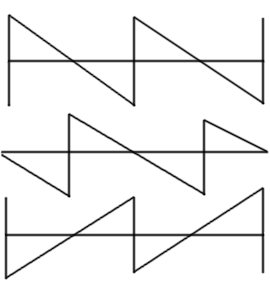
[[Bild:VerpoltesSignalA.png|mini|Sägezahnsignal als Beispiel für ein nicht symmetrisches Signal:<br />oben: Originalsignal<br />mitte: In der Grundschwingung um 180° phasenverschobenes Signal<br />unten: Verpoltes Signal]] | [[Bild:VerpoltesSignalA.png|mini|Sägezahnsignal als Beispiel für ein nicht symmetrisches Signal:<br />oben: Originalsignal<br />mitte: In der Grundschwingung um 180° phasenverschobenes Signal<br />unten: Verpoltes Signal]] | ||
Bei einer [[Phasenumkehr]] werden positive [[Augenblickswert]]e zu negativen, und negative zu positiven Augenblickswerten. Bei einem symmetrischen, beispielsweise sinusförmigen Wechselsignal erscheint eine Phasenumkehr wie eine Phasenverschiebung um 180° der Grundschwingung. Im Allgemeinen gibt es einen Zusammenhang zwischen | Bei einer [[Phasenumkehr]] werden positive [[Augenblickswert]]e zu negativen, und negative zu positiven Augenblickswerten. Bei einem symmetrischen, beispielsweise sinusförmigen Wechselsignal erscheint eine Phasenumkehr wie eine Phasenverschiebung um 180° der Grundschwingung. Im Allgemeinen gibt es einen Zusammenhang zwischen Phasenverschiebung und Phasenumkehr nicht. Eine sinusförmige Schwingung, welche gegenüber einer anderen sinusförmigen Schwingung gleicher Frequenz und Amplitude um 180° phasenverschoben ist, wird als „Gegenphase“ bezeichnet. | ||
== Weblinks == | == Weblinks == | ||
{{Wiktionary}} | {{Wiktionary}} | ||
*{{DNB-Portal|4200566-8}} | |||
*[http://www.sengpielaudio.com/LaufzeitdifferenzUndPhasenverschiebung.pdf Phasenverschiebung ''φ'' und Laufzeitdifferenz ''Δ t''] (PDF-Datei; 178 kB) | *[http://www.sengpielaudio.com/LaufzeitdifferenzUndPhasenverschiebung.pdf Phasenverschiebung ''φ'' und Laufzeitdifferenz ''Δ t''] (PDF-Datei; 178 kB) | ||
*[http://www.sengpielaudio.com/Rechner-LaufzeitPhase.htm Rechner: Zusammenhang von Phase, Phasenwinkel, Frequenz und Laufzeit (Delay)] | *[http://www.sengpielaudio.com/Rechner-LaufzeitPhase.htm Rechner: Zusammenhang von Phase, Phasenwinkel, Frequenz und Laufzeit (Delay)] | ||
*[http://www.sengpielaudio.com/VerpolungPhasenverschiebungVerschiedeneBegriffe.pdf Verpolung und Phasenverschiebung sind verschiedene Begriffe] (PDF; 62 kB) | *[http://www.sengpielaudio.com/VerpolungPhasenverschiebungVerschiedeneBegriffe.pdf Verpolung und Phasenverschiebung sind verschiedene Begriffe] (PDF; 62 kB) | ||
*[http://www.afug-info.de/Tipps-Tricks/Phasenverschiebung_Winkel/ Phasenwinkel φ berechnen - Die Phasenverschiebung als praktische Anwendung mit dem Oszilloskop] (www.Afug-Info.de) | |||
== Einzelnachweise == | == Einzelnachweise == | ||
<references /> | <references /> | ||
{{Normdaten|TYP=s|GND=4200566-8}} | |||
[[Kategorie:Elektrische Größe]] | [[Kategorie:Elektrische Größe]] | ||
Aktuelle Version vom 14. Februar 2022, 17:52 Uhr
Die Phasenverschiebung, auch Phasendifferenz oder Phasenlage, ist ein Begriff der Physik und Technik im Zusammenhang mit periodischen Vorgängen. Zwei Sinusschwingungen sind gegeneinander in ihren Phasenwinkeln verschoben, wenn ihre Periodendauern zwar übereinstimmen, die Zeitpunkte ihrer Nulldurchgänge aber nicht. Die Angabe einer konstanten Phasenverschiebung ist auch dann möglich, wenn die Periodenlängen nicht gleich, aber ganzzahlige Vielfache voneinander sind.
Phasenverschiebungen können dort auftreten, wo Zeitglieder, Trägheiten oder Reaktanzen eine Rolle spielen, so vor allem in der Elektrotechnik, der Elektroakustik, der Akustik und in der Schwingungsmechanik. Der Begriff wird auch in anderen Gebieten angewendet, siehe unten.
Links: Zwei rotierende Zeiger mit demselben Unterschied im Phasenwinkel. Deren Projektionen auf die senkrechte Ursprungsgerade ergeben die Augenblickswerte.
Die blau gezeichnete Schwingung läuft der rot gezeichneten um 60° vor.
Veranschaulichung
Eine Phasenverschiebung ist in einem Liniendiagramm der Wechselgrößen über der Zeit am Versatz der Nulldurchgänge (bei gleichem Vorzeichen der Anstiege der Kurven) zu sehen. Sie lässt sich auch im Zeigermodell veranschaulichen. Die zwei Schwingungen werden durch Zeiger symbolisiert, die beide um den Koordinatenursprung mit derselben konstanten Winkelgeschwindigkeit $ \omega $ rotieren. Ein Zeiger $ {\underline {z}} $ ist dabei eine komplexe Größe $ {\underline {z}}=x+\mathrm {j} y $ mit dem Realteil $ \mathrm {Re} \,{\underline {z}}=x $ und dem Imaginärteil $ \mathrm {Im} \,{\underline {z}}=y $. Die horizontale Auslenkung $ x $ und die vertikale Auslenkung $ y $ sind beide reell, siehe auch DIN 1302.
Eine volle Umdrehung entspricht einer vollen Periode der Schwingung. Der Phasenverschiebungswinkel,[1][2] auch als Phasendrehung bezeichnet, ist hier der von beiden Zeigern eingeschlossene Winkel.
Der Richtungssinn der Phasenverschiebung einer Schwingung gegenüber der Bezugsschwingung führt zu den Bezeichnungen Nacheilwinkel oder Voreilwinkel, ferner Nacheilen oder Voreilen. Die Verwendung der Zeiger als komplexe Größen erleichtert vielfach mathematische Berechnungen (siehe komplexe Wechselstromrechnung).
Größenangabe der Phasenverschiebung
Eine Periodendauer entspricht dem Vollwinkel von 360°, und die zeitliche Phasenverschiebung wird als Winkel $ \Delta \varphi $ angegeben. Statt $ \Delta \varphi $ wird auch einfach $ \varphi $ geschrieben, sofern Verwechslungen ausgeschlossen sind. Eindeutiger ist ein indiziertes Formelzeichen; beispielsweise kann bei einer Spannung $ u={\hat {u}}\,\sin(\omega t+\varphi _{u}) $ gegenüber einer Stromstärke $ i={\hat {\imath }}\,\sin(\omega t+\varphi _{i}) $ für die Differenz $ \varphi _{u}-\varphi _{i} $ ein erklärendes $ \varphi _{ui} $ verwendet werden. Dasselbe $ \varphi _{ui} $ ergibt sich bei der Schreibweise $ u={\hat {u}}\,\cos(\omega t+\varphi _{u}) $ zusammen mit $ i={\hat {\imath }}\,\cos(\omega t+\varphi _{i}) $.
Winkel werden in Radiant oder in Grad angegeben;[3] z. B. bedeuten die Angaben $ {\frac {\pi }{2}} $ und 90° dieselbe Phasenverschiebung von einer Viertelperiode. Es ist auch möglich, als Maß die Phasenverschiebungszeit $ \Delta t=\Delta \varphi /\omega $ anzugeben[1] oder eine Längenangabe, wenn bei dem Vorgang ein räumlicher Weg zurückgelegt wird, z. B. bei einem Lichtstrahl.
In der elektrischen Energietechnik wird die Phasenverschiebung durch den Kosinus des Phasenverschiebungswinkels $ \varphi $, also $ \cos \varphi $, angegeben. Der „$ \cos \varphi $“, auch Wirkfaktor genannt, ist auf jedem Wechselstrommotor-Leistungsschild sowie anderen reaktiven elektrischen Verbrauchern angegeben und dient zum Beispiel zur Berechnung des Wirkleistungs-Anteils an der Gesamtleistung oder zur Bemessung von Schaltkontakten (vgl. Schaltlichtbogen). (Die alleinige Angabe des $ \cos \varphi $ sagt aber noch nichts über die „Art“ bzw. Flussrichtung der Blindleistung aus (ob induktiver oder kapazitiver Blindleistungs-Verbrauch), da bei der Bildung des $ \cos $ das Vorzeichen von $ \varphi $ verloren geht.)
Mit einem Oszilloskop können zwei oder mehr gegeneinander zeitlich verschobene Schwingungen als einzelne Kurven unmittelbar in ihrem zeitlichen Verlauf sichtbar gemacht werden. Der zeitliche Versatz der Nulldurchgänge $ \Delta t $ und die Periodendauer $ T $ lassen sich ablesen und der Phasenverschiebungswinkel ausrechnen:
- $ {\frac {\Delta \varphi }{360^{\circ }}}={\frac {\Delta t}{T}}\;. $
Stimmen die Phasenwinkel überein, ist also die Phasendifferenz null, so werden die Schwingungen als „gleichphasig“ oder „phasengleich“ bezeichnet; umgangssprachlich liegen sie „in Phase“.
Erscheinungsformen, Anwendungen
Elektrotechnik
Phasenverschiebung zwischen Strom und Spannung an einer Induktivität |
Phasenverschiebung zwischen Strom und Spannung an einer Kapazität |
In der Elektrotechnik wird der Begriff Phasenverschiebung in einem Wechselstromkreis im Zusammenhang mit Stromstärken und Spannungen verwendet. Eine Verschiebung tritt immer dann auf, wenn ein mit Wechselstrom betriebener Zweitor induktive oder kapazitive, differenzierende oder verzögernde Eigenschaften besitzt. Im Bereich hoher Frequenzen kann dafür allein schon die Signallaufzeit verantwortlich sein.
- Bei einer Induktivität (ideale Spule) folgt die Stromstärke der Spannung um 90° nach (die Spannung eilt der Stromstärke um 90° vor). Der Phasenverschiebungswinkel $ \Delta \varphi =\varphi _{ui} $ wird positiv angegeben; er ist unabhängig von der Frequenz.
- Bei einer Kapazität (idealer Kondensator) folgt die Spannung der Stromstärke um 90° nach. Der Phasenverschiebungswinkel wird negativ angegeben; er ist unabhängig von der Frequenz.
- Beim ohmschen Widerstand sind Spannung und Stromstärke immer gleichphasig.
- Bei einer Kombination von R, L und C kann der Phasenverschiebungswinkel beliebige Werte zwischen −90° und +90° annehmen; er hängt von der Frequenz ab und ändert sich besonders stark in der Nähe einer Resonanzstelle; vergleiche: Schwingkreis.
Hochfrequenztechnik
Hier wird die Phasenverschiebung zur Phasenmodulation verwendet. Im zweiseitigen Frequenzspektrum bedeutet das, dass der Zeiger der Signalfrequenz in wechselnde Richtungen in Bezug auf den Zeiger der Trägerfrequenz zeigt. Damit können Daten kodiert werden.
Akustik, Tontechnik
Werden zwei oder mehrere Schallwellen gleicher Frequenz überlagert, so resultiert je nach Phasenverschiebungswinkel ein entweder verstärktes oder gedämpftes Signal. Eine solche Überlagerung wird Interferenz genannt und ist im Schallfeld ortsabhängig: Je nach Abstand und Position der Quellen ergeben sich an unterschiedlichen Betrachterpositionen alle möglichen Kombinationen von Verstärkungen und Abschwächungen (zum Thema Abschwächungen siehe auch Antischall).
| $ \Delta \varphi $ | $ \Delta \varphi $ | $ f $ | $ \lambda $ |
|---|---|---|---|
| 360° | 2 π rad | 2000 Hz | 0,1715 m |
| 180° | π rad | 1000 Hz | 0,3430 m |
| 90° | π/2 rad | 500 Hz | 0,6860 m |
| 45° | π/4 rad | 250 Hz | 1,372 m |
| 22,5° | π/8 rad | 125 Hz | 2,744 m |
| 11,25° | π/16 rad | 62,5 Hz | 5,488 m |
Mit der Festlegung der Einheiten für den ebenen Winkel[3]
- $ 1\ \mathrm {rad} =1\ {\frac {\mathrm {m} }{\mathrm {m} }}=1\;;\quad 1^{\circ }=(\pi /180)\ \mathrm {rad} $,
mit der Wellenlänge $ \lambda =c/f $ und der Schallgeschwindigkeit $ c $ = 343 m/s bei 20 °C
ergeben sich beispielsweise für eine feste Verzögerung von $ \Delta t $ = 0,5 ms nebenstehende frequenzabhängige Phasenverschiebungswinkel $ \Delta \varphi $:
Die Einheit Radiant kann weggelassen werden, wenn sie nicht zur Verdeutlichung einer Winkelangabe dienen soll.
Zum akustischen Zusammenhang von Phasenverschiebung $ \Delta \varphi $ und Laufzeitdifferenz bei Stereofonie, $ \Delta t $ siehe Laufzeitstereofonie. Mit digitaler Signalverarbeitung ist es heute möglich, die Phasenlage mehreren Lautsprechern zugeführter Signale individuell zu verstellen und damit für einen kleinen Abhörpunkt oder Messpunkt das Schallfeld gezielt zu steuern.
Andere Gebiete
In der Optik werden Linsen entspiegelt, indem eine dünne Schicht auf der Glasoberfläche eine Doppelreflexion erzeugt, die bei einer bestimmten Wellenlänge λ eine Phasenverschiebung der beiden Reflexionen von ½ λ erreicht. Üblicherweise wird die Schichtdicke auf die Wellenlänge des gelben Lichts (λ ≈ 600 nm) eingestellt.
Auch in den Wirtschaftswissenschaften sind Phasenverschiebungen bekannt, wie z. B. beim Schweinezyklus. Zeitverzögerungen im Regelmechanismus zwischen Nachfrage, Angebot und resultierendem Preis sowie den sich daraus ableitenden Investitionsanreizen erläutern das Phänomen einer Phasenverschiebung zwischen Preis und Güterstrom.
In der Ökologie werden in Räuber-Beute-Beziehungen oft periodische Populationsschwankungen beobachtet. Dabei erfolgt die Schwankung der Räuber-Population gegenüber der Beute-Population phasenverzögert. (s. Lotka-Volterra-Regeln)
Bei einer Wärmedämmung wird mit Phasenverschiebung der Zeitraum zwischen dem Auftreten der höchsten Temperatur auf der Außenoberfläche eines Bauteils bis zum Erreichen der höchsten Temperatur auf dessen Innenfläche bezeichnet, obwohl keine sinusförmige Funktion vorliegt.
Mathematische Beschreibung
Gleichungen für Schwingung und rotierenden Zeiger
Der einfachste Fall einer Schwingung ist die harmonische Schwingung. Mathematisch lässt sie sich beschreiben durch
- $ x(t)={\hat {x}}\cdot \cos(\omega \cdot t+\varphi _{0})\;;\quad {\underline {x}}(t)={\hat {x}}\cdot \mathrm {e} ^{\mathrm {j} (\omega \cdot t+\varphi _{0})} $
wobei $ x(t) $ der reelle Wert zur Zeit $ t $, $ {\underline {x}}(t) $ der komplexe Wert, $ {\hat {x}} $ die Amplitude, $ \omega =2\pi f $ die Kreisfrequenz, $ f $ die Frequenz und $ \mathrm {j} $ die imaginäre Einheit darstellen. $ \varphi (t)=\omega \,t+\varphi _{0} $ wird als Phasenwinkel bezeichnet und $ \varphi _{0} $ als Nullphasenwinkel.[1][2]
Phasenverschiebungswinkel und Phasenlaufzeit
Der Zusammenhang zwischen dem Phasenverschiebungswinkel $ \Delta \varphi $ und der Laufzeitdifferenz $ \Delta t $ ist:
- $ \Delta \varphi =\omega \cdot \Delta t=2\pi \cdot f\cdot \Delta t $
oder umgestellt
- $ \Delta t={\frac {\Delta \varphi }{\omega }}={\frac {\Delta \varphi }{2\pi \,f}}={\frac {\Delta \varphi }{360^{\circ }\,f}} $
aufgrund der oben angegebenen Umrechnungen
- $ \omega =2\pi f\ $ und $ 2\pi =360^{\circ } $ .
Phasenverschiebung um 180° und Phasenumkehr
Bei einer Phasenumkehr werden positive Augenblickswerte zu negativen, und negative zu positiven Augenblickswerten. Bei einem symmetrischen, beispielsweise sinusförmigen Wechselsignal erscheint eine Phasenumkehr wie eine Phasenverschiebung um 180° der Grundschwingung. Im Allgemeinen gibt es einen Zusammenhang zwischen Phasenverschiebung und Phasenumkehr nicht. Eine sinusförmige Schwingung, welche gegenüber einer anderen sinusförmigen Schwingung gleicher Frequenz und Amplitude um 180° phasenverschoben ist, wird als „Gegenphase“ bezeichnet.
Weblinks
- Literatur von und über Phasenverschiebung im Katalog der Deutschen Nationalbibliothek
- Phasenverschiebung φ und Laufzeitdifferenz Δ t (PDF-Datei; 178 kB)
- Rechner: Zusammenhang von Phase, Phasenwinkel, Frequenz und Laufzeit (Delay)
- Verpolung und Phasenverschiebung sind verschiedene Begriffe (PDF; 62 kB)
- Phasenwinkel φ berechnen - Die Phasenverschiebung als praktische Anwendung mit dem Oszilloskop (www.Afug-Info.de)
Einzelnachweise
pl:Kąt fazowy