Grenzschichtgleichungen

Ausbildung einer laminaren Grenzschicht an einer flachen Oberfläche (untere Linie)

Die Grenzschichtgleichungen treten in der Grenzschichttheorie als Vereinfachungen der Navier-Stokes-Gleichungen auf. Für eine zweidimensionale stationäre Strömung mit konstanter Dichte $ \rho $ lauten sie:

$ {\begin{aligned}u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}&=-{\frac {1}{\rho }}{\frac {\partial p}{\partial x}}+\nu {\frac {\partial ^{2}u}{\partial y^{2}}}\\{\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}&=0\\0&={\frac {\partial p}{\partial y}}\end{aligned}} $

mit

• $ x $: Koordinate in Strömungsrichtung
• $ y $: Koordinate senkrecht zur Strömungsrichtung (Wandabstand)
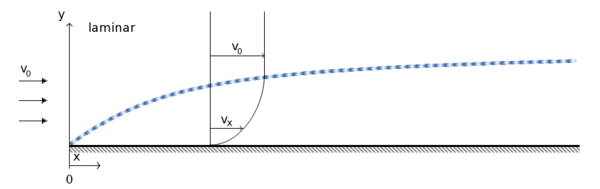
• $ u={\frac {dx}{dt}} $: Geschwindigkeitskomponente in Strömungsrichtung ($ v_{x} $ in der Abb.)
• $ v={\frac {dy}{dt}} $: Geschwindigkeitskomponente senkrecht zur Strömungsrichtung
• $ p $ der Druck
• $ \nu $ die kinematische Viskosität
• $ {\frac {\partial }{\partial }} $ die partielle Ableitung.

Die zweite Gleichung ist die Kontinuitätsgleichung für inkompressible Strömungen.

Die dritte Gleichung besagt, dass sich der Druck über die betrachtete Höhe nicht ändert, d. h. der Druck an der Körperoberfläche entspricht dem Druck in der reibungsfreien Außenströmung.

Druckgradient und Außenströmung

In der Außenströmung $ \left({\tfrac {\partial u}{\partial y}}=0\right) $ gilt die Eulergleichung:

$ \Rightarrow u_{\delta }{\frac {\partial u_{\delta }}{\partial x}}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial x}} $

mit

• $ u_{\delta } $: Geschwindigkeit der Außenströmung.

Sie besagt: der Druckgradient, d. h. der Verlauf des Druckes in Strömungsrichtung, ist

• negativ bei beschleunigter Strömung $ \left({\frac {\partial p}{\partial x}}<0\quad \Rightarrow \quad {\frac {\partial u_{\delta }}{\partial x}}>0\right) $
• Null bei einer Plattenströmung
• positiv bei verzögerter Strömung.

Anfangs- und Randbedingungen

Zur Berechnung der Geschwindigkeitsverteilung sind folgende Anfangs- und Randbedingungen erforderlich:

$ {\begin{aligned}u(x,y=0)&=0\\v(x,y=0)&=0\\u(x,y\rightarrow \infty )&=u_{\infty }(x)\end{aligned}} $

Die ersten beiden Gleichungen beschreiben die Haftbedingung an der Körperoberfläche, als dritte Bedingung ist die Geschwindigkeit der Außenströmung vorgegeben ($ \delta $ ist die Dicke der Grenzschicht).

Aus der Haftbedingung lässt sich folgende Gleichung ableiten:

$ \Rightarrow \eta \left({\frac {\partial ^{2}u}{\partial y^{2}}}\right)_{y=0}={\frac {\mathrm {d} \,p(x)}{\mathrm {d} \,x}}, $

welche die Krümmung des Geschwindigkeitsprofils an der Wand mit dem durch die Außenströmung aufgeprägten Druckgradienten in Beziehung setzt ($ \eta =\rho \cdot \nu $ ist die dynamische Viskosität).

Eine Grenzschichtablösung kann nur bei verzögerter Außenströmung, d.h. bei positivem Druckgradienten, auftreten. Die Grenzschicht löst von der Körperkontur ab, wenn die Wandschubspannung verschwindet:

$ \tau _{\text{wand}}=\eta \left({\frac {\partial u}{\partial y}}\right)_{y=0}=0. $

Lösung

Im Gegensatz zu den elliptischen Navier-Stokes-Gleichungen bilden die Grenzschichtgleichungen ein parabolisches Gleichungssystem. Dadurch gibt es keinen stromaufwärts gerichteten Informationsfluss, so dass eine numerische Lösung mit einem Upstream-Verfahren möglich ist.

Eine analytische Lösung der Grenzschichtgleichungen ist nur in einigen Sonderfällen möglich. Die einfachste Lösung ist die Grenzschichtströmung entlang einer unendlich dünnen, ebenen Platte (Blasius-Lösung). In diesem Fall sind die Lösungen an verschiedenen Stellen entlang der Platte ähnlich und können durch eine geeignete Skalierung der Koordinate normal zur Wand ineinander überführt werden. Dies liefert einen Ausdruck für die Grenzschichtdicke:

$ {\frac {\delta (x)}{x}}={\frac {5}{\sqrt {\mathrm {Re} _{x}}}}, $

mit der Reynoldszahl $ \mathrm {Re} _{x}={\frac {u_{\infty }\cdot x}{\nu }}. $

Als Dicke $ \delta (x) $ der Grenzschicht wird die Dicke festgelegt, bei der die Geschwindigkeit 99 % der Geschwindigkeit der freien Außenströmung erreicht hat:

$ u_{\delta }=u(y=\delta ):=0{,}99\cdot u_{\infty }\approx u_{\infty } $

Neben dieser Definition der Grenzschichtdicke wird als physikalisch sinnvolleres Maß oft die Verdrängungsdicke $ \delta _{1} $ oder die Impulsverlustdicke $ \delta _{2} $ verwendet.

Quellen

• Hermann Schlichting (et al.): Grenzschicht-Theorie. Springer, Berlin 2006, ISBN 3-540-23004-1

Literatur

• Spurk, Aksel: Strömungslehre, Springer, Berlin 2007, ISBN 978-3540384397