Drehkristallmethode
- Wikipedia:Vorlagenfehler/Vorlage:Literatur/Interner Fehler
- Kristallographie
Die Drehkristallmethode ist ein Röntgenbeugungsverfahren in der Kristallographie und eine Filmmethode, mit der man mittels monochromatischer Röntgenstrahlung die Gitterkonstanten eines Einkristalls bestimmen kann.
Die Drehkristallmethode ist die älteste Filmmethode und diente als Grundlage für die leistungsfähigeren Röntgenbeugungsmethoden. Sie wird heute in der Praxis kaum mehr verwendet.
Aufbau
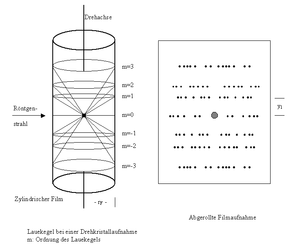
Ein Einkristall wird auf einem Goniometer so justiert, dass der Kristall um eine Achse des Kristallgitters gedreht werden kann. Um den Kristall wird ein zylinderförmig gerollter, röntgenempfindlicher Film so gelegt, dass die Zylinderachse und die Drehachse des Kristalls übereinstimmen. Zur Messung wird der Kristall senkrecht zur Drehachse mit einem monochromatischen Röntgenstrahl bestrahlt und dabei ausschließlich um diese Drehachse gedreht.
Messprinzip
Diese Messung lässt sich am besten mit Hilfe der Ewaldkugel darstellen. Dazu nimmt man an, dass die Drehachse in der kristallographischen c-Richtung liegt. Das bedeutet, dass die reziproken Gitterebenen vom Typ (h,k,m) (m=..-3;-2;-1;0;1;2;3 ...) senkrecht zu dieser Achse stehen. Dreht man den Kristall um die c-Achse, so schneiden diese Ebenen die Ewaldkugel in einem Kreis. Die vom Kristall gebeugten Strahlen liegen somit auf einem Kegel, dem Lauekegel, dessen Achse in Richtung der Drehachse liegt. Auf dem Film bilden diese Reflexe daher eine Linie. Der Öffnungswinkel der Kegel für die jeweiligen Ebenen hängt – außer von der Wellenlänge λ der verwendeten Strahlung – nur noch ab von der Gitterkonstanten in c-Richtung. Aus dem Abstand ym der zum m.ten Lauekegel gehörenden Linie von der Linie m=0 kann man daher die Gitterkonstante bestimmen:
- $ c={\frac {m\lambda }{\sin \arctan {\frac {y_{\mathrm {m} }}{r_{\mathrm {F} }}}}} $
wobei rF der Radius des vom Film gebildeten Zylinders ist.
Die Anwendung der Drehkristallmethode setzt nicht voraus, dass die gemessene Kristallrichtung die Richtung einer Gitterachse ist. Mit diesem Verfahren lässt sich für jeden Punkt des Kristallgitters die dazugehörige Länge des Gittervektors bestimmen.
Nachteile
Die Symmetrie der Abbildung ist immer mm2 (rhombisch-pyramidal) (siehe dazu auch Hermann-Mauguin-Symbolik). Daher kann man aus dem Film keine Rückschlüsse auf die tatsächliche Symmetrie des Kristalls ziehen.
Die Reflexe auf dem Film erscheinen nicht in einer bestimmten Reihenfolge. Infolgedessen ist es nicht möglich, einen Zusammenhang zwischen der Stellung des Kristalls und einem einzelnen Reflex herzustellen. Daher kann man die einzelnen Reflexe nicht eindeutig indizieren. Mit dieser Methode lassen sich daher nur Informationen über die Metrik des Kristallgitters gewinnen, aber keine Informationen über die Struktur des Kristalls.
Um dieses Problem zu verringern, wurde die Schwenkmethode entwickelt. Dabei wird der Kristall nicht vollständig um seine Achse gedreht, sondern nur noch um 5°-15° geschwenkt. Dieser Ansatz wurde aber durch leistungsfähigere Messmethoden wie das Weissenberg-Verfahren überholt.
Geschichte
Die Drehkristallmethode wurde 1913 erstmals von Maurice de Broglie genutzt.[1][2][3] Dabei benutzte er den Aufbau als Kristallspektrometer zur Untersuchung der Strahlung einer Röhre. Die Beobachtung beschränkte sich dabei auf die m=0-Linie. Bei vergleichbaren Untersuchungen wurden zusätzliche Reflexe entdeckt, die aber zuerst als Störung behandelt wurden.
Hugo Seemann setzte das Verfahren 1919 erstmals zur Untersuchung von Kristallstrukturen ein.[4]
Michael Polanyi, Ernst Schiebold und Karl Weissenberg entwickelten in den 1920er Jahren das Verfahren weiter und setzten es systematisch zur Strukturbestimmung von Kristallen ein.[5]
Auf Karl Weissenberg geht auch eine wesentliche Weiterentwicklung zurück, das Weissenberg-Verfahren. Damit ist es möglich, die einzelne Reflexe zu indizieren und deren Intensität zu bestimmen.
Das 1913 von W. H. und W. L. Bragg entwickelte Braggsche Spektrometer[6] unterschied sich von de Broglies Spektrometer nur darin, dass die Braggs eine bewegliche Ionisationskammer anstelle einer Photoplatte verwendeten. Auch die Braggs setzten ihr Verfahren zunächst zur Messung von Röntgenspektren ein, dann aber auch zur Bestimmung zahlreicher einfacher Kristallstrukturen, wofür sie 1915 den Nobelpreis für Physik erhielten.
Literatur
- Martin J. Buerger: Kristallographie. Walter de Gruyter, Berlin, 1977, ISBN 3-11-004286-X.
- Max von Laue: Röntgenstrahl-Interferenzen. 3. Auflage. Frankfurt am Main 1960.
Weblinks
- Simulation von Drehkristall- und Weissenberg-Aufnahmen
- Erklärung der Drehkristallmethode. IUCr teaching pamphlet. (eng.)
Einzelnachweise
- ↑ Maurice de Broglie: Sur un nouveau procédé permettant d'obtenir la photographie des spectres de raies des rayons de Röntgen. In: Comptes rendus de l’Académie des Sciences. Band 157, S. 924–926, (online).
- ↑ Maurice de Broglie: Enregistrement photographique continu des spectres des rayons de Röntgen; spectre du tungstène. Influence de l'agitation thermique. In: Comptes rendus de l’Académie des Sciences. Band 157, S. 1413–1416, (online).
- ↑ Maurice de Broglie: Sur la spectroscopie des rayons de Röntgen. In: Comptes rendus de l’Académie des Sciences. Band 158, S. 177–180, (online).
- ↑ Hugo Seemann: In: Physikalische Zeitschrift. Band 20, 1919, S. 169–175.
- ↑ Michael Polanyi, Ernst Schiebold, Karl Weissenberg: Über die Entwicklung des Drehkristallverfahrens. In: Zeitschrift für Physik. Band 23, Nummer 1, S. 337–340, doi:10.1007/BF01327599.
- ↑ W. H. Bragg, W. L. Bragg: The Reflection of X-rays by Crystals. Proc. R. Soc. Lond. A 88 (1913) S. 428–438 (online)