Fadenstrahlrohr
Ein Fadenstrahlrohr ist ein physikalischer Versuchsaufbau, bei dem sich beschleunigte Elektronen in einer Kugel aufgrund der Lorentzkraft, die ins Kugelinnere gerichtet ist, auf einer Kreisbahn bewegen. Beim Zusammenstoßen mit Gasmolekülen entsteht Licht, welches die Kreisbahn der Elektronen sichtbar macht.
Versuchsaufbau
In einen evakuierten Glaskolben wird etwas Gas (z. B. Wasserstoff oder Argon) gefüllt, so dass im Kolben ein niedriger Druck (ca. 0,1–1 Pa) herrscht. Dieser ist so bemessen, dass die Elektronen durch Zusammenstöße möglichst wenig abgebremst werden (Änderung der kinetischen Energie), die Zahl der Zusammenstöße aber zu einem sichtbaren Leuchten ausreicht.
Im Kolben befindet sich eine Elektronenkanone. Diese besteht aus einer Heizspirale, einer Kathode und einer Lochanode. Aus der Kathode treten Elektronen aus, die zur positiv geladenen Anode hin beschleunigt werden. Die meisten Elektronen werden an der Anode wieder absorbiert, aber durch ein Loch in der Anode verlässt ein kleiner Teil der Elektronen das Strahlerzeugungssystem. An die Helmholtz-Spulen wird außerdem noch ein Amperemeter angeschlossen um den Spulenstrom zu bestimmen. An die Elektronenkanone wird ein Voltmeter angeschlossen um die Beschleunigungsspannung anzupassen.
Ergebnis
Beim Einschalten der Heizspannung erhitzt sich die Heizspirale und Elektronen treten aus ihr heraus. In dem elektrischen Feld zwischen Anode und Kathode wirkt das elektrische Feld auf die Elektronen, das diese auf eine hohe Geschwindigkeit beschleunigt, sodass ein Teil der Elektronen durch eine kleine Öffnung in der Anode diese als Elektronenstrahl verlassen. Da der Spulenstrom nicht eingeschaltet ist, wirkt keine Kraft auf den Strahl und er behält seine Richtung bei. Wird nun aber der Spulenstrom zusätzlich eingeschaltet, lenkt die als Zentripetalkraft wirkende Lorentzkraft die Elektronen auf eine Kreisbahn.
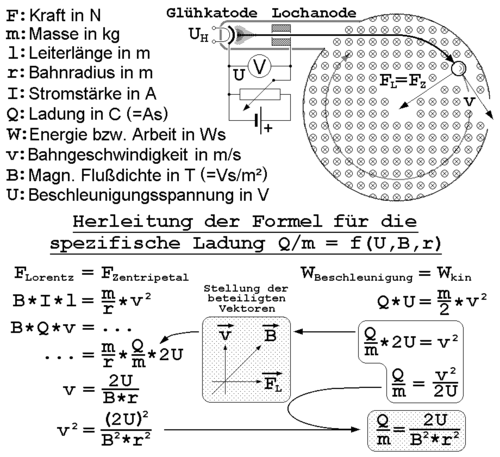
Bestimmung der spezifischen Ladung des Elektrons
Je höher der Spulenstrom ist, desto kleiner wird der Radius der Kreisbahn, da das Magnetfeld stärker wird. Die Stärke des Magnetfeldes und die Lorentzkraft sind zueinander proportional, so dass auch die Lorentzkraft zunimmt. Eine größere Lorentzkraft lenkt die Elektronen stärker ab, weshalb die Kreisbahn kleiner wird.
Die Lorentzkraft $ F_{L} $ steht immer zur augenblicklichen Bewegungsrichtung senkrecht und ermöglicht als Zentripetalkraft $ F_{Z} $ die Kreisbewegung. Den Betrag der Geschwindigkeit und folglich die Bewegungsenergie kann sie nicht ändern:
- $ {\begin{aligned}F_{L}&=F_{Z}\\e\cdot v\cdot B&=m\cdot {\frac {v^{2}}{r}}\end{aligned}} $
Daraus erhält man für den Betrag der spezifischen Elektronenladung
- $ {\frac {e}{m}}={\frac {v}{B\cdot r}} $
Die Bestimmung der Geschwindigkeit erfolgt mit Hilfe des Energieerhaltungssatzes
- $ e\cdot U={\frac {1}{2}}\cdot m\cdot v^{2} $
Damit folgt schließlich
- $ {\frac {e}{m}}={\frac {2\,U}{r^{2}\cdot B^{2}}} $
Die spezifische Elektronenladung hat den Wert
- $ {\frac {-e}{m}}\approx -1{,}7588202\cdot 10^{11}\,\mathrm {\frac {C}{kg}} $
Da die Ladung eines Elektrons aus dem Millikan-Versuch zugänglich ist, dient das Studium der Elektronen im Magnetfeld der Bestimmung ihrer Masse gemäß:
- $ \ m={\frac {e\cdot r^{2}\cdot B^{2}}{2\,U}}\approx 9{,}1094\cdot 10^{-31}\,\mathrm {kg} $
Ähnliche Konzepte für die Wägung von geladenen Teilchen findet man beim Massenspektrometer.
Dabei besitzt es seine Gültigkeit bei folgenden Bedingungen:
- Das magnetische Feld ist homogen
- Die Elektronen haben beim Austritt aus der Kathode die Geschwindigkeit Null
- $ {\vec {v}} $ $ \perp $ $ {\vec {B}} $
Weblinks
- Fadenstrahlrohr (LEIFI-Physik)