Geosynchrone Umlaufbahn

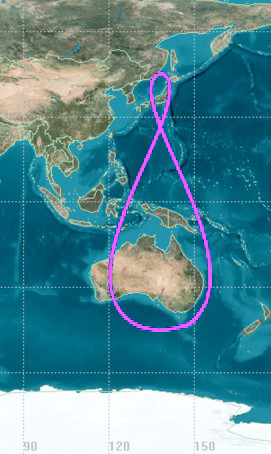
Eine geosynchrone Umlaufbahn ist ein Satellitenorbit, bei dem die Umlaufzeit um die Erde mit der Rotationsdauer der Erde (siderischer Tag) exakt übereinstimmt; der Satellit umkreist also die Erde zwar insgesamt synchron zur Erddrehung, jedoch nicht unbedingt synchron zu jedem Zeitpunkt. Da die Synchronizität nicht unbedingt für jeden Zeitpunkt des Umlaufs gilt, kann für einen Beobachter auf der Erdoberfläche der Satellit mit Exzentrizitäten ≠ 0 zeitweise seitlich vor- oder nachlaufen und für Bahnneigungen ≠ 0° auf- oder absteigen. Im speziellen Fall der geostationären Umlaufbahn (Bahnneigung = 0° und Exzentrizität = 0) steht ein Satellit für den Beobachter hingegen immer am selben Punkt am Himmel.
Da Vor- und Nachlauf und Auf- und Abbewegung sehr empfindlich auf Störungen der Bahnneigung und Exzentrizität reagieren, fallen Bahnstörungen hervorgerufen durch gravitative Einflüsse von Sonne und Mond und durch die Anisotropie des Gravitationsfeldes der Erde bei geosynchronen Umlaufbahnen besonders auf. Dort positionierte Satelliten benötigen Treibstoff, um die Bahnstörungen zu korrigieren. Allein dadurch haben sie nur eine begrenzte Lebensdauer.
Einsatzzwecke geostationärer Satelliten liegen hauptsächlich im Bereich der Kommunikation, aber auch Wettersatelliten nutzen die Vorteile dieses Orbits.
Orbitklassen
Geosynchrone Umlaufbahnen besitzen Inklinationswinkel von 0° (geostationär) über 90° (Polarbahn) bis 180° (retrograd, d. h. Gegenläufigkeit zur Erddrehung).
Geneigte Umlaufbahn
Ist die Inklination von 0° verschieden, so heißt die Umlaufbahn geneigter geosynchroner Orbit, englisch inclined geosynchronous orbit (IGSO).
Je nach Bahnneigung beziehungsweise Inklinationswinkel unterscheidet man:
- Umlaufbahnen mit geringer Bahnneigung werden unter dem Namen Inclined Orbit von vormaligen geostationären Nachrichtensatelliten benutzt, um ihre Lebensdauer bei fast erschöpften Treibstoffreserven zu verlängern. Weil ihre Position am Himmel dann jedoch schwankt, sind solche Satelliten nur noch mit professionellen Antennen mit Antennennachführung empfangbar.
- Das Quasi-Zenit-Satelliten-System (QZSS) bezeichnet ein System aus vier Satelliten, das für die Verbesserung der Satellitennavigationssysteme in Japan verwendet wird. Dabei stehen die Satelliten auf einer um 45° geneigten Bahn mit einer Exzentrizität von 0,09 und einem Perigäumswinkel (Argument des Perigäums) von 270° jeweils acht Stunden lang fast senkrecht über der Insel.
- Hochelliptische Orbits großer Inklination heißen auch Tundra-Orbits.
Geostationäre Umlaufbahn
Der Sonderfall einer kreisförmigen Umlaufbahn mit Drehrichtung Osten und einer Bahnneigung von 0° heißt geostationär. Die Bahngeschwindigkeit ist dabei stets 3.075 Meter pro Sekunde (11.070 km/h), und der Bahnradius beträgt 42.164 km. Nach Abzug des Äquatorradius von etwa 6.378 km entspricht dies einem Abstand von etwa 35.786 km zur Erdoberfläche.
Von der Erde aus betrachtet scheint ein geostationärer Satellit am Himmel still zu stehen (er ist „stationär“), da er sich mit derselben Winkelgeschwindigkeit bewegt wie der Beobachter auf der Erde. Deswegen wird diese Umlaufbahn häufig für Fernseh- und Kommunikationssatelliten verwendet. Die Antennen auf dem Boden können fest auf einen bestimmten Punkt ausgerichtet werden, und jeder Satellit deckt stets dasselbe Gebiet der Erde ab. Jedoch fokussieren diese Satelliten ihre Antennen in der Regel auf einzelne Regionen (Ausleuchtungszonen), sodass ein Empfang der Signale gewöhnlich nur in den ausgestrahlten Bereichen möglich ist.
Formeln
Um einen Körper der Masse $ m $ mit der Winkelgeschwindigkeit $ \omega $ auf einer Kreisbahn mit dem Radius $ r $ zu halten, ist eine Zentripetalkraft der Stärke
- $ F_{1}=m\omega ^{2}r $
erforderlich. Auf einer Kreisbahn um einen Planeten ist die Schwerkraft näherungsweise die einzige wirkende Kraft. Im Abstand $ r $ – vom Mittelpunkt des Planeten ausgehend – kann sie mit der Formel
- $ F_{2}={\frac {GMm}{r^{2}}} $
berechnet werden. Dabei bezeichnet $ G $ die Gravitationskonstante und $ M $ die Masse des Planeten.
Da die Schwerkraft also die einzige Kraft ist, die den Körper auf der Kreisbahn hält, muss ihr Wert der Zentripetalkraft entsprechen. Es gilt also:
- $ F_{1}=F_{2} $
Es ergibt sich durch Einsetzen:
- $ m\omega ^{2}r={\frac {GMm}{r^{2}}} $
Auflösen nach $ r $ ergibt:
- $ r={\sqrt[{3}]{G{\frac {M}{\omega ^{2}}}}} $
Die Kreisfrequenz $ \omega $ ergibt sich aus der Umlaufdauer $ t $ als:
- $ \omega ={\frac {2\pi }{t}} $
Einsetzen in die Formel für $ r $ ergibt:
- $ r={\sqrt[{3}]{{\frac {G}{4\pi ^{2}}}Mt^{2}}} $
Diese Formel bestimmt nun den Radius der geostationären Umlaufbahn eines Massenschwerpunktes vom Mittelpunkt des betrachteten Planeten ausgehend.
Um die Entfernung der Bahn von der Oberfläche des Planeten – also beispielsweise die Höhe eines geostationären Satelliten über der Erdoberfläche – zu erhalten, muss dessen Radius vom Ergebnis subtrahiert werden. Somit haben wir:
- $ h={\sqrt[{3}]{{\frac {G}{4\pi ^{2}}}Mt^{2}}}-R_{P} $
wobei $ R_{P} $ den Radius des Planeten bezeichnet.
Wenn der Planet einen Trabanten (z. B. Mond) mit bekannten Bahndaten hat, lässt sich alternativ auch das Dritte Keplersche Gesetz
- $ {\frac {T_{\text{Sat}}^{2}}{T_{\text{Mond}}^{2}}}={\frac {r_{\text{Sat}}^{3}}{r_{\text{Mond}}^{3}}} $
auf Trabant und geostationären Satellit anwenden.
Im Beispiel eines irdischen Satelliten können die Bahndaten des Erdmondes herangezogen werden (Umlaufdauer TMond ≈ 655 h, große Halbachse der Mondumlaufbahn rMond ≈ 384000 km, TSat = 23 h 56 min). Aufgelöst nach dem Bahnradius des geostationären Satelliten, die wegen der Kreisbahn gleich dem Bahnradius ist, ergibt sich damit:
- $ r_{\text{Sat}}={\sqrt[{3}]{\frac {r_{\text{Mond}}^{3}\cdot T_{\text{Sat}}^{2}}{T_{\text{Mond}}^{2}}}}\approx 42000\,\mathrm {km} $
Die Höhe über der Oberfläche des Planeten, hier der Erde, erhält man wieder durch Subtraktion des Planetenradius.
Geschichte
Die Idee eines geostationären Satelliten wurde zuerst von Herman Potočnik in seinem 1928 erschienenen Buch Das Problem der Befahrung des Weltraums – der Raketenmotor veröffentlicht.
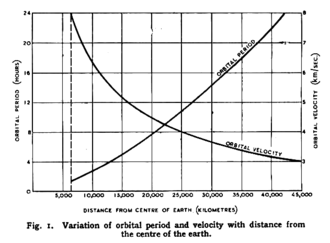
Im Jahre 1945 schlug der Science-Fiction-Autor Arthur C. Clarke vor, Satelliten auf einer geostationären Umlaufbahn zu positionieren. Mit drei Satelliten, jeweils um 120° versetzt, wäre eine weltweite Radiokommunikation möglich. Er nahm an, dass Satelliten dort innerhalb der nächsten 25 Jahre positioniert werden könnten. Mit Syncom 2 im Jahre 1963 in der geosynchronen und Syncom 3 im Jahre 1964 in der geostationären Umlaufbahn wurde seine Idee deutlich zügiger verwirklicht, nach etwa 19 Jahren.
Das Bild rechts zeigt das Diagramm, in dem Clarke seine Überlegungen in der Zeitschrift Wireless World zum ersten Mal der Öffentlichkeit vorstellte.[1]
Siehe auch
Weblinks
- Orbit eines Satelliten im GEO (Memento vom 2. März 2009 im Internet Archive)
- Buchscan: Das Problem der Befahrung des Weltraums. Der Raketen-Motor. von Herman Potočnik alias Hermann Noordung. abgerufen am 21. Januar 2020