Otto-Kreisprozess: Unterschied zwischen den Versionen
79.249.223.167 (Diskussion) |
imported>Tomatenbrille (→Der ideale Otto-Motor: Art des Getriebes sollte hier nicht verschwiegen werden) |
||
| Zeile 6: | Zeile 6: | ||
== Der Vergleichsprozess == | == Der Vergleichsprozess == | ||
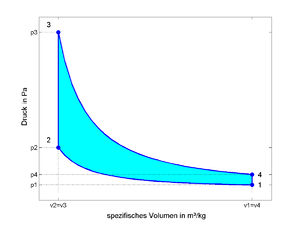
[[Bild:PvDiagramm-Otto.png| | [[Bild:PvDiagramm-Otto.png|mini|300px|p-v-Diagramm des idealen Otto-Prozesses]] | ||
[[Bild:TsDiagramm-Otto.png| | [[Bild:TsDiagramm-Otto.png|mini|300px|T-s-Diagramm des idealen Otto-Prozesses]] | ||
besteht aus vier [[Zustandsänderung]]en eines [[ideales Gas|idealen Gases]] innerhalb eines [[ | besteht aus vier [[Zustandsänderung]]en eines [[ideales Gas|idealen Gases]] innerhalb eines [[Geschlossenes_System_(Thermodynamik)|geschlossenen Systems]]. Er beinhaltet also keine chemische Umsetzung und auch keinen Ladungswechsel. | ||
* 1 - 2 : [[isentrop]]e [[Verdichtungsverhältnis|Kompression]] | * 1 - 2 : [[isentrop]]e [[Verdichtungsverhältnis|Kompression]] | ||
* 2 - 3 : [[Isochore Zustandsänderung|isochore Wärmezufuhr]] (deshalb Gleichraumprozess!) | * 2 - 3 : [[Isochore Zustandsänderung|isochore Wärmezufuhr]] (deshalb Gleichraumprozess!) | ||
| Zeile 20: | Zeile 20: | ||
Zur Veranschaulichung und leichten Berechnung der Zustandsgrößen wird als Arbeitsmedium ein ideales Gas mit temperaturunabhängiger spezifischer Wärmekapazität angenommen. Der thermische [[Wirkungsgrad]] des idealen Otto-Prozesses hängt dann nicht von der zugeführten Wärmemenge ab und lässt sich folgendermaßen bestimmen: | Zur Veranschaulichung und leichten Berechnung der Zustandsgrößen wird als Arbeitsmedium ein ideales Gas mit temperaturunabhängiger spezifischer Wärmekapazität angenommen. Der thermische [[Wirkungsgrad]] des idealen Otto-Prozesses hängt dann nicht von der zugeführten Wärmemenge ab und lässt sich folgendermaßen bestimmen: | ||
::: <math> \eta_{th \, \mathrm {Otto}} = 1 - \frac{1}{\varepsilon^{\ | ::: <math> \eta_{th \, \mathrm {Otto}} = 1 - \frac{1}{\varepsilon^{\kappa-1}} </math> | ||
Je höher das Verdichtungsverhältnis <math>\tfrac{V_1}{V_2}</math> und je höher der [[Isentropenexponent]], desto höher der Wirkungsgrad. | Je höher das Verdichtungsverhältnis <math>\tfrac{V_1}{V_2}</math> und je höher der [[Isentropenexponent]], desto höher der Wirkungsgrad. | ||
| Zeile 27: | Zeile 27: | ||
: <math>\ V_{2} </math> : Kompressionsvolumen | : <math>\ V_{2} </math> : Kompressionsvolumen | ||
: <math> \varepsilon = \frac {V_1}{V_2} </math> : Volumenverhältnis (Verdichtungsverhältnis) | : <math> \varepsilon = \frac {V_1}{V_2} </math> : Volumenverhältnis (Verdichtungsverhältnis) | ||
: <math> \ | : <math> \kappa = \frac{c_p}{c_v} </math> : Isentropenexponent | ||
: <math>\ c_p </math> : [[Spezifische Wärmekapazität]] bei konstantem Druck | : <math>\ c_p </math> : [[Spezifische Wärmekapazität]] bei konstantem Druck | ||
: <math>\ c_v </math> : Spezifische Wärmekapazität bei konstantem Volumen | : <math>\ c_v </math> : Spezifische Wärmekapazität bei konstantem Volumen | ||
Der thermische Wirkungsgrad des Gleichraumprozesses ist bei gleichem Verdichtungsverhältnis höher als der des [[Gleichdruckprozess]]es. | Der thermische Wirkungsgrad des Gleichraumprozesses ist bei gleichem Verdichtungsverhältnis höher als der des [[Gleichdruckprozess]]es. | ||
== Die Gleichungen für die Zustandsänderungen == | == Die Gleichungen für die Zustandsänderungen == | ||
Die spezifische Wärmezufuhr oder Heizenergie <math>q_{zu}</math> bestimmt die Druck- bzw. Temperaturzunahme. Für den Wirkungsgrad spielt sie keine Rolle. | Die spezifische Wärmezufuhr oder Heizenergie <math>q_{zu}</math> bestimmt die Druck- bzw. Temperaturzunahme. Für den Wirkungsgrad spielt sie keine Rolle. | ||
:<math>p_2 = p_1\cdot\varepsilon^\ | :<math>p_2 = p_1\cdot\varepsilon^\kappa</math>; Verdichtungsdruck | ||
:(<math>p_1</math> ist der Anfangsdruck, z. B. 1 bar) | :(<math>p_1</math> ist der Anfangsdruck, z. B. 1 bar) | ||
:<math>T_2 = T_1\cdot\varepsilon^{\ | :<math>T_2 = T_1\cdot\varepsilon^{\kappa-1}</math>; Verdichtungstemperatur | ||
:(<math>T_1</math> ist die Anfangstemperatur vor dem Verdichtungstakt, z. B. 300 K) | :(<math>T_1</math> ist die Anfangstemperatur vor dem Verdichtungstakt, z. B. 300 K) | ||
:<math>T_3 = T_2 + \frac{q_{zu}}{c_v} </math>; Temperatur nach der Wärmezufuhr (Maximale Temperatur) | :<math>T_3 = T_2 + \frac{q_{zu}}{c_v} </math>; Temperatur nach der Wärmezufuhr (Maximale Temperatur) | ||
:(<math>q_{zu}</math> ist die zugeführte spezifische Wärme) | :(<math>q_{zu}</math> ist die zugeführte spezifische Wärme) | ||
:<math> p_3=p_2\cdot \frac{T_3}{T_2}</math>; Druck nach der Wärmezufuhr (Maximaler Druck) | :<math> p_3=p_2\cdot \frac{T_3}{T_2}</math>; Druck nach der Wärmezufuhr (Maximaler Druck) | ||
:<math>p_4 = p_3\cdot\varepsilon^{-\ | :<math>p_4 = p_3\cdot\varepsilon^{-\kappa}</math>; Druck nach der Expansion | ||
== Der ideale Otto-Motor == | == Der ideale Otto-Motor == | ||
[[ | |||
[[File:Ottomotor Vergleichsprozess.svg|rechts|mini|350px|Ottomotor-Vergleichsprozess im p-V-Diagramm, Zusammenhang mit dem stilisierten [[Kurbeltrieb]]]] | |||
Der ideale Motor hat keine [[Dissipation]]sverluste, mechanische Reibungsverluste, Hilfsaggregate, Zylinderkühlung und Dichtigkeitsverluste. Das Arbeitsgas hat über den gesamten Kreisprozess die gleichen Eigenschaften und keine Strömungsverluste. Es gibt keine Durchmischung von Ladungsgemisch mit Abgas. | Der ideale Motor hat keine [[Dissipation]]sverluste, mechanische Reibungsverluste, Hilfsaggregate, Zylinderkühlung und Dichtigkeitsverluste. Das Arbeitsgas hat über den gesamten Kreisprozess die gleichen Eigenschaften und keine Strömungsverluste. Es gibt keine Durchmischung von Ladungsgemisch mit Abgas. | ||
Es gibt Zwei- und Vier-Takt-Motoren. Ein Takt besteht jeweils aus einem Kolbenhub bzw. einer halben Kurbelwellenumdrehung. Beim | Es gibt Zwei- und Vier-Takt-Motoren. Ein Takt besteht jeweils aus einem Kolbenhub bzw. einer halben Kurbelwellenumdrehung. Beim Viertakt-Ottomotor lassen sich die Zustandsänderungen wie folgt den Arbeitstakten zuordnen: | ||
* 1. Takt = Ansaugen: Der Zylinder füllt sich mit [[Frischluft]] 0<math> \rightarrow</math>1. | * 1. Takt = Ansaugen: Der Zylinder füllt sich mit [[Frischluft]] 0<math> \rightarrow</math>1. | ||
* 2. Takt = Verdichten und Wärmezufuhr: [[isentrop]]e Kompression 1<math> \rightarrow</math>2 und [[isochore]] Wärmezufuhr <math>q_{zu}</math> durch Zünden und Verbrennen der Gasladung 2<math> \rightarrow</math>3 im oberen Totpunkt, also bei konstantem Volumen (Gleichraumverbrennung). | * 2. Takt = Verdichten und Wärmezufuhr: [[isentrop]]e Kompression 1<math> \rightarrow</math>2 und [[isochore]] Wärmezufuhr <math>q_{zu}</math> durch Zünden und Verbrennen der Gasladung 2<math> \rightarrow</math>3 im oberen Totpunkt, also bei konstantem Volumen (Gleichraumverbrennung). | ||
| Zeile 58: | Zeile 60: | ||
Gegenüber dem Vergleichsprozess gibt der reale Prozess im Motor zudem eine geringere Arbeit ab, weil: | Gegenüber dem Vergleichsprozess gibt der reale Prozess im Motor zudem eine geringere Arbeit ab, weil: | ||
* das Ansaugen und Ausschieben mit [[Reibung]]sverlusten verbunden ist (linksdrehende Schleife zwischen 0 und 1 im p-V-Diagramm, [[Ladungswechsel]]arbeit) | * das Ansaugen und Ausschieben mit [[Reibung]]sverlusten verbunden ist (linksdrehende Schleife zwischen 0 und 1 im p-V-Diagramm, [[Ladungswechsel]]arbeit) | ||
* die Verbrennung nicht isochor erfolgt, sondern Zeit erfordert, in der sich die Kurbelwelle weiterdreht. Deshalb erfolgt die Zündung vor dem oberen Totpunkt, und die Verbrennung ist erst nach dem o.T. abgeschlossen. Die Spitze im Diagramm bei 3 liegt tiefer und ist abgerundet. | * die Verbrennung nicht isochor erfolgt, sondern Zeit erfordert, in der sich die Kurbelwelle weiterdreht. Deshalb erfolgt die Zündung vor dem oberen Totpunkt, und die Verbrennung ist erst nach dem o. T. abgeschlossen. Die Spitze im Diagramm bei 3 liegt tiefer und ist abgerundet. | ||
* ein Teil der durch die [[chemische Reaktion]] zugeführten Energie (neben unvollständiger Verbrennung und endothermer Bildung von [[Stickoxide|Stickoxid]]) ohne Arbeitsleistung durch Wärmeübergang an die Zylinderwände verloren geht. Der Expansionsverlauf liegt deshalb unterhalb des idealen Verlaufes. | * ein Teil der durch die [[chemische Reaktion]] zugeführten Energie (neben unvollständiger Verbrennung und endothermer Bildung von [[Stickoxide|Stickoxid]]) ohne Arbeitsleistung durch Wärmeübergang an die Zylinderwände verloren geht. Der Expansionsverlauf liegt deshalb unterhalb des idealen Verlaufes. | ||
* das Auslassventil vor dem unteren Totpunkt geöffnet wird. Die Prozessfläche wird im Punkt 4 nach unten abgerundet. | * das Auslassventil vor dem unteren Totpunkt geöffnet wird. Die Prozessfläche wird im Punkt 4 nach unten abgerundet. | ||
| Zeile 74: | Zeile 76: | ||
== Weblinks == | == Weblinks == | ||
*[http://www.unibw.de/lrt10/lehre/thermo/Folien_ThermoI_6_.pdf Thermodynamik Uni München] (PDF; 9,7 MB) | *[https://web.archive.org/web/20120131172352/http://www.unibw.de/lrt10/lehre/thermo/Folien_ThermoI_6_.pdf Thermodynamik Uni München] (PDF; 9,7 MB) | ||
*[http://duepublico.uni-duisburg-essen.de/servlets/DerivateServlet/Derivate-17146/Grundlagen%20der%20Technischen%20Thermodynamik%20mit%20%C3%9Cbungsaufgaben.pdf Uni Duisburg-Essen] (PDF-Datei; 2,50 MB) | *[http://duepublico.uni-duisburg-essen.de/servlets/DerivateServlet/Derivate-17146/Grundlagen%20der%20Technischen%20Thermodynamik%20mit%20%C3%9Cbungsaufgaben.pdf Uni Duisburg-Essen] (PDF-Datei; 2,50 MB) | ||
Aktuelle Version vom 18. Februar 2022, 20:16 Uhr
Der Otto-Kreisprozess (Gleichraumprozess) ist der Vergleichsprozess für den Ottomotor, der nach dem deutschen Erfinder Nicolaus Otto benannten Verbrennungskraftmaschine. Als Thermodynamischer Kreisprozess ist er rechtslaufend, d. h. Wärmeenergie wird in Bewegungsenergie (Arbeit) umgewandelt ($ \rightarrow $ Wärmekraftmaschine).
Die Bezeichnung Gleichraum beruht auf der Annahme, dass die Wärmezufuhr bei gleichbleibendem Volumen (isochor) stattfindet. Dazu im Gegensatz steht der Gleichdruckprozess (auch Diesel-Kreisprozess), bei dem die Wärmezufuhr bei konstantem Druck (isobar) erfolgt. Beide Kreisprozesse eignen sich nicht zur Berechnung der thermodynamischen Verhältnisse in Kolbenmotoren. In der Praxis muss der gemischte Kreisprozess angewandt werden.
Es gab Anfang des 20. Jahrhunderts Gleichraum-Gasturbinen, die den Gleichraumprozess mit zyklischer Verbrennung des Gasgemisches einsetzten. Diese nach seinem Konstrukteur Hans Holzwarth benannten Turbinen brauchten keinen Verdichter. Sie wurden durch die kontinuierlich arbeitenden Gleichdruck-Gasturbinen verdrängt.
Der Vergleichsprozess
besteht aus vier Zustandsänderungen eines idealen Gases innerhalb eines geschlossenen Systems. Er beinhaltet also keine chemische Umsetzung und auch keinen Ladungswechsel.
- 1 - 2 : isentrope Kompression
- 2 - 3 : isochore Wärmezufuhr (deshalb Gleichraumprozess!)
- 3 - 4 : isentrope Expansion
- 4 - 1 : isochore Wärmeabfuhr
Die durch den Linienzug 1-2-3-4 umschlossene Fläche in den Diagrammen entspricht der spezifischen Prozessarbeit $ w $.
Wirkungsgrad
Zur Veranschaulichung und leichten Berechnung der Zustandsgrößen wird als Arbeitsmedium ein ideales Gas mit temperaturunabhängiger spezifischer Wärmekapazität angenommen. Der thermische Wirkungsgrad des idealen Otto-Prozesses hängt dann nicht von der zugeführten Wärmemenge ab und lässt sich folgendermaßen bestimmen:
- $ \eta _{th\,\mathrm {Otto} }=1-{\frac {1}{\varepsilon ^{\kappa -1}}} $
Je höher das Verdichtungsverhältnis $ {\tfrac {V_{1}}{V_{2}}} $ und je höher der Isentropenexponent, desto höher der Wirkungsgrad.
- $ \ V_{1} $ : Anfangsvolumen bzw. Expansionsvolumen
- $ \ V_{2} $ : Kompressionsvolumen
- $ \varepsilon ={\frac {V_{1}}{V_{2}}} $ : Volumenverhältnis (Verdichtungsverhältnis)
- $ \kappa ={\frac {c_{p}}{c_{v}}} $ : Isentropenexponent
- $ \ c_{p} $ : Spezifische Wärmekapazität bei konstantem Druck
- $ \ c_{v} $ : Spezifische Wärmekapazität bei konstantem Volumen
Der thermische Wirkungsgrad des Gleichraumprozesses ist bei gleichem Verdichtungsverhältnis höher als der des Gleichdruckprozesses.
Die Gleichungen für die Zustandsänderungen
Die spezifische Wärmezufuhr oder Heizenergie $ q_{zu} $ bestimmt die Druck- bzw. Temperaturzunahme. Für den Wirkungsgrad spielt sie keine Rolle.
- $ p_{2}=p_{1}\cdot \varepsilon ^{\kappa } $; Verdichtungsdruck
- ($ p_{1} $ ist der Anfangsdruck, z. B. 1 bar)
- $ T_{2}=T_{1}\cdot \varepsilon ^{\kappa -1} $; Verdichtungstemperatur
- ($ T_{1} $ ist die Anfangstemperatur vor dem Verdichtungstakt, z. B. 300 K)
- $ T_{3}=T_{2}+{\frac {q_{zu}}{c_{v}}} $; Temperatur nach der Wärmezufuhr (Maximale Temperatur)
- ($ q_{zu} $ ist die zugeführte spezifische Wärme)
- $ p_{3}=p_{2}\cdot {\frac {T_{3}}{T_{2}}} $; Druck nach der Wärmezufuhr (Maximaler Druck)
- $ p_{4}=p_{3}\cdot \varepsilon ^{-\kappa } $; Druck nach der Expansion
Der ideale Otto-Motor
Der ideale Motor hat keine Dissipationsverluste, mechanische Reibungsverluste, Hilfsaggregate, Zylinderkühlung und Dichtigkeitsverluste. Das Arbeitsgas hat über den gesamten Kreisprozess die gleichen Eigenschaften und keine Strömungsverluste. Es gibt keine Durchmischung von Ladungsgemisch mit Abgas.
Es gibt Zwei- und Vier-Takt-Motoren. Ein Takt besteht jeweils aus einem Kolbenhub bzw. einer halben Kurbelwellenumdrehung. Beim Viertakt-Ottomotor lassen sich die Zustandsänderungen wie folgt den Arbeitstakten zuordnen:
- 1. Takt = Ansaugen: Der Zylinder füllt sich mit Frischluft 0$ \rightarrow $1.
- 2. Takt = Verdichten und Wärmezufuhr: isentrope Kompression 1$ \rightarrow $2 und isochore Wärmezufuhr $ q_{zu} $ durch Zünden und Verbrennen der Gasladung 2$ \rightarrow $3 im oberen Totpunkt, also bei konstantem Volumen (Gleichraumverbrennung).
- 3. Takt = Arbeitstakt: Isentrope Expansion 3$ \rightarrow $4.
- 4. Takt = Ausblastakt (Wärmeabfuhr): Durch das Öffnen des Auslassventils expandieren die Abgase im unteren Totpunkt ohne weitere Arbeitsleistung nach außen 4$ \rightarrow $1, und der Rest wird durch den Kolbenhub 1$ \rightarrow $0 nach außen geschoben. Dabei wird die im Abgas enthaltene Wärme $ q_{ab} $ an die Umgebung abgegeben. Der ideale Prozess berücksichtigt nicht, dass die Restmenge im Kompressionsraum nicht den Umgebungszustand erreicht.
Der reale Otto-Motor
Beim realen Ottomotor begrenzt die Klopffestigkeit des Gasgemisches den Verdichtungsdruck. Die Zustandsänderungen des Gleichraumprozesses entsprechen nicht dem realen Motor, da für die Verbrennung Zeit erforderlich ist (s. u.). Mit einem entsprechend angepassten Seiliger-Kreisprozess erhält man eine wesentlich bessere Annäherung. Das Luft-Gasgemisch beim Verdichten und die Brenngase beim Expandieren haben unterschiedliche Stoffeigenschaften und sind stark temperaturabhängig (kleinerer Isentropenexponent und größere Wärmekapazität bei hohen Temperaturen). Abgase (verbrannte Luft, hauptsächlich Stickstoff, Wasserdampf und Kohlenstoffdioxid) haben andere thermodynamische Eigenschaften als Luft-Gasgemische oder Frischluft. Deshalb ist auch der Seiligerprozess für realitätsnahe Berechnungen zu ungenau. Gegenüber dem Vergleichsprozess gibt der reale Prozess im Motor zudem eine geringere Arbeit ab, weil:
- das Ansaugen und Ausschieben mit Reibungsverlusten verbunden ist (linksdrehende Schleife zwischen 0 und 1 im p-V-Diagramm, Ladungswechselarbeit)
- die Verbrennung nicht isochor erfolgt, sondern Zeit erfordert, in der sich die Kurbelwelle weiterdreht. Deshalb erfolgt die Zündung vor dem oberen Totpunkt, und die Verbrennung ist erst nach dem o. T. abgeschlossen. Die Spitze im Diagramm bei 3 liegt tiefer und ist abgerundet.
- ein Teil der durch die chemische Reaktion zugeführten Energie (neben unvollständiger Verbrennung und endothermer Bildung von Stickoxid) ohne Arbeitsleistung durch Wärmeübergang an die Zylinderwände verloren geht. Der Expansionsverlauf liegt deshalb unterhalb des idealen Verlaufes.
- das Auslassventil vor dem unteren Totpunkt geöffnet wird. Die Prozessfläche wird im Punkt 4 nach unten abgerundet.
Das Verhältnis von im Motor freigesetzter zu theoretischer Arbeit des Prozesses wird als Gütegrad bezeichnet. Reale Motoren haben zusätzlich eine mechanische Verlustleistung aus Reibung und der erforderlichen Leistung für Neben- und Hilfsantriebe (Ventile, Pumpen für Öl und Kühlwasser, Ventilator), die ca. 10 % der Nennleistung betragen kann und den Wirkungsgrad weiter vermindern.
Literatur
Siehe auch
- Gleichdruckprozess bzw. Diesel-Prozess
- Seiliger-Prozess (gemischter Vergleichsprozess beim Kolbenmotor)
- Carnot-Prozess (theoretisch maximaler thermodynamischer Wirkungsgrad)
- Joule-Prozess (Gleichdruckprozess bei der Turbine)
Weblinks
- Thermodynamik Uni München (PDF; 9,7 MB)
- Uni Duisburg-Essen (PDF-Datei; 2,50 MB)
fr:Cycle de Beau de Rochas#Étude thermodynamique