Tunnelionisation: Unterschied zwischen den Versionen
- Wikipedia:Vorlagenfehler/Vorlage:Literatur/Interner Fehler
- Atomphysik
imported>KLBot2 K (Bot: 2 Interwiki-Link(s) nach Wikidata (d:Q285050) migriert) |
imported>Aka K (Tippfehler entfernt, Leerzeichen in Überschrift, deutsch, Kleinkram) |
||
| Zeile 1: | Zeile 1: | ||
'''Tunnelionisation''' ist ein Vorgang, bei dem Elektronen durch die [[Potentialbarriere]] aus einem Atom oder Molekül entweichen. In einem starken elektrischen Feld wird die Potentialbarriere eines Atoms oder Moleküls drastisch verzerrt. Dadurch verringert sich die | '''Tunnelionisation''' ist ein Vorgang, bei dem Elektronen durch die [[Potentialbarriere]] aus einem Atom oder Molekül entweichen. In einem starken elektrischen Feld wird die Potentialbarriere eines Atoms oder Moleküls drastisch verzerrt. Dadurch verringert sich die Breite der Barriere, die Elektronen überwinden müssen, so dass sie leichter aus dem Atom oder Molekül entweichen können (siehe [[Tunneleffekt]]). Die Tunnelionisation ist ein [[Quanteneffekt]]: nach den klassischen Gesetzen kann ein Teilchen auch die verformte Coulomb-Barriere nicht überwinden, da es dazu zu wenig Energie hat. | ||
== DC Tunnelionisation == | |||
Die Tunnelionisation aus dem Grundzustand eines [[Wasserstoffatom]]s in einem elektrostatischen (DC) Feld wurde zuerst von [[Cornelius Lanczos]] untersucht<ref>{{Literatur |Sammelwerk=Zeitschrift für Physik |Datum=1931-03 |Band=68 |Nummer=3–4 |Seiten=204-232 |Titel=Zur Intensitätsschwächung der Spektrallinien in hohen elektrischen Feldern |Autor= [[Cornelius Lanczos]] |DOI=10.1007/BF01390967 |Sprache=de |Online=https://link.springer.com/content/pdf/10.1007%2FBF01390967.pdf}}</ref>. | |||
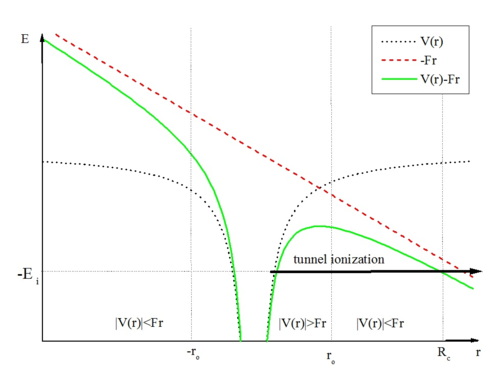
[[Datei:Tunnel ionization 3.png|right|mini|400px|Potential eines Atoms in einem externen konstanten elektrischen Feld. Für kleine Abstände vom Atomkern <math>r \ll r_0</math>, kann das Potential des externen Feldes vernachlässigt werden, während für größere Abstände <math>r \gg r_0</math>, das Coulombpotential gegenüber dem externen Potential vernachlässigbar ist. Das Elektron verlässt die Barriere bei <math>r=R_c</math>; <math>E_i</math> ist das Ionisationspotential des Atoms.]] | |||
Landau-Lifschitz skizzieren eine vereinfachte Ableitung<ref>{{Literatur |Autor=[[Lew Dawidowitsch Landau|L. D. Landau]] und [[Jewgeni Michailowitsch Lifschitz|E. M. Lifschitz]] |Titel=Quantenmechanik |Verlag=Akademie Verlag |Ort=Berlin |Jahr=1985 |Auflage=7. |Seiten=283ff}}</ref> für ein Teilchen der Masse <math>m</math> und Ladung <math>e</math>, die die richtige exponentielle Abhängigkeit der Ionisationrsate vom angewandten äußeren Feld liefert. Wenn <math>E \ll E_a </math> ist, ist die Ionisationsrate gegeben durch: | |||
:<math> w = 4 \omega_a \frac{E_a}{\left|E\right|} \exp\left[ -\frac{2}{3}\frac{E_a}{\left|E\right|} \right]</math> | |||
Die Parameter <math>E_a, \omega_a</math> sind in [[Internationales Einheitensystem|SI-Einheiten]] gegeben durch: | |||
:<math>E_a = \frac{m^2 e^5}{(4\pi \varepsilon_0)^3 \hbar^4} </math>, | |||
:<math>\omega_a = \frac{m e^4}{(4\pi \varepsilon_0)^2 \hbar^3}</math>, | |||
wobei <math>\hbar</math> das [[Plancksches Wirkungsquantum|reduzierte Plancksche Wirkungsquantum]] und <math>\varepsilon_0</math> die [[Elektrische Feldkonstante|Permittivität des Vakuums]] sind. Die Ionisationsrate ist der Gesamt[[wahrscheinlichkeitsstrom]] durch den äußeren klassischen Umkehrpunkt. Dieses Ergebnis kann mithilfe der [[WKB-Näherung]] abgeleitet werden. | |||
== AC Tunnelionisation == | |||
Die Ionisationsrate eines Wasserstoffatom in einem elektrischen Wechselfeld, wie es zum Beispiel durch einen [[Laser]] erzeugt wird, lässt sich in einem geeigneten Grenzfall als eine DC Ionisationsrate berechnen (wobei die Feldstärke über eine Periode der Oszillation des elektrischen Feldes gemittelt wird).<ref>{{Literatur |Sammelwerk=JETP |Band=20 |Nummer=5 |Seiten=1307 |Datum=1965-05 |Kommentar=Russisches Original: ZhETF, Bd. 47, Nr. 5, S. 1945 |Titel=Ionization in the Field of a Strong Electromagnetic Wave | |||
|Autor=L. V. Keldysh |Sprache=en |DOI= |Online=http://www.jetp.ac.ru/cgi-bin/dn/e_020_05_1307.pdf |Zugriff=2018-01-18 |Format=pdf}}</ref> | |||
In einem periodischen Wechselfeld kehrt sich die Feldrichtung in jeder Halbperiode um. Elektronen, die vom Atom oder Molekül wegbeschleunigt wurden, werden daher eine Halbperiode später wieder zu ihm hin beschleunigt. Bei diesem Vorgang [[Rekombination (Physik)|rekombinieren]] einige Elektronen mit dem Atom bzw. Molekül. Da sie viel kinetische Energie mitbringen, wird überschüssige Energie als energiereiches Licht freigesetzt. Man kann so auf effiziente Weise [[Ultraviolettstrahlung]] oder [[Röntgenstrahlung]] erzeugen. Wenn keine Rekombination erfolgt, kann es zu weiterer Ionisation der Atome oder Moleküle durch Kollision mit den energiereichen Elektronen kommen, wodurch Ionen höherer [[Wertigkeit (Chemie)]] entstehen. | |||
== Weblinks == | |||
* {{Literatur |Online=http://www.wissenschaft.de/home/-/journal_content/56/12054/1625620 |Sammelwerk=Bild der Wissenschaft |Titel=Zeitlos im Quantentunnel |Autor=Axel Tillemans |Datum=2010-05-18 |Zugriff=2018-01-18}} | |||
* {{Internetquelle |url=http://www.pro-physik.de/details/news/2050623/Der_Ionisation_von_Helium_in_Zeitlupe_zugeschaut.html |titel=Der Ionisation von Helium in Zeitlupe zugeschaut |datum=2012-05-15 |autor=TU Wien/OD |werk=prophysik.de |zugriff=2018-01-19}} | |||
== Literatur == | |||
* {{Literatur |Sammelwerk=Zeitschrift für Physik |Datum=1931-03 |Band=68 |Nummer=3–4 |Seiten=204-232 |Titel=Zur Intensitätsschwächung der Spektrallinien in hohen elektrischen Feldern |Autor= [[Cornelius Lanczos]] |DOI=10.1007/BF01390967 |Sprache=de |Online=https://link.springer.com/content/pdf/10.1007%2FBF01390967.pdf}} | |||
* {{Literatur |Titel=Tunnel and multiphoton ionization of atoms and ions in a strong laser field (Keldysh theory) |Autor=Vladimir S Popov |DOI=10.1070/PU2004v047n09ABEH001812 | |||
|Datum=2004 |Sammelwerk=Phys.-Usp. |Band=47 |Seiten=855}} | |||
* {{Literatur |Titel=Strong-Field Induced Atomic Excitation and Kinematics |Autor=U. Eichmann |Sammelwerk=Ultrafast Dynamics Driven by Intense Light Pulses. From Atoms to Solids, from Lasers to Intense X-rays |Hrsg= Markus Kitzler und Stefanie Gräfe |ISBN=978-3-319-20172-6 |DOI=10.1007/978-3-319-20173-3 |Online=http://www.springer.com/cda/content/document/cda_downloaddocument/9783319201726-c1.pdf?SGWID=0-0-45-1519230-p177416205 |Zugriff=2018-01-18 |Sprache=en |Format=pdf |Datum=2016}} | |||
* {{Literatur |Titel=Tunnelionisation in starken Laserfeldern |Autor=Ümit Aydin |Sammelwerk=Diplomarbeit in Physik (Fakultät für Mathematik, Informatik und Naturwissenschaften, RWTH Aachen) |Datum=2002-09 |Online=http://llp.ilt.fhg.de/skripten/diplom_aydin.pdf |Zugriff=2018-01-18}} | |||
== Einzelnachweise == | |||
<references /> | |||
[[Kategorie:Atomphysik]] | [[Kategorie:Atomphysik]] | ||
Aktuelle Version vom 2. Juli 2020, 14:20 Uhr
Tunnelionisation ist ein Vorgang, bei dem Elektronen durch die Potentialbarriere aus einem Atom oder Molekül entweichen. In einem starken elektrischen Feld wird die Potentialbarriere eines Atoms oder Moleküls drastisch verzerrt. Dadurch verringert sich die Breite der Barriere, die Elektronen überwinden müssen, so dass sie leichter aus dem Atom oder Molekül entweichen können (siehe Tunneleffekt). Die Tunnelionisation ist ein Quanteneffekt: nach den klassischen Gesetzen kann ein Teilchen auch die verformte Coulomb-Barriere nicht überwinden, da es dazu zu wenig Energie hat.
DC Tunnelionisation
Die Tunnelionisation aus dem Grundzustand eines Wasserstoffatoms in einem elektrostatischen (DC) Feld wurde zuerst von Cornelius Lanczos untersucht[1].
Landau-Lifschitz skizzieren eine vereinfachte Ableitung[2] für ein Teilchen der Masse $ m $ und Ladung $ e $, die die richtige exponentielle Abhängigkeit der Ionisationrsate vom angewandten äußeren Feld liefert. Wenn $ E\ll E_{a} $ ist, ist die Ionisationsrate gegeben durch:
- $ w=4\omega _{a}{\frac {E_{a}}{\left|E\right|}}\exp \left[-{\frac {2}{3}}{\frac {E_{a}}{\left|E\right|}}\right] $
Die Parameter $ E_{a},\omega _{a} $ sind in SI-Einheiten gegeben durch:
- $ E_{a}={\frac {m^{2}e^{5}}{(4\pi \varepsilon _{0})^{3}\hbar ^{4}}} $,
- $ \omega _{a}={\frac {me^{4}}{(4\pi \varepsilon _{0})^{2}\hbar ^{3}}} $,
wobei $ \hbar $ das reduzierte Plancksche Wirkungsquantum und $ \varepsilon _{0} $ die Permittivität des Vakuums sind. Die Ionisationsrate ist der Gesamtwahrscheinlichkeitsstrom durch den äußeren klassischen Umkehrpunkt. Dieses Ergebnis kann mithilfe der WKB-Näherung abgeleitet werden.
AC Tunnelionisation
Die Ionisationsrate eines Wasserstoffatom in einem elektrischen Wechselfeld, wie es zum Beispiel durch einen Laser erzeugt wird, lässt sich in einem geeigneten Grenzfall als eine DC Ionisationsrate berechnen (wobei die Feldstärke über eine Periode der Oszillation des elektrischen Feldes gemittelt wird).[3]
In einem periodischen Wechselfeld kehrt sich die Feldrichtung in jeder Halbperiode um. Elektronen, die vom Atom oder Molekül wegbeschleunigt wurden, werden daher eine Halbperiode später wieder zu ihm hin beschleunigt. Bei diesem Vorgang rekombinieren einige Elektronen mit dem Atom bzw. Molekül. Da sie viel kinetische Energie mitbringen, wird überschüssige Energie als energiereiches Licht freigesetzt. Man kann so auf effiziente Weise Ultraviolettstrahlung oder Röntgenstrahlung erzeugen. Wenn keine Rekombination erfolgt, kann es zu weiterer Ionisation der Atome oder Moleküle durch Kollision mit den energiereichen Elektronen kommen, wodurch Ionen höherer Wertigkeit (Chemie) entstehen.
Weblinks
- Axel Tillemans: Zeitlos im Quantentunnel. In: Bild der Wissenschaft. 18. Mai 2010 (wissenschaft.de [abgerufen am 18. Januar 2018]).
- TU Wien/OD: Der Ionisation von Helium in Zeitlupe zugeschaut. In: prophysik.de. 15. Mai 2012, abgerufen am 19. Januar 2018.
Literatur
- Vladimir S Popov: Tunnel and multiphoton ionization of atoms and ions in a strong laser field (Keldysh theory). In: Phys.-Usp. Band 47, 2004, S. 855, doi:10.1070/PU2004v047n09ABEH001812.
- Ümit Aydin: Tunnelionisation in starken Laserfeldern. In: Diplomarbeit in Physik (Fakultät für Mathematik, Informatik und Naturwissenschaften, RWTH Aachen). September 2002 (fhg.de [PDF; abgerufen am 18. Januar 2018]).
Einzelnachweise
- ↑
- ↑ L. D. Landau und E. M. Lifschitz: Quantenmechanik. 7. Auflage. Akademie Verlag, Berlin 1985, S. 283 ff.
- ↑