Sachs-Wolfe-Effekt
Der Sachs-Wolfe-Effekt (nach Rainer K. Sachs und Arthur M. Wolfe, die ihn 1967 entdeckten) erklärt Fluktuationen der Rotverschiebung der Photonen der kosmischen Hintergrundstrahlung. Er ist neben der Silk-Dämpfung und akustischen Schwingungen des Plasmas im frühen Universum einer von drei Effekten, mit denen es in der Astrophysik möglich ist, Zustände im frühen Universum zu berechnen.
Er ermöglicht es, aus den Fluktuationen der Rotverschiebung der kosmischen Hintergrundstrahlung abzulesen, wie die Materiestruktur im Weltall zur Zeit der Rekombination, etwa 400.000 Jahre nach dem Urknall, gewesen sein muss. Insbesondere lässt sich damit der Krümmungsparameter k der Raumzeit feststellen.
Sachs-Wolfe-Gleichung
Die Sachs-Wolfe-Gleichung zur Bestimmung der Fluktuationen der Temperatur $ T $ der kosmischen Hintergrundstrahlung lautet:
- $ \Theta (\eta _{0},{\vec {x}}_{0},-{\hat {n}})=\Theta _{0}(\eta _{0},{\vec {x}}_{0})+{\frac {\delta T}{\bar {T}}}(\eta _{0},{\vec {x}}_{0},-{\hat {n}}) $
Dabei bezeichnet
- $ \eta $ die konforme Zeit
- $ {\vec {x}} $ den Ortsvektor
- $ {\hat {n}} $ den Richtungseinheitsvektor
- $ \Theta _{0} $ den richtungsunabhängigen Monopol der kosmischen Hintergrundstrahlung, der der isotropen Durchschnittstemperatur entspricht.
Exakte Gleichung
Die Sachs-Wolfe-Gleichung ergibt sich aus der linearisierten Boltzmann-Gleichung für kleine Störungen zu:
- $ \Theta (\eta _{0},-{\hat {n}})=\int _{\eta _{*}}^{\eta _{0}}\left(g(\eta )(\Theta _{0}+\psi +{\hat {n}}\cdot {\vec {\nabla }}v_{b})+e^{-\tau }(\phi '+\psi ')\right)\mathrm {d} \eta -\psi (\eta _{0},{\vec {x}}_{0}) $
Dabei bezeichnet:
- $ g(\eta ) $ die visibility function; die Wahrscheinlichkeit, dass ein Photon der kosmischen Hintergrundstrahlung, das heute beobachtet wird, zu einer bestimmten Zeit $ \eta $ zuletzt gestreut wurde,
- $ \tau $ die optische Dicke,
- $ \psi ,\phi $ Störungen der FLRW-Metrik in der zeitartigen/raumartigen Komponente; im Newtonschen Grenzfall kann $ \psi $ als Störung des Gravitationspotentials verstanden werden,
- $ {\vec {\nabla }}v_{b} $ die Geschwindigkeit der baryonischen Materie und
- eine gestrichene Größe' die partielle Ableitung nach der konformen Zeit: $ '=\partial /\partial \eta $
Genäherte Gleichung
Nimmt man an, dass keine Reionisierung stattgefunden hat, so kann die visibility function angenähert werden durch eine Delta-Distribution zum Zeitpunkt $ \eta _{\text{dec}} $ der Entkopplung der Photonen (decoupling):
- $ g(\eta )=g(\eta -\eta _{\text{dec}}) $
Dies führt direkt dazu, dass das Exponential der optischen Tiefe als Heaviside-Funktion $ \Theta $ geschrieben werden kann:
- $ e^{-\tau }=\Theta (\eta -\eta _{\text{dec}}) $
Dadurch wird die approximierte Sachs-Wolfe-Gleichung zu
- $ \Theta (\eta _{0},{\vec {x}}_{0},-{\hat {n}})=(\Theta _{0}+\psi +{\hat {n}}\cdot {\vec {\nabla }}v_{b}){\big |}_{\eta _{\text{dec}},{\vec {x}}_{\text{lss}}}+\int _{\eta _{\text{dec}}}^{\eta _{0}}(\phi '+\psi ')\mathrm {d} \eta -\psi (\eta _{0},{\vec {x}}_{0}) $
Erläuterung
Nicht-integrierter Sachs-Wolfe-Effekt
Der nicht-integrierte Sachs-Wolfe-Effekt rührt daher, dass zum Zeitpunkt der Entkopplung der Photonen von der Materie im Universum an einigen Stellen Gebiete existierten, deren Gravitationspotential vom isotropen Hintergrund abwich. Aufgrund dieser Potentialunterschiede erfahren die Photonen, die von einem Gebiet mit höherem/niedrigeren Gravitationspotential stammen, eine relative gravitative Rot-/Blauverschiebung. Diesem Effekt wird in der Gleichung durch die Differenz $ \psi (\eta _{\text{dec}},{\vec {x}}_{\text{lss}})-\psi (\eta _{0},{\vec {x}}_{0}) $ entsprochen.
Der nicht-integrierte Sachs-Wolfe-Effekt ist der bedeutendste Term in der Sachs-Wolfe-Gleichung.
Integrierter Sachs-Wolfe-Effekt
Während der Propagation der Photonen durch das Universum treffen sie weiter auf die Anisotropien der baryonischen Materie. Im Fall eines statischen Universums würden die Photonen aufgrund der Energieerhaltung beim Verlassen einer Anisotropie dieselbe Energie wieder aufnehmen, die sie beim Eintritt in die Anisotropie abgegeben haben. Da sich das Universum in der Zeit jedoch ausgedehnt hat, flacht das Gravitationspotential ab, während das Photon die Anisotropie passiert. Dies ist der integrierte Sachs-Wolfe-Effekt, dargestellt durch den Term
- $ \int _{\eta _{\text{dec}}}^{\eta _{0}}(\phi '+\psi ')\mathrm {d} \eta $.
Im Lauf der Entwicklung des Universums entstehen durch Strukturbildung weitere Anisotropien; diese sind jedoch vernachlässigbar.
Andere Komponenten der Sachs-Wolfe-Gleichung
Die anderen beiden Terme der Sachs-Wolfe-Gleichung lassen sich ohne kosmologische Effekte oder die Allgemeine Relativitätstheorie klassisch erklären:
- $ \Theta (\eta _{\text{dec}}) $ bezeichnet die intrinsischen Temperaturfluktuationen der Photonen zum Zeitpunkt der Entkopplung.
- $ {\hat {n}}\cdot {\vec {\nabla }}v_{b} $ ist der klassische Doppler-Effekt aus der Relativbewegung des Baryonen-Photonen-Fluids zum Beobachter.
Messungen
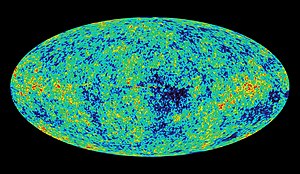
Mit WMAP ist es im Jahre 2001 gelungen, durch den Sachs-Wolfe-Effekt starke Hinweise auf die Existenz der hypothetischen dunklen Energie zu erhalten. Diese in ihrer Natur noch unbekannte Energie ist verantwortlich für die Expansion des Universums und würde etwa 70 % seiner Energie ausmachen.
Der Krümmungsparameter k der Raumzeit ergab sich aus den Messungen zu k = 0, was bedeutet, dass das Universum eine flache Mannigfaltigkeit darstellt. Da eine perfekte Messung jedoch unmöglich ist, kann das Universum sehr schwach gekrümmt sein und dies im Bereich des Messfehlers liegen.
Im Mai 2009 wurde das ESA-Teleskop Planck gestartet, das eine zehn Mal genauere Auflösung der Hintergrundstrahlung lieferte und bessere Untersuchungen ermöglichte.
Literatur
- R. K. Sachs, A. M. Wolfe: Perturbations of a Cosmological Model and Angular Variations of the Microwave Background. In: The Astrophysical Journal. Band 147, 1967, ISSN 0004-637X, S. 73, doi:10.1086/148982.
Videos
- Was ist der Sachs-Wolfe-Effekt? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 23. Nov. 2005.