Hydrostatik

Die Hydrostatik ist die Lehre von unbewegten, strömungsfreien Flüssigkeiten. Sie ist ein Teilgebiet der Fluidstatik.

Hydrostatischer Druck

Der Druck in einer idealen Flüssigkeit an einem Punkt ist in alle Richtungen gleich. Wirkt nur die Schwerkraft, so entspricht der Schweredruck (auch hydrostatischer Druck) der Summe aus dem (Atmosphären-)Druck an der Oberfläche und dem sich durch das Gewicht der Flüssigkeitssäule über dem betrachteten Punkt ergebenden Druck. Der Schweredruck ist nur von der Tiefe, nicht jedoch von der Gefäßform abhängig. Dies wird als hydrostatisches Paradoxon bezeichnet.

Hydrostatische Grundgleichung

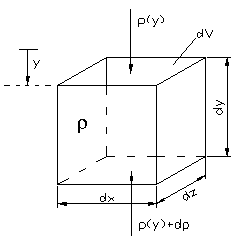
Zur Herleitung der hydrostatischen Grundgleichung macht man folgende Betrachtung: Im Erdschwerefeld mit der Fallbeschleunigung $ g $ wirkt auf das druckbelastete quaderförmige Volumenelement $ dV=dx\cdot dy\cdot dz $ der Dichte $ \rho $, von oben der Druck $ p(y) $. Von unten (aus pos. in die neg. y-Richtung) wirkt ein Gegendruck $ p(y)+dp $.

Zwischen Ober- und Unterseite des Volumenelementes gibt es also einen Druckzuwachs $ dp $, den es zu bestimmen gilt. Hierzu wird das Kräftegleichgewicht in y-Richtung $ \sum F_{y}=0 $ aufgestellt:

$ \sum F_{y}=p(y)\cdot (dx\cdot dz)+\rho \cdot (dx\cdot dy\cdot dz)\cdot g-(p(y)+dp)\cdot (dx\cdot dz)=0 $

dieser Ausdruck lässt sich kürzen zu

$ \rho \cdot dy\cdot g-dp=0 $

Umgeschrieben ergibt sich die als "hydrostatische Grundgleichung" bekannte Form:

$ {\frac {dp}{dy}}=\rho \cdot g $

Der Vollständigkeit halber sei erwähnt, dass sich dieser Zusammenhang auch als Sonderfall der Navier-Stokes-Gleichungen aus der Fluidmechanik ergibt. Diese werden mithilfe des Impulssatzes für ein Fluidelement hergeleitet.

Aus der hydrostatischen Grundgleichung ergibt sich unter Annahme der Inkompressibilität von Flüssigkeiten ($ \rho ={\rm {const.}} $) für den von y abhängigen Druck p(y):

$ \int _{p(0)}^{p(h)}dp=\int _{0}^{h}(\rho g)dy $

$ \Rightarrow p(h)=\rho \cdot g\cdot h+p(0) $

mit

$ \rho $: Dichte der Flüssigkeit

$ g $: Schwerebeschleunigung

$ h $: Ausdehnung der Flüssigkeitssäule in $ y $-Richtung

$ p(y=0) $: Druck an der Oberfläche der Flüssigkeitssäule

Bezieht man die Kompressibilität des Fluids in die Berechnung des Drucks mit ein, ergibt sich mit der Kompressibilität $ \kappa =-{\frac {dV}{V\cdot dp}}=0{,}5{\frac {1}{\rm {GPa}}} $ das folgende Diagramm:

In 12.000 m Tiefe ergäbe sich hiermit, ausgehend von einer Dichte von 1000 kg/m³ in 0 m Tiefe, eine Abweichung des berechneten realen Drucks vom idealen von ca. 3,5 %. Hierbei bleiben jedoch weiterhin Temperatureffekte ebenso wie andere Einflüsse unberücksichtigt.

Unter Ansatz eines entsprechenden Ausdrucks für $ \rho $ lässt sich in ähnlicher Weise die barometrische Höhenformel aus der hydrostatischen Grundgleichung entwickeln.

Statischer Auftrieb

Wird ein Körper in eine Flüssigkeit gebracht, so ist der Druck an der Unterseite höher als an der Oberseite. Die resultierende Kraft weist nach oben und heißt Auftrieb. Die Auftriebskraft entspricht der Gewichtskraft der verdrängten Flüssigkeit (Archimedisches Prinzip). Ist die durchschnittliche Dichte eines Körpers kleiner als die der Flüssigkeit, so überwiegt die Auftriebskraft gegenüber der Gewichtskraft. Wirken dann nicht noch andere Kräfte auf ihn ein, steigt der Körper nach oben und schwimmt. Ist seine Dichte hingegen größer als die Flüssigkeit, sinkt der Körper nach unten, bei gleicher Dichte schwebt er.

Hydraulik

Hydraulische Systeme nutzen die Unabhängigkeit des Druckes von der Gefäßform aus. Wird beispielsweise Wasser durch ein Rohr mit relativ kleinem Querschnitt A₁ in ein Gefäß mit großen Querschnitt A₂ gedrückt, so ist der Druck p im Rohr gleich dem Druck im Gefäß. Die aufzuwendende Kraft im Rohr ist F₁=p·A₁. Die Kraft im Gefäß wirkt aber auf die gesamte Querschnittsfläche. Sie ist F₂=p·A₂ und damit um ein Vielfaches größer. Das hydraulische System wirkt hier als Kraftverstärker. Anwendung findet dieses Prinzip z. B. in der hydraulischen Presse.

Literatur

• Dionysius Lardner:Handbuch der Hydrostatik und Pneumatik. Druck und Verlag von Gottfried Basse, Quedlinburg und Leipzig 1836.
• Abel Bürja:Grundlehren der Hydrostatik. Bei Lagarde und Friedrich, Berlin 1790.
• Bruno Eck:Technische Strömungslehre. Springer Verlag Berlin Heidelberg GmbH, Berlin Heidelberg 1949.

Weblinks

• 

  Wikibooks: Formelsammlung Hydrostatik – Lern- und Lehrmaterialien
• Vorlesungsskript Hydrostatik (abgerufen am 4. Januar 2015)
• Hydrostatik (abgerufen am 4. Januar 2015)
• Fluidmechanik (abgerufen am 4. Januar 2015)