Bedeckungsveränderlicher Stern
- Wikipedia:Vorlagenfehler/Vorlage:Cite journal/Parameter language fehlt
- Sternklasse der Veränderlichen Sterne
- Sternklasse der Doppelsterne
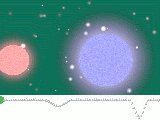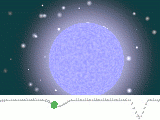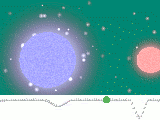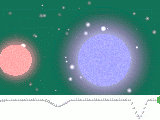
Ein bedeckungsveränderlicher Stern oder fotometrischer Doppelstern ist ein Doppelsternsystem, dessen Bahn so im Raum liegt, dass sich die beiden Sterne von der Erde aus gesehen periodisch verdecken.
Der Prototyp dieser Doppelsterne ist Algol (β Persei) im Sternbild Perseus, den die Araber im Mittelalter Teufelsstern nannten. Seine Veränderlichkeit wurde bereits in der Antike bemerkt und seine genaue Periodizität 1783/84 von John Goodricke in den Philosophical Transactions veröffentlicht.[1] Algols Helligkeit sinkt alle 2,87 Tage auf ein Drittel ab und zeigt in der halben Periode ein kleines Nebenminimum.
Analyse der Lichtkurve
Aus der Lichtkurve, der Änderung der Helligkeit des nicht aufgelösten Doppelsternsystems während eines Umlaufs um den gemeinsamen Schwerpunkt, können die folgenden Parameter abgeleitet werden:
- Die Umlaufzeit
- Die Dauer des Haupt- und des Nebenminimums
- Die eventuelle Dauer des Stillstands im Minimum im Fall einer totalen Bedeckung
- Die Amplituden der Minima
- Der Helligkeitsverlauf im Abfall und Anstieg der Minima
Aus diesen Daten kann auf die Flächenhelligkeiten der Sterne, die relativen Radien, die Bahnneigung, die Randverdunkelung, die Gravitationsverdunkelung, die Abweichung von der Kugelform durch Zentrifugalkräfte und der relative Abstand geschlossen werden. Wird die Beobachtung in einem fotometrischen System in mehreren Wellenlängen durchgeführt, kann auch auf die Oberflächentemperatur der Sterne geschlossen werden. Da Sterne nur einen begrenzten Bereich von Zustandsgrößen annehmen können, ist damit eine Bestimmung der absoluten Parameter wie Leuchtkraft und von geometrischen Parametern, z.B. Sternradien, möglich.
Wird der Verlauf der Radialgeschwindigkeit mittels des Dopplereffekts bestimmt, können auch die Massen der Sterne sowie die Bahnexzentrizität berechnet werden. Da nur bei bedeckungsveränderlichen Sternen die Bahnneigung eines optisch nicht in seine Komponenten auflösbaren Doppelsternsystems bestimmt werden kann, sind sie die wichtigste Quelle zur Bestimmung von Sternmassen.[2]
Klassifizierung
Es gibt zwei Hauptklassifizierungen für Bedeckungsveränderliche anhand der Lichtkurve und den geometrischen Verhältnissen:[3]
Lichtkurve
- Algolsterne zeigen eine annähernd konstante Helligkeit zwischen den Minima
- Bei Beta-Lyrae-Sternen ist der Lichtwechsel kontinuierlich veränderlich mit abgerundeten Maxima, aber unterschiedlich tiefen Minima. Die Umlaufdauer liegt zwischen einem und bis zu 20 Tagen.
- Die W-Ursae-Maioris-Sterne ähneln den Beta-Lyrae-Sternen ohne Stillstände, wobei die Minima annähernd gleich tief sind. Die Umlaufdauer ist kürzer als ein Tag.
Geometrische Verhältnisse
- Getrennte Systeme, die zwischen den Komponenten keinen Materieaustausch zeigen.
- Halbgetrennte Systeme, bei denen einen Komponente die maximale Ausdehnung im Doppelsternsystem eingenommen hat. Bei jeder weiteren Expansion dieser Komponente würde Materie zum Begleiter fließen.
- Bei Kontaktsystemen hat jede Komponente die maximale Ausdehnung angenommen und es besteht ein beständiger Materieaustausch zwischen den beiden Sternen.
Sonderformen
Neben Sternen können auch nichtleuchtende Begleiter eine Bedeckung verursachen. Dazu gehören Exoplaneten, Braune Zwerge und Staubscheiben wie im Fall Epsilon Aurigae. Weil diese Objekte nicht selbst leuchten, wird nur ein Rückgang der Helligkeit bei einem Bedeckungsveränderlichen pro Umlauf beobachtet. Planeten und braune Zwerge haben einen wesentlich kleineren Durchmesser als Sterne und deshalb ist die Helligkeitsänderung im Minimum gering. Die notwendige Messgenauigkeit lässt sich außerhalb der Erdatmosphäre mit wesentlich geringerem Instrumentenaufwand erreichen, speziell bei der gleichzeitigen und lange andauernden Überwachung einer großen Anzahl von Sternen zur Suche nach solchen Minima. So sind zum Beispiel die primären Ziele der Satellitenmissionen Kepler und COROT die Suche nach Exoplaneten mittels der Transitmethode.[4]
Daneben gibt es auch Dreifach-Bedeckungssysteme wie KOI-126. Hier umläuft in einer exzentrischen Bahn ein Stern ein enges Doppelsternsystem, wobei beide Sterne des engen Systems von dem ausgedehnten Begleiter bedeckt werden können. Die Lichtkurve erscheint unregelmäßig veränderlich aufgrund der Überlagerung der Minima.[5]
Nutzen für die Astrophysik

Der astrophysikalische Nutzen dieser Sternenklasse besteht in der Möglichkeit durch Messung der Lichtkurve auf die Bahndaten und physikalischen Zustandsgrößen der Sterne in dem Doppelsternsystem schließen zu können. So ist es mit Hilfe der neuen Generation von Großteleskopen möglich, bedeckungsveränderliche Sterne innerhalb der lokalen Gruppe zu finden und zu untersuchen. Durch die Ableitung der Leuchtkraft aus der Lichtkurve konnten die Entfernungen zu den Magellanschen Wolken, dem Andromedanebel, dem Dreiecksnebel und einigen Zwerggalaxien der lokalen Gruppe mit einer Genauigkeit von bis zu 6 % bestimmt werden.[6]
Bedeckungsveränderliche erlauben weiterhin die räumliche Auflösung von Strukturen auf oder nahe den Sternen des Doppelsternsystems. Dazu gehören:
- Die einander zugewandten Hemisphären der Sterne sind heller durch den Reflexionseffekt bei engen Doppelsternsystemen
- Sternflecken ähnlich den Sonnenflecken
- Fackeln ähnlich den Sonnenfackeln
- Materieströme zwischen den Sternen
- Ringe und Akkretionsscheiben um den Masseempfänger
- Heiße Flecken an der Sternoberfläche, wo Materieströme aufprallen und ihre Bewegungsenergie freisetzen
- Bei den Zeta-Aurigae- und VV-Cephei-Systemen wird ein Hauptreihenstern als Lichtquelle zur Durchleuchtung und Analyse der ausgedehnten Atmosphäre eines Roten Riesen genutzt.
Die Beobachtung einer Apsidendrehung der Bahn eines Bedeckungsveränderlichen ist relativ einfach, da in diesem Fall sich die Position des Haupt- und des Nebenminima relativ zueinander verändern. Da die Apsidendrehung auch abhängig von dem Aufbau der Sterne in dem Doppelsternsystem ist können Bedeckungsveränderliche auch zur Verifizierung von Modellen der inneren Struktur von Sternen genutzt werden.[7] Allerdings müssen dafür die Rotationsparameter und die Ausrichtung der Achsen bekannt sein wie im Falle DI Herculis.[8] Die Apsidendrehung kann auch zur Falsifikation von alternativen Gravitationstheorien genutzt werden. Mit diesen Hypothesen können die beobachteten Abweichungen der Rotationskurven von Galaxien, die dynamische Stabilität von Galaxienhaufen und die Gravitationslinsen durch Galaxien oder Cluster ebenso gut erklärt werden wie durch die Annahme von dunkler Materie. Die beobachteten Apsidendrehungen bei bedeckungsveränderlichen Sternen mit einer großen Bahnexzentrizität sollten in einigen Jahren von denen nach der Relativitätstheorie berechneten Werten abweichen und eine Unterscheidung ermöglichen.[9]
Da mit dem Abstand auch die Wahrscheinlichkeit einer gegenseitigen Bedeckung der Sterne abnimmt haben die meisten Bedeckungsveränderlichen kurze Perioden und daher eine kleine Bahnhalbachse im Verhältnis zu den Sternradien. Dadurch kann die Entwicklung der Sterne in Doppelsternsystemen von der von Einzelsternen abweichen aufgrund von Masseaustausch zwischen den Komponenten, beschleunigter Rotation und magnetischer Aktivität.
Periodenänderungen
Änderungen in dem Gesamtdrehimpuls des Doppelsternsystems oder in der Verteilung des Drehimpuls sollten zu einer Verschiebung des Zeitpunkts minimaler Helligkeit führen. Da sich die Änderung mit jedem Umlauf kumuliert sind kleinste Abweichungen messbar und Beobachtungen zeigen, dass die Umlaufzeiten vieler bedeckungsveränderlicher Sterne nicht konstant sind.[10][11] Dabei sind folgende Phänomene bekannt, die eine Periodenänderung auslösen oder vortäuschen können:
- Apsidendrehung
- Beim Lichtlaufzeiteffekt umkreist ein dritter Körper das Doppelsternsystem und verschiebt damit den Schwerpunkt, um den sich die beiden Sterne des Bedeckungsveränderlichen bewegen. Aufgrund der Endlichkeit der Lichtgeschwindigkeit verschiebt dies den Zeitpunkt minimaler Helligkeit.
- Massenaustausch zwischen den Komponenten
- Massenverlust aus dem Doppelsternsystem z. B. durch Sternwinde
- Abstrahlung von Gravitationswellen
- Der magnetische Drehimpulsverlust entsteht, wenn ein Stern ionisiertes Gas entlang der Magnetfeldlinien des Sterns verliert. Das Gas ist in den Magnetfeldlinien eingefroren bis zu dem Radius, bei dem das Magnetfeld mit Lichtgeschwindigkeit rotiert. Die Folge ist eine Abnahme der Rotationsgeschwindigkeit des Sterns und damit ein Verlust von Drehimpuls im Doppelsternsystem.
- Beim Applegate-Mechanismus wird Drehimpuls im Laufe eines magnetischen Zyklus umverteilt zwischen der inneren und äußeren Konvektionszone eines Sterns. Dies führt zu einer Änderung der Rotationsabplattung und damit indirekt auch der Umlaufdauer, die dabei sowohl zunehmen und als auch abnehmen kann. Nach Beobachtungen treten zyklische Periodenzu- und -abnahmen fast ausschließlich nur bei bedeckungsveränderlichen Sternen auf, bei denen wenigstens eine Komponente magnetische Aktivität zeigt.[12]
- Eine asymmetrische Helligkeitsverteilung auf der zu bedeckenden Hemisphäre durch Sternflecken
- Durch Gezeitenkräfte ausgelöste Pulsationen, die häufig in Resonanz mit der Umlaufdauer des Doppelsterns sind.
Die meisten beobachteten Periodenänderungen bei bedeckungsveränderlichen Sternen werden dem Massenaustausch zwischen den Komponenten der Doppelsternsysteme zugeschrieben. Allerdings ist die Ursache vieler zyklischer Periodenänderungen nicht bekannt.
Änderung der Lichtkurve
Läuft ein dritter Stern um das gemeinsame Massenzentrum und liegt seine Umlaufbahn dabei nicht in der Ebene des Bedeckungsveränderlichen so führt dies zu einer Präzession der Bahn des engen Doppelsternsystems. In der Folge verändert sich die Inklination der Bahn und damit auch die Tiefe der Minima. Insgesamt ist nur eine geringe Zahl an Dreifachsystemen bekannt mit einer veränderlichen Tiefe der Minima aufgrund des gravitativen Einflusses eines dritten Körpers. Zu diesen Sternen gehören Algol und HS Hydrae.[13]
Daneben kann auch die Normalhelligkeit schwanken aufgrund von Änderungen an der Oberfläche von einer oder beiden Komponenten des Bedeckungsveränderlichen. Zu den bekanntesten Beispielen gehören die RS-Canum-Venaticorum-Sterne. Auf der Oberfläche eines späten Riesen bilden sich Sternflecken mit einem Radius bis zu 20° und einer Temperatur, die circa 1500 K unterhalb der ungestörten Sternoberfläche liegt. Dies führt zu Einsenkungen in den Lichtkurven, die im Laufe von Monaten bis Jahren durch die Lichtkurve wandern. Bei Bedeckungsveränderlichen ist aufgrund der gebundenen Rotation die Rotationsperiode identisch mit der Bahnumlaufdauer. Das langsame Wandern der Sternflecken über die Oberfläche ist daher die Folge einer differentiellen Rotation in den späten Riesen.[14] Auch bedeckungsveränderliche BY-Draconis-Sterne zeigen eine vergleichbare Modulation der Lichtkurve. Bei dieser Sternklasse handelt es sich um späte Zwerge mit Sternflecken auf ihren Oberflächen.[15]
Wenn ein Planet seinem Zentralstern zu nahe kommt, heizt er sich so weit auf, dass Teile seiner Oberfläche verdampfen und die Materie das Gravitationsfeld des Super Mercury verlassen können. Wenn die Bahn des Planeten von der Erde aus gesehen vor dem Stern vorbeiführt, kann es zu einer veränderlichen Tiefe und Dauer des Bedeckungsminima kommen. Dabei ist die Umlaufdauer konstant wie im Fall von KIC 12557548, wo die Tiefe der Minima zwischen 0,2 % und 1,2 % schwankt. Die verdampfte Materie kondensiert in einer Entfernung vom Stern wieder zu Staub und absorbiert das Sternlicht sehr effektiv. Die Bedeckungslichtkurve ist asymmetrisch und wie bei allen Planetentransits fehlt das sekundäre Minimum.[16]
Weblinks
- Sternwarte Hagen – interaktives Java-Applet zur Veranschaulichung der Geometrie und der resultierenden Lichtkurven (nebst theoretischer Behandlung).
Quellen
- ↑ z.B. Zdenek Kopal: Dynamics of Close Binary Systems. 1978 (1914), S. 3 unten; The Philosophical Transactions of the Royal Society of London, from Their Commencement in 1665 to the Year 1800. veröffentlicht 1809, S. 456ff
- ↑ W. Strohmeier: Veränderliche Sterne. Treugesell-Verlag, Düsseldorf 1974.
- ↑ John R. Percy: Understanding Variable Stars. Cambridge University Press, Cambridge 2007, ISBN 978-0-521-23253-1.
- ↑ Alfred Weigert, Heinrich Johannes Wendker, Lutz Wisotzki: Astronomie und Astrophysik. Ein Grundkurs.
- ↑ Joshua A. Carter u. a.: KOI-126: A Triply-Eclipsing Hierarchical Triple with Two Low-Mass Stars. In: Astrophysics. Solar and Stellar Astrophysics. 2011, arxiv:1102.0562v1.
- ↑ Alceste Z. Bonanos: Eclipsing Binaries: Tools for Calibrating the Extragalactic Distance Scale. In: Binary Stars as Critical Tools and Tests in Contemporary Astrophysics, International Astronomical Union. Symposium no. 240, held 22–25 August, 2006 in Prague, Czech Republic, S240, #008. 2006, arxiv:astro-ph/0610923.
- ↑ P. Zasche: On the apsidal-motion of thirteen eclipsing binaries. In: Astrophysics. Solar and Stellar Astrophysics. 2012, arxiv:1204.5578v1.
- ↑ S. Albrecht, S. Reffert, I. Snellen: Misaligned spin and orbital axes cause the anomalous precession of DI Herculis. In: Nature. Band 461, 2009, S. 373–376, doi:10.1038/nature08408.
- ↑ M. De Laurentis, R. De Rosa, F. Garufi, L. Milano: Testing gravitational theories using Eccentric Eclipsing Detached Binaries. In: Astrophysics. Solar and Stellar Astrophysics. 2012, arxiv:1207.5410v1.
- ↑ Cuno Hoffmeister, G. Richter, W. Wenzel: Veränderliche Sterne. J. A. Barth Verlag, Leipzig 1990, ISBN 3-335-00224-5.
- ↑ D. R. Gies, S. J. Williams, R. A. Matson, Z. Guo, S. M. Thomas: A Search for Hierarchical Triples using Kepler Eclipse Timing. In: Astrophysics. Solar and Stellar Astrophysics. 2012, arxiv:1204.0030v1.
- ↑ Jetsu, L., Porceddu, S., Lyytinen, J., Kajatkari, P., Lehtinen, J., Markkanen, T, Toivari-Viitala, J.: Did the Ancient Egyptians Record the Period of the Eclipsing Binary Algol – The Raging One? In: The Astrophysical Journal. 773. Jahrgang, Nr. 1, 2013, S. A1 (14pp), doi:10.1088/0004-637X/773/1/1, bibcode:2013ApJ...773....1J.
- ↑ P. Zasche and A. Paschke: HS Hydrae about to turn off its eclipses. In: Astronomy & Astrophysics. Band 542, 2012, S. L23, doi:10.1051/0004-6361/201219392.
- ↑ Arnold, C. N., Montle, R. E., Stuhlinger, T. W., & Hall, D. S.: UBV photometry and light curve solution of the eclipsing RS CVn binary SS Cam. In: Acta Astronomica. Band 29, 1979, S. 243–258.
- ↑ J. MacDonald and D. J. Mullan: Precision modeling of M dwarf stars: the magnetic components of CM Draconis. In: Astrophysics. Solar and Stellar Astrophysics. 2011, arxiv:1106.1452v1.
- ↑ M. Brogi, C. U. Keller, M. de Juan Ovelar, M. A. Kenworthy, R. J. de Kok, M. Min, I. A. G. Snellen: Evidence for the disintegration of KIC 12557548 b. In: Astrophysics. Solar and Stellar Astrophysics. 2012, arxiv:1208.2988.