Elektrische Kapazität
- Seiten mit Skriptfehlern
- Wikipedia:Vorlagenfehler/Vorlage:Cite journal/Parameter language fehlt
- Elektrische Größe
- Elektrostatik
- Physikalische Größenart
| Physikalische Größe | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Elektrische Kapazität | |||||||||||||||
| Formelzeichen | $ C $ | |||||||||||||||
| ||||||||||||||||
Die elektrische Kapazität (Formelzeichen $ C $, von lateinisch capacitas ‚Fassungsvermögen‘; Adjektiv kapazitiv) ist eine physikalische Größe aus dem Bereich der Elektrostatik, Elektronik und Elektrotechnik.
Die elektrische Kapazität zwischen zwei voneinander isolierten elektrisch leitenden Körpern ist gleich dem Verhältnis der Ladungsmenge $ Q $, die auf diesen Leitern gespeichert ist ($ +Q $ auf dem einen und $ -Q $ auf dem anderen), und der zwischen ihnen herrschenden elektrischen Spannung $ U $:
- $ C={\frac {Q}{U}} $
Sie wird dabei festgelegt durch die Dielektrizitätskonstante des isolierenden Mediums sowie die Geometrie der Körper, dazu zählt auch der Abstand. Dadurch stehen (sofern die Kapazität konstant ist) $ Q $ und $ U $ zueinander in einer proportionalen Beziehung.
Bei Akkumulatoren sowie Batterien benutzt man den Begriff „Kapazität“ für die maximale Ladungsmenge $ Q $, welche in ihnen gespeichert werden kann. Sie wird in Amperestunden (Ah) angegeben. Diese Kapazität der elektrischen Ladung hat jedoch weder etwas mit der hier dargestellten elektrischen Kapazität (Farad) noch mit der Leistungskapazität (Watt) zu tun.
Kapazität eines Kondensators
Eine technische Anwendung findet die Kapazität in Form von elektrischen Kondensatoren, welche durch die Angabe einer bestimmten Kapazität charakterisiert werden. Der Begriff „Kapazität“ wird umgangssprachlich auch synonym für das elektrische Bauelement Kondensator selbst (englisch capacitor) verwendet.
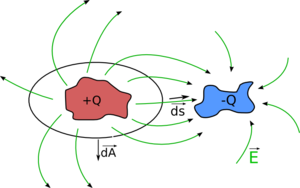
Ein Kondensator ist eine Leiteranordnung mit zwei Elektroden zur getrennten Speicherung von elektrischer Ladung $ +Q $ und $ -Q $. In physikalischer Sicht rührt der elektrische Fluss $ \Psi $ von den getrennten elektrischen Ladungen $ +Q $ und $ -Q $ her, die von der externen Spannungsquelle mit der Spannung $ U $ auf die Elektroden transportiert werden, womit sich:
- $ Q=C\cdot U $
ergibt. Formal erfolgt dieser Zusammenhang über das Gaußsche Gesetz. Die elektrische Kapazität eines Kondensators kann dann als das Verhältnis der Ladungsmenge $ Q $ zur angelegten Spannung $ U $ ausgedrückt werden:
- $ C={\frac {Q}{U}} $.
Dabei ist $ C $ üblicherweise eine konstante Kenngröße, die sich wie folgt ergibt.
Ein Körper, auf den eine positive elektrische Ladung gegeben wird, hat dadurch ein elektrisches Feld, das der Bewegung einer weiteren positiven elektrischen Ladung auf den Körper entgegenwirkt. Befindet sich nun aber ein Körper in der Nähe, der negativ geladen ist, so wird das abstoßende elektrische Feld des positiven Körpers geschwächt (die auf den Körper zu bewegende positive Ladung spürt auch die Kraft der anziehenden negativen Ladung). Damit wird weniger Spannung benötigt um die weitere positive Ladung auf den bereits positiv geladenen Körper zu bewegen, als ohne den zweiten, negativ geladenen Körper. Der erste Körper hat also eine höhere Kapazität. Das Gleiche gilt natürlich auch für den zweiten Körper. Die Abschwächung des elektrischen Feldes durch den einen geladenen Körper auf den anderen geladenen Körper wird beeinflusst durch deren Geometrie und die Permittivität des isolierenden Mediums zwischen den beiden Körpern.
In einer vereinfachten Analogie entspricht die Kapazität dem Volumen eines Druckluftbehälters mit konstanter Temperatur. Der Luftdruck ist dabei analog zur Spannung $ U $ und die Luftmenge analog zur Ladungsmenge $ Q $. Daher ist die Ladungsmenge im Kondensator proportional zur Spannung.
Diese Gesetzmäßigkeit gilt auch für die sogenannte Pseudokapazität, einer innerhalb enger Grenzen spannungsabhängigen elektrochemischen bzw. faradayschen Speicherung elektrischer Energie, die mit in einer Redoxreaktion und mit einem Ladungsaustausch an Elektroden von Superkondensatoren verbunden ist, wobei allerdings im Gegensatz zu Akkumulatoren an den Elektroden keine chemische Stoffänderung eintritt.
Unter anderem die Physikalisch-Technische Bundesanstalt (PTB) befasst sich mit Kapazitätsnormalen.
Einheit
Die elektrische Kapazität wird in der abgeleiteten SI-Einheit Farad gemessen. Ein Farad (1 F) ist diejenige Kapazität, die beim Anlegen einer Spannung von 1 Volt eine Ladungsmenge von 1 Coulomb (1 C = 1 As) speichert:
- $ [C]={\frac {[Q]}{[U]}}={\frac {1\,\mathrm {C} }{1\,\mathrm {V} }}={\frac {1\,\mathrm {As} }{1\,\mathrm {V} }}=1\,\mathrm {F} $
Ein Kondensator der Kapazität 1 Farad lädt sich bei einem konstanten Ladestrom von 1 Ampere in 1 Sekunde auf die Spannung 1 Volt auf. Die SI-Einheit Farad, genannt zu Ehren des englischen Physikers und Chemikers Michael Faraday, hat sich heutzutage international überall durchgesetzt.
Veraltete Einheit
Bis Mitte des 20. Jahrhunderts wurde die Kapazität von Kondensatoren häufig mit der Kapazitätseinheit cm beschriftet. Diese Angabe in Zentimetern rührt daher, dass die Kapazität im heute praktisch kaum noch gebrauchten Gaußschen Einheitensystem in der Längendimension ausgedrückt wird. So weist eine Metallkugel mit 5 cm Radius gegenüber einer sich im Unendlichen befindlichen Gegenelektrode eine Kapazität von 5 cm auf.
Die nebenstehende Abbildung zeigt einen Papierkondensator der Marke SATOR der ehemaligen Firma Kremenezky, Mayer & Co aus dem Jahr 1950 mit einer Kapazität von 5000 cm. Das entspricht der Kapazität einer Metallkugel von 5000 cm Radius. Dargestellt im heute üblichen SI-Einheitensystem sind das ca. 5,6 nF.
Eine Kapazität von 1 cm im Gaußschen Einheitensystem entspricht ca. 1,1 pF im SI-Einheitensystem, der Umrechnungsfaktor ist 4πε0. Diese Umrechnung kommt durch die Definition der Feldkonstante im Gaußschen Einheitensystem zustande:
- $ \varepsilon _{0}:={\frac {1}{4\pi }} $ im Gaußschen Einheitssystem (nicht im Internationalen Einheitensystem (SI))
Kapazität bestimmter Leiteranordnungen
Für die Kapazität einer Reihe von einfachen Leiteranordnungen gibt es analytische Lösungen oder konvergente Reihenentwicklungen. Die folgende Tabelle zeigt einige Beispiele:
| Bezeichnung | Kapazität | Schematische Darstellung |
|---|---|---|
| Plattenkondensator | $ C=\varepsilon \cdot {\frac {A}{d}} $ | |
| Plattenkondensator unterschiedlich große Platten[1] |
$ C={\frac {2\varepsilon }{d}}\cdot {\frac {A_{1}A_{2}}{A_{1}+A_{2}}} $ | |
| Koaxialkabel oder Zylinderkondensator |
$ C=2\pi \varepsilon \,{\frac {l}{\ln \!\left({\frac {R_{2}}{R_{1}}}\right)}} $ | |
| Kugelkondensator | $ C={\frac {4\pi \varepsilon }{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}}} $ | |
| Kugel, Gegenelektrode mit $ R_{2} $ gegen unendlich |
$ C=4\pi \varepsilon \cdot R_{1} $ | |
| Parallele Zylinder (Lecher-Leitung) |
$ C={\frac {\pi \varepsilon l}{\operatorname {arcosh} \left({\frac {d}{2R}}\right)}} $ | |
| Ein Leiter parallel über ebener Fläche. |
$ C={\frac {2\pi \varepsilon l}{\operatorname {arcosh} \left({\frac {d}{R}}\right)}} $ | $ d>R $ |
| Zwei Kugeln mit identischem Radius $ a $[2][3] |
$ C=2\pi \varepsilon a\sum _{n=1}^{\infty }{\frac {\sinh \left(\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}{\sinh \left(n\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}} $ $ =2\pi \varepsilon a\left\{1+{\frac {1}{2D}}+{\frac {1}{4D^{2}}}+{\frac {1}{8D^{3}}}+{\frac {1}{8D^{4}}}+{\frac {3}{32D^{5}}}+{\mathcal {O}}\left({\frac {1}{D^{6}}}\right)\right\} $ $ =2\pi \varepsilon a\left\{\ln 2+\gamma -{\frac {1}{2}}\ln \left(2D-2\right)+{\mathcal {O}}\left(2D-2\right)\right\} $ |
$ d $: Abstand der Kugeln, $ d>2a $ |
| Kreisscheibe[4] gegen unendlich |
$ C=8\varepsilon a $ | $ a $: Radius |
| Gerades Drahtstück (langer Zylinder)[5][6][7] gegen unendlich |
$ C={\frac {2\pi \varepsilon l}{\Lambda }}\left\{1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left[1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right]+{\mathcal {O}}\left({\frac {1}{\Lambda ^{3}}}\right)\right\} $ | $ l $: Länge $ a $: Drahtradius $ \Lambda $: $ \ln(l/a) $ |
Hierin bezeichnet ggf. A die Fläche der Elektroden, d deren Abstand, l deren Länge, $ R_{1} $ sowie $ R_{2} $ deren Radien und $ \varepsilon $ die Permittivität (dielektrische Leitfähigkeit) des Dielektrikums. Es gilt $ \varepsilon =\varepsilon _{0}\varepsilon _{\mathrm {r} } $, wobei $ \varepsilon _{0} $ für die elektrische Feldkonstante und $ \varepsilon _{\mathrm {r} } $ für die relative Permittivität steht. In der schematischen Darstellung sind die Leiter hellgrau bzw. dunkelgrau und das Dielektrikum blau gefärbt.
Berechnungen zur Kapazität
Folgende allgemeine Gleichungen für die Bestimmung der Kapazität gelten für die jeweils zeitabhängigen Größen Strom $ i(t) $, Spannung $ u(t) $ und Ladung $ q(t) $ an einer konstanten elektrischen Kapazität $ C $:
- $ i(t)={\frac {\mathrm {d} q(t)}{\mathrm {d} t}}=C\cdot {\frac {\mathrm {d} u(t)}{\mathrm {d} t}} $
- $ u(t)={\frac {1}{C}}\cdot \int i(t)\,\mathrm {d} t $
Ein Ausdruck für die Kapazität einer beliebigen Elektrodenanordnung oder Ladungsverteilung lässt sich mittels des Gaußschen Satzes herleiten:
- $ C={\frac {Q}{U}}={\frac {\oint _{A}{\vec {D}}\cdot \mathrm {d} {\vec {A}}}{\int _{s}{\vec {E}}\cdot \mathrm {d} {\vec {s}}}} $
Dabei beträgt die dielektrische Verschiebung $ {\vec {D}}=\varepsilon _{0}\cdot \varepsilon _{\mathrm {r} }\cdot {\vec {E}} $, also:
- $ C=\varepsilon _{0}\cdot \varepsilon _{\mathrm {r} }\cdot {\frac {\oint _{A}{\vec {E}}\cdot \mathrm {d} {\vec {A}}}{\int _{s}{\vec {E}}\cdot \mathrm {d} {\vec {s}}}} $
Für ein Vakuum vereinfacht sich diese Gleichung wegen $ \varepsilon _{r}=1 $ zu:
- $ C=\varepsilon _{0}\cdot {\frac {\oint _{A}{\vec {E}}\cdot \mathrm {d} {\vec {A}}}{\int _{s}{\vec {E}}\cdot \mathrm {d} {\vec {s}}}} $
Eine Berechnung der Kapazität erfordert die Kenntnis des elektrischen Feldes. Hierfür ist die Laplace-Gleichung $ \nabla ^{2}\varphi =0 $ mit einem konstanten Potential $ \varphi $ auf den Leiteroberflächen zu lösen. In komplizierteren Fällen existiert keine geschlossene Form der Lösung.
Messen der Kapazität
Das Messen der Kapazität dient nicht nur der Kontrolle der Kapazität eines Kondensators (Bauteil), sondern wird beispielsweise in kapazitiven Abstandssensor zur Abstandsbestimmung herangezogen. Auch weitere Sensoren (Druck, Feuchte, Gase) beruhen oft auf einer Kapazitätsmessung.
Entsprechend den oben genannten Zusammenhängen kann die Kapazität folgendermaßen bestimmt werden:
- Laden mit konstantem Strom und Beobachten der Spannungsanstiegsgeschwindigkeit
- Messen der Resonanzfrequenz eines mit der Kapazität gebildeten LC-Schwingkreises
- Anlegen einer Wechselspannung und Messen des Stromverlaufes
Insbesondere das letztgenannte Verfahren wird in Kapazitätsmessgeräten angewendet, wobei nicht nur die Größe des Stromes, sondern auch seine Phasenlage zur Spannung erfasst wird. Auf diese Weise kann auch die Impedanz und der Verlustwinkel bzw. der Gütefaktor des Kondensators bestimmt werden.
Literatur
- Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretische Elektrotechnik. 18. Auflage. Springer, 2008, ISBN 978-3-540-78589-7.
Einzelnachweise und Anmerkungen
- ↑ capacitance of a parallel plate capacitor with different areas. 2017, abgerufen am 21. September 2021 (Lua-Fehler in Modul:Multilingual, Zeile 149: attempt to index field 'data' (a nil value)).
- ↑ J. C. Maxwell: A Treatise on Electricity and Magnetism. Dover, 1873, ISBN 0-486-60637-6, S. 266 ff.
- ↑ A. D. Rawlins: Note on the Capacitance of Two Closely Separated Spheres. In: IMA Journal of Applied Mathematics. 34. Jahrgang, Nr. 1, 1985, S. 119–120, doi:10.1093/imamat/34.1.119.
- ↑ J. D. Jackson: Classical Electrodynamics. Wiley, 1975, S. 128, problem 3.3.
- ↑ J. C. Maxwell: On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness. In: Proc. London Math. Soc. IX. Jahrgang, 1878, S. 94–101, doi:10.1112/plms/s1-9.1.94.
- ↑ L. A. Vainshtein: Static boundary problems for a hollow cylinder of finite length. III Approximate formulas. In: Zh. Tekh. Fiz. 32. Jahrgang, 1962, S. 1165–1173.
- ↑ J. D. Jackson: Charge density on thin straight wire, revisited. In: Am. J. Phys. 68. Jahrgang, Nr. 9, 2000, S. 789–799, doi:10.1119/1.1302908, bibcode:2000AmJPh..68..789J.