Bremsstrahlung: Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Elektrodynamik
- Strahlung
imported>Ra-raisch K (Link korrigiert) |
imported>Wiesebohm (Die letzte Textänderung von 109.90.24.18 wurde verworfen und die Version 200306948 von Blaues-Monsterle wiederhergestellt.) |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:Bremsstrahlung.svg| | [[Datei:Bremsstrahlung.svg|mini|Erzeugung von Röntgenbremsstrahlung durch Abbremsung eines schnellen Elektrons im Coulombfeld eines [[Atomkern]]s (schematische Darstellung)]] | ||
'''Bremsstrahlung''' ist die [[elektromagnetische Welle|elektromagnetische Strahlung]], die | '''Bremsstrahlung''' ist die [[elektromagnetische Welle|elektromagnetische Strahlung]], die durch die [[Beschleunigung]] eines [[Elektrische Ladung|elektrisch geladenen]] Teilchens, z. B. eines [[Elektron]]s, entsteht. Entgegen der Namensgebung tritt diese Strahlung nicht nur dann auf, wenn sich der Betrag der Geschwindigkeit verringert, sondern auch, wenn er sich vergrößert oder die Geschwindigkeit nur ihre Richtung verändert. Von Bremsstrahlung im engeren Sinne spricht man, wenn Teilchen in [[Materie]] gebremst werden. | ||
Vom Standpunkt der [[Quantenelektrodynamik]] aus lässt sich die Erzeugung von Bremsstrahlung erklären, dass jede Wechselwirkung von geladenen Teilchen mit der Emission oder Absorption von [[Photon]]en, den Quanten der elektromagnetischen Strahlung, verbunden ist. | |||
== Auftreten bzw. Anwendung == | == Auftreten bzw. Anwendung == | ||
| Zeile 9: | Zeile 9: | ||
Der Effekt der Bremsstrahlung wird in [[Röntgenröhre]]n zur Erzeugung von [[Röntgenstrahlung]] verwendet. Dabei schießt man Elektronen mit einer [[kinetische Energie|kinetischen Energie]] ab 30 k[[Elektronenvolt|eV]] auf eine Metallplatte, die häufig aus [[Wolfram]] besteht. Ein kleiner Teil der beim Abbremsen frei werdenden Energie wird in Röntgenstrahlung mit einem kontinuierlichen [[Spektrum (Physik)|Spektrum]] (einem '''Röntgenkontinuum''') umgewandelt. | Der Effekt der Bremsstrahlung wird in [[Röntgenröhre]]n zur Erzeugung von [[Röntgenstrahlung]] verwendet. Dabei schießt man Elektronen mit einer [[kinetische Energie|kinetischen Energie]] ab 30 k[[Elektronenvolt|eV]] auf eine Metallplatte, die häufig aus [[Wolfram]] besteht. Ein kleiner Teil der beim Abbremsen frei werdenden Energie wird in Röntgenstrahlung mit einem kontinuierlichen [[Spektrum (Physik)|Spektrum]] (einem '''Röntgenkontinuum''') umgewandelt. | ||
Bremsstrahlung kann außerdem die Entwicklung und [[Morphologie]] [[Elektrische Entladung|elektrischer Entladungen]] beeinflussen<ref>Köhn, C., Chanrion, O., Neubert, T. The influence of bremsstrahlung on electric discharge streamers in N<sub>2</sub>, O<sub>2</sub> gas mixtures Plasma Sources Sci. Technol. (2017), vol. 26, 015006 | Bremsstrahlung kann außerdem die Entwicklung und [[Morphologie]] [[Elektrische Entladung|elektrischer Entladungen]] beeinflussen<ref>Köhn, C., Chanrion, O., Neubert, T. The influence of bremsstrahlung on electric discharge streamers in N<sub>2</sub>, O<sub>2</sub> gas mixtures Plasma Sources Sci. Technol. (2017), vol. 26, 015006. {{DOI|10.1088/0963-0252/26/1/015006}}.</ref> sowie hochenergetische [[Terrestrischer Gammablitz|terrestrische Gammablitze]] und [[Positron]]en erzeugen.<ref>Köhn, C., Ebert, U. Calculation of beams of positrons, neutrons, and protons associated with terrestrial gamma ray flashes Journal Geophys. Res. (2015), vol. 120, pp. 1620–1635. {{DOI|10.1002/2014JD022229}}.</ref> | ||
associated with terrestrial gamma ray flashes Journal Geophys. Res. (2015), vol. 120, pp. | |||
== Physik der Bremsstrahlung == | |||
Das elektromagnetische Feld bewegter Ladungen wird durch die [[Liénard-Wiechert-Potential]]e beschrieben. Danach sind das elektrische Feld <math>\vec E</math> und das magnetische Feld <math>\vec B</math> durch | |||
:<math>\begin{align} | |||
\vec E(\vec x,t) &= \frac{q}{4\pi \varepsilon_0} \left[\frac{\vec n - \vec \beta}{\gamma^2(1-\vec \beta \cdot \vec n)^3 R^2}\right]_\text{ret} + \frac{q}{4\pi \varepsilon_0 c} \left[\frac{\vec n \times [(\vec n -\vec \beta)\times \dot \vec \beta]}{(1- \vec \beta \cdot \vec n)^3 R}\right]_\text{ret} \\ | |||
\vec B(\vec x,t) &= \frac 1c \left[\vec n \times \vec E\right]_\text{ret} | |||
\end{align} | |||
</math> | |||
gegeben.<ref>{{Literatur|Autor= John David Jackson|Titel= Klassische Elektrodynamik|Auflage= 3|Verlag= De Gruyter|Ort= Berlin • New York|Datum= 2002|ISBN= 3-11-016502-3|Seiten= 766}}</ref> Es bezeichnen | |||
* <math>\vec n</math> den [[Einheitsvektor]] zwischen Beobachtungspunkt und Ort des Teilchens, | |||
* <math>R</math> den Abstand zwischen Beobachtungspunkt und Ort des Teilchens | |||
* <math>q</math> die elektrische Ladung des Teilchens, | |||
* <math>\vec \beta</math> die Geschwindigkeit in Einheiten der Lichtgeschwindigkeit, | |||
* <math>\gamma</math> den [[Lorentzfaktor]] <math>\gamma = (1-\beta^2)^{-1/2}</math>, | |||
* <math>c</math> die Lichtgeschwindigkeit, | |||
* <math>\varepsilon_0</math> die [[Elektrische Feldkonstante]] und | |||
* das Subskript <math>\text{ret}</math>, dass die Argumente zur [[Retardiertes Potential|retardierten]] Zeit <math>t' = t - R/c</math> auszuwerten sind. | |||
In dieser Form sind die elektrischen und magnetischen Felder in ein Geschwindigkeitsfeld, das nur von der momentanen Geschwindigkeit abhängt, und ein Beschleunigungsfeld unterteilt. Das Beschleunigungfeld hat dabei ein Abhängigkeit proportional zu <math>1/R</math>, sodass seine [[Leistungsdichte]] im Unendlichen nicht verschwindet. Es ist daher ein Strahlungsfeld. | |||
Die Komponente des [[Poynting-Vektor]]s <math>\vec S</math> dieses Strahlungsfeldes in Beobachtungsrichtung, was der Leistungsdichte entspricht, ist | |||
:<math>\left[\vec n \cdot \vec S\right]_\text{ret} = \frac{q^2}{16 \pi^2 \varepsilon_0 c} \left[\frac{1}{R^2} \left|\frac{\vec n \times [(\vec n - \vec \beta) \times \dot \vec \beta]}{(1-\vec \beta \cdot \vec n)^3}\right|^2\right]_\text{ret}</math> | |||
entsprechend der abgestrahlten Leistung zur retardierten Zeit <math>t'</math> pro Raumwinkelemenent <math>\mathrm d\Omega</math> | |||
:<math>\frac{\mathrm dP(t')}{\mathrm d\Omega} = \frac{q^2}{16 \pi^2 \varepsilon_0 c} \frac{\left|\vec n \times [(\vec n - \vec \beta)\times \dot \vec \beta]\right|^2}{(1 - \vec n \cdot \vec \beta)^5}</math>. | |||
Dies ist die relativistische Verallgemeinerung der [[Larmor-Formel]] für den Energieverlust beschleunigter Ladungen.<ref>{{Literatur|Autor= John David Jackson|Titel= Klassische Elektrodynamik|Auflage= 3|Verlag= De Gruyter|Ort= Berlin • New York|Datum= 2002|ISBN= 3-11-016502-3|Seiten= 771-772}}</ref> | |||
Das Frequenzspektrum der Bremsstrahlung ergibt sich nach einer [[Fourier-Transformation]] der abgestrahlten Gesamtenergie zu<ref>{{Literatur|Autor= John David Jackson|Titel= Klassische Elektrodynamik|Auflage= 3|Verlag= De Gruyter|Ort= Berlin • New York|Datum= 2002|ISBN= 3-11-016502-3|Seiten= 779}}</ref> | |||
:<math>\frac{\mathrm d^2 I}{\mathrm d\omega\, \mathrm d\Omega} = \frac{q^2}{16 \pi^3 \varepsilon_0 c} \left|\int_{-\infty}^\infty \mathrm dt\, \frac{\vec n \times [(\vec n - \vec \beta)\times \dot \vec \beta]}{(1 - \vec \beta \cdot \vec n)^2} e^{\mathrm i \omega(t - \vec n \cdot \vec x(t)/c)}\right|^2 = \frac{q^2}{16\pi^3 \varepsilon_0 c} \omega^2 \left|\int_{-\infty}^\infty \mathrm dt\, \vec n \times (\vec n \times \vec \beta) e^{\mathrm i \omega(t - \vec n \cdot \vec x(t)/c)}\right|^2</math> | |||
mit | |||
* der [[Intensität (Physik)|Intensität]] <math>I</math>, | |||
* der [[Winkelfrequenz]] <math>\omega</math> und | |||
* der [[Bahnkurve]] des geladenen Teilchens <math>\vec x(t)</math>. | |||
== Spektralverteilung der Bremsstrahlung einer Röntgenröhre == | == Spektralverteilung der Bremsstrahlung einer Röntgenröhre == | ||
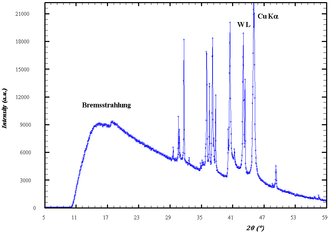
[[Datei:Tube Cu LiF.PNG| | [[Datei:Tube Cu LiF.PNG|mini|Spektrum von Röntgenstrahlung einer Kupferanode. Die horizontale Achse zeigt den [[Ablenkwinkel]] nach [[Bragg-Gleichung|Bragg-Reflexion]] an einem [[LiF]]-Kristall]] | ||
Zu kurzen [[Wellenlänge]]n hin hat das Spektrum eine Grenzwellenlänge, die der kinetischen Energie der Elektronen entspricht, d. h. die gesamte kinetische Energie der Elektronen wird in Röntgenstrahlung umgewandelt. Diese Grenzwellenlänge hängt nur von der durchlaufenen [[Beschleunigungsspannung]] ([[Anodenspannung]]) ab, sie ist unabhängig vom Anodenmaterial; die Form des Spektrums hängt ab von der [[Geschwindigkeitsverteilung]] der Elektronen und dem verwendeten Metall. | Zu kurzen [[Wellenlänge]]n hin hat das Spektrum eine Grenzwellenlänge, die der kinetischen Energie der Elektronen entspricht, d. h. die gesamte kinetische Energie der Elektronen wird in Röntgenstrahlung umgewandelt. Diese Grenzwellenlänge hängt nur von der durchlaufenen [[Beschleunigungsspannung]] ([[Anodenspannung]]) ab, sie ist unabhängig vom Anodenmaterial; die Form des Spektrums hängt ab von der [[Geschwindigkeitsverteilung]] der Elektronen und dem verwendeten Metall. | ||
| Zeile 20: | Zeile 51: | ||
:<math>\begin{alignat}{2} | :<math>\begin{alignat}{2} | ||
& E_\text{kinetisch} && = E_\text{Photon}\\ | & E_\text{kinetisch} && = E_\text{Photon}\\ | ||
\Leftrightarrow & e \cdot U && = h \cdot f | \Leftrightarrow\quad & e \cdot U && = h \cdot f | ||
\end{alignat}</math> | \end{alignat}</math> | ||
| Zeile 37: | Zeile 68: | ||
:<math>\Rightarrow {\lambda_\mathrm{min}} = \frac{h \cdot c}{e \cdot U}</math> | :<math>\Rightarrow {\lambda_\mathrm{min}} = \frac{h \cdot c}{e \cdot U}</math> | ||
Durch Einsetzen der [[Naturkonstante]]n ''h'' ''c'' und ''e'' ergibt sich die zugeschnittene [[Größengleichung]]: | Durch Einsetzen der [[Naturkonstante]]n ''h,'' ''c'' und ''e'' ergibt sich die zugeschnittene [[Größengleichung]]: | ||
:<math>{\lambda_\mathrm{min}} = \frac{1{,}24\cdot 10^{-6}\,\mathrm{V}\cdot \mathrm{m}}{U}</math> <ref>Universität Ulm: [http://www.uni-ulm.de/fileadmin/website_uni_ulm/nawi.inst.251/Didactics/quantenchemie/html/RontgenF.html Röntgenbremsstrahlung]</ref> | :<math>{\lambda_\mathrm{min}} = \frac{1{,}24\cdot 10^{-6}\,\mathrm{V}\cdot \mathrm{m}}{U}</math> <ref>Universität Ulm: [http://www.uni-ulm.de/fileadmin/website_uni_ulm/nawi.inst.251/Didactics/quantenchemie/html/RontgenF.html Röntgenbremsstrahlung]</ref> | ||
Die untere Grenzwellenlänge <math>\lambda_\mathrm{min}</math> hängt also nur von der Beschleunigungsspannung <math>U</math> ab; | Die untere Grenzwellenlänge <math>\lambda_\mathrm{min}</math> hängt also nur von der Beschleunigungsspannung <math>U</math> ab; | ||
bei einer Beschleunigungsspannung von 25 kV beträgt sie 0,05 [[Nanometer|nm]]. Diese Strahlung vermag bereits normales [[Glas]] und dünne [[Aluminium]]<nowiki/>platten zu durchdringen. Daher müssen bei Farb-[[Bildröhre]]n, die mit Beschleunigungsspannungen von 25 bis 27 kV arbeiten (Schwarzweiß-Bildröhre: ca. 18 kV), Maßnahmen zum [[Strahlenschutz]] getroffen werden. Man verwendet daher [[ | bei einer Beschleunigungsspannung von 25 kV beträgt sie 0,05 [[Nanometer|nm]]. Diese Strahlung vermag bereits normales [[Glas]] und dünne [[Aluminium]]<nowiki/>platten zu durchdringen. Daher müssen bei Farb-[[Bildröhre]]n, die mit Beschleunigungsspannungen von 25 bis 27 kV arbeiten (Schwarzweiß-Bildröhre: ca. 18 kV), Maßnahmen zum [[Strahlenschutz]] getroffen werden. Man verwendet daher [[Bleiglas]] für den Kolben. | ||
Die kontinuierliche | Die kontinuierliche Energieverteilung der Bremsstrahlung <math>\tfrac{\mathrm dE}{\mathrm df}</math>, wenn Elektronen in ein Material eintreten, ist nach Kramers<ref>XCIII. On the theory of X-ray absorption and of the continuous X-ray spectrum H. A. Kramers in Philos. Mag. Ser. 6, 46 (1923) Pages 836–871 {{DOI|10.1080/14786442308565244}}</ref> über die Frequenz linear. Nach Umrechnung in die Wellenlängendarstellung ergibt sich: | ||
:<math>\frac{\mathrm dE}{\mathrm d\lambda} = KIZ \frac{h}{c} \left(\frac{\lambda}{\lambda_\mathrm{min}} - 1 \right) \frac{1}{\lambda^3} </math> | |||
mit | |||
: der Kramersschen Konstante <math>K</math>, | |||
: dem Elektronenstrom <math>I</math> und | |||
: der [[Ordnungszahl]] der Atome des Materials <math>Z</math>. | |||
Bezogen auf die spektrale Anzahldichte der Photonen <math>\tfrac{\mathrm dn}{\mathrm d\lambda}</math> ergibt sich | |||
:<math>\frac{\mathrm dn}{\mathrm d\lambda} = KIZ \left(\frac{\lambda}{\lambda_\mathrm{min}}-1\right) \frac{1}{\lambda^2}.</math> | |||
Bei realen Spektren von Röntgenemissionen wird die entstehende Bremsstrahlung durch verschiedene Effekte überlagert. Hinzu kommt insbesondere die [[Charakteristische Röntgenstrahlung|charakteristische Strahlung]] (Peaks in der Abb.), die ein [[Emissionsspektrum]] der Atome des Materials darstellt, sowie dessen [[Absorptionsbande]]n, da die Bremsstrahlung unter der Materialoberfläche entsteht. | Bei realen Spektren von Röntgenemissionen wird die entstehende Bremsstrahlung durch verschiedene Effekte überlagert. Hinzu kommt insbesondere die [[Charakteristische Röntgenstrahlung|charakteristische Strahlung]] (Peaks in der Abb.), die ein [[Emissionsspektrum]] der Atome des Materials darstellt, sowie dessen [[Absorptionsbande]]n, da die Bremsstrahlung unter der Materialoberfläche entsteht. | ||
== Elektron-Elektron-Bremsstrahlung == | == Elektron-Elektron-Bremsstrahlung == | ||
Ein für kleine Ordnungszahlen <math>Z</math> wichtiger Prozess ist die [[Streuung (Physik)|Streuung]] freier Elektronen an den [[Schalenmodell (Atomphysik)|Schalen]]<nowiki/>elektronen eines Atoms oder Moleküls.<ref>{{Literatur |Autor=Frédéric Tessier, Iwan Kawrakow |Jahr=2008 |Titel=Calculation of the electron–electron bremsstrahlung cross-section in the field of atomic electrons |Sammelwerk=Nuclear Instruments and Methods in Physics Research Section B |Band=266 |Nummer=4 |Seiten=625–634 |DOI=10.1016/j.nimb.2007.11.063}}</ref> Da diese Elektron-Elektron-Bremsstrahlung eine Funktion von <math>Z</math>, die Elektron-Kern-Bremsstrahlung jedoch eine Funktion von <math>Z^2</math> ist, kann die Elektron-Elektron-Bremsstrahlung für [[Metalle]] vernachlässigt werden. Für Luft jedoch spielt sie eine wichtige Rolle bei der Erzeugung [[Terrestrischer Gammablitz|terrestrischer Gammablitze]].<ref> | Ein für kleine Ordnungszahlen <math>Z</math> wichtiger Prozess ist die [[Streuung (Physik)|Streuung]] freier Elektronen an den [[Schalenmodell (Atomphysik)|Schalen]]<nowiki/>elektronen eines Atoms oder Moleküls.<ref>{{Literatur |Autor=Frédéric Tessier, Iwan Kawrakow |Jahr=2008 |Titel=Calculation of the electron–electron bremsstrahlung cross-section in the field of atomic electrons |Sammelwerk=Nuclear Instruments and Methods in Physics Research Section B |Band=266 |Nummer=4 |Seiten=625–634 |DOI=10.1016/j.nimb.2007.11.063}}</ref> Da diese Elektron-Elektron-Bremsstrahlung eine Funktion von <math>Z</math>, die Elektron-Kern-Bremsstrahlung jedoch eine Funktion von <math>Z^2</math> ist, kann die Elektron-Elektron-Bremsstrahlung für [[Metalle]] vernachlässigt werden. Für Luft jedoch spielt sie eine wichtige Rolle bei der Erzeugung [[Terrestrischer Gammablitz|terrestrischer Gammablitze]].<ref>Köhn, C., Ebert, U. The importance of electron-electron Bremsstrahlung for terrestrial gamma-ray flashes, electron beams and electron-positron beams J. Phys. D.: Appl. Phys. as Fast Track Communication (2014), vol. 47, 252001. ([http://iopscience.iop.org/0022-3727/47/25/252001 abstract])</ref> | ||
== Weblinks == | == Weblinks == | ||
{{Commonscat}} | |||
{{Wiktionary}} | |||
* desy.de: [http://www.desy.de/pr-info/Roentgen-light/roentgenstrahlung/roentgenstrahlung8.html Röntgen light - Bremsstrahlung] | * desy.de: [http://www.desy.de/pr-info/Roentgen-light/roentgenstrahlung/roentgenstrahlung8.html Röntgen light - Bremsstrahlung] | ||
* [http://xfelinfo.desy.de/de/artikel.roentgenlicht-spektrum/2/index.html Spektrum der Röntgenbremsstrahlung] | * [http://xfelinfo.desy.de/de/artikel.roentgenlicht-spektrum/2/index.html Spektrum der Röntgenbremsstrahlung] | ||
== Einzelnachweise == | |||
<references /><br />{{Normdaten|TYP=s|GND=4142023-8|LCCN=sh/85/16730|NDL=00570284}} | |||
[[Kategorie:Elektrodynamik]] | [[Kategorie:Elektrodynamik]] | ||
[[Kategorie:Strahlung]] | [[Kategorie:Strahlung]] | ||
Aktuelle Version vom 13. Oktober 2021, 09:40 Uhr
Bremsstrahlung ist die elektromagnetische Strahlung, die durch die Beschleunigung eines elektrisch geladenen Teilchens, z. B. eines Elektrons, entsteht. Entgegen der Namensgebung tritt diese Strahlung nicht nur dann auf, wenn sich der Betrag der Geschwindigkeit verringert, sondern auch, wenn er sich vergrößert oder die Geschwindigkeit nur ihre Richtung verändert. Von Bremsstrahlung im engeren Sinne spricht man, wenn Teilchen in Materie gebremst werden.
Vom Standpunkt der Quantenelektrodynamik aus lässt sich die Erzeugung von Bremsstrahlung erklären, dass jede Wechselwirkung von geladenen Teilchen mit der Emission oder Absorption von Photonen, den Quanten der elektromagnetischen Strahlung, verbunden ist.
Auftreten bzw. Anwendung
Bei Teilchenbeschleunigern (vor allem bei Synchrotronen) und bei Speicherringen wird bei der Ablenkung geladener Teilchen durch ein Magnetfeld Bremsstrahlung frei, die in diesen Zusammenhängen Synchrotronstrahlung genannt wird.
Der Effekt der Bremsstrahlung wird in Röntgenröhren zur Erzeugung von Röntgenstrahlung verwendet. Dabei schießt man Elektronen mit einer kinetischen Energie ab 30 keV auf eine Metallplatte, die häufig aus Wolfram besteht. Ein kleiner Teil der beim Abbremsen frei werdenden Energie wird in Röntgenstrahlung mit einem kontinuierlichen Spektrum (einem Röntgenkontinuum) umgewandelt.
Bremsstrahlung kann außerdem die Entwicklung und Morphologie elektrischer Entladungen beeinflussen[1] sowie hochenergetische terrestrische Gammablitze und Positronen erzeugen.[2]
Physik der Bremsstrahlung
Das elektromagnetische Feld bewegter Ladungen wird durch die Liénard-Wiechert-Potentiale beschrieben. Danach sind das elektrische Feld $ {\vec {E}} $ und das magnetische Feld $ {\vec {B}} $ durch
- $ {\begin{aligned}{\vec {E}}({\vec {x}},t)&={\frac {q}{4\pi \varepsilon _{0}}}\left[{\frac {{\vec {n}}-{\vec {\beta }}}{\gamma ^{2}(1-{\vec {\beta }}\cdot {\vec {n}})^{3}R^{2}}}\right]_{\text{ret}}+{\frac {q}{4\pi \varepsilon _{0}c}}\left[{\frac {{\vec {n}}\times [({\vec {n}}-{\vec {\beta }})\times {\dot {\vec {\beta }}}]}{(1-{\vec {\beta }}\cdot {\vec {n}})^{3}R}}\right]_{\text{ret}}\\{\vec {B}}({\vec {x}},t)&={\frac {1}{c}}\left[{\vec {n}}\times {\vec {E}}\right]_{\text{ret}}\end{aligned}} $
gegeben.[3] Es bezeichnen
- $ {\vec {n}} $ den Einheitsvektor zwischen Beobachtungspunkt und Ort des Teilchens,
- $ R $ den Abstand zwischen Beobachtungspunkt und Ort des Teilchens
- $ q $ die elektrische Ladung des Teilchens,
- $ {\vec {\beta }} $ die Geschwindigkeit in Einheiten der Lichtgeschwindigkeit,
- $ \gamma $ den Lorentzfaktor $ \gamma =(1-\beta ^{2})^{-1/2} $,
- $ c $ die Lichtgeschwindigkeit,
- $ \varepsilon _{0} $ die Elektrische Feldkonstante und
- das Subskript $ {\text{ret}} $, dass die Argumente zur retardierten Zeit $ t'=t-R/c $ auszuwerten sind.
In dieser Form sind die elektrischen und magnetischen Felder in ein Geschwindigkeitsfeld, das nur von der momentanen Geschwindigkeit abhängt, und ein Beschleunigungsfeld unterteilt. Das Beschleunigungfeld hat dabei ein Abhängigkeit proportional zu $ 1/R $, sodass seine Leistungsdichte im Unendlichen nicht verschwindet. Es ist daher ein Strahlungsfeld.
Die Komponente des Poynting-Vektors $ {\vec {S}} $ dieses Strahlungsfeldes in Beobachtungsrichtung, was der Leistungsdichte entspricht, ist
- $ \left[{\vec {n}}\cdot {\vec {S}}\right]_{\text{ret}}={\frac {q^{2}}{16\pi ^{2}\varepsilon _{0}c}}\left[{\frac {1}{R^{2}}}\left|{\frac {{\vec {n}}\times [({\vec {n}}-{\vec {\beta }})\times {\dot {\vec {\beta }}}]}{(1-{\vec {\beta }}\cdot {\vec {n}})^{3}}}\right|^{2}\right]_{\text{ret}} $
entsprechend der abgestrahlten Leistung zur retardierten Zeit $ t' $ pro Raumwinkelemenent $ \mathrm {d} \Omega $
- $ {\frac {\mathrm {d} P(t')}{\mathrm {d} \Omega }}={\frac {q^{2}}{16\pi ^{2}\varepsilon _{0}c}}{\frac {\left|{\vec {n}}\times [({\vec {n}}-{\vec {\beta }})\times {\dot {\vec {\beta }}}]\right|^{2}}{(1-{\vec {n}}\cdot {\vec {\beta }})^{5}}} $.
Dies ist die relativistische Verallgemeinerung der Larmor-Formel für den Energieverlust beschleunigter Ladungen.[4]
Das Frequenzspektrum der Bremsstrahlung ergibt sich nach einer Fourier-Transformation der abgestrahlten Gesamtenergie zu[5]
- $ {\frac {\mathrm {d} ^{2}I}{\mathrm {d} \omega \,\mathrm {d} \Omega }}={\frac {q^{2}}{16\pi ^{3}\varepsilon _{0}c}}\left|\int _{-\infty }^{\infty }\mathrm {d} t\,{\frac {{\vec {n}}\times [({\vec {n}}-{\vec {\beta }})\times {\dot {\vec {\beta }}}]}{(1-{\vec {\beta }}\cdot {\vec {n}})^{2}}}e^{\mathrm {i} \omega (t-{\vec {n}}\cdot {\vec {x}}(t)/c)}\right|^{2}={\frac {q^{2}}{16\pi ^{3}\varepsilon _{0}c}}\omega ^{2}\left|\int _{-\infty }^{\infty }\mathrm {d} t\,{\vec {n}}\times ({\vec {n}}\times {\vec {\beta }})e^{\mathrm {i} \omega (t-{\vec {n}}\cdot {\vec {x}}(t)/c)}\right|^{2} $
mit
- der Intensität $ I $,
- der Winkelfrequenz $ \omega $ und
- der Bahnkurve des geladenen Teilchens $ {\vec {x}}(t) $.
Spektralverteilung der Bremsstrahlung einer Röntgenröhre
Zu kurzen Wellenlängen hin hat das Spektrum eine Grenzwellenlänge, die der kinetischen Energie der Elektronen entspricht, d. h. die gesamte kinetische Energie der Elektronen wird in Röntgenstrahlung umgewandelt. Diese Grenzwellenlänge hängt nur von der durchlaufenen Beschleunigungsspannung (Anodenspannung) ab, sie ist unabhängig vom Anodenmaterial; die Form des Spektrums hängt ab von der Geschwindigkeitsverteilung der Elektronen und dem verwendeten Metall.
Die kürzestmögliche Wellenlänge $ \lambda $ (siehe Duane-Hunt-Gesetz) tritt auf, wenn die gesamte kinetische Energie des Elektrons in die Strahlungsenergie eines einzigen Photons umgewandelt wird:
- $ {\begin{alignedat}{2}&E_{\text{kinetisch}}&&=E_{\text{Photon}}\\\Leftrightarrow \quad &e\cdot U&&=h\cdot f\end{alignedat}} $
mit
- der Elementarladung $ e $ des Elektrons
- der Beschleunigungs- bzw. Anodenspannung $ U $ der Röntgenröhre
- dem Planckschen Wirkungsquantum $ h $
- der Frequenz $ f $.
Mit
- $ f={\frac {c}{\lambda }} $ (c für die Lichtgeschwindigkeit)
folgt
- $ \Rightarrow {\lambda _{\mathrm {min} }}={\frac {h\cdot c}{e\cdot U}} $
Durch Einsetzen der Naturkonstanten h, c und e ergibt sich die zugeschnittene Größengleichung:
- $ {\lambda _{\mathrm {min} }}={\frac {1{,}24\cdot 10^{-6}\,\mathrm {V} \cdot \mathrm {m} }{U}} $ [6]
Die untere Grenzwellenlänge $ \lambda _{\mathrm {min} } $ hängt also nur von der Beschleunigungsspannung $ U $ ab; bei einer Beschleunigungsspannung von 25 kV beträgt sie 0,05 nm. Diese Strahlung vermag bereits normales Glas und dünne Aluminiumplatten zu durchdringen. Daher müssen bei Farb-Bildröhren, die mit Beschleunigungsspannungen von 25 bis 27 kV arbeiten (Schwarzweiß-Bildröhre: ca. 18 kV), Maßnahmen zum Strahlenschutz getroffen werden. Man verwendet daher Bleiglas für den Kolben.
Die kontinuierliche Energieverteilung der Bremsstrahlung $ {\tfrac {\mathrm {d} E}{\mathrm {d} f}} $, wenn Elektronen in ein Material eintreten, ist nach Kramers[7] über die Frequenz linear. Nach Umrechnung in die Wellenlängendarstellung ergibt sich:
- $ {\frac {\mathrm {d} E}{\mathrm {d} \lambda }}=KIZ{\frac {h}{c}}\left({\frac {\lambda }{\lambda _{\mathrm {min} }}}-1\right){\frac {1}{\lambda ^{3}}} $
mit
- der Kramersschen Konstante $ K $,
- dem Elektronenstrom $ I $ und
- der Ordnungszahl der Atome des Materials $ Z $.
Bezogen auf die spektrale Anzahldichte der Photonen $ {\tfrac {\mathrm {d} n}{\mathrm {d} \lambda }} $ ergibt sich
- $ {\frac {\mathrm {d} n}{\mathrm {d} \lambda }}=KIZ\left({\frac {\lambda }{\lambda _{\mathrm {min} }}}-1\right){\frac {1}{\lambda ^{2}}}. $
Bei realen Spektren von Röntgenemissionen wird die entstehende Bremsstrahlung durch verschiedene Effekte überlagert. Hinzu kommt insbesondere die charakteristische Strahlung (Peaks in der Abb.), die ein Emissionsspektrum der Atome des Materials darstellt, sowie dessen Absorptionsbanden, da die Bremsstrahlung unter der Materialoberfläche entsteht.
Elektron-Elektron-Bremsstrahlung
Ein für kleine Ordnungszahlen $ Z $ wichtiger Prozess ist die Streuung freier Elektronen an den Schalenelektronen eines Atoms oder Moleküls.[8] Da diese Elektron-Elektron-Bremsstrahlung eine Funktion von $ Z $, die Elektron-Kern-Bremsstrahlung jedoch eine Funktion von $ Z^{2} $ ist, kann die Elektron-Elektron-Bremsstrahlung für Metalle vernachlässigt werden. Für Luft jedoch spielt sie eine wichtige Rolle bei der Erzeugung terrestrischer Gammablitze.[9]
Weblinks
Einzelnachweise
- ↑ Köhn, C., Chanrion, O., Neubert, T. The influence of bremsstrahlung on electric discharge streamers in N2, O2 gas mixtures Plasma Sources Sci. Technol. (2017), vol. 26, 015006. doi:10.1088/0963-0252/26/1/015006.
- ↑ Köhn, C., Ebert, U. Calculation of beams of positrons, neutrons, and protons associated with terrestrial gamma ray flashes Journal Geophys. Res. (2015), vol. 120, pp. 1620–1635. doi:10.1002/2014JD022229.
- ↑ John David Jackson: Klassische Elektrodynamik. 3. Auflage. De Gruyter, Berlin • New York 2002, ISBN 3-11-016502-3, S. 766.
- ↑ John David Jackson: Klassische Elektrodynamik. 3. Auflage. De Gruyter, Berlin • New York 2002, ISBN 3-11-016502-3, S. 771–772.
- ↑ John David Jackson: Klassische Elektrodynamik. 3. Auflage. De Gruyter, Berlin • New York 2002, ISBN 3-11-016502-3, S. 779.
- ↑ Universität Ulm: Röntgenbremsstrahlung
- ↑ XCIII. On the theory of X-ray absorption and of the continuous X-ray spectrum H. A. Kramers in Philos. Mag. Ser. 6, 46 (1923) Pages 836–871 doi:10.1080/14786442308565244
- ↑ Frédéric Tessier, Iwan Kawrakow: Calculation of the electron–electron bremsstrahlung cross-section in the field of atomic electrons. In: Nuclear Instruments and Methods in Physics Research Section B. Band 266, Nr. 4, 2008, S. 625–634, doi:10.1016/j.nimb.2007.11.063.
- ↑ Köhn, C., Ebert, U. The importance of electron-electron Bremsstrahlung for terrestrial gamma-ray flashes, electron beams and electron-positron beams J. Phys. D.: Appl. Phys. as Fast Track Communication (2014), vol. 47, 252001. (abstract)