Stefan-Boltzmann-Gesetz: Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Thermodynamik
- Atomphysik
- Strahlung
- Ludwig Boltzmann
imported>Boehm K (typog) |
imported>Kuebi K (Änderungen von 80.152.57.58 (Diskussion) auf die letzte Version von Aka zurückgesetzt) |
||
| Zeile 1: | Zeile 1: | ||
Das '''Stefan-Boltzmann-Gesetz''' ist ein [[physikalisches Gesetz]], das die thermisch abgestrahlte [[Leistung (Physik)|Leistung]] eines [[Schwarzer Körper|idealen Schwarzen Körpers]] in Abhängigkeit von seiner [[Temperatur]] angibt. Es ist benannt nach den Physikern [[Josef Stefan]] und [[Ludwig Boltzmann]]. | Das '''Stefan-Boltzmann-Gesetz''' ist ein [[physikalisches Gesetz]], das die thermisch abgestrahlte [[Leistung (Physik)|Leistung]] eines [[Schwarzer Körper|idealen Schwarzen Körpers]] in Abhängigkeit von seiner [[Temperatur]] angibt. Es ist benannt nach den Physikern [[Josef Stefan]] und [[Ludwig Boltzmann]]. | ||
== | == Überblick == | ||
Jeder Körper, dessen Temperatur über dem [[Absoluter Nullpunkt|absoluten Nullpunkt]] liegt, gibt [[Wärmestrahlung]] an seine Umgebung ab. Ein Schwarzer Körper ist ein idealisierter Körper, der alle auf ihn treffende Strahlung vollständig absorbieren kann (Absorptionsgrad = 1). Nach dem [[Kirchhoffsches Strahlungsgesetz|kirchhoffschen Strahlungsgesetz]] erreicht daher auch sein [[Emissionsgrad]] ''ε'' den Wert 1, und er sendet die bei der betreffenden Temperatur maximal mögliche thermische Leistung aus. Das Stefan-Boltzmann-Gesetz gibt an, welche Strahlungsleistung <math>P</math> ein Schwarzer Körper der Fläche <math>A</math> und der [[Absolute Temperatur|absoluten Temperatur]] <math>T</math> aussendet. Es lautet | [[Datei:Emissive Power.svg|mini|Anstieg der emittierten Strahlungsleistung über die Temperatur]] | ||
Jeder Körper, dessen Temperatur über dem [[Absoluter Nullpunkt|absoluten Nullpunkt]] liegt, gibt [[Wärmestrahlung]] an seine Umgebung ab. Ein Schwarzer Körper ist ein idealisierter Körper, der alle auf ihn treffende Strahlung vollständig absorbieren kann (Absorptionsgrad = 1). Nach dem [[Kirchhoffsches Strahlungsgesetz|kirchhoffschen Strahlungsgesetz]] erreicht daher auch sein [[Emissionsgrad]] ''ε'' den Wert 1, und er sendet die bei der betreffenden Temperatur maximal mögliche thermische Leistung aus. Das Stefan-Boltzmann-Gesetz gibt an, welche [[Strahlungsleistung]] <math>P</math> ein Schwarzer Körper der Fläche <math>A</math> und der [[Absolute Temperatur|absoluten Temperatur]] <math>T</math> aussendet. Es lautet in drei Raumdimensionen | |||
: <math>P = \sigma \cdot A\cdot T^4</math> | : <math>P = \sigma \cdot A\cdot T^4</math> | ||
mit der | mit der [[Stefan-Boltzmann-Konstante]]n <math>\sigma</math>. Die Strahlungsleistung eines Schwarzen Körpers ist also proportional zur vierten [[Potenz (Mathematik)|Potenz]] seiner absoluten Temperatur: Eine Verdopplung der Temperatur bewirkt, dass die abgestrahlte Leistung um den Faktor 16 ansteigt. Dieses Gesetz wird deshalb auch als „Boltzmannsches T-hoch-vier-Gesetz“ bezeichnet. | ||
Der Wert | Der Wert der Stefan-Boltzmann-Konstanten beträgt<ref>{{Internetquelle |url=https://physics.nist.gov/cgi-bin/cuu/Value?sigma |hrsg=National Institute of Standards and Technology |titel=Stefan-Boltzmann constant |zugriff=2019-07-30}} Wert für <math>\sigma</math>.</ref> | ||
: <math>\sigma = \frac{2\pi^5 k_\mathrm{B}^4}{15h^3c^2} = | : <math>\sigma = \frac{2\pi^5 k_\mathrm{B}^4}{15h^3c^2} = 5{,}670\,374\,419... \,\cdot 10^{-8} \, \mathrm{\frac{W}{m^2 K^4}}.</math> | ||
Er ist exakt bekannt, weil das [[Internationales Einheitensystem|Internationale Einheitensystem]] seit der [[Internationales Einheitensystem#Neudefinition2019|Revision von 2019]] dadurch definiert ist, dass u. a. den Konstanten der [[Lichtgeschwindigkeit]] <math>c</math>, dem [[Plancksches Wirkungsquantum|Planckschen Wirkungsquantum]] <math>h</math> und der [[Boltzmann-Konstante]] <math>k_\mathrm{B}</math> ein fester Wert zugewiesen wurde.<ref name="CGPM-26-1" /> In dieser Form gilt das Stefan-Boltzmann-Gesetz für dreidimensionale Körper, d. h., die Ausdehnung des Körpers in alle Raumrichtungen ist sehr viel größer als die Wellenlängen der elektromagnetischen Strahlung, deren Beitrag zur Gesamtleistung nicht vernachlässigbar klein ist. Falls eine der Dimensionen des Körpers sehr viel kleiner ist als die relevanten Wellenlängen, handelt es sich um einen zweidimensionalen Körper (Fläche), falls zwei Dimensionen sehr viel kleiner sind, um einen eindimensionalen (Stab). In diesen Fällen können sich die Wellen im Körper nicht in drei Dimensionen ausbreiten, und somit ist die gesamte innere Energie <math>U</math> kleiner. Entsprechend ist auch die abgestrahlte Leistung von der Dimension abhängig. | |||
Es gilt: | |||
:<math>U_3 = a_3 V T^4</math> | |||
mit | |||
:<math>a_3 = \frac{4\sigma}{c} \approx 7{,}566 \cdot 10^{-16} \mathrm{\frac{J}{m^3 K^4}}</math> | |||
sowie | |||
: <math>U_2 = a_2 A T^3\cdot </math> | |||
: <math> | |||
mit | mit | ||
: <math> | : <math>a_2 = \frac{4\pi k_\mathrm{B}^3 \zeta(3)}{h^2c^2}\approx 1{,}007 \cdot 10^{-18}\,\mathrm{\frac{J}{m^2 K^3}}</math>, | ||
und | wobei <math>\zeta(s)</math> die [[Riemannsche Zeta-Funktion]] ist und <math>\zeta(3)</math> auch als [[Apéry-Konstante]] bezeichnet wird, und | ||
: <math> | : <math>U_1 = a_1 L T^2</math> | ||
mit | mit | ||
: <math> | : <math>a_1 = \frac{\pi^2 k_\mathrm{B}^2}{3hc} \approx 3{,}157\cdot 10^{-21}\,\mathrm{\frac{J}{K^2 m}}</math> | ||
Die abgestrahlte Energie eines Schwarzen Körpers ist im Allgemeinen also proportional zur <math>(n+1)</math>-ten Potenz seiner absoluten Temperatur, wobei <math>n</math> die Dimension des Körpers bezeichnet. | |||
== Herleitung aus der Thermodynamik == | == Herleitung aus der Thermodynamik == | ||
Das Stefan-Boltzmann-Gesetz wurde im Jahr 1879 von Josef Stefan experimentell entdeckt.<ref>J. Stefan: ''Über die Beziehung zwischen der Wärmestrahlung und der Temperatur.'' In: ''Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der kaiserlichen Akademie der Wissenschaften.'' Bd. 79 (Wien 1879), S. 391–428.</ref> Boltzmann leitete 1884 dieses Strahlungsgesetz aus Gesetzen der Thermodynamik und der klassischen [[Maxwell-Gleichungen|Maxwellschen Elektrodynamik]] ab.<ref>L. Boltzmann: ''Ableitung des Stefan’schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie.'' In: ''Annalen der Physik und Chemie.'' Bd. 22, 1884, S. 291–294 [[doi:10.1002/andp.18842580616]].</ref> Ausgehend von einer der [[Fundamentalgleichung|thermodynamischen Grundgleichungen]] für ein [[abgeschlossenes System]] im [[Thermodynamisches Gleichgewicht|thermodynamischen Gleichgewicht]]: | Das Stefan-Boltzmann-Gesetz wurde im Jahr 1879 von Josef Stefan experimentell entdeckt.<ref>J. Stefan: ''Über die Beziehung zwischen der Wärmestrahlung und der Temperatur.'' In: ''Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der kaiserlichen Akademie der Wissenschaften.'' Bd. 79 (Wien 1879), S. 391–428.</ref> Boltzmann leitete 1884 dieses Strahlungsgesetz aus Gesetzen der Thermodynamik und der klassischen [[Maxwell-Gleichungen|Maxwellschen Elektrodynamik]] ab.<ref>L. Boltzmann: ''Ableitung des Stefan’schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie.'' In: ''Annalen der Physik und Chemie.'' Bd. 22, 1884, S. 291–294 [[doi:10.1002/andp.18842580616]].</ref> Ausgehend von einer der [[Fundamentalgleichung|thermodynamischen Grundgleichungen]] für ein [[Abgeschlossenes System (Thermodynamik)|abgeschlossenes System]] im [[Thermodynamisches Gleichgewicht|thermodynamischen Gleichgewicht]]: | ||
: <math>T \mathrm dS = \mathrm dU + p \mathrm dV</math> | : <math>T \mathrm dS = \mathrm dU + p \mathrm dV</math> | ||
findet man unter Beachtung der [[Totales Differential#Integrabilitätsbedingung|Integrabilitätsbedingung]] den Ausdruck | findet man unter Beachtung der [[Totales Differential#Integrabilitätsbedingung|Integrabilitätsbedingung]] den Ausdruck | ||
| Zeile 72: | Zeile 60: | ||
Da der Schwarze Körper grundsätzlich ein diffuser Strahler und seine spektrale Strahldichte daher richtungsunabhängig ist, ergibt das Integral, ausgeführt über den Halbraum, den Wert <math>\pi</math>. Für die Integration über die Frequenzen ist | Da der Schwarze Körper grundsätzlich ein diffuser Strahler und seine spektrale Strahldichte daher richtungsunabhängig ist, ergibt das Integral, ausgeführt über den Halbraum, den Wert <math>\pi</math>. Für die Integration über die Frequenzen ist | ||
: <math>\int_{0}^{\infty} \frac{x^3}{e^{x}-1} \, \mathrm{d}x = \frac{\pi^4}{15}</math> | : <math>\int_{0}^{\infty} \frac{x^3}{e^{x}-1} \, \mathrm{d}x = \frac{\pi^4}{15}</math> | ||
zu beachten. Integriert man die so erhaltene spezifische Ausstrahlung <math>M^o(T)</math> noch über die abstrahlende Fläche, erhält man das Stefan-Boltzmann-Gesetz in der oben angegebenen Form. | zu beachten. Integriert man die so erhaltene [[spezifische Ausstrahlung]] <math>M^o(T)</math> noch über die abstrahlende Fläche, erhält man das Stefan-Boltzmann-Gesetz in der oben angegebenen Form. | ||
Für den ein- und zweidimensionalen Fall sind hier zwei andere Integrale zu lösen. Es gilt:<ref>''[[:en:Special:PermanentLink/293273084#Appendix|Planck’s law (Appendix)]]'' in der englischsprachigen Wikipedia, 30. Mai 2009 <small>(as edited by DumZiBoT at 08:56)</small>.</ref> | Für den ein- und zweidimensionalen Fall sind hier zwei andere Integrale zu lösen. Es gilt:<ref>''[[:en:Special:PermanentLink/293273084#Appendix|Planck’s law (Appendix)]]'' in der englischsprachigen Wikipedia, 30. Mai 2009 <small>(as edited by DumZiBoT at 08:56)</small>.</ref> | ||
: <math>\int_{0}^{\infty}\frac{x^{n}}{e^x-1}\,dx = \zeta(n+1) \Gamma{\left(n+1\right)} = \zeta(n+1)\cdot n!</math> | : <math>\int_{0}^{\infty}\frac{x^{n}}{e^x-1}\,dx = \zeta(n+1) \Gamma{\left(n+1\right)} = \zeta(n+1)\cdot n!</math> | ||
Somit folgt für <math>n=1</math> | |||
Hierbei ist <math>\zeta(\cdot)</math> die [[Riemannsche Zetafunktion]] und <math>\Gamma(\cdot)</math> die [[Gammafunktion]]. Somit folgt für <math>n=1</math> | |||
: <math>\int_{0}^{\infty} \frac{x}{e^{x}-1} \, \mathrm{d}x = \zeta(2)\cdot 1! = \frac{\pi^2}{6}</math> | : <math>\int_{0}^{\infty} \frac{x}{e^{x}-1} \, \mathrm{d}x = \zeta(2)\cdot 1! = \frac{\pi^2}{6}</math> | ||
und daraus folgt für <math>n=2</math> | und daraus folgt für <math>n=2</math> | ||
| Zeile 83: | Zeile 72: | ||
== Nicht-Schwarze Strahler == | == Nicht-Schwarze Strahler == | ||
Das Stefan-Boltzmann-Gesetz gilt in der obigen Form nur für Schwarze Strahler. | Das Stefan-Boltzmann-Gesetz gilt in der obigen Form nur für Schwarze Strahler. Wenn ein Nicht-Schwarzer Strahler gegeben ist, der richtungsunabhängig strahlt (sogenannter [[Lambert-Strahler]]) und dessen [[Emissionsgrad]] <math>\varepsilon(T)</math> für alle Frequenzen denselben Wert hat (sogenannter [[Grauer Körper]]), dann ist | ||
: <math>P = \varepsilon(T) \cdot \sigma \cdot A \cdot T^4</math> | : <math>P = \varepsilon(T) \cdot \sigma \cdot A \cdot T^4</math> | ||
die von diesem abgegebene Strahlungsleistung. Dabei ist der Emissionsgrad <math>\varepsilon(T)</math> der gewichtete gemittelte Emissionsgrad über alle Wellenlängen und die Wichtungsfunktion ist die Schwarzkörperenergieverteilung. <math>\varepsilon(T)</math> streut [[Emissionsgrad#Tabellen|materialabhängig]] zwischen 0,012 und 0,98. Ist der Emissionsgrad wellenlängenabhängig, so ändert sich die Strahlungsverteilung nicht nur wegen der Änderung der Planck-Verteilung. Durch diese ''zusätzliche'' Temperaturabhängigkeit ist die gesamte Strahlungsleistung nicht mehr streng proportional zur vierten Potenz der absoluten Temperatur. | die von diesem abgegebene Strahlungsleistung. Dabei ist der Emissionsgrad <math>\varepsilon(T)</math> der gewichtete gemittelte Emissionsgrad über alle Wellenlängen und die Wichtungsfunktion ist die Schwarzkörperenergieverteilung. <math>\varepsilon(T)</math> streut [[Emissionsgrad#Tabellen|materialabhängig]] zwischen 0,012 und 0,98. Ist der Emissionsgrad wellenlängenabhängig, so ändert sich die Strahlungsverteilung nicht nur wegen der Änderung der Planck-Verteilung. Durch diese ''zusätzliche'' Temperaturabhängigkeit ist die gesamte Strahlungsleistung nicht mehr streng proportional zur vierten Potenz der absoluten Temperatur. | ||
| Zeile 91: | Zeile 80: | ||
== Beispiel == | == Beispiel == | ||
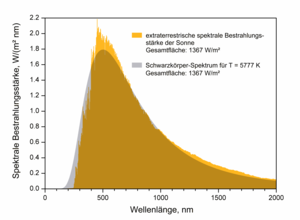
[[Datei:EffectiveTemperature 300dpi.png|mini|Vergleich des Abstrahlverhaltens der Sonne und eines Schwarzen Körpers. Die effektive Temperatur der Sonne beträgt 5777 K.]] | [[Datei:EffectiveTemperature 300dpi.png|mini|Vergleich des Abstrahlverhaltens der Sonne und eines Schwarzen Körpers. Die effektive Temperatur der Sonne beträgt 5777 K.]] | ||
Außerhalb der Erdatmosphäre im Abstand Sonne-Erde empfängt eine zur Sonne ausgerichtete Fläche eine Bestrahlungsstärke von | Außerhalb der Erdatmosphäre im Abstand Sonne-Erde empfängt eine zur Sonne ausgerichtete Fläche eine Bestrahlungsstärke von <math>S =1361 \, \mathrm{W/m^2}</math> ([[Solarkonstante]]). Man bestimme die Temperatur <math>T</math> der Sonnenoberfläche unter der Annahme, dass die Sonne in hinreichender Näherung ein Schwarzer Körper sei. Der Sonnenradius beträgt <math>R = 6{,}963 \cdot 10^8 \mathrm m</math>, der mittlere Abstand zwischen Erde und Sonne ist <math>D = 1{,}496 \cdot 10^{11} \mathrm m</math>. | ||
Die von der Sonnenoberfläche abgegebene Strahlungsleistung | Die von der Sonnenoberfläche abgegebene Strahlungsleistung <math>P</math> durchdringt eine konzentrisch um die Sonne gelegte Kugelschale des Radius <math>D</math> mit der Bestrahlungsstärke <math>S</math>, beträgt also insgesamt <math>P = 4\pi D^2 \cdot S = 3{,}845 \cdot 10^{26} \mathrm W</math> ([[Leuchtkraft]] der Sonne). Nach dem Stefan-Boltzmann-Gesetz beträgt die Temperatur der abstrahlenden Oberfläche | ||
: <math>T = \sqrt[4]{\frac{P}{\sigma A}} = \sqrt[4]{\frac{S \cdot 4 \pi D^2}{\sigma \cdot 4 \pi R^2}} = \sqrt[4]{\frac{S \cdot D^2}{\sigma \cdot R^2}} = \sqrt[4]{\frac{1\, | :<math>T = \sqrt[4]{\frac{P}{\sigma A}} = \sqrt[4]{\frac{S \cdot 4 \pi D^2}{\sigma \cdot 4 \pi R^2}} = \sqrt[4]{\frac{S \cdot D^2}{\sigma \cdot R^2}} = \sqrt[4]{\frac{1\,361 \cdot 2{,}238 \cdot 10^{22}}{5{,}670 \cdot 10^{-8} \, \cdot \, 4{,}844 \cdot 10^{17}}} \; \mathrm{K} = 5\,771 \, \mathrm{K}.</math> | ||
Die so bestimmte Temperatur der Sonnenoberfläche heißt ''Effektivtemperatur.'' Es ist die Temperatur, die ein gleich großer Schwarzer Körper haben müsste, um dieselbe Strahlungsleistung abzugeben wie die Sonne. | Die so bestimmte Temperatur der Sonnenoberfläche heißt ''Effektivtemperatur.'' Es ist die Temperatur, die ein gleich großer Schwarzer Körper haben müsste, um dieselbe Strahlungsleistung abzugeben wie die Sonne. | ||
== Siehe auch == | == Siehe auch == | ||
Das Stefan-Boltzmann-Gesetz macht eine Aussage über die von einem Schwarzen Körper auf allen Frequenzen insgesamt abgegebene Strahlungsleistung. Die Aufteilung auf einzelne Frequenzen bzw. Wellenlängen wird vom [[Plancksches Strahlungsgesetz| | Das Stefan-Boltzmann-Gesetz macht eine Aussage über die von einem Schwarzen Körper auf allen Frequenzen insgesamt abgegebene Strahlungsleistung. Die Aufteilung auf einzelne Frequenzen bzw. Wellenlängen wird vom [[Plancksches Strahlungsgesetz|Planckschen<!-- klein! Neue Rechtschreibung --> Strahlungsgesetz]] beschrieben. | ||
Das [[Wiensches Verschiebungsgesetz| | Das [[Wiensches Verschiebungsgesetz|Wiensche Verschiebungsgesetz]] verbindet die Temperatur eines Schwarzen Körpers mit der am stärksten abgestrahlten Wellenlänge. | ||
== Weblinks == | == Weblinks == | ||
| Zeile 106: | Zeile 95: | ||
== Einzelnachweise == | == Einzelnachweise == | ||
<references /> | <references> | ||
<ref name="CGPM-26-1"> | |||
{{Internetquelle | |||
|url=https://www.bipm.org/en/committees/cg/cgpm/26-2018/resolution-1 | |||
|titel=Resolution 1 of the 26th CGPM. On the revision of the International System of Units (SI) | |||
|titelerg= | |||
|werk= | |||
|hrsg=[[Internationales Büro für Maß und Gewicht|Bureau International des Poids et Mesures]] | |||
|datum=2018 | |||
|sprache=en | |||
|abruf=2021-04-14 | |||
}} | |||
</ref> | |||
</references> | |||
[[Kategorie:Thermodynamik]] | [[Kategorie:Thermodynamik]] | ||
[[Kategorie:Atomphysik]] | [[Kategorie:Atomphysik]] | ||
[[Kategorie:Strahlung]] | [[Kategorie:Strahlung]] | ||
[[Kategorie:Ludwig Boltzmann]] | |||
Aktuelle Version vom 21. Januar 2022, 07:49 Uhr
Das Stefan-Boltzmann-Gesetz ist ein physikalisches Gesetz, das die thermisch abgestrahlte Leistung eines idealen Schwarzen Körpers in Abhängigkeit von seiner Temperatur angibt. Es ist benannt nach den Physikern Josef Stefan und Ludwig Boltzmann.
Überblick
Jeder Körper, dessen Temperatur über dem absoluten Nullpunkt liegt, gibt Wärmestrahlung an seine Umgebung ab. Ein Schwarzer Körper ist ein idealisierter Körper, der alle auf ihn treffende Strahlung vollständig absorbieren kann (Absorptionsgrad = 1). Nach dem kirchhoffschen Strahlungsgesetz erreicht daher auch sein Emissionsgrad ε den Wert 1, und er sendet die bei der betreffenden Temperatur maximal mögliche thermische Leistung aus. Das Stefan-Boltzmann-Gesetz gibt an, welche Strahlungsleistung $ P $ ein Schwarzer Körper der Fläche $ A $ und der absoluten Temperatur $ T $ aussendet. Es lautet in drei Raumdimensionen
- $ P=\sigma \cdot A\cdot T^{4} $
mit der Stefan-Boltzmann-Konstanten $ \sigma $. Die Strahlungsleistung eines Schwarzen Körpers ist also proportional zur vierten Potenz seiner absoluten Temperatur: Eine Verdopplung der Temperatur bewirkt, dass die abgestrahlte Leistung um den Faktor 16 ansteigt. Dieses Gesetz wird deshalb auch als „Boltzmannsches T-hoch-vier-Gesetz“ bezeichnet.
Der Wert der Stefan-Boltzmann-Konstanten beträgt[1]
- $ \sigma ={\frac {2\pi ^{5}k_{\mathrm {B} }^{4}}{15h^{3}c^{2}}}=5{,}670\,374\,419...\,\cdot 10^{-8}\,\mathrm {\frac {W}{m^{2}K^{4}}} . $
Er ist exakt bekannt, weil das Internationale Einheitensystem seit der Revision von 2019 dadurch definiert ist, dass u. a. den Konstanten der Lichtgeschwindigkeit $ c $, dem Planckschen Wirkungsquantum $ h $ und der Boltzmann-Konstante $ k_{\mathrm {B} } $ ein fester Wert zugewiesen wurde.[2] In dieser Form gilt das Stefan-Boltzmann-Gesetz für dreidimensionale Körper, d. h., die Ausdehnung des Körpers in alle Raumrichtungen ist sehr viel größer als die Wellenlängen der elektromagnetischen Strahlung, deren Beitrag zur Gesamtleistung nicht vernachlässigbar klein ist. Falls eine der Dimensionen des Körpers sehr viel kleiner ist als die relevanten Wellenlängen, handelt es sich um einen zweidimensionalen Körper (Fläche), falls zwei Dimensionen sehr viel kleiner sind, um einen eindimensionalen (Stab). In diesen Fällen können sich die Wellen im Körper nicht in drei Dimensionen ausbreiten, und somit ist die gesamte innere Energie $ U $ kleiner. Entsprechend ist auch die abgestrahlte Leistung von der Dimension abhängig.
Es gilt:
- $ U_{3}=a_{3}VT^{4} $
mit
- $ a_{3}={\frac {4\sigma }{c}}\approx 7{,}566\cdot 10^{-16}\mathrm {\frac {J}{m^{3}K^{4}}} $
sowie
- $ U_{2}=a_{2}AT^{3}\cdot $
mit
- $ a_{2}={\frac {4\pi k_{\mathrm {B} }^{3}\zeta (3)}{h^{2}c^{2}}}\approx 1{,}007\cdot 10^{-18}\,\mathrm {\frac {J}{m^{2}K^{3}}} $,
wobei $ \zeta (s) $ die Riemannsche Zeta-Funktion ist und $ \zeta (3) $ auch als Apéry-Konstante bezeichnet wird, und
- $ U_{1}=a_{1}LT^{2} $
mit
- $ a_{1}={\frac {\pi ^{2}k_{\mathrm {B} }^{2}}{3hc}}\approx 3{,}157\cdot 10^{-21}\,\mathrm {\frac {J}{K^{2}m}} $
Die abgestrahlte Energie eines Schwarzen Körpers ist im Allgemeinen also proportional zur $ (n+1) $-ten Potenz seiner absoluten Temperatur, wobei $ n $ die Dimension des Körpers bezeichnet.
Herleitung aus der Thermodynamik
Das Stefan-Boltzmann-Gesetz wurde im Jahr 1879 von Josef Stefan experimentell entdeckt.[3] Boltzmann leitete 1884 dieses Strahlungsgesetz aus Gesetzen der Thermodynamik und der klassischen Maxwellschen Elektrodynamik ab.[4] Ausgehend von einer der thermodynamischen Grundgleichungen für ein abgeschlossenes System im thermodynamischen Gleichgewicht:
- $ T\mathrm {d} S=\mathrm {d} U+p\mathrm {d} V $
findet man unter Beachtung der Integrabilitätsbedingung den Ausdruck
- $ \left({\frac {\partial U}{\partial V}}\right)_{T}=T\left({\frac {\partial p}{\partial T}}\right)_{V}-p. $
mit
- $ S $: Entropie
- $ U $: innere Energie
- $ V $: Volumen
- $ p $: Druck
- $ T $: Temperatur.
Maxwell zeigte bereits 1873, dass sich der Strahlungsdruck als
- $ p={\frac {1}{3}}u $
schreiben lässt. $ u $ ist hierbei die Energiedichte der elektromagnetischen Strahlung. Adolfo Bartoli konnte ferner im Jahre 1876 die Existenz eines Strahlungsdruckes thermodynamisch rechtfertigen, indem er darlegte, dass im Falle der Nichtexistenz der zweite Hauptsatz der Thermodynamik verletzt würde. Der Vorfaktor 1/3 folgt allerdings nur aus elektrodynamischen Betrachtungen.
Setzt man diesen Ausdruck für $ p $ in die vorhergehende Beziehung ein und berücksichtigt, dass die gesamte Energie in einem Volumen sich als $ U=u\cdot V $ schreiben lässt, so folgt nach Integration
- $ u=a\cdot T^{4} $
bzw. für die gesamte Energie
- $ U=aT^{4}V. $
Die Integrationskonstante $ a $ bleibt jedoch zunächst unbestimmt. Sie musste durch Experimente, wie zum Beispiel jene von Joseph Stefan, bestimmt werden. Dass es sich dabei um eine aus anderen Naturkonstanten zusammengesetzte Größe handelt, zeigte sich erst in der Quantenmechanik. Im Jahre 1900, also 21 Jahre nach dem Stefan-Boltzmann-Gesetz, entdeckte Max Planck das nach ihm benannte plancksche Strahlungsgesetz, aus dem das Stefan-Boltzmann-Gesetz einfach durch Integration über alle Richtungen und Wellenlängen folgt. Das plancksche Strahlungsgesetz konnte mit der Einführung des Wirkungsquantums $ h $ auch erstmals die Stefan-Boltzmann-Konstante auf fundamentale Naturkonstanten zurückführen.
In älterer Literatur wird die Größe $ a $ ebenfalls als Stefan-Boltzman-Konstante bezeichnet.[5] Mit der durch das CODATA unter diesem Namen geführten Konstanten $ \sigma $ steht $ a $, die sogenannte Strahlungskonstante, allerdings über
- $ a={\frac {4\sigma }{c}}={\frac {8\pi ^{5}k_{\mathrm {B} }^{4}}{15c^{3}h^{3}}} $
in Beziehung; in Zahlen ausgedrückt:
- $ a=7{,}567\cdot 10^{-16}\;{\text{J}}\,{\text{m}}^{-3}\,{\text{K}}^{-4} $
Herleitung aus der Quantenmechanik
Zur Herleitung geht man von der spektralen Strahlungsdichte eines Schwarzen Körpers aus und integriert diese sowohl über den gesamten Halbraum, in den das betrachtete Flächenelement abstrahlt, als auch über alle Frequenzen:
- $ M^{o}(T)=\int \limits _{\nu =0}^{\infty }\int \limits _{\text{Halbraum}}{\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\left({\frac {h\nu }{k_{\mathrm {B} }T}}\right)}-1}}\,\cos \beta \,\sin \beta \,\mathrm {d} \beta \,\mathrm {d} \varphi \,\mathrm {d} \nu $
Gemäß dem Lambertschen Gesetz berücksichtigt dabei der Kosinusfaktor den Umstand, dass bei Abstrahlung in eine beliebige durch die Winkel $ \beta $ und $ \varphi $ gegebene Richtung nur die auf dieser Richtung senkrecht stehende Projektion $ \cos \beta \,\mathrm {d} A $ der Fläche $ \mathrm {d} A $ als effektive Strahlfläche auftritt. Der Term $ \sin \beta \,\mathrm {d} \beta \,\mathrm {d} \varphi $ ist ein Raumwinkelelement.
Da der Schwarze Körper grundsätzlich ein diffuser Strahler und seine spektrale Strahldichte daher richtungsunabhängig ist, ergibt das Integral, ausgeführt über den Halbraum, den Wert $ \pi $. Für die Integration über die Frequenzen ist
- $ \int _{0}^{\infty }{\frac {x^{3}}{e^{x}-1}}\,\mathrm {d} x={\frac {\pi ^{4}}{15}} $
zu beachten. Integriert man die so erhaltene spezifische Ausstrahlung $ M^{o}(T) $ noch über die abstrahlende Fläche, erhält man das Stefan-Boltzmann-Gesetz in der oben angegebenen Form.
Für den ein- und zweidimensionalen Fall sind hier zwei andere Integrale zu lösen. Es gilt:[6]
- $ \int _{0}^{\infty }{\frac {x^{n}}{e^{x}-1}}\,dx=\zeta (n+1)\Gamma {\left(n+1\right)}=\zeta (n+1)\cdot n! $
Hierbei ist $ \zeta (\cdot ) $ die Riemannsche Zetafunktion und $ \Gamma (\cdot ) $ die Gammafunktion. Somit folgt für $ n=1 $
- $ \int _{0}^{\infty }{\frac {x}{e^{x}-1}}\,\mathrm {d} x=\zeta (2)\cdot 1!={\frac {\pi ^{2}}{6}} $
und daraus folgt für $ n=2 $
- $ \int _{0}^{\infty }{\frac {x^{2}}{e^{x}-1}}\,\mathrm {d} x=\zeta (3)\cdot 2!=2\cdot \zeta (3)\approx 2{,}40411. $
Diese Integrale werden z. B. durch geschickte Umformung oder mit Hilfe der Funktionentheorie gelöst.[7]
Nicht-Schwarze Strahler
Das Stefan-Boltzmann-Gesetz gilt in der obigen Form nur für Schwarze Strahler. Wenn ein Nicht-Schwarzer Strahler gegeben ist, der richtungsunabhängig strahlt (sogenannter Lambert-Strahler) und dessen Emissionsgrad $ \varepsilon (T) $ für alle Frequenzen denselben Wert hat (sogenannter Grauer Körper), dann ist
- $ P=\varepsilon (T)\cdot \sigma \cdot A\cdot T^{4} $
die von diesem abgegebene Strahlungsleistung. Dabei ist der Emissionsgrad $ \varepsilon (T) $ der gewichtete gemittelte Emissionsgrad über alle Wellenlängen und die Wichtungsfunktion ist die Schwarzkörperenergieverteilung. $ \varepsilon (T) $ streut materialabhängig zwischen 0,012 und 0,98. Ist der Emissionsgrad wellenlängenabhängig, so ändert sich die Strahlungsverteilung nicht nur wegen der Änderung der Planck-Verteilung. Durch diese zusätzliche Temperaturabhängigkeit ist die gesamte Strahlungsleistung nicht mehr streng proportional zur vierten Potenz der absoluten Temperatur.
Für einen Strahler, bei dem die Richtungsunabhängigkeit oder die Frequenzunabhängigkeit der Emission nicht gegeben ist, muss zur Bestimmung des hemisphärischen Gesamtemissionsgrads ε(T) das Integral individuell unter Zugrundelegung der betreffenden Gesetzmäßigkeiten berechnet werden. Viele Körper weichen nur wenig vom idealen Lambert-Strahler ab; wenn der Emissionsgrad in dem Frequenzbereich, in dem der Körper einen merklichen Anteil seiner Strahlungsleistung abgibt, nur wenig variiert, lässt sich das Stefan-Boltzmann-Gesetz zumindest näherungsweise anwenden.
Beispiel
Außerhalb der Erdatmosphäre im Abstand Sonne-Erde empfängt eine zur Sonne ausgerichtete Fläche eine Bestrahlungsstärke von $ S=1361\,\mathrm {W/m^{2}} $ (Solarkonstante). Man bestimme die Temperatur $ T $ der Sonnenoberfläche unter der Annahme, dass die Sonne in hinreichender Näherung ein Schwarzer Körper sei. Der Sonnenradius beträgt $ R=6{,}963\cdot 10^{8}\mathrm {m} $, der mittlere Abstand zwischen Erde und Sonne ist $ D=1{,}496\cdot 10^{11}\mathrm {m} $.
Die von der Sonnenoberfläche abgegebene Strahlungsleistung $ P $ durchdringt eine konzentrisch um die Sonne gelegte Kugelschale des Radius $ D $ mit der Bestrahlungsstärke $ S $, beträgt also insgesamt $ P=4\pi D^{2}\cdot S=3{,}845\cdot 10^{26}\mathrm {W} $ (Leuchtkraft der Sonne). Nach dem Stefan-Boltzmann-Gesetz beträgt die Temperatur der abstrahlenden Oberfläche
- $ T={\sqrt[{4}]{\frac {P}{\sigma A}}}={\sqrt[{4}]{\frac {S\cdot 4\pi D^{2}}{\sigma \cdot 4\pi R^{2}}}}={\sqrt[{4}]{\frac {S\cdot D^{2}}{\sigma \cdot R^{2}}}}={\sqrt[{4}]{\frac {1\,361\cdot 2{,}238\cdot 10^{22}}{5{,}670\cdot 10^{-8}\,\cdot \,4{,}844\cdot 10^{17}}}}\;\mathrm {K} =5\,771\,\mathrm {K} . $
Die so bestimmte Temperatur der Sonnenoberfläche heißt Effektivtemperatur. Es ist die Temperatur, die ein gleich großer Schwarzer Körper haben müsste, um dieselbe Strahlungsleistung abzugeben wie die Sonne.
Siehe auch
Das Stefan-Boltzmann-Gesetz macht eine Aussage über die von einem Schwarzen Körper auf allen Frequenzen insgesamt abgegebene Strahlungsleistung. Die Aufteilung auf einzelne Frequenzen bzw. Wellenlängen wird vom Planckschen Strahlungsgesetz beschrieben.
Das Wiensche Verschiebungsgesetz verbindet die Temperatur eines Schwarzen Körpers mit der am stärksten abgestrahlten Wellenlänge.
Weblinks
Einzelnachweise
- ↑ Stefan-Boltzmann constant. National Institute of Standards and Technology, abgerufen am 30. Juli 2019. Wert für $ \sigma $.
- ↑ Resolution 1 of the 26th CGPM. On the revision of the International System of Units (SI). Bureau International des Poids et Mesures, 2018, abgerufen am 14. April 2021 (Lua-Fehler in Modul:Multilingual, Zeile 149: attempt to index field 'data' (a nil value)).
- ↑ J. Stefan: Über die Beziehung zwischen der Wärmestrahlung und der Temperatur. In: Sitzungsberichte der mathematisch-naturwissenschaftlichen Classe der kaiserlichen Akademie der Wissenschaften. Bd. 79 (Wien 1879), S. 391–428.
- ↑ L. Boltzmann: Ableitung des Stefan’schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie. In: Annalen der Physik und Chemie. Bd. 22, 1884, S. 291–294 doi:10.1002/andp.18842580616.
- ↑ I. P. Bazarov: Thermodynamik. Dt. Verl. der Wiss., Berlin 1964, S. 130.
- ↑ Planck’s law (Appendix) in der englischsprachigen Wikipedia, 30. Mai 2009 (as edited by DumZiBoT at 08:56).
- ↑ Stefan–Boltzmann law (Appendix) in der englischsprachigen Wikipedia, 30. März 2009 (as edited by JAnDbot at 17:59).