Interferenz (Physik): Unterschied zwischen den Versionen
- Seiten mit Skriptfehlern
- Quantenphysik
- Wellenoptik
- Akustik
- Wellenlehre
imported>Acky69 K (→Anschauliche Erklärung: zus. Link) |
imported>ZabesBot K (Bot: Räume alte Interwikilinks auf) |
||
| Zeile 5: | Zeile 5: | ||
'''Interferenz''' ([[Latein|lat.]] ''{{lang|la|inter}}'' ‚zwischen‘ und ''{{lang|la|ferire}}'' über [[Altfranzösische Sprache|altfrz.]] ''{{lang|fro|s’entreferir}}'' ‚sich gegenseitig schlagen‘)<ref>{{Literatur |Autor=R. E. Allen, H. W. Fowler, F. G. Fowler |Titel=The Concise Oxford dictionary of current English. |Verlag=Clarendon Press/Oxford University Press |Ort=Oxford/New York |Datum=1990 |ISBN=0-19-861200-1}}</ref> beschreibt die Änderung der Amplitude bei der Überlagerung von zwei oder mehr [[Welle]]n nach dem [[Superposition (Physik)|Superpositionsprinzip]] – also die vorzeichenrichtige Addition ihrer [[Auslenkung]]en (nicht der [[Intensität (Physik)|Intensitäten]]) während ihrer Durchdringung. Interferenz tritt bei allen Arten von Wellen auf, also bei [[Schall]]-, [[Licht]]-, [[Materiewelle]]n usw. | '''Interferenz''' ([[Latein|lat.]] ''{{lang|la|inter}}'' ‚zwischen‘ und ''{{lang|la|ferire}}'' über [[Altfranzösische Sprache|altfrz.]] ''{{lang|fro|s’entreferir}}'' ‚sich gegenseitig schlagen‘)<ref>{{Literatur |Autor=R. E. Allen, H. W. Fowler, F. G. Fowler |Titel=The Concise Oxford dictionary of current English. |Verlag=Clarendon Press/Oxford University Press |Ort=Oxford/New York |Datum=1990 |ISBN=0-19-861200-1}}</ref> beschreibt die Änderung der Amplitude bei der Überlagerung von zwei oder mehr [[Welle]]n nach dem [[Superposition (Physik)|Superpositionsprinzip]] – also die vorzeichenrichtige Addition ihrer [[Auslenkung]]en (nicht der [[Intensität (Physik)|Intensitäten]]) während ihrer Durchdringung. Interferenz tritt bei allen Arten von Wellen auf, also bei [[Schall]]-, [[Licht]]-, [[Materiewelle]]n usw. | ||
An Orten, wo sich die Wellen dabei gegenseitig auslöschen, herrscht '''destruktive Interferenz'''. An Orten, wo sie sich verstärken, herrscht '''konstruktive Interferenz'''. Ein Zeichen für das Auftreten von Interferenz zweier Wellenfelder sind abwechselnde Maxima und Minima der Intensität, wo jedes Wellenfeld für sich eine gleichmäßige Intensität hatte. Diese Folge von konstruktiver und destruktiver Interferenz wird als '''Interferenzmuster''' bezeichnet. Ein bekanntes Beispiel sind die hellen bzw. dunklen Streifen beim [[Doppelspaltversuch]]. Das Auftreten von Interferenz im physikalischen Experiment gilt als Nachweis für die Wellennatur der untersuchten Strahlung. | |||
== Grundlagen und Voraussetzungen == | == Grundlagen und Voraussetzungen == | ||
| Zeile 12: | Zeile 12: | ||
Das Wellenfeld, das aus der Interferenz zweier (oder mehrerer) Wellen entsteht, kann nur dann zeitlich stabil sein, wenn diese Wellen untereinander eine (zeitlich) feste Phasenbeziehung aufweisen. Man spricht dann von [[Kohärenz (Physik)|kohärenten]] Wellen. Sind die Wellen nicht [[monochromatisch]], bestehen also aus einer ganzen Reihe von Frequenzanteilen, so definiert man eine Kohärenzzeit, die beschreibt, wie die Wellen maximal gegeneinander verschoben sein dürfen, um noch ein stabiles Wellenfeld zu erzeugen. Diese Kohärenzzeit (oder die daraus abgeleitete [[Kohärenzlänge]]) ist ein wichtiges Maß für physikalische Lichtquellen. | Das Wellenfeld, das aus der Interferenz zweier (oder mehrerer) Wellen entsteht, kann nur dann zeitlich stabil sein, wenn diese Wellen untereinander eine (zeitlich) feste Phasenbeziehung aufweisen. Man spricht dann von [[Kohärenz (Physik)|kohärenten]] Wellen. Sind die Wellen nicht [[monochromatisch]], bestehen also aus einer ganzen Reihe von Frequenzanteilen, so definiert man eine Kohärenzzeit, die beschreibt, wie die Wellen maximal gegeneinander verschoben sein dürfen, um noch ein stabiles Wellenfeld zu erzeugen. Diese Kohärenzzeit (oder die daraus abgeleitete [[Kohärenzlänge]]) ist ein wichtiges Maß für physikalische Lichtquellen. | ||
=== Destruktive Interferenz === | |||
Zwei Wellen löschen sich gegenseitig völlig aus, wenn ihre Auslenkungen am betrachteten Ort und Zeitpunkt entgegengesetzt gleich sind. Damit das an diesem Ort für längere Zeit so bleibt, müssen harmonische (d. h. sinusförmige) Wellen gleiche Frequenz haben und um eine halbe Schwingungsperiode bzw. eine halbe Wellenlänge gegeneinander versetzt sein (siehe [[Phasenverschiebung]] bzw. [[Gangunterschied]]). Bei transversalen Wellen (z. B. [[Licht]]) müssen die Auslenkungen in derselben Ebene liegen, bei komplexen Wellen (z. B. quantenmechanische [[Wellenfunktion]]) muss die komplexe Phase der [[Amplitude]] übereinstimmen. | |||
=== Polarisation === | === Polarisation === | ||
| Zeile 23: | Zeile 26: | ||
=== Interferenz zweier Wellen gleicher Frequenz und Amplitude, aber unterschiedlicher Phase === | === Interferenz zweier Wellen gleicher Frequenz und Amplitude, aber unterschiedlicher Phase === | ||
Die Überlagerung zweier Wellen gleicher Frequenz und Amplitude lässt sich anhand der trigonometrischen Additionstheoreme berechnen. Werden die beiden Wellen <math>f_1(t)</math> und <math>f_2(t)</math> mit der gemeinsamen Frequenz <math>\omega</math>, der Amplitude <math>a</math> und den Phasen ''<math>\varphi_1</math>'' und ''<math>\varphi_2</math>'' durch | Die Überlagerung zweier Wellen gleicher Frequenz und Amplitude lässt sich anhand der trigonometrischen [[Additionstheoreme (Trigonometrie)|Additionstheoreme]] berechnen. Werden die beiden Wellen <math>f_1(t)</math> und <math>f_2(t)</math> mit der gemeinsamen Frequenz <math>\omega</math>, der Amplitude <math>a</math> und den Phasen ''<math>\varphi_1</math>'' und ''<math>\varphi_2</math>'' durch | ||
:<math>f_1 (t) = a \cdot \sin(\omega \cdot t + \varphi_1) </math> und <math>f_2 (t) = a \cdot \sin(\omega \cdot t + \varphi_2)\, | :<math>f_1 (t) = a \cdot \sin(\omega \cdot t + \varphi_1) </math> und <math>f_2 (t) = a \cdot \sin(\omega \cdot t + \varphi_2)\, | ||
</math> | </math> | ||
beschrieben, so ergibt sich für die resultierende Überlagerung der Wellen | beschrieben, so ergibt sich für die resultierende Überlagerung der Wellen | ||
:<math> | :<math> | ||
f_1 (t) + f_2 (t) = a \left( \sin(\omega t + \varphi_1) + \sin(\omega t + \varphi_2) \right) = 2a \cos\left(\frac{\varphi_1 - \varphi_2}{2}\right) \sin\left(\omega t + \frac{\varphi_1 + \varphi_2}{2}\right)\, | f_1 (t) + f_2 (t) = a \left( \sin(\omega t + \varphi_1) + \sin(\omega t + \varphi_2) \right) = 2a \cos\left(\frac{\varphi_1 - \varphi_2}{2}\right) \sin\left(\omega t + \frac{\varphi_1 + \varphi_2}{2}\right)\, | ||
| Zeile 33: | Zeile 38: | ||
d. h., es entsteht eine Welle derselben Frequenz, deren Amplitude von der Differenz der Phasen der beiden ursprünglichen Wellen abhängt und deren Phase das Mittel der Phasen der ursprünglichen Wellen ist. | d. h., es entsteht eine Welle derselben Frequenz, deren Amplitude von der Differenz der Phasen der beiden ursprünglichen Wellen abhängt und deren Phase das Mittel der Phasen der ursprünglichen Wellen ist. | ||
Für gleiche Phasen der Wellen (<math>\varphi_1 = \varphi_2</math>) wird der Cosinus Eins. Es ergibt sich eine Amplitude von <math>2a</math>, d. h., die Amplitude verdoppelt sich gegenüber den Ausgangsamplituden, was konstruktiver Interferenz entspricht. Für eine Phasendifferenz von 180° | |||
Für gleiche Phasen der Wellen (<math>\varphi_1 = \varphi_2</math>) wird der Cosinus Eins. Es ergibt sich eine Amplitude von <math>2a</math>, d. h., die Amplitude verdoppelt sich gegenüber den Ausgangsamplituden, was konstruktiver Interferenz entspricht. | |||
Für eine Phasendifferenz von 180° (<math>\varphi_1 = \varphi_2 + \pi</math>) wird der Cosinus Null, d. h., die resultierende Welle verschwindet. Dieses entspricht ''destruktiver Interferenz''. | |||
=== Interferenz zweier Wellen gleicher Frequenz aber unterschiedlicher Amplitude und Phase === | === Interferenz zweier Wellen gleicher Frequenz aber unterschiedlicher Amplitude und Phase === | ||
| Zeile 59: | Zeile 67: | ||
[[Datei:Shallow water waves.gif|rechts|Die Reflexion an den Seitenwänden führt zu konstruktiver Interferenz mit besonders hoher Amplitude.]] | [[Datei:Shallow water waves.gif|rechts|Die Reflexion an den Seitenwänden führt zu konstruktiver Interferenz mit besonders hoher Amplitude.]] | ||
--> | --> | ||
Die Abbildung | Die Abbildung 1 zeigt die Interferenz von zwei kreisförmigen Wellengruppen gleicher Wellenlänge und Amplitude. Die Kreuze markieren die Lage der Quellen, die Kreise die Maxima der jeweiligen Teilwelle. An weißen Stellen tritt konstruktive Interferenz, in positiver Richtung, an schwarzen konstruktive Interferenz, in negativer Richtung, auf. An den grauen Stellen herrscht destruktive Interferenz. Es ist zu erkennen, dass die Minima auf einer Hyperbelschar liegen, deren Brennpunkte identisch den Quellorten der Wellen sind. Man spricht deshalb bei zwei Punktquellen von einer hyperbolischen Interferenz. Die [[Hyperbel (Mathematik)|Hyperbel]] ist dabei die Kurve aller Punkte, die zu den zwei Quellorten die Laufzeitdifferenz <math>t = \tfrac{\lambda}2</math> haben. Der Scheitelpunktabstand <math>\!\ 2 a</math> entspricht der Laufzeitdifferenz <math>\!\ 2 a = (T_1 - T_2) v</math>, wenn <math>\!\ T_1</math> und <math>\!\ T_2</math> den Zeitbezug der beiden speisenden Zeitfunktionen darstellen und <math>v</math> die mediale Ausbreitungsgeschwindigkeit darstellt. | ||
In der | In der Abbildung 2 wird die Veränderung des Interferenzbildes in Abhängigkeit von der Wellenlänge (nimmt von oben nach unten zu) und in Abhängigkeit vom Abstand der Quellen (nimmt von links nach rechts zu) demonstriert. In den dunklen Bereichen (um die ''Interferenzminima'') liegt ''destruktive'' und in den hellen ''(Maxima)'' ''konstruktive Interferenz'' vor. | ||
<!-- | <!-- | ||
Die Animation rechts zeigt, wie es durch Reflexion an den Seitenwänden an der oberen Ecke immer wieder zu konstruktiver Interferenz mit besonders hoher Amplitude kommt. | Die Animation rechts zeigt, wie es durch Reflexion an den Seitenwänden an der oberen Ecke immer wieder zu konstruktiver Interferenz mit besonders hoher Amplitude kommt. | ||
| Zeile 67: | Zeile 75: | ||
<gallery class="centered"> | <gallery class="centered"> | ||
Interferenz.jpg|Simulierte Interferenz von zwei kreisförmigen Wellengruppen gleicher Wellenlänge und Amplitude | Datei:Interferenz.jpg|Abbildung 1: Simulierte Interferenz von zwei kreisförmigen Wellengruppen gleicher Wellenlänge und Amplitude | ||
Datei:Wavepanel.png|Abbildung 2: Interferenz zweier Kreiswellen in Abhängigkeit von der Wellenlänge und dem Quellenabstand | |||
</gallery> | </gallery> | ||
| Zeile 75: | Zeile 83: | ||
=== Schwebung und stehende Welle === | === Schwebung und stehende Welle === | ||
[[Datei:Interferenz sinus.svg|mini|hochkant=2|''Interferenz zweier [[Sinus]]-Wellen:''<br /> | [[Datei:Interferenz sinus.svg|mini|hochkant=2|Abbildung 3: ''Interferenz zweier [[Sinus]]-Wellen:''<br /> | ||
Es ist der Fall ''vollständig konstruktiver'' und ''vollständig destruktiver'' Interferenz bei Schwingungen gleicher Wellenlänge und gleicher Amplitude gezeigt. Das dritte Beispiel verdeutlicht das Entstehen einer ''[[Schwebung]]''.]] | Es ist der Fall ''vollständig konstruktiver'' und ''vollständig destruktiver'' Interferenz bei Schwingungen gleicher Wellenlänge und gleicher Amplitude gezeigt. Das dritte Beispiel verdeutlicht das Entstehen einer ''[[Schwebung]]''.]] | ||
Überlagert man zwei Wellen mit ungleichen, aber nahe beieinander liegenden Frequenzen <math>\!\ \nu_1</math> und <math>\nu_2\, ,</math> so ergibt sich durch die [[Schwebung]] ein Muster, wie es in | Überlagert man zwei Wellen mit ungleichen, aber nahe beieinander liegenden Frequenzen <math>\!\ \nu_1</math> und <math>\nu_2\, ,</math> so ergibt sich durch die [[Schwebung]] ein Muster, wie es im unteren Graph in Abb. 3 gezeigt ist. Es bildet sich eine schnelle [[Schwingung|Oszillation]] aus (<math>\nu_\text{schnell} = \tfrac{\nu_1 + \nu_2}2\, ,</math> in brauner Farbe), deren Amplitude sich mit einer langsamen Frequenz (<math>\nu_\text{Schwebung} = \tfrac{| \nu_2 - \nu_1 |}2\,</math>, blau) ändert. Betrachtet man Intensitäten mit einem Detektor, so ist zusätzlich noch eine zeitliche Mittelung über das Abtastintervall <math>\tfrac{1}{f_a}</math> durchzuführen, wobei <math>f_a</math> die Abtastfrequenz des Detektors ist. | ||
Für normale Lichtquellen und Frequenzen, die so weit auseinanderliegen, dass Schwebung praktisch keine Rolle spielt, ist das (zeitlich gemittelte) Interferenzmuster die Summe der Interferenzmuster der einzelnen Frequenzen. Das beruht darauf, dass die Interferenz zwischen Wellen mit unterschiedlichen Frequenzen – aufgrund des Fehlens einer festen Phasenbeziehung – in der zeitlichen Mittelung wegfällt.<ref>{{Literatur |Autor=Wolfgang Demtröder |Titel=Experimentalphysik 3. Atome, | Für normale Lichtquellen und Frequenzen, die so weit auseinanderliegen, dass Schwebung praktisch keine Rolle spielt, ist das (zeitlich gemittelte) Interferenzmuster die Summe der Interferenzmuster der einzelnen Frequenzen. Das beruht darauf, dass die Interferenz zwischen Wellen mit unterschiedlichen Frequenzen – aufgrund des Fehlens einer festen Phasenbeziehung – in der zeitlichen Mittelung wegfällt.<ref>{{Literatur |Autor=Wolfgang Demtröder |Titel=Experimentalphysik 3. Atome, Moleküle und Festkörper |Auflage=4. |Verlag=Springer |Datum=2010 |ISBN=978-3-642-03911-9 |Seiten=366 |Online={{Google Buch|BuchID=DFEzhuWhoTsC|Seite=366}}}}</ref> Für dichromatisches Licht erhält man in diesem Fall: | ||
:<math>I=\langle \left| \vec S (t) \right| \rangle _t = \langle c \, \varepsilon _0 \left( \vec E_1 (t) + \vec E_2 (t) \right) ^2 \rangle _t = I_1 + I_2 + \underbrace{\langle 2 c \, \varepsilon _0 \vec E_1 (t) \vec E_2 (t) \rangle _t}_{=0},</math> | :<math>I=\langle \left| \vec S (t) \right| \rangle _t = \langle c \, \varepsilon _0 \left( \vec E_1 (t) + \vec E_2 (t) \right) ^2 \rangle _t = I_1 + I_2 + \underbrace{\langle 2 c \, \varepsilon _0 \vec E_1 (t) \vec E_2 (t) \rangle _t}_{=0},</math> | ||
wobei <math>\vec S</math> der [[Poynting-Vektor]] ist. | wobei <math>\vec S</math> der [[Poynting-Vektor]] ist. | ||
| Zeile 97: | Zeile 105: | ||
<gallery class="centered" perrow="5"> | <gallery class="centered" perrow="5"> | ||
Wismut Kristall und 1cm3 Wuerfel.jpg|Interferenzfarben durch eine Oxidschicht auf dem Metall [[Bismut]] | Datei:Wismut Kristall und 1cm3 Wuerfel.jpg|Interferenzfarben durch eine Oxidschicht auf dem Metall [[Bismut]] | ||
Spectral color in broken ice 02.JPG|Interferenzfarben in gebrochenem Eis | Datei:Spectral color in broken ice 02.JPG|Interferenzfarben in gebrochenem Eis | ||
Interferencia lakkretegen2.jpg|Interferenzfarben in Nagellackschicht | Datei:Interferencia lakkretegen2.jpg|Interferenzfarben in Nagellackschicht | ||
Purpurkehlnymphe.jpg|Interferenzfarben im Gefieder der Purpurkehlnymphe | Datei:Purpurkehlnymphe.jpg|Interferenzfarben im Gefieder der Purpurkehlnymphe | ||
Opal-black1.jpg|Schwarzer Edelopal mit vollem, opalisierendem Farbenspiel | Datei:Opal-black1.jpg|Schwarzer Edelopal mit vollem, opalisierendem Farbenspiel | ||
</gallery> | </gallery> | ||
| Zeile 145: | Zeile 153: | ||
Der Arbeitsgruppe von [[Anton Zeilinger]] ist es 1999 gelungen, ein Interferenzmuster von [[Fullerene]]n (Molekülen aus 60 oder 70 [[Kohlenstoff]]-Atomen) zu beobachten. Dieses sind bei weitem nicht die schwersten Teilchen, für die Quanteninterferenz beobachtet werden konnte.<ref name="Arndt1999">{{Literatur |Autor=Markus Arndt, Olaf Nairz, Julian Vos-Andreae, Claudia Keller, Gerbrand van der Zouw, Anton Zeilinger |Titel=Wave–particle duality of C<sub>60</sub> molecules |Sammelwerk=Nature |Band=401 |Nummer=6754 |Datum=1999-10-14 |Seiten=680–682 |Online=[http://www.atomwave.org/rmparticle/ao%20refs/aifm%20pdfs%20by%20group%20leaders/arndt%20pdfs/ANV99%20C60%20duality.pdf PDF] |DOI=10.1038/44348 |Abruf=2014-05-18}}</ref><ref>{{Literatur |Autor=Björn Brezger, Lucia Hackermüller, Stefan Uttenthaler, Julia Petschinka, Markus Arndt, Anton Zeilinger |Titel=Matter-Wave Interferometer for Large Molecules |Sammelwerk=Physical Review Letters |Band=88 |Nummer=10 |Datum=2002-02-26 |Seiten=100404 |DOI=10.1103/PhysRevLett.88.100404}}</ref> | Der Arbeitsgruppe von [[Anton Zeilinger]] ist es 1999 gelungen, ein Interferenzmuster von [[Fullerene]]n (Molekülen aus 60 oder 70 [[Kohlenstoff]]-Atomen) zu beobachten. Dieses sind bei weitem nicht die schwersten Teilchen, für die Quanteninterferenz beobachtet werden konnte.<ref name="Arndt1999">{{Literatur |Autor=Markus Arndt, Olaf Nairz, Julian Vos-Andreae, Claudia Keller, Gerbrand van der Zouw, Anton Zeilinger |Titel=Wave–particle duality of C<sub>60</sub> molecules |Sammelwerk=Nature |Band=401 |Nummer=6754 |Datum=1999-10-14 |Seiten=680–682 |Online=[http://www.atomwave.org/rmparticle/ao%20refs/aifm%20pdfs%20by%20group%20leaders/arndt%20pdfs/ANV99%20C60%20duality.pdf PDF] |DOI=10.1038/44348 |Abruf=2014-05-18}}</ref><ref>{{Literatur |Autor=Björn Brezger, Lucia Hackermüller, Stefan Uttenthaler, Julia Petschinka, Markus Arndt, Anton Zeilinger |Titel=Matter-Wave Interferometer for Large Molecules |Sammelwerk=Physical Review Letters |Band=88 |Nummer=10 |Datum=2002-02-26 |Seiten=100404 |DOI=10.1103/PhysRevLett.88.100404}}</ref> | ||
Die Forschungsgruppe rund um [[Markus Arndt]] setzte die von Zeilinger initiierten Experimente an der [[Universität Wien]] fort und konnte 2010 Quanteninterferenz mit Molekülen aus bis zu 430 Atomen und Massen bis fast 7000 [[Atomare Masseneinheit|atomaren Masseneinheiten]] zeigen.<ref name="Gerlich2010">Stefan Gerlich, Sandra Eibenberger, Mathias Tomandl, Stefan Nimmrichter, Klaus Hornberger, Paul J. Fagan, Jens Tüxen, Marcel Mayor, Markus Arndt: ''Quantum interference of large organic molecules.'' In: ''Nature Communications'' 2, Article 263, [[doi:10.1038/ncomms1263]]</ref> | Die Forschungsgruppe rund um [[Markus Arndt]] setzte die von Zeilinger initiierten Experimente an der [[Universität Wien]] fort und konnte 2010 Quanteninterferenz mit Molekülen aus bis zu 430 Atomen und Massen bis fast 7000 [[Atomare Masseneinheit|atomaren Masseneinheiten]] zeigen.<ref name="Gerlich2010">Stefan Gerlich, Sandra Eibenberger, Mathias Tomandl, Stefan Nimmrichter, [[Klaus Hornberger]], Paul J. Fagan, Jens Tüxen, Marcel Mayor, Markus Arndt: ''Quantum interference of large organic molecules.'' In: ''Nature Communications'' 2, Article 263, [[doi:10.1038/ncomms1263]]</ref> | ||
Bemerkenswert an dieser Form von Interferenz ist allerdings, dass die Messung, welchen Weg ein Quantenobjekt gewählt hat („Welcher-Weg“-Information), dazu führt, dass auch nur noch dieser „benutzt“ wird – also keine Interferenz auftritt. In einer Doppelspaltanordnung hängt das Interferenzmuster also davon ab, ob man herausfinden kann, welchen Weg (durch Spalt 1 oder Spalt 2) das Quantenobjekt nahm. Dies gilt auch, wenn der Weg des Quantenobjekts nicht schon beim Passieren der Spalte, sondern erst später festgestellt wird (verzögerter Messprozess). Nur wenn eine Gewinnung der „Welcher-Weg“-Information nie erfolgte oder sie durch einen [[Quantenradierer]] wieder getilgt wurde, ergibt sich hinter dem Doppelspalt ein Interferenzbild.<ref>{{Literatur |Autor=Michael Springer |Titel=Welle oder Teilchen – ein Test mit dem Quantenradierer |Sammelwerk=[[Spektrum der Wissenschaft]] |Band=1 |Verlag=Spektrum der Wissenschaft Akademischer Verlag |Datum=1996 |Seiten=}}</ref> | Bemerkenswert an dieser Form von Interferenz ist allerdings, dass die Messung, welchen Weg ein Quantenobjekt gewählt hat („Welcher-Weg“-Information), dazu führt, dass auch nur noch dieser „benutzt“ wird – also keine Interferenz auftritt. In einer Doppelspaltanordnung hängt das Interferenzmuster also davon ab, ob man herausfinden kann, welchen Weg (durch Spalt 1 oder Spalt 2) das Quantenobjekt nahm. Dies gilt auch, wenn der Weg des Quantenobjekts nicht schon beim Passieren der Spalte, sondern erst später festgestellt wird (verzögerter Messprozess). Nur wenn eine Gewinnung der „Welcher-Weg“-Information nie erfolgte oder sie durch einen [[Quantenradierer]] wieder getilgt wurde, ergibt sich hinter dem Doppelspalt ein Interferenzbild.<ref>{{Literatur |Autor=Michael Springer |Titel=Welle oder Teilchen – ein Test mit dem Quantenradierer |Sammelwerk=[[Spektrum der Wissenschaft]] |Band=1 |Verlag=Spektrum der Wissenschaft Akademischer Verlag |Datum=1996 |Seiten=}}</ref> | ||
| Zeile 155: | Zeile 163: | ||
</math> | </math> | ||
Für die Wahrscheinlichkeit, dass ein System im Zustand <math>|\psi\rangle</math> | Für die Wahrscheinlichkeit, dass ein System im Zustand <math>|\psi\rangle</math> bei der Messung den Zustand <math>|\phi\rangle</math> ergibt lautet dann: | ||
:<math> | :<math> | ||
\mathcal{P}(\psi\rightarrow\phi)=|\langle\psi|\phi\rangle|^2=\left|\sum\limits_{i}c_i^\ast b_i\right|^2 =\sum\limits_{i,j}c_i^\ast c_jb_i^\ast b_j=\sum\limits_i|c_i|^2|b_i|^2+\sum\limits_{i\neq j}c_i^\ast c_jb_i^\ast b_j\, | \mathcal{P}(\psi\rightarrow\phi)=|\langle\psi|\phi\rangle|^2=\left|\sum\limits_{i}c_i^\ast b_i\right|^2 =\sum\limits_{i,j}c_i^\ast c_jb_i^\ast b_j=\sum\limits_i|c_i|^2|b_i|^2+\sum\limits_{i\neq j}c_i^\ast c_jb_i^\ast b_j\, | ||
| Zeile 177: | Zeile 185: | ||
* [http://www.gfai.de/~heinz/historic/pressinf/bilder_d.htm Simulationen mit Zeitfunktionen] | * [http://www.gfai.de/~heinz/historic/pressinf/bilder_d.htm Simulationen mit Zeitfunktionen] | ||
* [http://www.raacke.de/airy.html Online-Rechner für Interferenzfarben an dünnen Schichten] | * [http://www.raacke.de/airy.html Online-Rechner für Interferenzfarben an dünnen Schichten] | ||
* [http://www.fairaudio.de/hifi-lexikon-begriffe/interferenz.html Bedeutung der Interferenz in der Audiotechnik (incl. Grafiken)] | * [http://www.fairaudio.de/hifi-lexikon-begriffe/interferenz.html Bedeutung der Interferenz in der Audiotechnik (incl. Grafiken)] | ||
* [http://www.quantumlab.de/ Interferenz von einzelnen Photonen im Interferometer mit Quantenradierer] (QuantumLab) | * [http://www.quantumlab.de/ Interferenz von einzelnen Photonen im Interferometer mit Quantenradierer] (QuantumLab) | ||
* [ | * [https://www.leifiphysik.de/optik/beugung-und-interferenz Beugung und Interferenz] ([[LEIFI]]) | ||
* [http://gerdbreitenbach.de/lissajous/lissajous.html Simulation zu Interferenz zweier stehender Wellen] | * [http://gerdbreitenbach.de/lissajous/lissajous.html Simulation zu Interferenz zweier stehender Wellen] | ||
* [https://www.youtube.com/watch?v=qZgKjZC1uqY Animierter Film zur Farbe von Seifenblasen (englisch)] | * [https://www.youtube.com/watch?v=qZgKjZC1uqY Animierter Film zur Farbe von Seifenblasen (englisch)] | ||
| Zeile 192: | Zeile 199: | ||
[[Kategorie:Akustik]] | [[Kategorie:Akustik]] | ||
[[Kategorie:Wellenlehre]] | [[Kategorie:Wellenlehre]] | ||
Aktuelle Version vom 16. Januar 2022, 00:59 Uhr
Interferenz (lat. {{Modul:Vorlage:lang}} Modul:Multilingual:149: attempt to index field 'data' (a nil value) ‚zwischen‘ und {{Modul:Vorlage:lang}} Modul:Multilingual:149: attempt to index field 'data' (a nil value) über altfrz. {{Modul:Vorlage:lang}} Modul:Multilingual:149: attempt to index field 'data' (a nil value) ‚sich gegenseitig schlagen‘)[1] beschreibt die Änderung der Amplitude bei der Überlagerung von zwei oder mehr Wellen nach dem Superpositionsprinzip – also die vorzeichenrichtige Addition ihrer Auslenkungen (nicht der Intensitäten) während ihrer Durchdringung. Interferenz tritt bei allen Arten von Wellen auf, also bei Schall-, Licht-, Materiewellen usw.
An Orten, wo sich die Wellen dabei gegenseitig auslöschen, herrscht destruktive Interferenz. An Orten, wo sie sich verstärken, herrscht konstruktive Interferenz. Ein Zeichen für das Auftreten von Interferenz zweier Wellenfelder sind abwechselnde Maxima und Minima der Intensität, wo jedes Wellenfeld für sich eine gleichmäßige Intensität hatte. Diese Folge von konstruktiver und destruktiver Interferenz wird als Interferenzmuster bezeichnet. Ein bekanntes Beispiel sind die hellen bzw. dunklen Streifen beim Doppelspaltversuch. Das Auftreten von Interferenz im physikalischen Experiment gilt als Nachweis für die Wellennatur der untersuchten Strahlung.
Grundlagen und Voraussetzungen
Kohärenz

Das Wellenfeld, das aus der Interferenz zweier (oder mehrerer) Wellen entsteht, kann nur dann zeitlich stabil sein, wenn diese Wellen untereinander eine (zeitlich) feste Phasenbeziehung aufweisen. Man spricht dann von kohärenten Wellen. Sind die Wellen nicht monochromatisch, bestehen also aus einer ganzen Reihe von Frequenzanteilen, so definiert man eine Kohärenzzeit, die beschreibt, wie die Wellen maximal gegeneinander verschoben sein dürfen, um noch ein stabiles Wellenfeld zu erzeugen. Diese Kohärenzzeit (oder die daraus abgeleitete Kohärenzlänge) ist ein wichtiges Maß für physikalische Lichtquellen.
Destruktive Interferenz
Zwei Wellen löschen sich gegenseitig völlig aus, wenn ihre Auslenkungen am betrachteten Ort und Zeitpunkt entgegengesetzt gleich sind. Damit das an diesem Ort für längere Zeit so bleibt, müssen harmonische (d. h. sinusförmige) Wellen gleiche Frequenz haben und um eine halbe Schwingungsperiode bzw. eine halbe Wellenlänge gegeneinander versetzt sein (siehe Phasenverschiebung bzw. Gangunterschied). Bei transversalen Wellen (z. B. Licht) müssen die Auslenkungen in derselben Ebene liegen, bei komplexen Wellen (z. B. quantenmechanische Wellenfunktion) muss die komplexe Phase der Amplitude übereinstimmen.
Polarisation
Schallwellen in Festkörpern und elektromagnetische Wellen können polarisiert sein. Untersuchungen zur Interferenz von polarisiertem Licht führten 1817 zu der Erkenntnis, dass es sich bei Lichtwellen um Transversalwellen handelt, siehe Fresnel-Arago-Gesetze. Danach interferieren Wellen, wenn sie senkrecht zueinander polarisiert sind, nicht. Das gilt aber nur für die Beobachtung mit Detektoren, die wie die oben angeführten Beispiele lediglich die Intensität (proportional zum Betragsquadrat der Wellenamplitude des elektrischen Anteils der Welle) messen.[2]
Mathematische Darstellung
Eine Welle wird üblicherweise durch eine Funktion von Ort $ \!\ x $ und Zeit $ \!\ t $ geschrieben $ f(\mathbf {x} ,t)\,. $ Dieses bringt zum Ausdruck, dass sich eine Welle sowohl im Raum, als auch in der Zeit ausbreitet. Überlagern sich nun mehrere Wellen $ f_{i}(\mathbf {x} ,t) $ an einem Ort $ \mathbf {x_{0}} \,, $ so lässt sich das Wellenfeld dort als Superposition (Summe) der einzelnen Wellen darstellen:
- $ f_{\mathrm {ges} }(\mathbf {x_{0}} ,t)=\sum \limits _{i}f_{i}(\mathbf {x_{0}} ,t)\, $.
Interferenz zweier Wellen gleicher Frequenz und Amplitude, aber unterschiedlicher Phase
Die Überlagerung zweier Wellen gleicher Frequenz und Amplitude lässt sich anhand der trigonometrischen Additionstheoreme berechnen. Werden die beiden Wellen $ f_{1}(t) $ und $ f_{2}(t) $ mit der gemeinsamen Frequenz $ \omega $, der Amplitude $ a $ und den Phasen $ \varphi _{1} $ und $ \varphi _{2} $ durch
- $ f_{1}(t)=a\cdot \sin(\omega \cdot t+\varphi _{1}) $ und $ f_{2}(t)=a\cdot \sin(\omega \cdot t+\varphi _{2})\, $
beschrieben, so ergibt sich für die resultierende Überlagerung der Wellen
- $ f_{1}(t)+f_{2}(t)=a\left(\sin(\omega t+\varphi _{1})+\sin(\omega t+\varphi _{2})\right)=2a\cos \left({\frac {\varphi _{1}-\varphi _{2}}{2}}\right)\sin \left(\omega t+{\frac {\varphi _{1}+\varphi _{2}}{2}}\right)\, $,
d. h., es entsteht eine Welle derselben Frequenz, deren Amplitude von der Differenz der Phasen der beiden ursprünglichen Wellen abhängt und deren Phase das Mittel der Phasen der ursprünglichen Wellen ist.
Für gleiche Phasen der Wellen ($ \varphi _{1}=\varphi _{2} $) wird der Cosinus Eins. Es ergibt sich eine Amplitude von $ 2a $, d. h., die Amplitude verdoppelt sich gegenüber den Ausgangsamplituden, was konstruktiver Interferenz entspricht.
Für eine Phasendifferenz von 180° ($ \varphi _{1}=\varphi _{2}+\pi $) wird der Cosinus Null, d. h., die resultierende Welle verschwindet. Dieses entspricht destruktiver Interferenz.
Interferenz zweier Wellen gleicher Frequenz aber unterschiedlicher Amplitude und Phase
Für gleiche Frequenz der Wellen, aber unterschiedliche Amplituden und Phasen lässt sich die resultierende Welle mittels Zeigerarithmetik berechnen. Die beiden Wellen $ g_{1}(t) $ und $ g_{2}(t) $ besitzen die gemeinsame Frequenz $ \omega $, die Amplituden $ a_{1} $ und $ a_{2} $ und die Phasen $ \varphi _{1} $ und $ \varphi _{2} $
- $ g_{1}(t)=a_{1}\cdot \sin(\omega t+\varphi _{1}) $ und $ g_{2}(t)=a_{2}\cdot \sin(\omega t+\varphi _{2})\, $.
Die resultierende Überlagerung der Wellen hat die Form:
- $ g_{1}(t)+g_{2}(t)=A\cdot \sin(\omega t+\varphi )\, $
mit der Amplitude:
- $ A={\sqrt {a_{1}^{2}+a_{2}^{2}+2a_{1}a_{2}\cos(\varphi _{1}-\varphi _{2})}}\, $
und der Phase $ \varphi $
- $ \tan \varphi ={\frac {a_{1}\sin(\varphi _{1})+a_{2}\sin(\varphi _{2})}{a_{1}\cos(\varphi _{1})+a_{2}\cos(\varphi _{2})}}\, $.
Überlagerung von Kreiswellen
Die Abbildung 1 zeigt die Interferenz von zwei kreisförmigen Wellengruppen gleicher Wellenlänge und Amplitude. Die Kreuze markieren die Lage der Quellen, die Kreise die Maxima der jeweiligen Teilwelle. An weißen Stellen tritt konstruktive Interferenz, in positiver Richtung, an schwarzen konstruktive Interferenz, in negativer Richtung, auf. An den grauen Stellen herrscht destruktive Interferenz. Es ist zu erkennen, dass die Minima auf einer Hyperbelschar liegen, deren Brennpunkte identisch den Quellorten der Wellen sind. Man spricht deshalb bei zwei Punktquellen von einer hyperbolischen Interferenz. Die Hyperbel ist dabei die Kurve aller Punkte, die zu den zwei Quellorten die Laufzeitdifferenz $ t={\tfrac {\lambda }{2}} $ haben. Der Scheitelpunktabstand $ \!\ 2a $ entspricht der Laufzeitdifferenz $ \!\ 2a=(T_{1}-T_{2})v $, wenn $ \!\ T_{1} $ und $ \!\ T_{2} $ den Zeitbezug der beiden speisenden Zeitfunktionen darstellen und $ v $ die mediale Ausbreitungsgeschwindigkeit darstellt.
In der Abbildung 2 wird die Veränderung des Interferenzbildes in Abhängigkeit von der Wellenlänge (nimmt von oben nach unten zu) und in Abhängigkeit vom Abstand der Quellen (nimmt von links nach rechts zu) demonstriert. In den dunklen Bereichen (um die Interferenzminima) liegt destruktive und in den hellen (Maxima) konstruktive Interferenz vor.
Bekannte physikalische Erscheinungen
Es gibt zahlreiche physikalische Erscheinungen, die auf der Interferenz von Wellen, meist elektromagnetischer Wellen (Licht), basieren. Im Folgenden sollen einige bekannte Beispiele aus verschiedenen Bereichen kurz beschrieben werden.
Schwebung und stehende Welle
Es ist der Fall vollständig konstruktiver und vollständig destruktiver Interferenz bei Schwingungen gleicher Wellenlänge und gleicher Amplitude gezeigt. Das dritte Beispiel verdeutlicht das Entstehen einer Schwebung.
Überlagert man zwei Wellen mit ungleichen, aber nahe beieinander liegenden Frequenzen $ \!\ \nu _{1} $ und $ \nu _{2}\,, $ so ergibt sich durch die Schwebung ein Muster, wie es im unteren Graph in Abb. 3 gezeigt ist. Es bildet sich eine schnelle Oszillation aus ($ \nu _{\text{schnell}}={\tfrac {\nu _{1}+\nu _{2}}{2}}\,, $ in brauner Farbe), deren Amplitude sich mit einer langsamen Frequenz ($ \nu _{\text{Schwebung}}={\tfrac {|\nu _{2}-\nu _{1}|}{2}}\, $, blau) ändert. Betrachtet man Intensitäten mit einem Detektor, so ist zusätzlich noch eine zeitliche Mittelung über das Abtastintervall $ {\tfrac {1}{f_{a}}} $ durchzuführen, wobei $ f_{a} $ die Abtastfrequenz des Detektors ist.
Für normale Lichtquellen und Frequenzen, die so weit auseinanderliegen, dass Schwebung praktisch keine Rolle spielt, ist das (zeitlich gemittelte) Interferenzmuster die Summe der Interferenzmuster der einzelnen Frequenzen. Das beruht darauf, dass die Interferenz zwischen Wellen mit unterschiedlichen Frequenzen – aufgrund des Fehlens einer festen Phasenbeziehung – in der zeitlichen Mittelung wegfällt.[3] Für dichromatisches Licht erhält man in diesem Fall:
- $ I=\langle \left|{\vec {S}}(t)\right|\rangle _{t}=\langle c\,\varepsilon _{0}\left({\vec {E}}_{1}(t)+{\vec {E}}_{2}(t)\right)^{2}\rangle _{t}=I_{1}+I_{2}+\underbrace {\langle 2c\,\varepsilon _{0}{\vec {E}}_{1}(t){\vec {E}}_{2}(t)\rangle _{t}} _{=0}, $
wobei $ {\vec {S}} $ der Poynting-Vektor ist.
Zum Stimmen von Musikinstrumenten kann man die entsprechende Einstellung solange verändern, bis man zusammen mit einem Referenzton (bspw. aus einer Stimmgabel) keine Schwebung mehr wahrnimmt. Die Vermessung von Schwebungssignalen kann auch zur Messung von ansonsten (für das Messgerät) zu hohen Frequenzen genutzt werden. Dazu ist allerdings eine Signalquelle notwendig, die Signale mit sehr stabiler und präziser Frequenz liefert.
Die Interferenz zweier Wellen gleicher Wellenlänge, aber mit entgegengesetzter Ausbreitungsrichtung führt zu einer stehenden Welle.
Doppelspaltexperiment
Mit dem Doppelspaltexperiment erbrachte Thomas Young 1802 erstmals Belege für die Wellennatur des Lichts. Bei diesem Versuch wird in dem Weg eines Lichtstrahls eine Blende mit einem Doppelspalt aufgestellt, wobei der Abstand der Spalte in der Größenordnung der Wellenlänge liegt. Dahinter befindet sich ein Schirm, auf dem sich bei genügend großem Abstand der Lichtquelle vom Schirm ein Interferenzmuster bildet. Ist nur ein Spalt offen und breit genug, so bildet sich das typische Beugungsmuster eines Einfachspalts. Analog lässt sich mit einem Elektronenstrahl der Wellencharakter von Elektronen zeigen, darauf wird im Abschnitt über Interferenz in der Quantenmechanik (s. u.) näher eingegangen.
Interferenzfarben
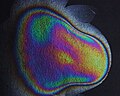
Weißes Licht, welches an dünnen Schichten optisch transparenter Materialien (wie z. B. einem Ölfilm auf Wasser, einer dünnen Oxidschicht auf Metallen, oder einfach Seifenblasen) reflektiert wird, erscheint häufig farbig. Dabei interferiert das Licht, das an der oberen und unteren Grenzfläche der dünnen Schicht reflektiert wird. Richtungsabhängig wird dann das Licht einer bestimmten Wellenlänge ausgelöscht und es bleibt nur die Komplementärfarbe zum ausgelöschten Licht übrig.[4]
Ein bekanntes Beispiel für das Auftreten von Interferenzfarben an zwei eng benachbarten Oberflächen sind die Newton-Ringe.[5] Hierbei liegt eine Sammellinse mit langer Brennweite auf einer ebenen Glasplatte auf. Um den Berührungspunkt herum entsteht zwischen den Glasoberflächen ein Spalt mit langsam nach außen hin zunehmender Dicke. Wird diese Anordnung mit monochromatischem Licht von oben beleuchtet, treten sowohl in Reflexion als auch in Durchsicht konzentrische helle und dunkle Ringe rund um den Berührungspunkt von Linse und Glasplatte auf. Wird die Versuchsanordnung mit weißem Licht ausgeleuchtet, dann entstehen farbige, konzentrische Ringe. Die Breite der Ringe und die Intensität ihrer Farben nimmt mit zunehmendem Radius ab.
Die irisierenden Farben der Opaleszenz sind ebenfalls eine Folge von Interferenz. Dabei wird das Licht an kleinen Strukturen im Inneren des Materials gestreut. Die Farben vieler Schmetterlinge, einiger besonders prächtig schillernder Vögel oder des Edelsteins Opal beruhen auf diesem Effekt. Sie werden daher auch Strukturfarben genannt.
Weißlichtinterferenz
Die Überlagerung kontinuierlich variierender Wellenlänge und Amplitude (Spektrum) erzeugt ein Interferenzmuster nur innerhalb der Kohärenzlänge. In der Weißlichtinterferometrie wird dieses Verhalten ausgenutzt, um eine eindeutige Längenmessung zu erhalten. Ein weiteres Anwendungsbeispiel findet sich in der Optischen Kohärenztomografie, die dadurch dreidimensionale Strukturen erfassen kann.
Laser-Speckle
Das Licht eines aufgeweiteten Laserstrahls weist eine nahezu perfekte Kohärenz senkrecht zum Strahl auf. Dieses führt dazu, dass Laserlicht auch nach der Reflexion an unebenen Oberflächen noch interferenzfähig ist. Dann dient jeder Punkt der Fläche als Streuzentrum/Punktquelle einer sekundären Kugelwelle. Eine optische Abbildung dieser Punktquellen überlagert im Bild das Licht, das einen Bildpunkt auf unterschiedlichen Wegen erreicht. Diese Überlagerung führt am Bildpunkt zu Interferenz. Deren Ergebnis ist abhängig von der genauen Lauflänge des Lichtes zwischen Punktquelle und Bildpunkt. Ein Weglängenunterschied in der Größe der halben Wellenlänge des Lichtes entscheidet über destruktive oder konstruktive Interferenz. Insgesamt ergibt sich ein zufällig verteiltes Punktmuster am Ort der Abbildung.
Anwendungen in der Technik
Antischall
In der Akustik wird destruktive Interferenz zur Reduktion von störenden Geräuschen ausgenutzt, sogenannter Antischall. Dieses Prinzip kommt z. B. in Kopfhörern für Flugzeugpiloten zum Einsatz, um den Maschinenlärm lokal zu dämpfen.[6]
Interferometer
In der Messtechnik werden Interferometer eingesetzt. Diese nutzen Interferenzerscheinungen zur Messung von Längen oder Phasenverschiebungen mit sehr hoher Auflösung. Dazu wird ein (Licht-)Strahl in zwei kohärente Teile aufgespaltet, die später wieder überlagert werden. Die beiden Strahlen legen dabei unterschiedliche Strecken $ \!\ s_{1} $ und $ \!\ s_{2} $ zurück. Unterscheiden diese sich um ein ganzzahliges Vielfaches der Wellenlänge, so erhält man am Ausgang des Interferometers konstruktive Interferenz. Unterscheiden sie sich um eine halbe Wellenlänge (Phasenverschiebung $ \Delta \varphi =180^{\circ } $), so erhält man destruktive Interferenz. Stellt man nun das Interferometer zunächst auf konstruktive Interferenz ein und führt dann eine zusätzliche Phasenverschiebung $ \!\ \Delta \varphi $ in einem der beiden Arme ein, so kann man diese über die Intensität am Ausgang des Interferometers bestimmen.
Es gibt verschiedene Umsetzungen dieses Prinzips: Mach-Zehnder-Interferometer, Michelson-Interferometer, Sagnac-Interferometer, Fabry-Pérot-Interferometer etc.
Funktechnik
Durch Phasenverschiebung zwischen den Antennenelementen einer Phased-Array-Antenne kann die Beobachtungsrichtung sehr schnell umgeschaltet werden. Die genaue Analyse der Phasenverschiebungen zwischen den Einzelantennen von Radioteleskopen erlaubt es, die Richtung entfernter Strahlungsquellen außerordentlich exakt zu ermitteln. Ein Antennendiagramm zeigt die Strahlungscharakteristik von Einzelantennen oder Antennengruppen, deren Gestalt durch Interferenz festgelegt wird. Bei der Yagi-Uda-Antenne wird auf diese Weise die Strahlungsenergie in eine schmale Vorwärtskeule gebündelt, wodurch sich die gewünschte Richtwirkung ergibt.
Im Balanced Duplexer wird bei hoher Sendeleistung eine Gasentladungsröhre gezündet, die auf die Wellen fast wie ein Kurzschluss wirkt. Durch geschickte Energieverteilung auf zwei getrennte Zweige eines Hohlleiters mit unterschiedlicher Phasenverschiebung und anschließendes Zusammenführen beider Anteile wird erreicht, dass die Sendeenergie zur Antenne fließt (konstruktive Interferenz) und nicht zum Empfänger (destruktive Interferenz).
Ein Diplexer ermöglicht durch destruktive bzw. konstruktive Interferenz in getrennten Zweigen einer Anordnung aus Hohlleitern, dass zwei Funkgeräte unterschiedlicher Wellenlänge mit einer Antenne betrieben werden können. Auf ähnliche Weise wird in einem Ringkoppler die Summe bzw. Differenz zweier gleichfrequenter Signale gebildet.
Interferenz in der Quantenmechanik
Anschauliche Erklärung
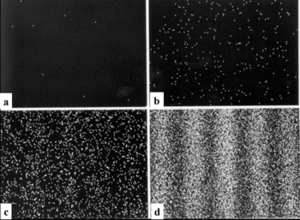
In der Quantenmechanik spielen Interferenzphänomene eine entscheidende Rolle. Teilchen (und allgemeiner beliebige Zustände eines Systems) werden durch Wellenfunktionen beschrieben. Diese sind die Lösungen der Schrödingergleichung, die eine Form ähnlich einer Wellengleichung annehmen kann. Damit können sich Teilchen, also Materie, in der Quantenmechanik wie Wellen verhalten und auch interferieren (siehe auch Welle-Teilchen-Dualismus, Materiewellen). Ein bekanntes Beispiel ist etwa die Interferenz von Elektronen in einem Doppelspaltexperiment[7] (siehe die Bilder rechts) oder die Interferenz zweier Bose-Einstein-Kondensate.
Der Arbeitsgruppe von Anton Zeilinger ist es 1999 gelungen, ein Interferenzmuster von Fullerenen (Molekülen aus 60 oder 70 Kohlenstoff-Atomen) zu beobachten. Dieses sind bei weitem nicht die schwersten Teilchen, für die Quanteninterferenz beobachtet werden konnte.[8][9] Die Forschungsgruppe rund um Markus Arndt setzte die von Zeilinger initiierten Experimente an der Universität Wien fort und konnte 2010 Quanteninterferenz mit Molekülen aus bis zu 430 Atomen und Massen bis fast 7000 atomaren Masseneinheiten zeigen.[10]
Bemerkenswert an dieser Form von Interferenz ist allerdings, dass die Messung, welchen Weg ein Quantenobjekt gewählt hat („Welcher-Weg“-Information), dazu führt, dass auch nur noch dieser „benutzt“ wird – also keine Interferenz auftritt. In einer Doppelspaltanordnung hängt das Interferenzmuster also davon ab, ob man herausfinden kann, welchen Weg (durch Spalt 1 oder Spalt 2) das Quantenobjekt nahm. Dies gilt auch, wenn der Weg des Quantenobjekts nicht schon beim Passieren der Spalte, sondern erst später festgestellt wird (verzögerter Messprozess). Nur wenn eine Gewinnung der „Welcher-Weg“-Information nie erfolgte oder sie durch einen Quantenradierer wieder getilgt wurde, ergibt sich hinter dem Doppelspalt ein Interferenzbild.[11]
Mathematische Fassung
In der Bra-Ket-Notation lässt sich ein beliebiger quantenmechanischer Zustand in einer orthonormierten Basis $ \{|i\rangle \} $ ($ \langle i|j\rangle =\delta _{ij} $) darstellen. Dabei sind die $ c_{i},b_{i}\in \mathbb {C} $ komplexe Koeffizienten:
- $ |\psi \rangle =\sum \limits _{i}c_{i}\cdot |i\rangle ,\ \ \ \ \ \ \ \ \ \ |\phi \rangle =\sum \limits _{i}b_{i}\cdot |i\rangle \, $
Für die Wahrscheinlichkeit, dass ein System im Zustand $ |\psi \rangle $ bei der Messung den Zustand $ |\phi \rangle $ ergibt lautet dann:
- $ {\mathcal {P}}(\psi \rightarrow \phi )=|\langle \psi |\phi \rangle |^{2}=\left|\sum \limits _{i}c_{i}^{\ast }b_{i}\right|^{2}=\sum \limits _{i,j}c_{i}^{\ast }c_{j}b_{i}^{\ast }b_{j}=\sum \limits _{i}|c_{i}|^{2}|b_{i}|^{2}+\sum \limits _{i\neq j}c_{i}^{\ast }c_{j}b_{i}^{\ast }b_{j}\, $
Wichtig ist hier, dass nicht die Aufenthaltswahrscheinlichkeiten der Teilchen $ \rho (x)=|\langle x|\psi \rangle |^{2} $ überlagert werden, sondern die (komplexen) Wellenfunktionen selbst. Würden die Aufenthaltswahrscheinlichkeiten überlagert, so würde man in obiger Formel den hinteren Interferenzanteil verlieren und das Interferenzmuster verschwindet.
De Broglie postulierte bereits Anfang des 20. Jahrhunderts, dass allen massiven Teilchen eine Wellenlänge $ \lambda ={\tfrac {h}{p}} $ zugeschrieben werden kann, wobei $ \!\ p $ der Impuls des Teilchens ist und $ \!\ h $ das Plancksche Wirkungsquantum. Mit dieser Wellenlänge kann man direkt die Wellenfunktion $ f({\vec {x}},t) $ für ein Teilchen konstruieren und so die Interferenzmuster mit den weiter oben für Licht beschriebenen Methoden berechnen.
Siehe auch
Literatur
- Claude Cohen-Tannoudji, Bernard Diu, Franck Laloë, Joachim Streubel, Jochen Balla: Quantenmechanik. Band 1. 3. Auflage. Walter de Gruyter, Berlin/New York 2007, ISBN 3-11-019324-8.
- Claude Cohen-Tannoudji, Bernard Diu, Franck Laloe: Quantenmechanik. Band 2. 3. Auflage. Walter de Gruyter, Berlin/New York 2008, ISBN 3-11-020149-6.
Weblinks
- Interaktive Animationen zur Interferenz und Überlagerung von Wellen
- Graphische Lösung von Überlagerungen
- Simulationen mit Zeitfunktionen
- Online-Rechner für Interferenzfarben an dünnen Schichten
- Bedeutung der Interferenz in der Audiotechnik (incl. Grafiken)
- Interferenz von einzelnen Photonen im Interferometer mit Quantenradierer (QuantumLab)
- Beugung und Interferenz (LEIFI)
- Simulation zu Interferenz zweier stehender Wellen
- Animierter Film zur Farbe von Seifenblasen (englisch)
- Video: Erzeugung und Überlagerung kohärenter Wellen zu Interferenzstrukturen. Institut für den Wissenschaftlichen Film (IWF) 2004, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.3203/IWF/C-14880.
Einzelnachweise
- ↑ R. E. Allen, H. W. Fowler, F. G. Fowler: The Concise Oxford dictionary of current English. Clarendon Press/Oxford University Press, Oxford/New York 1990, ISBN 0-19-861200-1.
- ↑ B. M. Rodríguez-Lara und I. Ricardez-Vargas: Interference with polarized light beams: Generation of spatially varying polarization. In: American Journal of Physics. 77, 2009, S. 1135–1143, arxiv:0904.0204.
- ↑ Wolfgang Demtröder: Experimentalphysik 3. Atome, Moleküle und Festkörper. 4. Auflage. Springer, 2010, ISBN 978-3-642-03911-9, S. 366 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Helmut Lindner, Wolfgang Siebke (Bearb.): Physik für Ingenieure. Fachbuchverl. Leipzig im Carl-Hanser-Verl., München/Wien 2006, ISBN 978-3-446-40609-4, S. 389.
- ↑ Hans Joachim Eichler, Heinz-Detlef Kronfeldt, Jürgen Sahm: Das Neue Physikalische Grundpraktikum. Springer, 2006, ISBN 978-3-540-21453-3, S. 409 ff. (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Katja Bammel: Schall gegen Schall – aktive Larmunterdruckung. In: Physik Journal. Band 6, Nr. 2, 2007, S. 42 (PDF [abgerufen am 18. Mai 2014]).
- ↑ A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, H. Ezawa: Demonstration of single‐electron buildup of an interference pattern. In: American Journal of Physics. Band 57, Nr. 2, 1. Februar 1989, S. 117–120, doi:10.1119/1.16104.
- ↑ Markus Arndt, Olaf Nairz, Julian Vos-Andreae, Claudia Keller, Gerbrand van der Zouw, Anton Zeilinger: Wave–particle duality of C60 molecules. In: Nature. Band 401, Nr. 6754, 14. Oktober 1999, S. 680–682, doi:10.1038/44348 (PDF [abgerufen am 18. Mai 2014]).
- ↑ Björn Brezger, Lucia Hackermüller, Stefan Uttenthaler, Julia Petschinka, Markus Arndt, Anton Zeilinger: Matter-Wave Interferometer for Large Molecules. In: Physical Review Letters. Band 88, Nr. 10, 26. Februar 2002, S. 100404, doi:10.1103/PhysRevLett.88.100404.
- ↑ Stefan Gerlich, Sandra Eibenberger, Mathias Tomandl, Stefan Nimmrichter, Klaus Hornberger, Paul J. Fagan, Jens Tüxen, Marcel Mayor, Markus Arndt: Quantum interference of large organic molecules. In: Nature Communications 2, Article 263, doi:10.1038/ncomms1263
- ↑ Michael Springer: Welle oder Teilchen – ein Test mit dem Quantenradierer. In: Spektrum der Wissenschaft. Band 1. Spektrum der Wissenschaft Akademischer Verlag, 1996.